【牛客网刷题(数据结构)】:环形链表的约瑟夫问题

描述
编号为 1 到 n 的 n 个人围成一圈。从编号为 1 的人开始报数,报到 m 的人离开。
下一个人继续从 1 开始报数。
n-1 轮结束以后,只剩下一个人,问最后留下的这个人编号是多少?
O(n)
示例1
好环形链表的约瑟夫问题是一个经典的问题,它的描述如下:有n个人围成一圈,从第一个人开始报数,报到m的人出圈,剩下的人继续从1开始报数,直到剩下最后一个人。现在给定n和m,求最后剩下的人的编号
这个问题可以使用环形链表来解决。具体来说,我们可以先构建一个包含n个节点的环形链表,然后从第一个节点开始遍历链表,每次遍历m个节点,将第m个节点从链表中删除。重复这个过程直到链表中只剩下一个节点为止,这个节点就是最后剩下的节点
输入:
5,2
返回值:
3
说明:
开始5个人 1,2,3,4,5 ,从1开始报数,1->1,2->2编号为2的人离开
1,3,4,5,从3开始报数,3->1,4->2编号为4的人离开
1,3,5,从5开始报数,5->1,1->2编号为1的人离开
3,5,从3开始报数,3->1,5->2编号为5的人离开
最后留下人的编号是3
示例2
输入:
1,1
复制
返回值:
1
关于环形链表的约瑟夫问题,具体思路如下:
首先创建一个环形链表,链表中每个节点代表一个人,节点编号从1开始递增。
然后从第一个节点开始报数,每报到第m个人就将该节点从链表中删除。
删除节点后,从下一个节点重新开始报数,重复上述步骤,直到只剩下一个节点为止。
下面是C++代码实现:
#include <iostream>
using namespace std;struct ListNode {int val;ListNode* next;ListNode(int x) : val(x), next(NULL) {}
};int josephus(int n, int m) {ListNode* head = new ListNode(1);ListNode* cur = head;for (int i = 2; i <= n; i++) {cur->next = new ListNode(i);cur = cur->next;}cur->next = head; // 将链表首尾相连while (cur->next != cur) { // 只剩下一个节点时结束循环for (int i = 1; i < m; i++) {cur = cur->next;}ListNode* tmp = cur->next;cur->next = tmp->next;delete tmp;}int ans = cur->val;delete cur;return ans;
}int main() {int n, m;cin >> n >> m;cout << josephus(n, m) << endl;return 0;
}
C语言代码实现
#include <stdio.h>
#include <stdlib.h>// 定义链表节点结构体
typedef struct Node {int num; // 节点编号struct Node *next; // 指向下一个节点的指针
} Node;// 创建环形链表
Node *createList(int n) {Node *head = NULL, *tail = NULL;for (int i = 1; i <= n; i++) {Node *p = (Node *)malloc(sizeof(Node));p->num = i;if (head == NULL) {head = p;} else {tail->next = p;}tail = p;}tail->next = head; // 将尾节点指向头节点,形成环形链表return head;
}// 约瑟夫问题求解
void josephus(Node *head, int m) {Node *p = head, *prev = NULL;while (p->next != p) { // 只剩下一个节点时结束循环for (int i = 1; i < m; i++) {prev = p;p = p->next;}prev->next = p->next; // 删除节点printf("%d ", p->num);free(p);p = prev->next; // 从下一个节点重新开始报数}printf("%d\n", p->num);free(p);
}int main() {int n, m;printf("请输入总人数n和报数m:");scanf("%d%d", &n, &m);Node *head = createList(n);josephus(head, m);return 0;
}
相关文章:

【牛客网刷题(数据结构)】:环形链表的约瑟夫问题
描述 编号为 1 到 n 的 n 个人围成一圈。从编号为 1 的人开始报数,报到 m 的人离开。 下一个人继续从 1 开始报数。 n-1 轮结束以后,只剩下一个人,问最后留下的这个人编号是多少? O(n) 示例1 好环形链表的约瑟夫问题是一个经典的问…...
虾皮印尼买家号如何注册
虾皮(Shopee)是一个流行的电子商务平台,想要注册虾皮印尼买家号,可以按照以下步骤进行操作: 1、访问虾皮印尼站点:打开浏览器,输入虾皮印尼官网 2、点击"注册":在网站的…...

SpringBoot WebService服务端客户端使用教程
服务端: 依赖 <!-- webservice相关依赖--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web-services</artifactId></dependency><dependency><groupId&…...

【Python 千题 —— 基础篇】字符串长度
题目描述 题目描述 获取字符串长度是编程过程中常用的操作之一。编写一个程序,输入一个字符串,然后输出字符串的长度。 输入描述 输入一个字符串。 输出描述 程序将输入的字符串的长度输出。 代码讲解 下面是本题的代码: # 描述: 输…...

AIGC - 入门向量空间模型
文章目录 向量和向量空间向量的运算什么是向量空间?向量空间的几个重要概念向量之间的距离曼哈顿距离(Manhattan Distance)欧氏距离(Euclidean Distance)切比雪夫距离(Chebyshev Distance) 向量…...
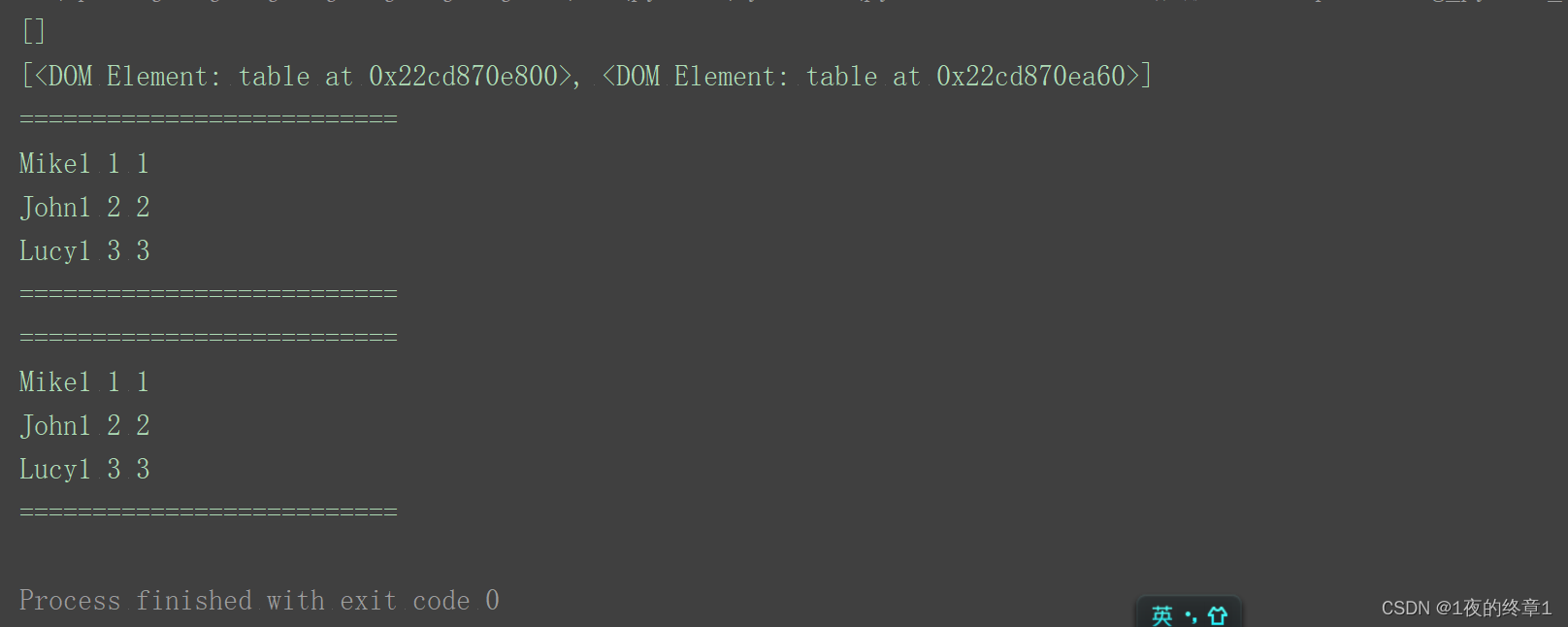
python中使用xml.dom.minidom模块读取解析xml文件
python中可以使用xml.dom.minidom模块读取解析xml文件 xml.dom.minidom模块应该是内置模块不用下载安装 对于一个xml文件来说比如这个xml文件的内容为如下 <excel version"1.0" author"huangzhihui"><table id"1"><colum id&qu…...

计算机网络第一章补充整理(计算机网络体系结构)
前言:以下整理内容,参考《计算机网络自顶向下》和哈工大的计网慕课 目录 计算机网络的体系结构的一些概念为什么采用分层结构?分层结构的优点分层结构的缺点 开放系统互连(OSI)参考模型物理层功能数据链路层功能网络层…...

2023_Spark_实验十七:导入招聘大数据(项目)
一、爬虫爬取的招聘网站数据 二、在MySQL中创建空表 SET FOREIGN_KEY_CHECKS0;-- ---------------------------- -- Table structure for jd_jobs -- ---------------------------- DROP TABLE IF EXISTS jd_jobs; CREATE TABLE jd_jobs (job_name text,job_date text,minSale…...

小程序无感刷新
下载wechat-http依赖 npm install wechat-http封装请求拦截器和相应拦截器,借助refreshToken实现无感刷新 // 导入 http 模块 import http from wechat-http // 基础路径,同时需添加合法请求域名 http.baseURL https://live-api.itheima.net // 配置请…...

Unity C#随笔:简述String和StringBuilder的区别
1.、String: 不可变性(Immutability): String对象一旦被创建,就不能被修改。每次对String对象进行操作时,实际上是创建了一个新的String对象,然后对象的引用重新指向这个新的对象。性能&#x…...
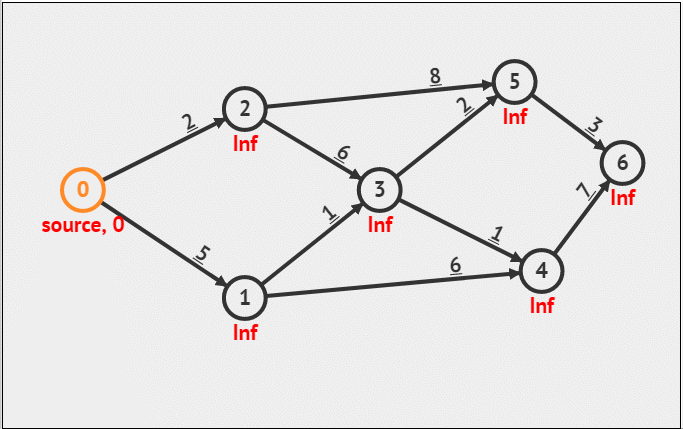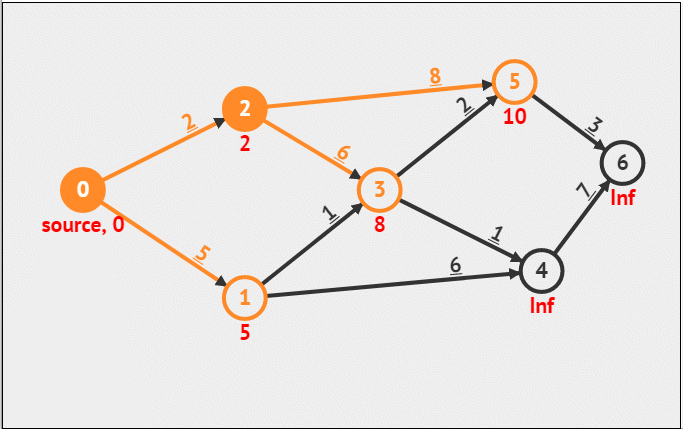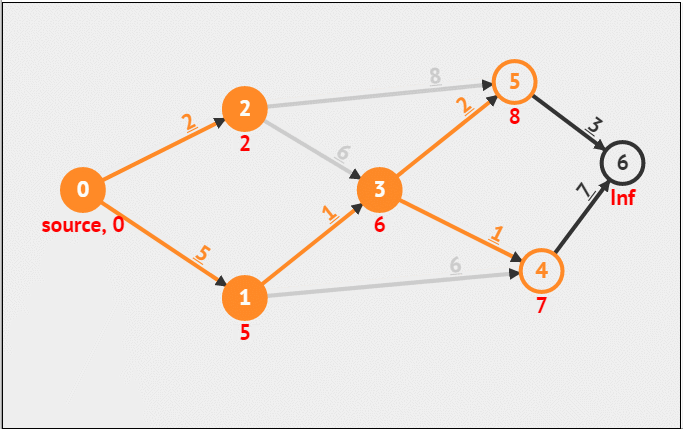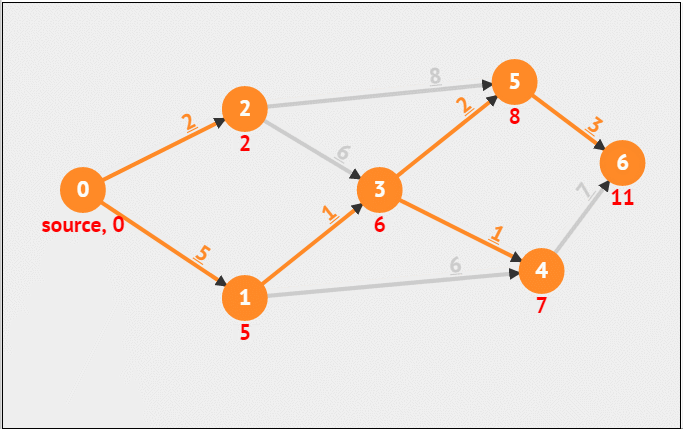
图论相关算法
一、迪杰斯特拉(Dijkstra)算法 迪杰斯特拉算法使用类似广度优先搜索的方法解决了带权图的单源最短路径问题。这是一个贪心算法。 1.核心思想 (1)每次选中一个点,这个点满足两个条件: 未被选过距离最短 (2…...

Python人工智能需要学什么
Python语言在人工智能开发领域有非常广泛的应用,随着人工智能平台的落地应用,未来采用Python语言来开发行业智能产品会是比较常见的选择。 然而进行人工智能开发仅凭Python语言是不够的,学习Python人工智能需要学习哪些知识呢? 一、Python…...

Java 获取请求真实IP
获取IP地址为 127.0.0.1, 或者内网地址 Nginx配置, 只有 proxy_pass 时只能获取到 127.0.0.1 location / {proxy_pass http://127.0.0.1:8080; }修改为 location / {#保留代理之前的host 包含客户端真实的域名和端口号proxy_set_header Host $host; #保留代理之前的真实客…...

Python突破浏览器TLS/JA3 指纹
JA3 是一种创建 SSL/TLS 客户端指纹的方法,一般一个网站的证书是不变的,所以浏览器指纹也是稳定的,能区分不同的客户端。 requests库 Python requests库请求一个带JA3指纹网站的结果: import requestsheaders {authority: tls…...

web安全之XSS攻击
什么是XSS攻击 XSS(Cross-Site Scripting)又称跨站脚本,XSS的重点不在于跨站点,而是在于脚本的执行。XSS是一种经常出现在 Web 应用程序中的计算机安全漏洞,是由于 Web 应用程序对用户的输入过滤不足而产生的。 常见…...
【技巧】如何设置Excel表只输入固定内容?
如果你需要在Excel表格中输入固定的内容,可以设置“限制录入内容”,这样就只能输入设置好的内容,避免不小心输入错误信息。下面来看看如何设置吧。 首先,打开Excel表格后,选中需要输入固定内容的表格区域。 比如图片…...

手机抬手亮屏解锁,用到了哪些硬件?
随着时代发展,智能手机以丰富的功能及便利性,成为了人们必不可少的物品,其中人脸解锁功能是非常有用的功能,广受年轻人的喜爱,那么你知道她是如何实现吗?今天凡小亿带你们探索! 手机抬手亮屏解锁…...

AI大模型高速发展,Web3还远吗?
在过去的几年里,人工智能(AI)和Web3技术都经历了令人瞩目的发展。AI大模型,特别是像GPT-3、GPT-4等这样的巨型语言模型,已经成为AI领域的明星,而Web3则代表了下一代互联网的愿景,具有去中心化和…...

CSS 滚动驱动动画 animation-range
animation-range 语法 normallength-percentagetimeline-range-name 具名时间线范围 named timeline rangecovercontainentry 和 entry-crossingexit 和 exit-crossing 兼容性 animation-range 这个属性可同时对 scroll progress timeline 和 view progress timeline 这两种不…...
快速学习MyBatisPlus
文章目录 前言一、条件构造器和常用接口1.wapper介绍2.QueryWrapper(1)组装查询条件(2)组装排序查询(3)组装删除查询(4)条件优先级(5)组装select子句…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
