AIGC - 入门向量空间模型
文章目录
- 向量和向量空间
- 向量的运算
- 什么是向量空间?
- 向量空间的几个重要概念
- 向量之间的距离
- 曼哈顿距离(Manhattan Distance)
- 欧氏距离(Euclidean Distance)
- 切比雪夫距离(Chebyshev Distance)
- 向量的长度
- 向量之间的夹角
- 余弦相似度
- 应用场景
- Code
- 向量空间模型
- 总结

向量和向量空间
-
标量(Scalar只是一个单独的数字,而且不能表示方向。从计算机数据结构的角度来看,标量就是编程中最基本的变量。
-
和标量对应的概念,就是线性代数中最常用、也最重要的概念,向量(Vector),也可以叫做矢量。它代表一组数字,并且这些数字是有序排列的。我们用数据结构的视角来看,向量可以用数组或者链表来表达。
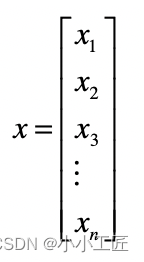
这里面的 n 就是向量的维
向量和标量最大的区别在于,向量除了拥有数值的大小,还拥有方向。向量或者矢量中的“向”和“矢”这两个字,都表明它们是有方向的。
为什么这一串数字能表示方向呢?
这是因为,如果我们把某个向量中的元素看作坐标轴上的坐标,那么这个向量就可以看作空间中的一个点。以原点为起点,以向量代表的点为终点,就能形成一条有向直线。而这样的处理其实已经给向量赋予了代数的含义,使得计算的过程中更加直观。
由于一个向量包含了很多个元素,因此我们自然地就可以把它运用在机器学习的领域。
由于特征有很多维,因此我们可以使用向量来表示某个物体的特征。其中,向量的每个元素就代表一维特征,而元素的值代表了相应特征的值,我们称这类向量为特征向量(Feature Vector)
向量的运算
标量和向量之间可以进行运算,比如标量和向量相加或者相乘时,我们直接把标量和向量中的每个元素相加或者相乘就行了.
可是,向量和向量之间的加法或乘法应该如何进行呢?
我们需要先定义向量空间。向量空间理论上的定义比较繁琐,不过二维或者三维的坐标空间可以很好地帮助你来理解。这些空间主要有几个特性:
- 空间由无穷多个的位置点组成;
- 这些点之间存在相对的关系;
- 可以在空间中定义任意两点之间的长度,以及任意两个向量之间的角度;
- 这个空间的点可以进行移动。
有了这些特点,我们就可以定义向量之间的加法、乘法(或点乘)、距离和夹角等等。
两个向量之间的加法,首先它们需要维度相同,然后是对应的元素相加。
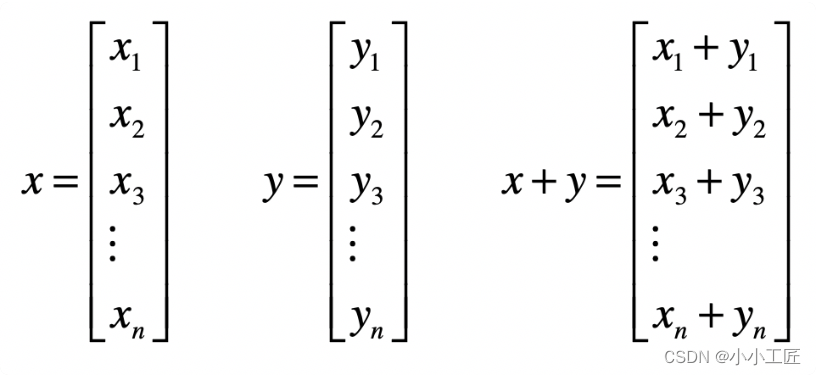
所以说,向量的加法实际上就是把几何问题转化成了代数问题,然后用代数的方法实现了几何的运算。下面画了一张图,来解释二维空间里,两个向量的相加,看完就能理解了。
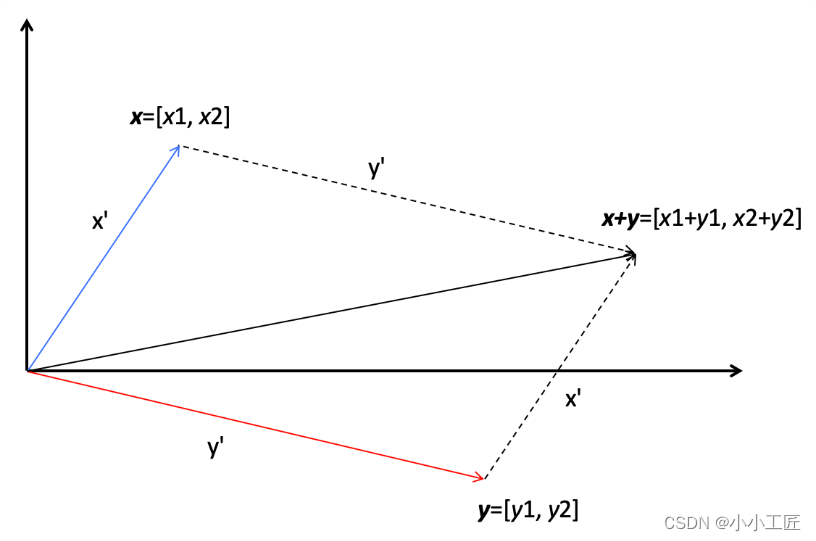
在这张图中,有两个向量 x 和 y,它们的长度分别是 x’和 y’,它们的相加结果是 x+y,这个结果所对应的点相当于 x 向量沿着 y 向量的方向移动 y’,或者是 y 向量沿着 x 向量的方向移动 x’
向量之间的乘法默认是点乘,向量 x 和 y 的点乘是这么定义的:
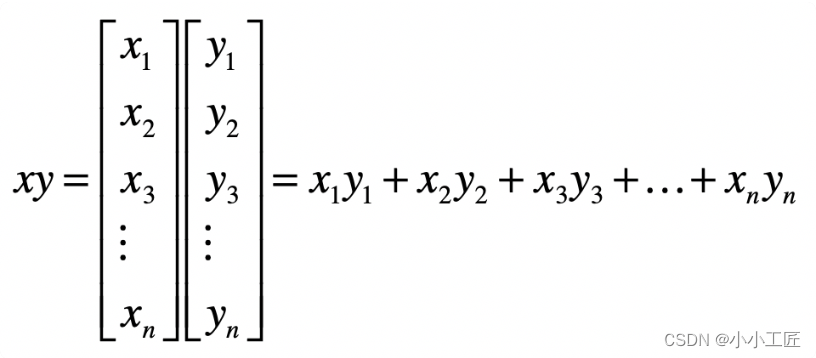
点乘的作用是把相乘的两个向量转换成了标量,它有具体的几何含义。我们会用点乘来计算向量的长度以及两个向量间的夹角,所以一般情况下我们会默认向量间的乘法是点乘。
至于向量之间的夹角和距离,它们在向量空间模型(Vector Space Model)中发挥了重要的作用。信息检索和机器学习等领域充分利用了向量空间模型,计算不同对象之间的相似程度
什么是向量空间?
首先假设有一个数的集合 F,它满足“F 中任意两个数的加减乘除法(除数不为零)的结果仍然在这个 F 中”,我们就可以称 F 为一个“域”。我们处理的数据通常都是实数,所以这里我只考虑实数域。而如果域 F 里的元素都为实数,那么 F 就是实数域。
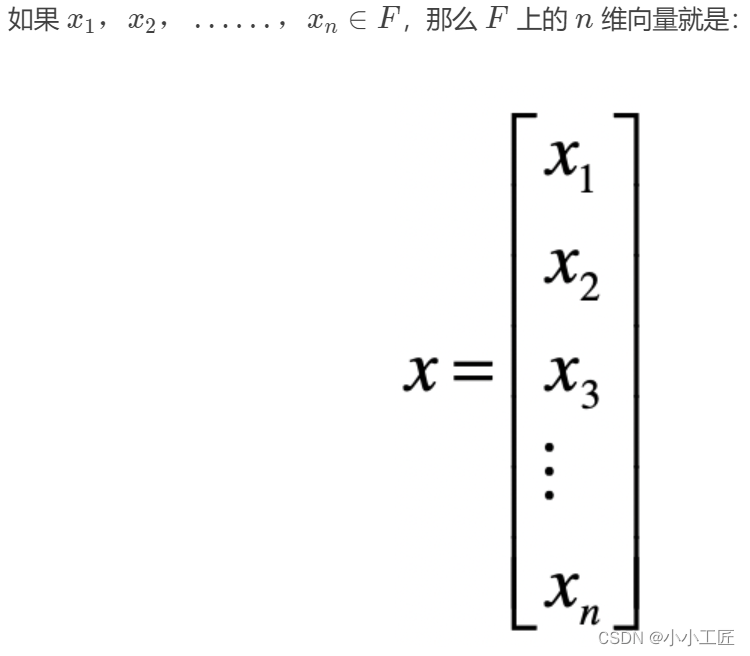
或者写成转置的形式:
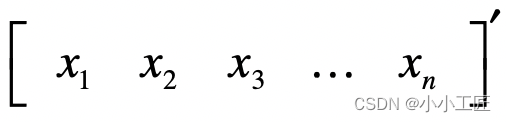
向量空间的几个重要概念
有了刚才的铺垫,接下来我们来看几个重要的概念:向量的长度、向量之间的距离和夹角。
向量之间的距离
有了向量空间,我们就可以定义向量之间的各种距离。我们之前说过,可以把一个向量想象为 n 维空间中的一个点。而向量空间中两个向量的距离,就是这两个向量所对应的点之间的距离。距离通常都是大于 0 的,这里介绍几种常用的距离,包括曼哈顿距离、欧氏距离、切比雪夫距离和闵可夫斯基距离。
曼哈顿距离(Manhattan Distance)
这个距离度量的名字由来非常有趣。你可以想象一下,在美国人口稠密的曼哈顿地区,从一个十字路口开车到另外一个十字路口,驾驶距离是多少呢?当然不是两点之间的直线距离,因为你无法穿越挡在其中的高楼大厦。你只能驾车绕过这些建筑物,实际的驾驶距离就叫作曼哈顿距离。由于这些建筑物的排列都是规整划一的,形成了一个个的街区,所以我们也可以形象地称它为“城市街区”距离。
这里画了张图方便理解这种距离。
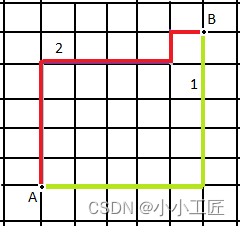
从图中可以看出,从 A 点到 B 点有多条路径,但是无论哪条,曼哈顿距离都是一样的。

欧氏距离(Euclidean Distance)

切比雪夫距离(Chebyshev Distance)



向量的长度
有了向量距离的定义,向量的长度就很容易理解了。向量的长度,也叫向量的模,是向量所对应的点到空间原点的距离。通常我们使用欧氏距离来表示向量的长度。

向量之间的夹角

余弦相似度
余弦相似度是一种用于衡量两个向量之间相似性的度量方法,通常用于文本挖掘、信息检索和自然语言处理等领域。它通过计算两个向量之间的夹角余弦值来衡量它们在多维空间中的方向相似性。余弦相似度通常用于比较两个文本文档之间的相似性,或者用于向量空间模型中的相关性分析。
余弦相似度的计算公式如下:
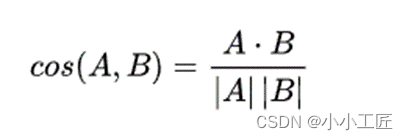
余弦相似度的取值范围在 -1 到 1 之间。
- 如果余弦相似度接近 1,表示两个向量非常相似,它们的方向几乎一致;
- 如果余弦相似度接近 -1,表示两个向量方向完全相反;
- 如果余弦相似度接近 0,表示两个向量之间几乎没有方向相似性。
在自然语言处理中,可以使用余弦相似度来衡量文档之间的相似性,或者在信息检索中用于排序搜索结果,以便找到与查询最相关的文档。
应用场景
-
文本相似度:
假设有两个文本文档,分别是 “机器学习是人工智能的一部分” 和 “深度学习是AI领域的一个分支”。我们可以将这两个文档表示为词频向量,其中每个维度代表一个词汇,值表示该词汇在文档中的频率。然后,可以使用余弦相似度来比较这两个文档的相似性。如果它们在使用的词汇上有很多重叠,余弦相似度将接近1,表示它们非常相似。
-
用户兴趣:
想象一个在线商店,有两个用户,分别在网站上浏览过的商品类别如下:用户A看了电子产品和家居用品,而用户B看了电子产品和厨房用具。可以将每个用户的兴趣表示为一个向量,其中每个维度代表一个商品类别,值表示用户对该类别的兴趣程度。然后,通过余弦相似度来比较两个用户的兴趣向量。如果它们在感兴趣的商品类别上有很多重叠,余弦相似度将接近1,表示这两个用户的兴趣相似。
-
图像相似度:
在计算机视觉中,余弦相似度也可以用于比较图像。如果两张图像表示为像素值的向量,余弦相似度可以用来衡量它们的结构和颜色的相似性。两张相似的图像的余弦相似度将接近1,而完全不同的图像余弦相似度将接近0。
这些例子说明了余弦相似度的概念,即在多维空间中,两个向量的方向越接近,余弦相似度越高,表示它们越相似。这种相似性度量在各种应用中都非常有用,从文本和用户兴趣分析到图像和推荐系统。
Code
import java.util.Arrays;public class CosineSimilarity {public static void main(String[] args) {// 两个文本文档 0.44474958999666075
// String text1 = "机器学习是人工智能的一部分";
// String text2 = "深度学习是AI领域的一个分支";// 两个文本文档 0.9999999999999998
// String text1 = "我是小工匠";
// String text2 = "小工匠是我";// 两个文本文档 0.687922956942992String text1 = "RAG 一直在自然语言处理(NLP) 领域掀起波澜。RAG 的核心是一个混合框架,它集成了检索模型和生成模型,生成的文本不仅上下文准确,而且信息丰富。";String text2 = "RAG(Retrieval-Augmented Generation)是一项引人注目的技术,已经引发了自然语言处理(NLP)领域的广泛关注。它的核心思想是将检索模型和生成模型相融合,使得生成的文本不仅具有准确的上下文信息,而且内容丰富多彩";// 将文本分割成单词String[] words1 = text1.split("");String[] words2 = text2.split("");// 创建词汇表String[] vocabulary = getVocabulary(words1, words2);// 将文本转换为词频向量int[] vector1 = getVector(words1, vocabulary);int[] vector2 = getVector(words2, vocabulary);// 计算余弦相似度double cosineSimilarity = calculateCosineSimilarity(vector1, vector2);System.out.println("余弦相似度: " + cosineSimilarity);}// 创建词汇表public static String[] getVocabulary(String[] words1, String[] words2) {String[] vocabulary = Arrays.copyOf(words1, words1.length);for (String word : words2) {if (!Arrays.asList(vocabulary).contains(word)) {vocabulary = Arrays.copyOf(vocabulary, vocabulary.length + 1);vocabulary[vocabulary.length - 1] = word;}}return vocabulary;}// 将文本转换为词频向量public static int[] getVector(String[] words, String[] vocabulary) {int[] vector = new int[vocabulary.length];Arrays.fill(vector, 0);for (String word : words) {for (int i = 0; i < vocabulary.length; i++) {if (word.equals(vocabulary[i])) {vector[i]++;}}}return vector;}// 计算余弦相似度public static double calculateCosineSimilarity(int[] vector1, int[] vector2) {double dotProduct = 0;double magnitude1 = 0;double magnitude2 = 0;for (int i = 0; i < vector1.length; i++) {dotProduct += vector1[i] * vector2[i];magnitude1 += Math.pow(vector1[i], 2);magnitude2 += Math.pow(vector2[i], 2);}magnitude1 = Math.sqrt(magnitude1);magnitude2 = Math.sqrt(magnitude2);return dotProduct / (magnitude1 * magnitude2);}
}
向量空间模型
理解了向量间距离和夹角余弦这两个概念,再来看向量空间模型(Vector Space Model)就不难了。
向量空间模型假设所有的对象都可以转化为向量,然后使用向量间的距离(通常是欧氏距离)或者是向量间的夹角余弦来表示两个对象之间的相似程度。
使用下图来展示空间中向量之间的距离和夹角。
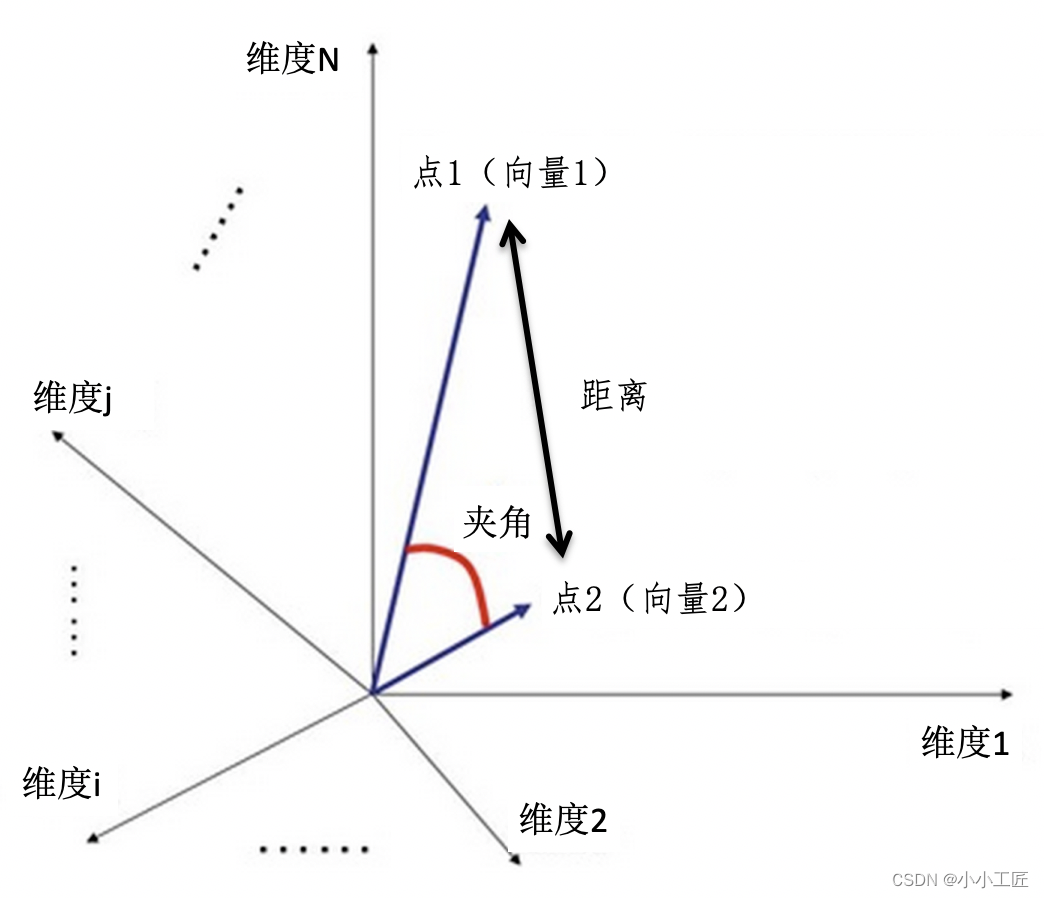
由于夹角余弦的取值范围已经在 -1 到 1 之间,而且越大表示越相似,所以可以直接作为相似度的取值。相对于夹角余弦,欧氏距离 ED 的取值范围可能很大,而且和相似度呈现反比关系,所以通常要进行 1/(ED+1) 这种归一化。
当 ED 为 0 的时候,变化后的值就是 1,表示相似度为 1,完全相同。当 ED 趋向于无穷大的时候,变化后的值就是 0,表示相似度为 0,完全不同。所以,这个变化后的值,取值范围是 0 到 1 之间,而且和相似度呈现正比关系。
早在上世纪的 70 年代,人们把向量空间模型运用于信息检索领域。由于向量空间可以很形象地表示数据点之间的相似程度,因此现在我们也常常把这个模型运用在基于相似度的一些机器学习算法中,例如 K 近邻(KNN)分类、K 均值(K-Means)聚类等等。
总结
为了让计算机理解现实世界中的事物,我们会把事物的特点转换成为数据,并使用多维度的特征来表示某个具体的对象。多个维度的特征很容易构成向量,因此我们就可以充分利用向量和向量空间,来刻画事物以及它们之间的关系。
我们可以在向量空间中定义多种类型的向量长度和向量间距离,用于衡量向量之间的差异或者说相似程度。此外,夹角余弦也是常用的相似度衡量指标。和距离相比,夹角余弦的取值已经控制在[-1, 1]的范围内,不会因为异常点所产生的过大距离而受到干扰。
向量空间模型充分利用了空间中向量的距离和夹角特性,来描述文档和查询之间的相似程度,或者说相关性。虽然向量空间模型来自信息检索领域,但是也被广泛运用在机器学习领域中。

相关文章:

AIGC - 入门向量空间模型
文章目录 向量和向量空间向量的运算什么是向量空间?向量空间的几个重要概念向量之间的距离曼哈顿距离(Manhattan Distance)欧氏距离(Euclidean Distance)切比雪夫距离(Chebyshev Distance) 向量…...
python中使用xml.dom.minidom模块读取解析xml文件
python中可以使用xml.dom.minidom模块读取解析xml文件 xml.dom.minidom模块应该是内置模块不用下载安装 对于一个xml文件来说比如这个xml文件的内容为如下 <excel version"1.0" author"huangzhihui"><table id"1"><colum id&qu…...

计算机网络第一章补充整理(计算机网络体系结构)
前言:以下整理内容,参考《计算机网络自顶向下》和哈工大的计网慕课 目录 计算机网络的体系结构的一些概念为什么采用分层结构?分层结构的优点分层结构的缺点 开放系统互连(OSI)参考模型物理层功能数据链路层功能网络层…...

2023_Spark_实验十七:导入招聘大数据(项目)
一、爬虫爬取的招聘网站数据 二、在MySQL中创建空表 SET FOREIGN_KEY_CHECKS0;-- ---------------------------- -- Table structure for jd_jobs -- ---------------------------- DROP TABLE IF EXISTS jd_jobs; CREATE TABLE jd_jobs (job_name text,job_date text,minSale…...

小程序无感刷新
下载wechat-http依赖 npm install wechat-http封装请求拦截器和相应拦截器,借助refreshToken实现无感刷新 // 导入 http 模块 import http from wechat-http // 基础路径,同时需添加合法请求域名 http.baseURL https://live-api.itheima.net // 配置请…...

Unity C#随笔:简述String和StringBuilder的区别
1.、String: 不可变性(Immutability): String对象一旦被创建,就不能被修改。每次对String对象进行操作时,实际上是创建了一个新的String对象,然后对象的引用重新指向这个新的对象。性能&#x…...
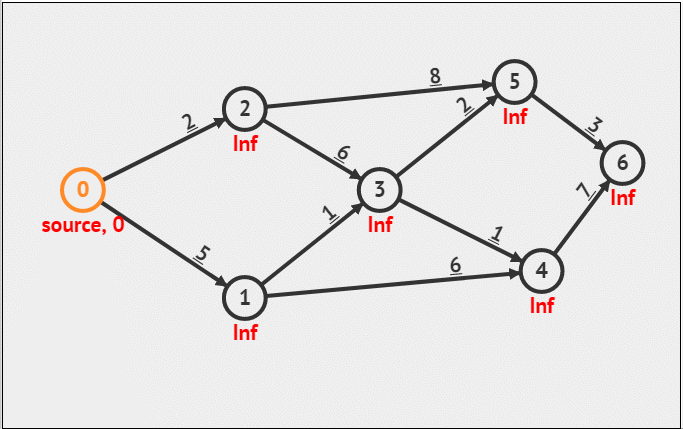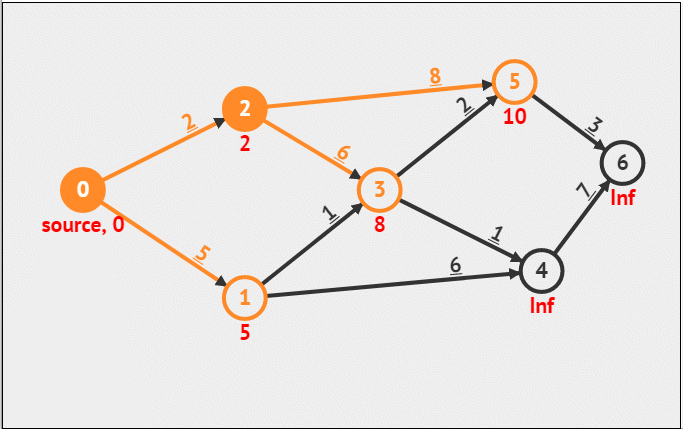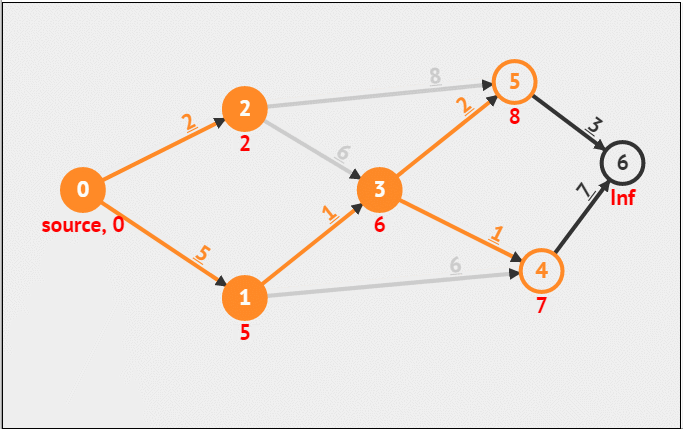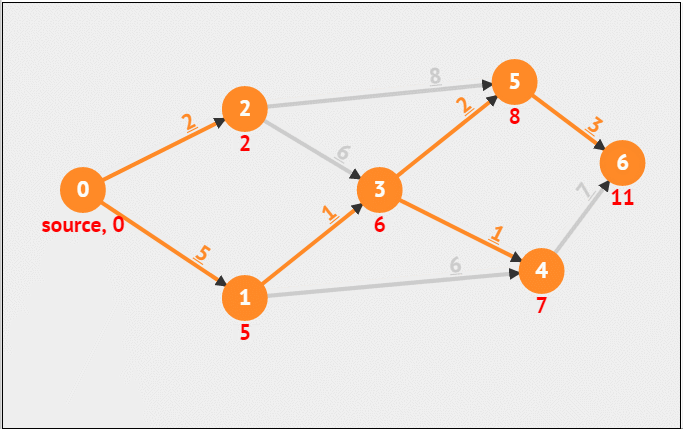
图论相关算法
一、迪杰斯特拉(Dijkstra)算法 迪杰斯特拉算法使用类似广度优先搜索的方法解决了带权图的单源最短路径问题。这是一个贪心算法。 1.核心思想 (1)每次选中一个点,这个点满足两个条件: 未被选过距离最短 (2…...

Python人工智能需要学什么
Python语言在人工智能开发领域有非常广泛的应用,随着人工智能平台的落地应用,未来采用Python语言来开发行业智能产品会是比较常见的选择。 然而进行人工智能开发仅凭Python语言是不够的,学习Python人工智能需要学习哪些知识呢? 一、Python…...

Java 获取请求真实IP
获取IP地址为 127.0.0.1, 或者内网地址 Nginx配置, 只有 proxy_pass 时只能获取到 127.0.0.1 location / {proxy_pass http://127.0.0.1:8080; }修改为 location / {#保留代理之前的host 包含客户端真实的域名和端口号proxy_set_header Host $host; #保留代理之前的真实客…...

Python突破浏览器TLS/JA3 指纹
JA3 是一种创建 SSL/TLS 客户端指纹的方法,一般一个网站的证书是不变的,所以浏览器指纹也是稳定的,能区分不同的客户端。 requests库 Python requests库请求一个带JA3指纹网站的结果: import requestsheaders {authority: tls…...

web安全之XSS攻击
什么是XSS攻击 XSS(Cross-Site Scripting)又称跨站脚本,XSS的重点不在于跨站点,而是在于脚本的执行。XSS是一种经常出现在 Web 应用程序中的计算机安全漏洞,是由于 Web 应用程序对用户的输入过滤不足而产生的。 常见…...
【技巧】如何设置Excel表只输入固定内容?
如果你需要在Excel表格中输入固定的内容,可以设置“限制录入内容”,这样就只能输入设置好的内容,避免不小心输入错误信息。下面来看看如何设置吧。 首先,打开Excel表格后,选中需要输入固定内容的表格区域。 比如图片…...

手机抬手亮屏解锁,用到了哪些硬件?
随着时代发展,智能手机以丰富的功能及便利性,成为了人们必不可少的物品,其中人脸解锁功能是非常有用的功能,广受年轻人的喜爱,那么你知道她是如何实现吗?今天凡小亿带你们探索! 手机抬手亮屏解锁…...

AI大模型高速发展,Web3还远吗?
在过去的几年里,人工智能(AI)和Web3技术都经历了令人瞩目的发展。AI大模型,特别是像GPT-3、GPT-4等这样的巨型语言模型,已经成为AI领域的明星,而Web3则代表了下一代互联网的愿景,具有去中心化和…...

CSS 滚动驱动动画 animation-range
animation-range 语法 normallength-percentagetimeline-range-name 具名时间线范围 named timeline rangecovercontainentry 和 entry-crossingexit 和 exit-crossing 兼容性 animation-range 这个属性可同时对 scroll progress timeline 和 view progress timeline 这两种不…...
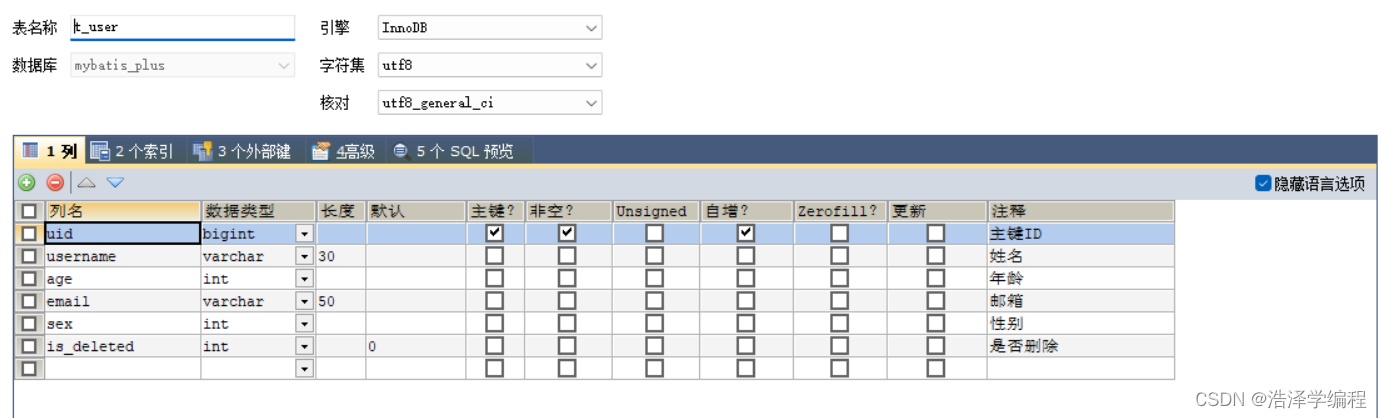
快速学习MyBatisPlus
文章目录 前言一、条件构造器和常用接口1.wapper介绍2.QueryWrapper(1)组装查询条件(2)组装排序查询(3)组装删除查询(4)条件优先级(5)组装select子句…...
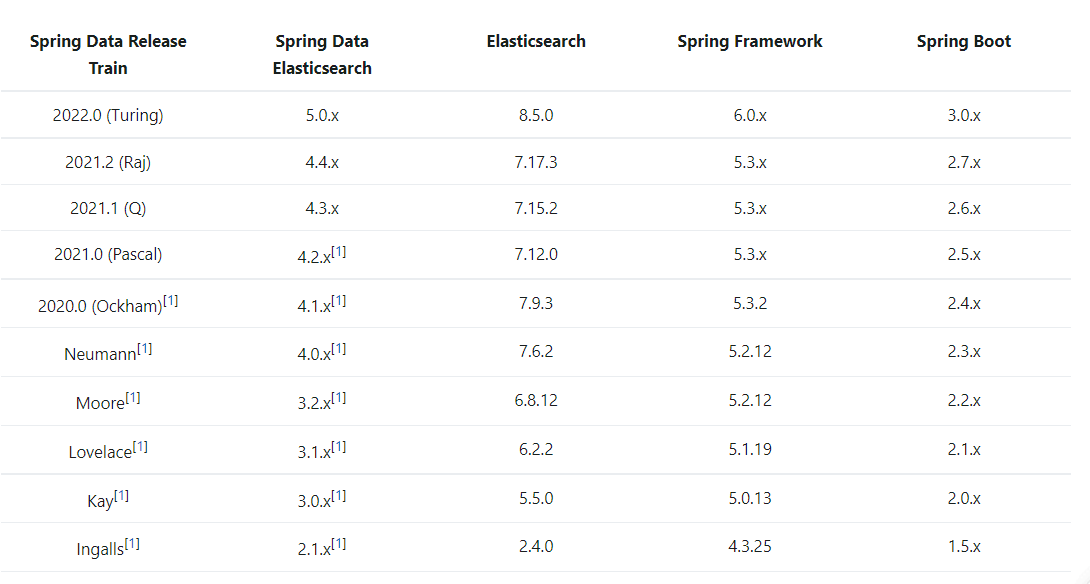
ElasticsearchRestTemplate 和ElasticsearchRepository 的使用
目录 一、使用ElasticsearchRestTemplate类 1.引用Maven类库 2. 配置文件application.yml 3.创建实体类(用于JSON文档对象的转换) 二、使用ElasticsearchRepository 类 1.引用Maven类库 2. 配置文件application.yml 3. ElasticsearchRepository接…...
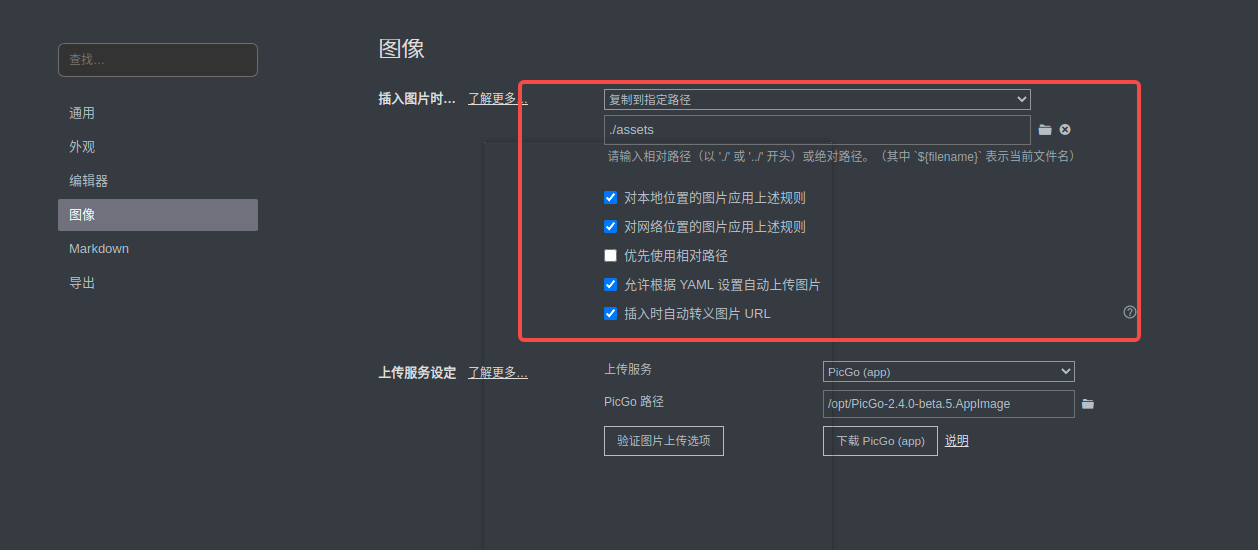
Typora +Picgo 搭建个人笔记
文章目录 Typora Picgo 搭建个人笔记一、Picgo Github 搭建图床1.基础设置2. 将配置导出,方便下次使用 二、Typora:设置 :1. 基本设置2. 导出自动提交3. 备份图片 Typora Picgo 搭建个人笔记 typora 下载地址: https://zahui.fan…...

八、K8S之HPA自动扩缩容
HPA 一、概念 HPA(Horizontal Pod Autoscaler,水平 Pod 自动伸缩)是 Kubernetes 中的一种特性,其作用是根据资源使用情况自动调整 Pod 的副本数,以实现应用程序的自动扩展和收缩。 HPA 可以根据 CPU 使用率或其他自…...

损失函数总结(二):L1Loss、MSELoss
损失函数总结(二):L1Loss、MSELoss 1 引言2 损失函数2.1 L1Loss2.2 MSELoss 3 总结 1 引言 在上一篇博文中介绍了损失函数是什么以及为什么使用损失函数,从这一篇博文就开始关于损失函数有哪些进行进一步的介绍。这里放一张损失函…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
