HyperLogLog算法
前言
现在很多站点基本都有统计 PV 和 UV 的需求,PV 的统计很简单,在 Redis 里面维护一个计数器,页面每访问一次计数器就 +1,获取 PV 就是读取计数器的值。
相比之下,UV 的统计就比较麻烦了,因为要对用户去重,UV 统计其实就是基数统计,最简单的做法就是记录下集合中所有不重复的元素。
比如,你可以用 Set 来统计,Set 不会存储重复的元素,用户每次访问都把 UserID 写入 Set 集合,最终调用 SCARD 命令获取集合元素数量即可。
> sadd uv 1001 1002 1003
(integer) 3
> scard uv
(integer) 3
使用 Set 的缺点是太耗内存了,假设 UserID 是 Long 类型,占用 8 字节,Set 底层用哈希表存储,Key 是 UserID,Value 是空值,但是指针本身还是会消耗 8 字节,即一个 Entry 占用 16 字节,存储一亿个 UserID 大约占用 1.49G。
或者,你还可以用 BitMap 来统计。哪个用户访问了页面,就把 UserID 对应的位设为 1,最后统计 1 的数量即可。假设有一亿个用户,就需要一亿个 Bit,大约 12MB,相比 Set 确实节省了很多内存,但是仍然不够省,假设有一千个页面需要统计,就需要消耗约 12GB 的空间。
无论是 Set 还是 BitMap 实现,它们都直接或间接的存储了元素,这种方式带来的问题是:占用的内存空间会随着统计的数据量线性增长。
在统计学里还有一种基于概率的统计算法,它不存储元素本身,所以极其节省内存,但它牺牲的是准确率。HyperLogLog 就是一种基于概率的统计算法,它仅需少量的内存空间,就可以统计超大规模的数据量,在不追求绝对准确的场景下,更推荐使用这种算法。
HyperLogLog
Redis 提供了 HyperLogLog 数据类型,使用极其简单,PFADD 命令把值写入到 HyperLogLog;PFCOUNT 命令对 HyperLogLog 做基数估算。
> pfadd uv 1001 1002 1003
(integer) 1
> pfcount uv
(integer) 3
确实可以实现我们的需求,你查阅文档发现每个 HyperLogLog 仅仅占用 12KB,就可以统计 2^64 个基数,而且误差率基本在0.81%,这效率高的离谱啊,怎么做到的呢?
最大似然估计
HyperLogLog 只有 12KB 的空间,它打死也存不下2^64个元素,所以你是无法奢求它能做到精确统计的。换言之,HyperLogLog 本身并不存储元素,它只存储元素极端值的特点,然后对基数做估算。
这里面涉及到一个数学原理:最大似然估计(MLE)
最大似然估计(maximum likelihood estimation)是一种重要而普遍的求估计量的方法。最大似然法明确地使用概率模型,其目标是寻找能够以较高概率产生观察数据的系统发生树。最大似然法是一类完全基于统计的系统发生树重建方法的代表。
通俗的理解就是,利用已知的样本数据,来反推出可能性最高的模型参数。
举个例子,现在有一个黑盒,里面放了 M 数量的白球,N 数量的黑球。你现在每次从黑盒里取出一个球记录下颜色再放回去,反复取 100 次,结果是 99 次白球,1 次黑球。由此我们可以推理出,黑盒里极有可能放了 99 个白球,1 个黑球。这个推算结果可能并不准确,但是我们认为它的误差率是最小的。
伯努利实验
伯努利试验是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是试验只有两种可能结果:成功或者失败。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努利概型。单个伯努利试验是没有多大意义的,然而,当我们反复进行伯努利试验,去观察这些试验有多少是成功的,多少是失败的,事情就变得有意义了,这些累计记录包含了很多潜在的非常有用的信息。
比如最简单的抛硬币过程就可以看作是一次伯努利实验,抛硬币的结果只有两种:正面朝上或反面朝上,且两种结果的概率都是 50%。
我们假设正面是成功,反面是失败,每抛到一次正面记为一次完整的试验,同时记录下所有试验里抛硬币最多的次数。试验次数记为 N,最大抛硬币次数记为 K。如下示例:
N=1 反反正 K=3
N=2 反反反正 K=4
现在我告诉你我一共进行了 N 次试验,最多一次抛了 4 次才抛到正面朝上,即 K=4,现在请你推理出 N 的数量。
我们来试着分析一下这个问题,首先我们能拿到的信息就只有 K=4,即最多的一次抛出了反反反正的结果。可能运气很好第一次就抛到了,也可能运气很背,抛了很多次才得到这个结果。具体试验了多少次我们不得而知,我们只能依靠 K=4 这个结果发生的概率去反推试验次数。
反反反正是 4 次独立的抛硬币结果,第一次反的概率是 0.5,第二次还是反的概率是0.5 * 0.5=0.25,以此类推,抛出这个结果的概率是1/16,即1/2^k,所以我们可以估算出大概率进行了 16 次试验。
发现了吗?我们仅凭一个 K=4 就可以估算出 N,虽然结果可能不准确,但确实得到了一个结果,接下来就是解决误差率的问题了。这也正是 HyperLogLog 的核心原理,它不保存每次试验的结果,它只保留 K,所以极其节省空间,最后依靠 K 来估算 N。
探寻KN的关系
基于以上理论,我们发现可以通过 K 值估算 N 值,只是估算的结果误差比较大,我们来探寻一下 KN 的关系,一步步的解决误差率,最终得到一个比较稳定和准确的 HyperLogLog 算法。
简单估算
先看一个最简单的 V1 版本,直接模拟上文中的抛硬币,记录下最大值 K,然后估算 N。
public class KN1 {int k;final int n;public KN1(int n) {this.n = n;}void test() {int counter = 1;for (int i = 0; i < n; i++) {if (nextBoolean()) {// 随机到true 代表正面,记录下最大K值if (counter > k) {k = counter;}counter = 1;} else {counter++;}}// 估算n=2的k次方long estimate = Math.round(Math.pow(2, k));DecimalFormat decimalFormat = new DecimalFormat("0.0000%");double error = Math.abs(n - estimate) / (double) n;System.err.printf("%-10s %-10s %-10s\n", n, estimate, decimalFormat.format(error));}boolean nextBoolean() {return ThreadLocalRandom.current().nextBoolean();}public static void main(String[] args) {System.err.printf("%-10s %-10s %-10s\n", "实际n", "预估n", "误差率");for (int i = 0; i <= 10000000; ) {if (i < 10) {i++;} else {i *= 10;}new KN1(i).test();}}
}
结果输出:
实际n 预估n 误差率
1 2 100.0000%
2 2 0.0000%
3 4 33.3333%
4 2 50.0000%
5 4 20.0000%
6 1 83.3333%
7 8 14.2857%
8 16 100.0000%
9 8 11.1111%
10 64 540.0000%
100 64 36.0000%
1000 1024 2.4000%
10000 16384 63.8400%
100000 262144 162.1440%
1000000 262144 73.7856%
10000000 16777216 67.7722%
100000000 33554432 66.4456%
观察结果发现,这种简单粗暴的估算,误差率非常高,肯定不是一个可用的版本,但是我们可以获得两个信息:
- K N 确实存在指数关系,至少估算的误差没有超出一个数量级,证明思路是对的
- 数据规模越小,误差率往往越大
分桶平均
思路是对的,接下来就是解决误差率的问题了。
怎么减小估算的误差呢?如果大家做过试验,应该就能想到,如果一次试验的误差率较大,那么就多做几轮试验,然后求平均值,这样就可以减小单次试验结果对最终结果的影响。
于是我们初始化 16384 个桶,每做完一次试验,就把 K 值随机写入一个桶(只保留最大K值),然后对每个桶的 K 求平均值,最终再基于 K 平均值估算 N。于是我们得到算法的 V2 版本:
public class KN2 {final int m;// 桶数量final int n;final int[] buckets;public KN2(int n) {this.m = 16384;this.n = n;this.buckets = new int[m];}void test() {int counter = 1;for (int i = 0; i < n; i++) {if (nextBoolean()) {// 把K值随机写入一个桶int index = nextBucket();if (counter > buckets[index]) {buckets[index] = counter;}counter = 1;} else {counter++;}}count();}private void count() {double sum = 0.0;int validBuckets = 0;for (int bucket : buckets) {if (bucket > 0) {// 过滤空桶sum += bucket;validBuckets++;}}// 估算的每个桶的平均值double avg = Math.pow(2, sum / validBuckets);// 估算值 = 均值*桶数量long estimate = Math.round(avg * validBuckets);DecimalFormat decimalFormat = new DecimalFormat("0.0000%");double error = Math.abs(n - estimate) / (double) n;System.err.printf("%-10s %-10s %-10s\n", n, estimate, decimalFormat.format(error));}boolean nextBoolean() {return ThreadLocalRandom.current().nextBoolean();}int nextBucket() {return ThreadLocalRandom.current().nextInt(m);}
}
结果输出:
实际n 预估n 误差率
1 2 100.0000%
2 2 0.0000%
3 2 33.3333%
4 4 0.0000%
5 4 20.0000%
6 16 166.6667%
7 11 57.1429%
8 13 62.5000%
9 16 77.7778%
10 16 60.0000%
100 222 122.0000%
1000 2016 101.6000%
10000 18362 83.6200%
100000 134363 34.3630%
1000000 1257570 25.7570%
10000000 12302338 23.0234%
100000000 124887784 24.8878%
观察结果发现,经过分桶平均后,误差率确实减小了,在数据规模比较大的情况下,误差率基本控制在20%~30%,但它仍然不是一个可用版本。
调和平均
分桶平均以后,误差率确实小了,但是还不够小。因为算数平均数有一个缺点,就是结果容易受到大值的影响,使得结果偏离整体数据的中心位置。
举个例子,小王的月薪是3000元,小李的月薪是30000元,他俩平均月薪是16500元。在小王看来这个数据就很扯蛋,自己什么时候工资这么高了,这就是算数平均数导致的,因为它的结果容易收到大值的影响。反观调和平均数,它会偏向于集合里的小数。
调和平均数:又称倒数平均数,它先对集合内的每个数求倒数,然后把所有的倒数相加得到 sum,最后用集合里的元素数量除以 sum 就可以得到调和平均数。
H = n 1 x 1 + 1 x 2 + . . . + 1 x n = n ∑ i = 1 n 1 x i H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n}} = \frac{n}{\sum_{i=1}^n \frac{1}{x_i}} H=x11+x21+...+xn1n=∑i=1nxi1n
我们用调和平均数重新计算一下小王和小李的平均薪资,avg = 2/(1/3000+1/30000)结果约为 5455 元,这个数据在小王看来还是比较靠谱的。
基于以上理论,我们可以把算数平均数换成调和平均数,以此来进一步降低结果误差。于是我们得到算法的 V3 版本:
public class KN3 {final int m;final int n;final int[] buckets;public KN3(int n) {this.m = 16384;this.n = n;this.buckets = new int[m];}void test() {int counter = 1;for (int i = 0; i < n; i++) {if (nextBoolean()) {int index = nextBucket();if (counter > buckets[index]) {buckets[index] = counter;}counter = 1;} else {counter++;}}count();}private void count() {double sum = 0.0;int validBuckets = 0;for (int bucket : buckets) {if (bucket > 0) {sum += 1.0 / bucket; // 倒数相加 求调和平均数validBuckets++;}}// 每个桶的平均数double avg = Math.pow(2, validBuckets / sum);// 总的估算值long estimate = Math.round(avg * validBuckets);DecimalFormat decimalFormat = new DecimalFormat("0.0000%");double error = Math.abs(n - estimate) / (double) n;System.err.printf("%-10s %-10s %-10s\n", n, estimate, decimalFormat.format(error));}boolean nextBoolean() {return ThreadLocalRandom.current().nextBoolean();}int nextBucket() {return ThreadLocalRandom.current().nextInt(m);}
}
结果输出:
实际n 预估n 误差率
1 2 100.0000%
2 0 100.0000%
3 4 33.3333%
4 7 75.0000%
5 5 0.0000%
6 8 33.3333%
7 11 57.1429%
8 5 37.5000%
9 16 77.7778%
10 15 50.0000%
100 142 42.0000%
1000 1325 32.5000%
10000 12229 22.2900%
100000 72504 27.4960%
1000000 888320 11.1680%
10000000 10116344 1.1634%
100000000 105180060 5.1801%
观察结果发现,使用调和平均数后,误差率进一步降低了,在数据规模较大时,误差率可以控制在10%以内。但是它仍然不是一个可用的版本,主要原因有:
- 数据规模较小时,误差率还是很大
- 整体误差率还是不够小,还能不能再精确一点
HyperLogLog实现
探寻 K N 的关系,我们迭代了算法的三个版本,估算结果的误差率逐步降低,其实 V3 的算法已经很接近 HyperLogLog 了,相较于 V3,HyperLogLog 的特点主要有:
- 仍然采用 调和平均数 计算
- 数据规模较小/超大时,对结果进行过修正(解决 V3 的问题)
- 引入 constant 修正常数(进一步降低误差率)
接下来,我们就用 Java 实现一个简单的 HyperLogLog 算法,看看它比 V3 的误差率又能提升多少呢?
问题:怎么把输入的元素转换成上述抛硬币的过程???
对输入的元素做哈希运算,得到哈希值。把哈希值的每个二进制位看做是一次抛硬币的结果,0代表反面,1代表正面。从低位开始数,直到第一个出现 1 的位,把经过的位数记为 K 值。
问题:HyperLogLog 如何对估算结果修正???
HyperLogLog 采用分段偏差修正,当数据规模太小/太大时,都有专门的修正算法,针对一般规模的数据会在最终结果上乘以一个修正常数 constant。
假设 E 为估算结果,分段偏差修正算法如下:
- 当 E ≤ 5 2 m E \leq \frac{5}{2}m E≤25m时,数据规模太小
E = m ∗ l o g m / V E=m*log^{m/V} E=m∗logm/V V = 空桶数量
- 当 5 2 m < E ≤ 1 30 2 32 \frac{5}{2}m < E \leq \frac{1}{30}2^{32} 25m<E≤301232时,数据规模一般直接用 HyperLogLog 公式
E = c o n s t ∗ m ∗ m ∑ i = 1 m 1 2 R i E = const*m*\frac{m}{\sum_{i=1}^m \frac{1}{2^Ri}} E=const∗m∗∑i=1m2Ri1m
- 当 E > 1 30 2 32 E > \frac{1}{30}2^{32} E>301232时,数据规模太大
E = − 2 32 l o g ( 1 − E / 2 32 ) E=-2^{32}log(1-E/2^{32}) E=−232log(1−E/232)
修正常数 constant 是根据分桶数量决定的:
double getConstant(int buckets) {switch (buckets) {case 16:return 0.673;case 32:return 0.697;case 64:return 0.709;default:return (0.7213 / (1 + 1.079 / buckets));}
}
实现思路:
- 初始化 16384 个桶,用来做分桶平均
- 对元素做哈希运算,得到 64 位长整型哈希值 hash
- 取 hash 的低 14 位值,用作分桶索引号
- 取 hash 的高 50 位值,计算前导0的数量(从低位开始连续0的数量)lowBits
- 把 lowBits 写入到桶
- 最后先估算每个桶的 N 值,再求调和平均数,最终估算 N 值
基于这个思路,最终我们用 Java 实现的一个简版 HyperLogLog 就出来了:
public class HyperLogLog {// 定位桶的比特数 低14位private static final int BUCKET_BITS = 14;private final int m;// 桶数量private final byte[] buckets; // 桶private final double constant; // 修正常数 根据桶数量设置public HyperLogLog() {this.m = 1 << BUCKET_BITS;// 16384个桶this.buckets = new byte[m];this.constant = getConstant(m);}public void add(String val) {long hash = hash(val);int index = (int) (hash & (m - 1));// 低位连续0+1的数量n 实际估算值 k = 2^n -> 1<<nbyte lowBits = lowBits(hash >>> BUCKET_BITS);if (lowBits > buckets[index]) {buckets[index] = lowBits;}}public long count() {double sum = 0.0;int emptyBuckets = 0;for (byte num : buckets) {sum += 1.0 / (1 << num);if (num == 0) {emptyBuckets++;}}double avg = m / sum; // 调和平均数double estimate = constant * m * avg; // 估算计数值 根据公式// 存在空桶 数据量不够,偏差可能较大 做结果修正if (emptyBuckets > 0 && estimate < (5.0 / 2.0) * m) {// 求对数 空桶数越多 估算结果值越小estimate = m * Math.log((double) m / emptyBuckets);}// 这里先忽略对极大值的修正return Math.round(estimate);}private byte lowBits(long hash) {if (hash == 0) {return 64 - BUCKET_BITS;}int index = 1;while ((hash & 1) == 0) {index++;hash = hash >>> 1;}return (byte) index;}private long hash(String val) {return Hashing.murmur3_128().hashString(val, StandardCharsets.UTF_8).asLong();}private static double getConstant(int buckets) {switch (buckets) {case 16:return 0.673;case 32:return 0.697;case 64:return 0.709;default:return (0.7213 / (1 + 1.079 / buckets));}}
}
结果输出:
实际n 预估n 误差率
1 1 0.0000%
2 2 0.0000%
3 3 0.0000%
4 4 0.0000%
5 5 0.0000%
6 6 0.0000%
7 7 0.0000%
8 8 0.0000%
9 9 0.0000%
10 10 0.0000%
100 100 0.0000%
1000 1003 0.3000%
10000 9989 0.1100%
100000 99717 0.2830%
1000000 999310 0.0690%
10000000 10033112 0.3311%
100000000 99931727 0.0683%
观察结果发现,对估算结果做修正后的 HyperLogLog 算法准确率已经非常高了,在数据规模较小时,修正算法效果非常好。在数据规模较大时,误差率也控制在0.5%以内,我们可以说这是一个可用的版本了,可怕的是它只有七十行代码。
Redis实现
Redis HyperLogLog 和我们 Java 手写的实现思路是一致的,默认也是拆分了 16384 个桶,低 14 位用来定位桶索引号,高 50 位用来计算前导0的位数。
区别是 Redis 对 HyperLogLog 做了一些内存上的优化,分为:稀疏格式和紧凑格式。稀疏格式用在早期阶段,大多数桶都是 0,Redis 直接存储连续 0 桶的数量,而不是把 0 桶全都存一遍。紧凑格式就是完整的 16384 个桶,每个桶占用 6 Bit,一共 12KB 的内存空间。
感兴趣的同学可以去看下源码。
尾巴
HyperLogLog 算法是一种用于估计基数(cardinality)的概率算法,可以高效地计算一个集合中不重复元素的个数。与传统的基数估计方法相比,因为不存储元素本身,所以 HyperLogLog 具有更小的存储空间需求,却能够以极高的准确性给出估计结果。
在不准确绝对准确率的场景下,可以优先考虑 HyperLogLog 算法。
相关文章:

HyperLogLog算法
前言 现在很多站点基本都有统计 PV 和 UV 的需求,PV 的统计很简单,在 Redis 里面维护一个计数器,页面每访问一次计数器就 1,获取 PV 就是读取计数器的值。 相比之下,UV 的统计就比较麻烦了,因为要对用户去…...

自定义Docker镜像--Jupyterlab
概述 自定义Jupyterlab镜像,为deployment做准备 步骤 下载基础镜像:centos:7.9.2009 docker search centos:7.9.2009 docker pull centos:7.9.2009 启动容器 部署应用 # 启动容器 docker run -it --name test centos:7.9.2009 bash# 在容器内部署…...
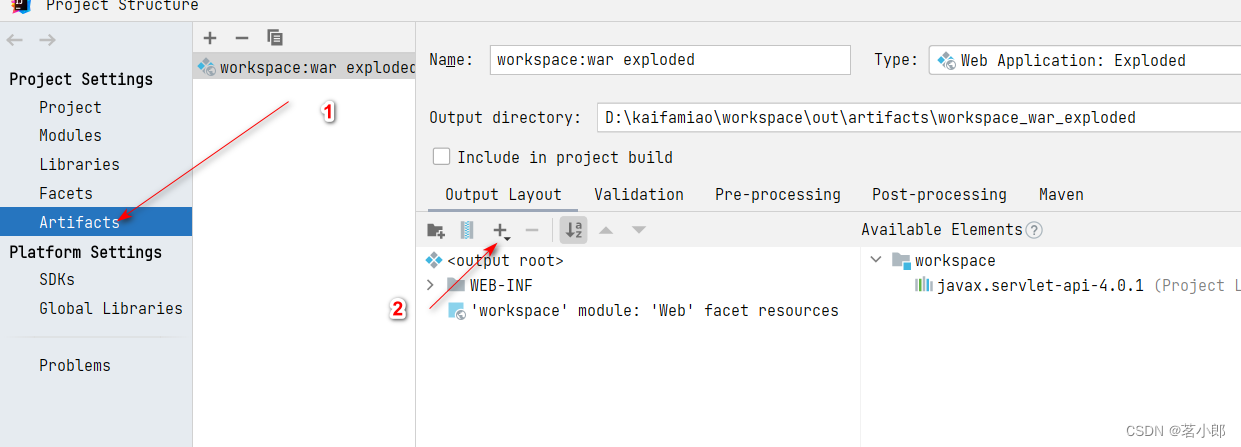
IDEA中明明导入jar包了,依旧报ClassNotFoundException
解决办法: 1.点击IDEA右上角的设置 2.点击Project Structure... 3.点击Artifacts,点击号把包添加下就可以了...

【VIM TMUX】开发工具 Vim 在 bash 中的显示与 tmux 中的显示不同
开发工具 Vim 在 bash 中的显示与 tmux 中的显示不同-CSDN博客 此方法有效 方法如下: 1.在~/.bashrc中添加 alias tmuxtmux -2 ,然后使配置生效 $source ~/.bashrc . 2.在~/.tmux.conf中添加 set -g default-terminal "screen-256color" 完成之后即可…...
全网最全,Postman接口自动化测试实战整理,避开所有弯路...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 背景描述 项目要…...

蓝桥杯双周赛算法心得——三带一(暴力枚举)
大家好,我是晴天学长,枚举思想,需要的小伙伴可以关注支持一下哦!后续会继续更新的。 1) .三带一 2) .算法思路 1.通过Scanner读取输入的整数n,表示接下来有n个字符串需要处理。 2.使用循环遍历每个字符串:…...
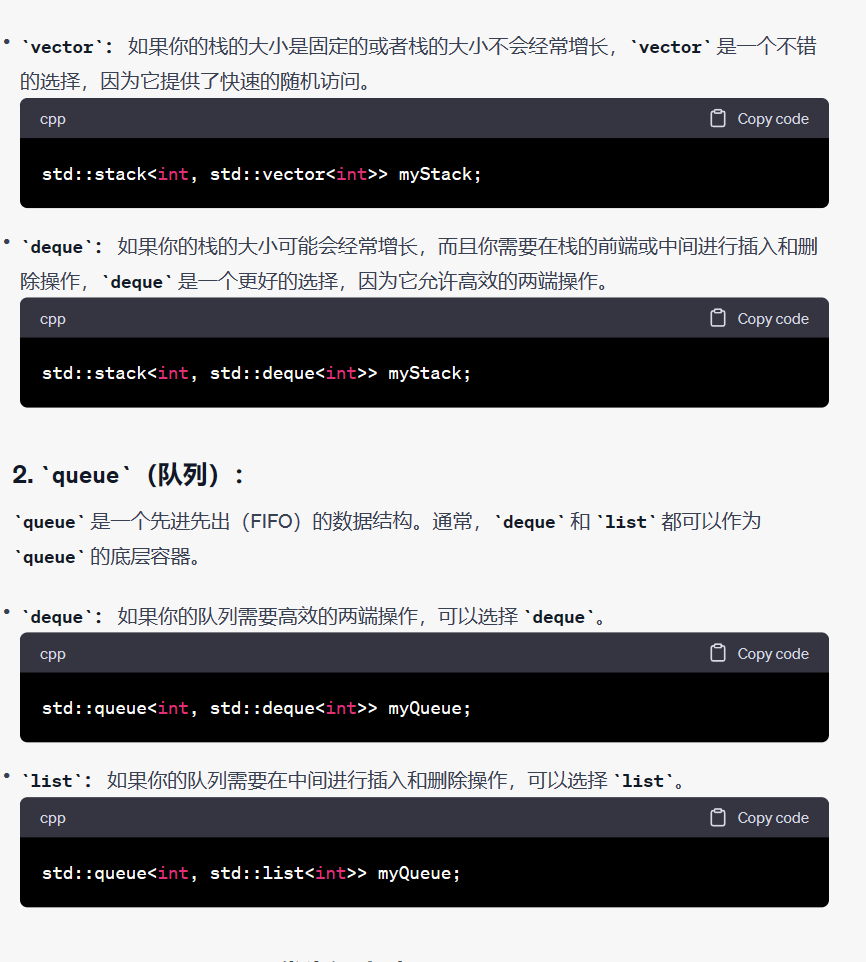
【C++】适配器模式 - - stack/queue/deque
目录 一、适配器模式 1.1迭代器模式 1.2适配器模式 二、stack 2.1stack 的介绍和使用 2.2stack的模拟实现 三、queue 3.1queue的介绍和使用 3.2queue的模拟实现 四、deque(不满足先进先出,和队列无关) 4.1deque的原理介绍 4.2dequ…...
EKP接口开发Webservice服务和Restservice服务以及定时任务Demo
继承com.landray.kmss.sys.webservice2.interfaces.ISysWebservice,同时在接口上使用WebService注解将其标识为WebService接口 package com.landray.kmss.third.notify.webservice;import com.alibaba.fastjson.JSONObject; import com.landray.kmss.sys.webservic…...

如何确定IP地址的具体位置?
IP地址通过几种方法帮助确定具体位置,尽管它们的准确性和精度因不同的情况而异。以下是几种确定具体位置的主要方法: 地理IP数据库:这是最常用的方法之一,它使用IP地址和地理位置数据的映射来确定用户的位置。这些数据库存储了大量…...

软考-网络安全体系与网络安全模型
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 by 2023年10月 网络安全体系相关安全模型 BLP机密性模型 BLP(Biba-格雷泽-麦克拉伦&#x…...

Java身份证OCR识别 - 阿里云API【识别准确率超过99%】
1. 阿里云API市场 https://market.aliyun.com/products/57124001/cmapi00063618.html?spm5176.28261954.J_7341193060.41.60e52f3drduOTh&scm20140722.S_market%40%40API%E5%B8%82%E5%9C%BA%40%40cmapi00063618._.ID_market%40%40API%E5%B8%82%E5%9C%BA%40%40cmapi0006361…...

vue中获取复选框是否被选中的值、如何用JavaScript判断复选框是否被选中
一、方法介绍 第一种方法:通过获取dom元素,getElementById、querySelector、getElementsByName、querySelectorAll(需要遍历,例如:for循环) 第二种是用v-model在input复选框上绑定一个变量,通过…...

Python学习之逻辑中的循环有哪些?
1. for循环 for 循环用于迭代 (遍历)一个序列,例如列表、元组、字符串或字典中的元素。 通常使用 for 循环来遍历可迭代对象中的元素,并对每个元素执行相同的操作。 示例: for item in iterable: # 执行操作2.while循环 -while循环用于在满足某个条件…...
)
【uniapp微信小程序+springBoot(binarywang)
uniapp前端代码 <template><view><page-head :title"title"></page-head><view class"uni-padding-wrap"><view style"background:#FFF; padding:50rpx 0;"><view class"uni-hello-text uni-cente…...
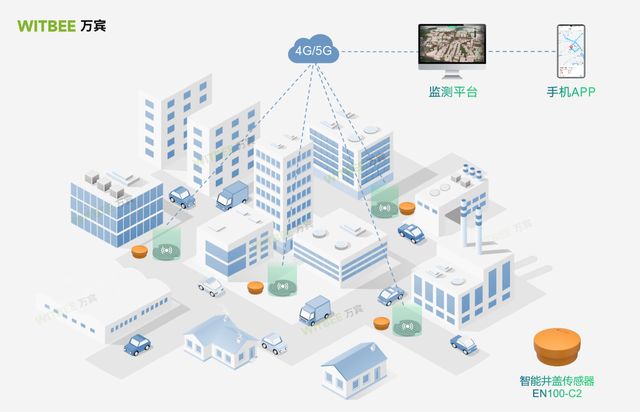
智能井盖的用处有哪些?好用在什么地方?
智能井盖是一种基于物联网技术的井盖系统,通过集成传感器、通信设备和数据处理功能,实现对井盖的实时监测、远程管理和智能化控制。WITBEE万宾的智能井盖传感器EN100-C2,只要在城市需要的井盖上面安装即可使用,一体式结构…...

微信小程序数据存储方式有哪些
在微信小程序中,数据存储方式有以下几种: 本地存储 本地存储是一种轻量级的数据存储方式,用于存储小量的数据,例如用户的配置信息、页面的状态等。微信小程序提供了 wx.setStorage() 和 wx.getStorage() 方法,用于将数…...

FTC局部路径规划代码分析
前置知识: costmap_2d::Costmap2DROS costmap; costmap_2d::Costmap2DROS 是一个ROS包中提供的用于处理2D成本地图的类。它是一个高级的接口,通常用于与ROS导航栈中的导航规划器和本地路径跟踪器等模块进行集成。 costmap 是一个指向 Costmap2DROS 对象的指针。通…...
SpringBoot集成Activiti7
SpringBoot集成Activiti7 SpringBoot版本使用2.7.16 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.7.16</version><relativePath/> <!-- lookup…...
25.1 MySQL SELECT语句
1. SQL概述 1.1 SQL背景知识 1946年, 世界上诞生了第一台电脑, 而今借由这台电脑的发展, 互联网已经成为一个独立的世界. 在过去几十年里, 许多技术和产业在互联网的舞台上兴衰交替. 然而, 有一门技术却从未消失, 甚至日益强大, 那就是SQL.SQL(Structured Query Language&…...

【VSCode】Windows环境下,VSCode 搭建 cmake 编译环境(通过配置文件配置)
除了之前的使用 VSCode 插件来编译工程外,我们也可以使用配置文件来编译cmake工程,主要依赖 launch.json 和 tasks.json 文件。 目录 一、下载编译器 1、下载 Windows GCC 2、选择编译器路径 二、配置 debug 环境 1、配置 lauch.json 文件 2、配置…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
