【Machine Learning】01-Supervised learning
01-Supervised learning
- 1. 机器学习入门
- 1.1 What is Machine Learning?
- 1.2 Supervised learning
- 1.3 Unsupervised learning
- 2. Supervised learning
- 2.1 单元线性回归模型
- 2.1.1 Linear Regression Model(线性回归模型)
- 2.1.2 Cost Function(代价函数)
- 2.1.3 Gradient Descent(梯度下降)
- 2.2 多元线性回归模型
- 2.2.1 Multiple features (variables)
- 2.2.2 针对多元回归的梯度下降
- 2.3 线性回归的实用小技巧
- 2.3.1 Feature Scaling(特征缩放)
- 2.3.2 检查梯度下降是否收敛
- 2.3.3 选择合适的学习率
- 2.3.4 特征工程(Feature Engineering)
- 2.3.5 多项式回归(Polynomial Regression)
- 2.4 Classification(聚类)
- 2.4.1 Logistic Regression(逻辑回归)
- 2.4.2 Decision Boundary(决策边界)
- 2.4.3 Cost Function
- 2.4.4 Simplified Cost Function
- 2.4.5 Gradient Descent
- 2.5 Underfitting and Overfitting
- 2.5.1 概述
- 2.5.2 解决过拟合
- 2.5.3 Regularization(正则化)
- 2.5.4 线性回归模型的正则化
- 2.5.5 逻辑回归模型的正则化
1. 机器学习入门
1.1 What is Machine Learning?
"Field of study that gives computers the ability to learn without being explicitly programmed. "
——Arthur Samuel (1959)
亚瑟·萨缪尔:跳棋程序编写者
常用机器学习算法:
- Supervised learning (more important)
- Unsupervised learning
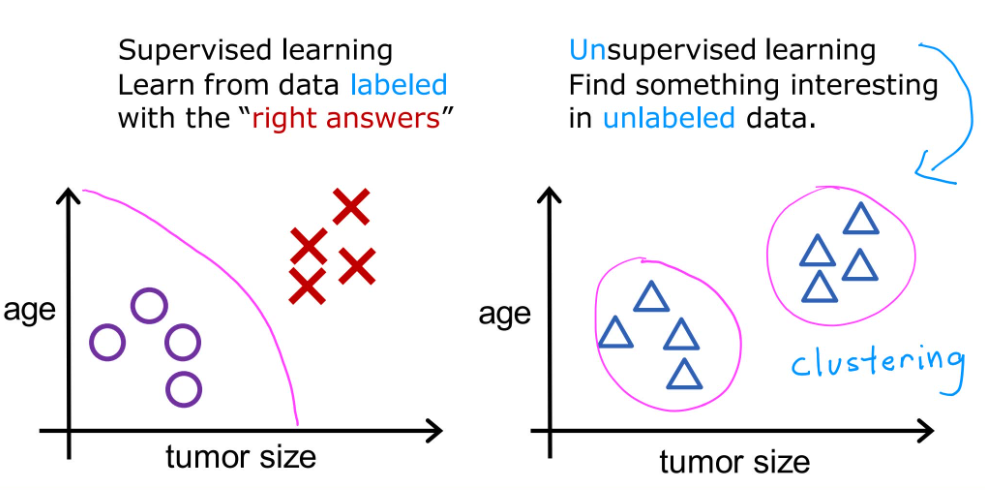
1.2 Supervised learning
监督学习两大类型:
-
Regression(回归)
Predict a number
infinitely many possible outputs
-
Classification(分类)
predict categories
small number of possible outputs
1.3 Unsupervised learning
数据只有输入值x,而没有输出的标签值y,算法会在数据中找到结构,进行分类。
-
Clustering algorithm(聚类)
Group similar data points together
-
Anomaly detection(异常检测)
Find unusual data points
-
Dimensionality reduction(降维)
Compress data using fewer numbers
2. Supervised learning
2.1 单元线性回归模型
2.1.1 Linear Regression Model(线性回归模型)
线性回归模型属于监督学习模型,因为数据集中的每个数据都有确定的值,模型将根据值来进行学习。
Terminology(术语):
Training Set: Data used to train the model
Notation:
- x x x = “input” variable / “input” feature / feature
- y y y = “output” variable / “target” feature /
- m m m = number of training examples
- ( x , y ) (x, y) (x,y) = single training example
- ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i)) = i t h i^{th} ith training example
m o d e l : f w , b ( x ) = w x + b model: \quad f_{w,b}(x) = wx+b model:fw,b(x)=wx+b
“w” means weight / slope, “b” means bias / intercept
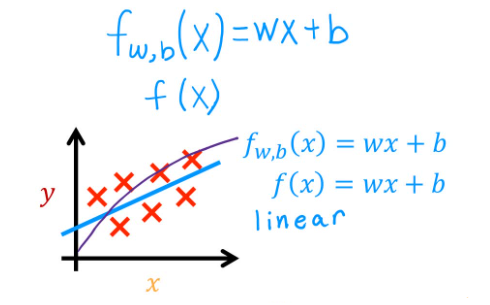
2.1.2 Cost Function(代价函数)
显然,我们希望选取的模型能够很好的拟合训练集中的数据,这就需要一个参数来量化当前的拟合程度,这就是Cost Function。其中m表示测试集样本的总数,在公式中用于避免代价函数盲目增大,设置为2m是为了便于求导。
J ( w , b ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 J(w,b) = \frac{1}{2m} \sum_{i=1}^m (\hat{y}^{(i)} - y^{(i)})^2 = \frac{1}{2m} \sum_{i=1}^m (f_{w,b}(x^{(i)}) - y^{(i)})^2 J(w,b)=2m1i=1∑m(y^(i)−y(i))2=2m1i=1∑m(fw,b(x(i))−y(i))2
可见,代价函数越大,拟合效果越差。于是,线性回归模型的目标就是找到最小的w值,使得 J ( w ) J(w) J(w)最小化;更普遍的情况是,找到最小的w和b值,使得 J ( w , b ) J(w,b) J(w,b)最小化。
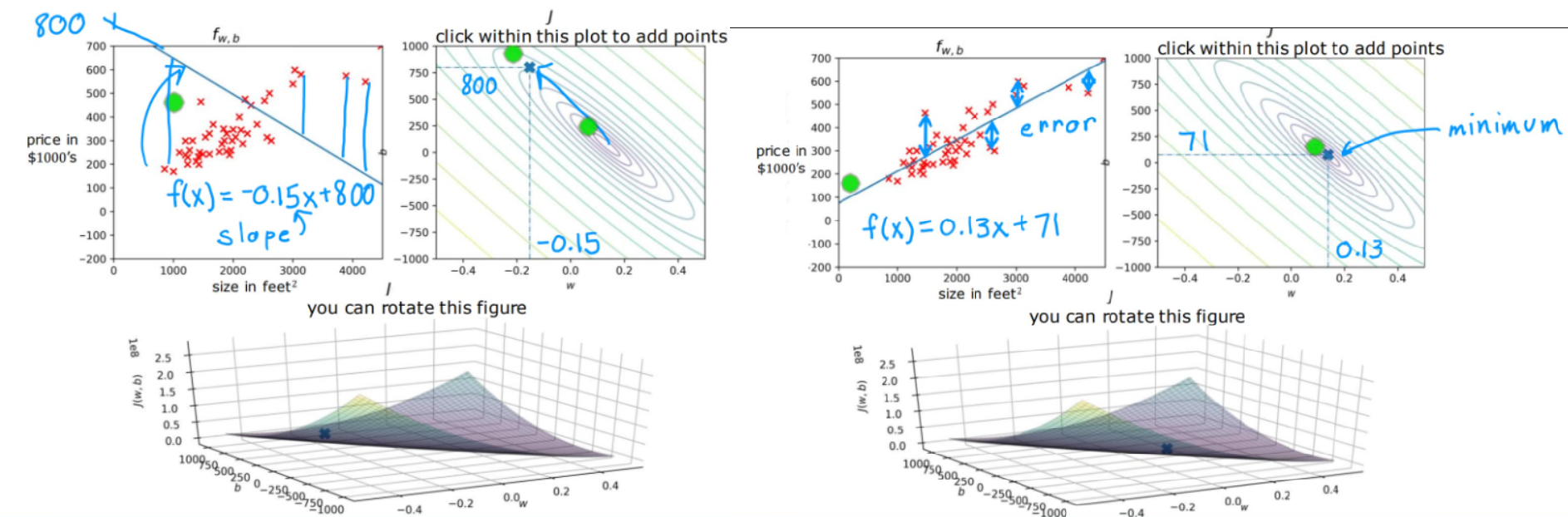
在经典房价预测案例中,我们选取房屋面积作为特征,根据不同的参数可以得到下面的三维图像,纵坐标为代价函数大小,很直观的看到右图中的代价函数要更小,同时也不难看出右图的取值更好的拟合了测试集。
2.1.3 Gradient Descent(梯度下降)
有了代价函数,如何得到合适的参数值就成为了必须解决的问题。通过Gradient Descent,我们可以获得代价最小的参数w和b。
梯度下降算法广泛应用于机器学习,如线性回归模型和深度学习模型中。
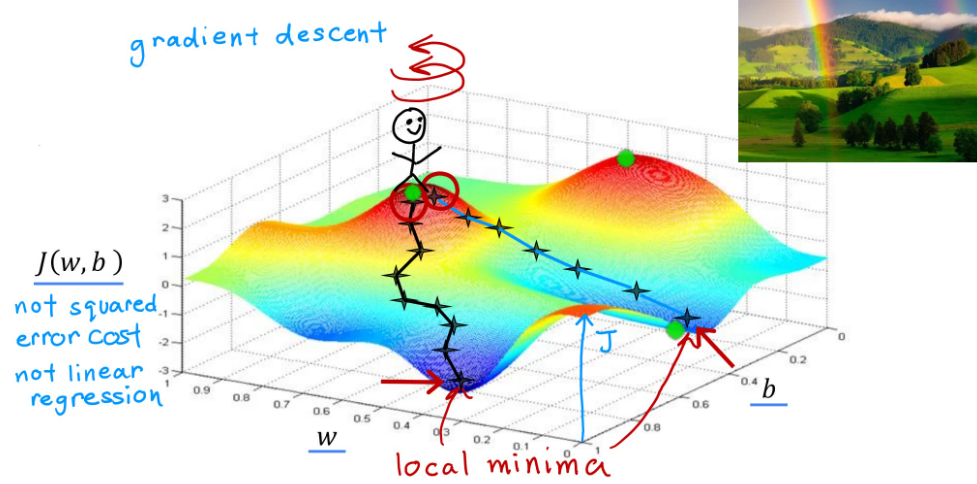
在上面的曲面中,通过不断选择当前坐标坡度最大的方向,最终会到达谷底,谷底即local minima,即局部最小值。
梯度下降算法概述:
让 w , b w,b w,b以某值开始,通过不断改变 w , b w,b w,b来降低 J ( w , b ) J(w, b) J(w,b),直到取得或接近 J ( w , b ) J(w, b) J(w,b)最小值,即:Repeat until convergence(重复,直到收敛)。
r e p e a t { w = w − α ∂ ∂ w J ( w , b ) b = b − α ∂ ∂ b J ( w , b ) } s i m u l t a n e o u s u p d a t e s \begin{align} & repeat\{ \\ &\qquad w = w - α \frac{∂}{∂w}J(w,b) \\ &\qquad b = b - α \frac{∂}{∂b}J(w,b) \\ & \}simultaneous \quad updates \end{align} repeat{w=w−α∂w∂J(w,b)b=b−α∂b∂J(w,b)}simultaneousupdates
α = L e a r n i n g R a t e α = Learning \ Rate α=Learning Rate,即学习率,控制梯度下降的步长;
∂ ∂ w = D e r i v a t i v e \frac{∂}{∂w} = Derivative ∂w∂=Derivative,即导数项(偏导数,Partial derivative),控制梯度下降的方向。
2.2 多元线性回归模型
2.2.1 Multiple features (variables)
很多实际情况并不止有一个特征,比如决定房价的不只有面积。对于有多个特征的线性回归模型,我们称为多元线性回归模型。
x j x_j xj = j t h j^{th} jth feature
n n n = number of features
x ⃗ ( i ) \vec{x}^{(i)} x(i) = features of i t h i^{th} ith training example
x ⃗ j ( i ) \vec{x}^{(i)}_j xj(i) = value of feature j j j in i t h i^{th} ith training example
M o d e l : f w , b ( x ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + w 4 x 4 + b Model: \quad f_{w,b}(x) = w_1x_1+w_2x_2+w_3x_3+w_4x_4+b Model:fw,b(x)=w1x1+w2x2+w3x3+w4x4+b
进一步可以表达为:
f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b f_{\vec{w},b}(\vec{x}) = \vec{w}·\vec{x}+b fw,b(x)=w⋅x+b
在Python中,向量的计算可以通过调用NumPy库,实现快速且间接的运算,其中,w和x均为向量
w = np.array([1.0, 2.5, -3.3])
b = 4
x = np.array([10, 20, 30])f = np.dot(w, x) + b
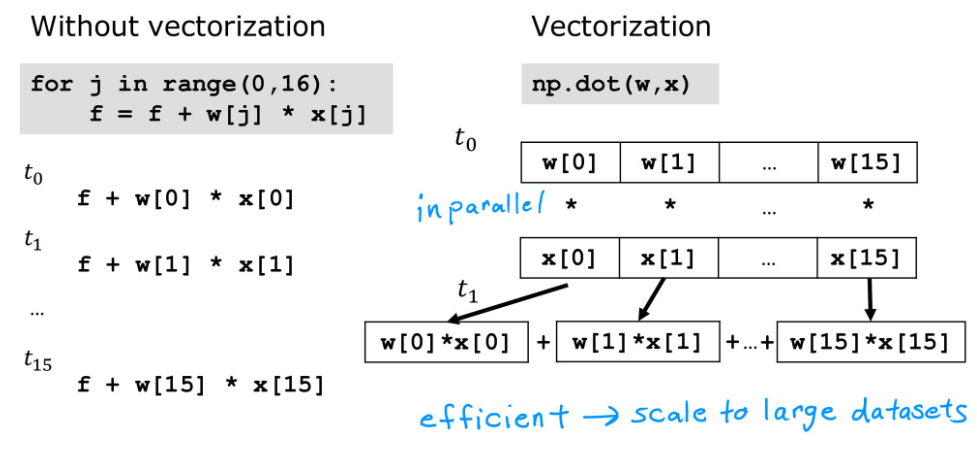
通过向量化运算,计算机同时获取向量的所有数据,并且对两向量的每个维度进行同时运算,然后调用专门的并行处理硬件求和;而左侧的for循环则是依次相乘并累加。显然,使用向量可以节省很大的时间。
2.2.2 针对多元回归的梯度下降
| Previous notation | Vector notation | |
|---|---|---|
| Parameters | w 1 , ⋅ ⋅ ⋅ , w n w_1,···,w_n w1,⋅⋅⋅,wn b b b | w ⃗ = [ w 1 ⋅ ⋅ ⋅ w n ] \vec{w}=[w_1 ··· w_n] w=[w1⋅⋅⋅wn] b b b |
| Model | f w , b ( x ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + w 4 x 4 + b f_{w,b}(x) = w_1x_1+w_2x_2+w_3x_3+w_4x_4+b fw,b(x)=w1x1+w2x2+w3x3+w4x4+b | f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b f_{\vec{w},b}(\vec{x})=\vec{w}·\vec{x}+b fw,b(x)=w⋅x+b |
| Cost function | J ( w 1 , ⋅ ⋅ ⋅ , w n , b ) J(w_1,···,w_n,b) J(w1,⋅⋅⋅,wn,b) | J ( w ⃗ , b ) J(\vec{w},b) J(w,b) |
| Gradient descent | repeat{ w j = w j − α ∂ ∂ w j J ( w 1 , ⋅ ⋅ ⋅ , w n , b ) w_j=w_j-α\frac{∂}{∂w_j}J(w_1,···,w_n,b) wj=wj−α∂wj∂J(w1,⋅⋅⋅,wn,b) b = b − α ∂ ∂ b J ( w 1 , ⋅ ⋅ ⋅ , w n , b ) b=b-α\frac{∂}{∂b}J(w_1,···,w_n,b) b=b−α∂b∂J(w1,⋅⋅⋅,wn,b) } | repeat{ w j = w j − α ∂ ∂ w j J ( w ⃗ , b ) w_j=w_j-α\frac{∂}{∂w_j}J(\vec{w},b) wj=wj−α∂wj∂J(w,b) b = b − α ∂ ∂ b J ( w ⃗ , b ) b=b-α\frac{∂}{∂b}J(\vec{w},b) b=b−α∂b∂J(w,b) } |
【梯度下降法扩展】Normal equation(正规方程法):
正规方程法:不需要通过迭代即可求得w,b的值,同时只能用在线性回归模型中。
缺点:不适用于其他学习算法,当特征的数量极大时(如大于10000)计算速度减慢。
在实现线性回归的机器学习库中可以使用正规方程方法,但是梯度下降是寻找参数w,b的推荐方法。
2.3 线性回归的实用小技巧
2.3.1 Feature Scaling(特征缩放)
下式为房价案例的线性回归模型, x 1 x_1 x1表示房子大小(size,单位:feet²), x 2 x_2 x2表示卧室数量(#badrooms)
p r i c e ^ = w 1 x 1 + w 2 x 2 + b \hat{price}=w_1x_1+w_2x_2+b price^=w1x1+w2x2+b
我们可以假设: x 1 x_1 x1范围为500-2000, x 2 x_2 x2范围为0-5,这都是现实中合理的数据范围,但是当我们给参数 w 1 , w 2 w_1,w_2 w1,w2不同的值,也会得到不同的效果,左侧数据显然不符合实际,这是因为在经典房价案例中,房屋面积的参数对结果的影响更大,而卧室数量的参数影响则较小。

观察下图中左上坐标系,点的位置由于两特征的范围原因,不利于观察;右上坐标系的等高线也不利于进行梯度下降。如果对变量进行Feature Scaling,即特征缩放,改变他们的相对范围,就会使数据分布更合理,梯度下降速度更快
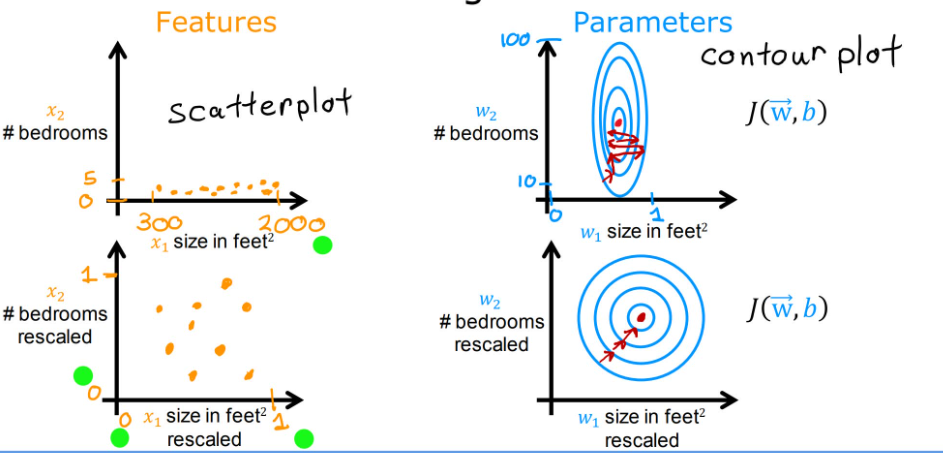
那么如何进行特征缩放呢?
方法一:
对于房屋案例, x 1 x_1 x1的取值范围是500~2000,只需要进行 x 1 , s c a l e d = x 1 2000 x_{1,scaled}=\frac{x_1}{2000} x1,scaled=2000x1,就可以将之范围缩放到0.15~1
同理, x 2 x_2 x2的取值范围是0~5,只需要进行 x 2 , s c a l e d = x 2 5 x_{2,scaled}=\frac{x_2}{5} x2,scaled=5x2,就可以将之范围缩放到0~1
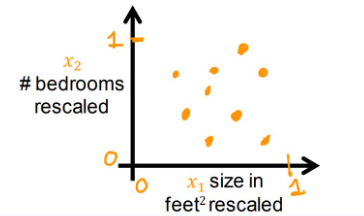
方法二:Mean normalization(均值归一化)
通过缩放将数据点聚集在坐标轴原点的四周(意味着有正负值),范围在-1~1之间
首先求 x 1 x_1 x1和 x 2 x_2 x2在训练集上的均值 μ 1 \mu_1 μ1和 μ 2 \mu_2 μ2
然后进行: x 1 , s c a l e d = x 1 − μ 1 2000 − 300 x_{1,scaled}=\frac{x_1-\mu_1}{2000-300} x1,scaled=2000−300x1−μ1以及 x 2 , s c a l e d = x 2 − μ 2 5 − 0 x_{2,scaled}=\frac{x_2-\mu_2}{5-0} x2,scaled=5−0x2−μ2
这样 x 1 x_1 x1被缩放到-0.18~0.82, x 2 x_2 x2则被缩放到-0.45~0.54
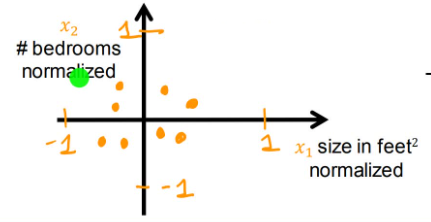
方法三:Z-score normalization(Z-score归一化)
需要为每一个特征进行计算标准差(standard deviation)以及均值
然后进行: x 1 , s c a l e d = x 1 − μ 1 σ 1 x_{1,scaled}=\frac{x_1-\mu_1}{\sigma_1} x1,scaled=σ1x1−μ1以及 x 2 , s c a l e d = x 2 − μ 2 σ 2 x_{2,scaled}=\frac{x_2-\mu_2}{\sigma_2} x2,scaled=σ2x2−μ2
这样 x 1 x_1 x1被缩放到-0.67~3.1, x 2 x_2 x2则被缩放到-1.6~1.9
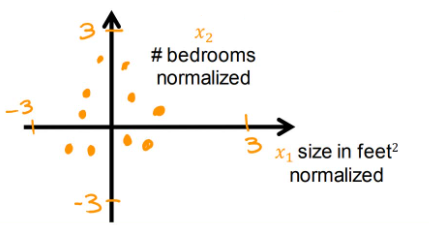
总而言之,缩放的范围以及缩放应当选择哪个方法都没有具体的规定,但通过缩放,特征的量级应当相同,否则缩放就没有意义了,梯度下降速度也得不到提升。
2.3.2 检查梯度下降是否收敛
我们应当保证梯度下降算法正确工作。为此,可以构建一个横轴为迭代次数(# iterations),纵轴为代价 J ( w ⃗ , b ) J(\vec{w},b) J(w,b)的坐标轴,正确的图像应当是随着迭代次数增加,代价不断下降直至平缓。我们称这条曲线为学习曲线(learning curve)。
在不同的运用场景中,梯度下降的收敛速度可能有很大差异。
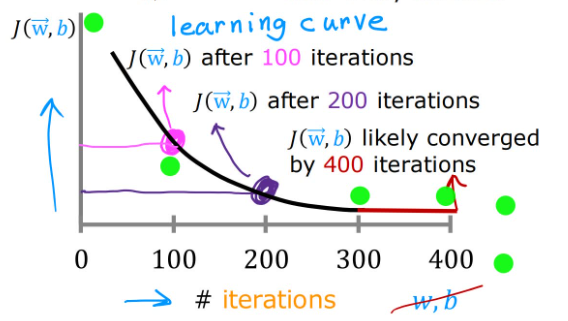
如何通过数学方法来确定收敛?
进行Automatic convergence test(自动收敛实验)。
例如:令 ϵ \epsilon ϵ为 1 0 − 3 10^{-3} 10−3,在一次迭代中,如果 J ( w ⃗ , b ) J(\vec{w},b) J(w,b)的下降值小于 ϵ \epsilon ϵ,我们认为梯度下降收敛。
但是选定一个合适的 ϵ \epsilon ϵ也是比较困难的,所以应当结合学习曲线,进行观察。
2.3.3 选择合适的学习率
当出现了下图中的情况时,我们认为可能是代码中有bug或者learning rate过大。这是因为当学习率过大时,w的修改也会变大,因此而造成代价不降反增。
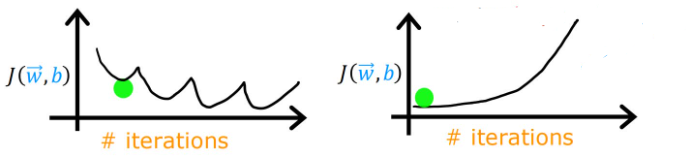
我们可以将α设置为很小的数字,观察迭代过程中代价是否下降,如果此时依然会有波动,那就应该是代码中出现了bug。确定不存在bug后,再逐步增大α,以求更快速的梯度下降。
2.3.4 特征工程(Feature Engineering)
实际问题中的特征往往不只一个,而且我们应当为模型选择合适的特征值,并且对已有特征进行组合获得新的特征。
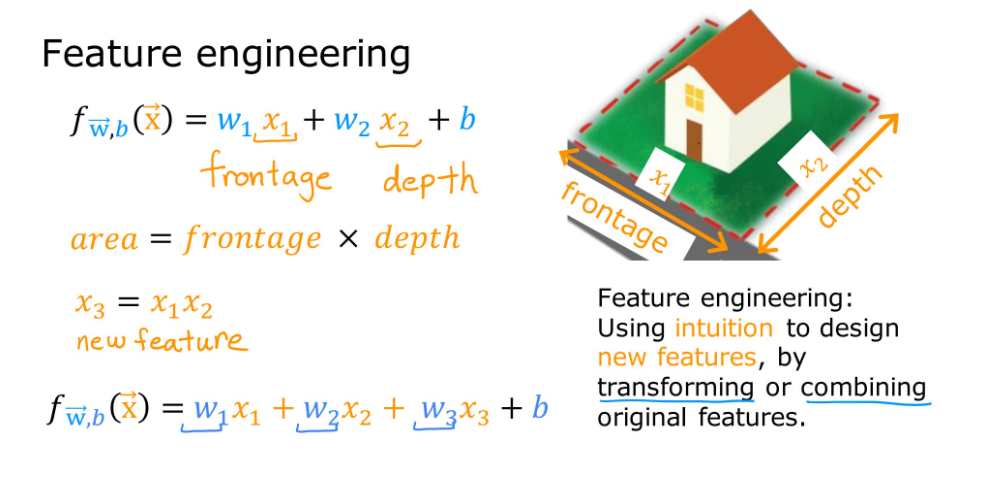
2.3.5 多项式回归(Polynomial Regression)
一次多项式
f w ⃗ , b ( x ) = w 1 x + b f_{\vec{w},b}(x) = w_1x+b fw,b(x)=w1x+b
二次多项式
f w ⃗ , b ( x ) = w 1 x + w 2 x 2 + b f_{\vec{w},b}(x) = w_1x+w_2x^2+b fw,b(x)=w1x+w2x2+b
三次多项式
f w ⃗ , b ( x ) = w 1 x + w 2 x 2 + w 3 x 3 + b f_{\vec{w},b}(x) = w_1x+w_2x^2+w_3x^3+b fw,b(x)=w1x+w2x2+w3x3+b
二次方根多项式
f w ⃗ , b ( x ) = w 1 x + w 2 x + b f_{\vec{w},b}(x) = w_1x+w_2\sqrt{x}+b fw,b(x)=w1x+w2x+b
2.4 Classification(聚类)
2.4.1 Logistic Regression(逻辑回归)
【注】此部分内容在西瓜书上被写作“对数几率回归”
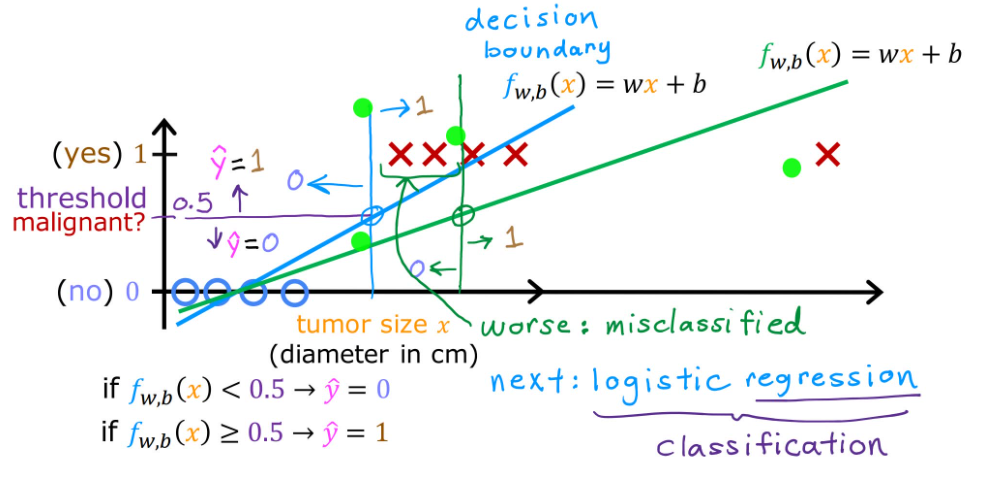
有很多现实问题的答案是“是”或者“否”,这样的问题我们称之为二元分类(binary classification)。对于二元分类问题,如果我们通过线性回归进行拟合,就会产生误差。
比如在恶性肿瘤分类的问题中,如果已经进行了拟合,现加入新的坐标点,就可能会出现错误分类。线性拟合显然已无法满足分类问题,我们通过逻辑回归来处理该类问题。
首先引入Sigmoid function(Sigmoid函数),也被称为logistic function(逻辑函数),显然Sigmoid函数的值域为0到1。
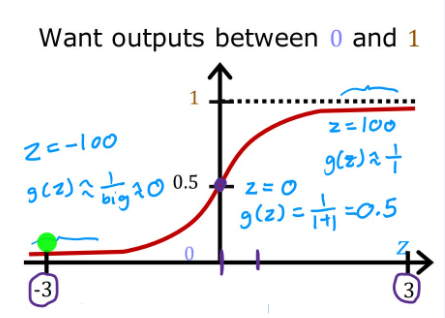
如果用 g ( z ) g(z) g(z)来表示这个函数,那么:
g ( z ) = 1 1 + e − z , 0 < g ( z ) < 1 g(z)=\frac{1}{1+e^{-z}},0<g(z)<1 g(z)=1+e−z1,0<g(z)<1
M o d e l : f w ⃗ , b ( x ⃗ ) = g ( w ⃗ ⋅ x ⃗ + b ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) Model:f_{\vec{w},b}(\vec{x})=g(\vec{w}·\vec{x}+b)=\frac{1}{1+e^{-(\vec{w}·\vec{x}+b)}} Model:fw,b(x)=g(w⋅x+b)=1+e−(w⋅x+b)1
在恶行肿瘤判断案例中,x即为肿瘤大小,y为是否是恶性肿瘤的二元分类,如果一位病人的肿瘤根据计算为 f w ⃗ , b ( x ⃗ ) = 0.7 f_{\vec{w},b}(\vec{x})=0.7 fw,b(x)=0.7,我们就认为模型告诉我们这位病人的肿瘤有70%的概率为恶性的。
由于 P ( y = 0 ) + P ( y = 1 ) = 1 P(y=0)+P(y=1)=1 P(y=0)+P(y=1)=1,我们也可以说,这位病人的肿瘤有30%的概率为良性的。
有时会有这样的描述,这个式子表示,在给定输入特征的前提下(x为输入,w和b为参数),y等于1的概率是多少(条件概率)。
f w ⃗ , b ( x ⃗ ) = P ( y = 1 ∣ x ⃗ ; w ⃗ , b ) f_{\vec{w},b}(\vec{x})=P(y=1|\vec{x};\vec{w},b) fw,b(x)=P(y=1∣x;w,b)
2.4.2 Decision Boundary(决策边界)
根据Sigmoid函数,我们获得了新模型来描述逻辑回归模型:
f w ⃗ , b ( x ⃗ ) = g ( w ⃗ ⋅ x ⃗ + b ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) = P ( y = 1 ∣ x ⃗ ; w ⃗ , b ) f_{\vec{w},b}(\vec{x})=g(\vec{w}·\vec{x}+b)=\frac{1}{1+e^{-(\vec{w}·\vec{x}+b)}}=P(y=1|\vec{x};\vec{w},b) fw,b(x)=g(w⋅x+b)=1+e−(w⋅x+b)1=P(y=1∣x;w,b)
当 f w ⃗ , b ( x ⃗ ) > = 0.5 f_{\vec{w},b}(\vec{x})>=0.5 fw,b(x)>=0.5,我们认为 y ^ = 1 \hat{y}=1 y^=1;当 f w ⃗ , b ( x ⃗ ) < 0.5 f_{\vec{w},b}(\vec{x})<0.5 fw,b(x)<0.5,我们认为 y ^ = 0 \hat{y}=0 y^=0。所以,什么情况下有 f w ⃗ , b ( x ⃗ ) > = 0.5 f_{\vec{w},b}(\vec{x})>=0.5 fw,b(x)>=0.5 ?
f w ⃗ , b ( x ⃗ ) > = 0.5 = > g ( z ) > = 0.5 = > z > = 0 = > w ⃗ ⋅ x ⃗ + b > = 0 < = > y ^ = 1 \begin{align} &f_{\vec{w},b}(\vec{x}) >= 0.5 \\ &=> \quad g(z) >= 0.5 \\ &=> \quad z >= 0 \\ &=> \quad \vec{w}·\vec{x} + b >= 0 \\ &<=>\quad \hat{y} = 1 \end{align} fw,b(x)>=0.5=>g(z)>=0.5=>z>=0=>w⋅x+b>=0<=>y^=1
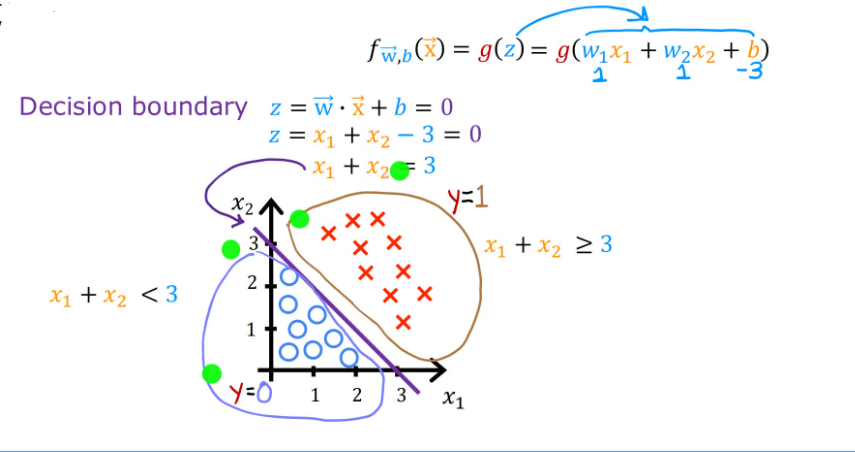
当 w ⃗ ⋅ x ⃗ + b = 0 \vec{w}·\vec{x}+b=0 w⋅x+b=0时,这条线就表示决策边界。下图分别为线性决策边界和非线性决策边界。

2.4.3 Cost Function

现有上述training set,应当如何选取w向量和b?
如果选取平方误差代价函数(Squared error cost function): J ( w ⃗ , b ) = 1 m ∑ i = 1 m 1 2 ( f w ⃗ , b ( x ( i ) ) − y ( i ) ) 2 J(\vec{w},b) = \frac{1}{m} \sum_{i=1}^m \frac{1}{2}(f_{\vec{w},b}(x^{(i)}) - y^{(i)})^2 J(w,b)=m1∑i=1m21(fw,b(x(i))−y(i))2。那么线性回归模型和逻辑回归模型的代价函数图大概如下所示:
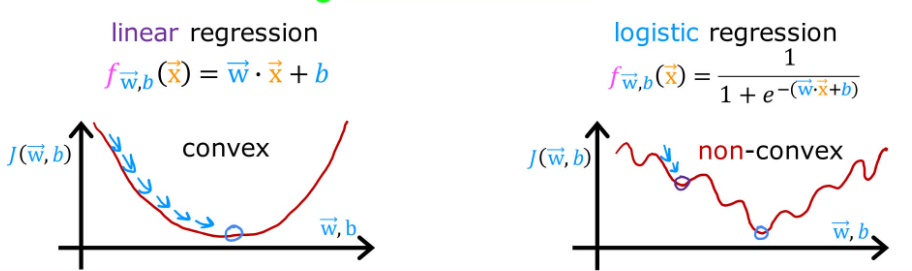
【convex】adj. 凸面的;n. 凸面
对于逻辑回归模型,平方误差代价函数显然不好,因为产生了很多局部极小值,这就使梯度下降过程中会卡在这些地方。所以应当构建一个新的函数,来让代价函数重新凸化。
我们修改一下代价函数 J ( w ⃗ , b ) J(\vec{w},b) J(w,b)的定义:
我们把函数 L ( f w ⃗ , b ( x ( i ) ) , y ( i ) ) L(f_{\vec{w},b}(x^{(i)}) , y^{(i)}) L(fw,b(x(i)),y(i))称为单个训练例子的损失(the loss on a single training example),称之为损失函数
KaTeX parse error: Expected 'EOF', got '&' at position 29: …oss \ function:&̲ L(f_{\vec{w},b…
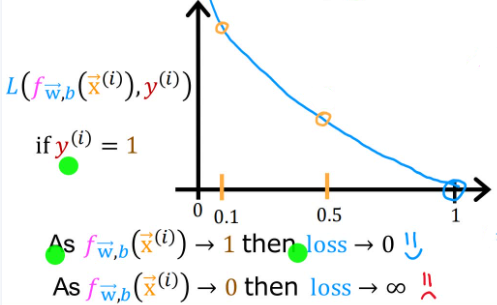
当 y ( i ) = 1 y^{(i)}=1 y(i)=1(即真实值为1):
- 如果 f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w},b}(\vec{x}^{(i)}) fw,b(x(i))趋于1(即预测值趋于1),那么损失就趋于0,说明预测很准确
- 如果 f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w},b}(\vec{x}^{(i)}) fw,b(x(i))趋于0,那么损失就趋于无穷大
- 这就意味预测值离真实值越远,损失越大,反之越小
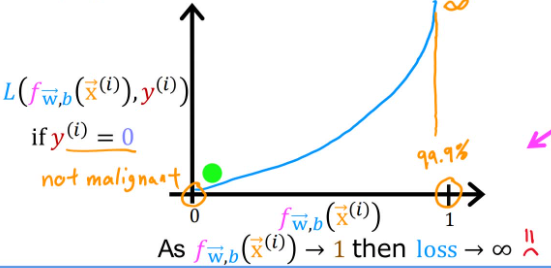
当 y ( i ) = 0 y^{(i)}=0 y(i)=0(即真实值为0):
- 如果 f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w},b}(\vec{x}^{(i)}) fw,b(x(i))趋于0(即预测值趋于0),那么损失就趋于0,说明预测很准确
- 如果 f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w},b}(\vec{x}^{(i)}) fw,b(x(i))趋于1,那么损失就趋于无穷大
通过上文的叙述,我们归纳出针对逻辑回归的代价函数以及损失函数:
J ( w ⃗ , b ) = 1 m ∑ i = 1 m L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) = { − l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) , i f y ( i ) = 1 − l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) , i f y ( i ) = 0 J(\vec{w},b) = \frac{1}{m} \sum_{i=1}^m L(f_{\vec{w},b}(\vec{x}^{(i)}) , y^{(i)}) \\ \\ L(f_{\vec{w},b}(\vec{x}^{(i)}) , y^{(i)})= \begin{cases} -log(f_{\vec{w},b}(\vec{x}^{(i)}))&,if\ \ y^{(i)}=1\\ -log(1-f_{\vec{w},b}(\vec{x}^{(i)}))&,if\ \ y^{(i)}=0 \end{cases} J(w,b)=m1i=1∑mL(fw,b(x(i)),y(i))L(fw,b(x(i)),y(i))={−log(fw,b(x(i)))−log(1−fw,b(x(i))),if y(i)=1,if y(i)=0
之前针对线性回归的代价函数为:
J ( w ⃗ , b ) = 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ( i ) ) − y ( i ) ) 2 J(\vec{w},b) = \frac{1}{2m} \sum_{i=1}^m (f_{\vec{w},b}(x^{(i)}) - y^{(i)})^2 J(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2
2.4.4 Simplified Cost Function
我们可以将上节中得出的分段损失函数改写为下式,通过简单分析就可以得出新式与原式是等价的。
L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) = − y ( i ) l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) L(f_{\vec{w},b}(\vec{x}^{(i)}) , y^{(i)})= -y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)})) -(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)})) L(fw,b(x(i)),y(i))=−y(i)log(fw,b(x(i)))−(1−y(i))log(1−fw,b(x(i)))
于是简化后的代价函数就是:
J ( w ⃗ , b ) = 1 m ∑ i = 1 m [ L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) ] = − 1 m ∑ i = 1 m [ y ( i ) l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] J(\vec{w},b)= \frac{1}{m} \sum_{i=1}^m [L(f_{\vec{w},b}(\vec{x}^{(i)}) , y^{(i)})]= -\frac{1}{m} \sum_{i=1}^m [ y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)})) +(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)})) ] J(w,b)=m1i=1∑m[L(fw,b(x(i)),y(i))]=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]
2.4.5 Gradient Descent
r e p e a t { w j = w j − α ∂ ∂ w J ( w ⃗ , b ) = w j − α [ 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) ] b = b − α ∂ ∂ b J ( w ⃗ , b ) = b − α [ 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ] } s i m u l t a n e o u s u p d a t e s \begin{align} &repeat \{ \\ &\qquad w_j = w_j - α \frac{∂}{∂w} J(\vec{w},b) = w_j - α [ \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} ] \\ &\qquad b = b - α \frac{∂}{∂b} J(\vec{w},b) = b - α [ \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) ] \\ &\} simultaneous \quad updates \end{align} repeat{wj=wj−α∂w∂J(w,b)=wj−α[m1i=1∑m(fw,b(x(i))−y(i))xj(i)]b=b−α∂b∂J(w,b)=b−α[m1i=1∑m(fw,b(x(i))−y(i))]}simultaneousupdates
对于逻辑回归中的梯度下降参数,我们同样进行同步更新,上式中求偏导后的式子恰好与线性回归中式子相同,但他们的含义并不同。
这是因为在Linear regression中: f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b f_{\vec{w},b}(\vec{x}) = \vec{w} · \vec{x} + b fw,b(x)=w⋅x+b;但是在Logistic regression中: f w ⃗ , b ( x ⃗ ) = g ( w ⃗ ⋅ x ⃗ + b ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) f_{\vec{w},b}(\vec{x}) = g(\vec{w} · \vec{x} + b) = \frac{1}{1 + e^{-(\vec{w} · \vec{x} + b)}} fw,b(x)=g(w⋅x+b)=1+e−(w⋅x+b)1,但二者都可以进行梯度下降监视。
2.5 Underfitting and Overfitting
2.5.1 概述
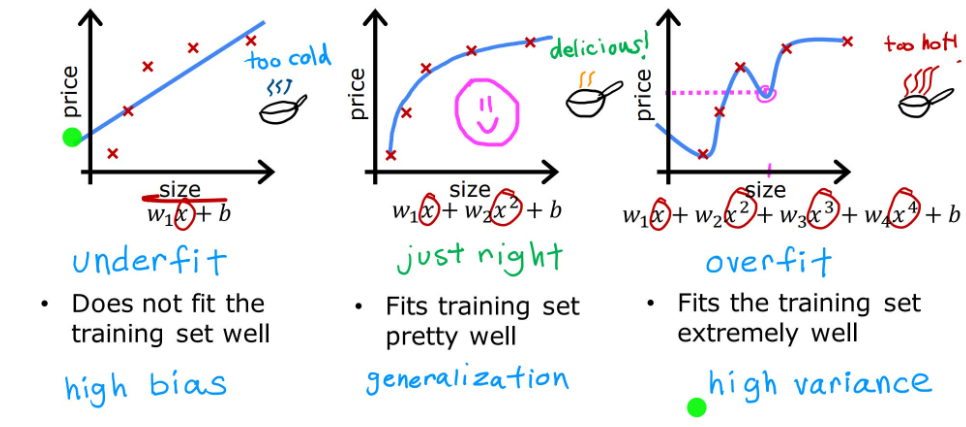
在经典房价预测案例中,假定已获得上图中的数据,并将这些数据作为测试集进行拟合。
若选用一次多项式进行拟合,显然与趋势不同,因为当面积越来越大,房价也趋于平稳,不会像一次函数一样无限增长。我们称这样的结果为欠拟合(Underfitting)或高偏差(high bias)。
如果选用更高次项的多项式,得到的结果十分准确的拟合了数据集中的每一个训练数据,代价函数也几乎等于零。但这是一条很波动的曲线,有时当面积增加房价反而大幅下降,这显然也与实际不符。我们称这样的结果为过拟合(Overfitting)或高方差(high variance)。
欠拟合和过拟合的模型都不具备泛化(generalization)新样本的能力。

同理,对于逻辑回归模型,也有类似的拟合情况。上图是恶行肿瘤判断案例, x 1 x_1 x1表示患者年龄, x 2 x_2 x2表示肿瘤大小。
2.5.2 解决过拟合
-
Collect more training examples
应对过拟合的方法之一就是搜集更多的测试数据,不断添加新的数据后,过拟合将逐步被解决。但如果无法获取足够多的测试数据,该方法就失效了。
-
Select features to include/exclude
造成过拟合的原因之一可能是选取的特征过多了,有时应当对特征进行舍弃,减少特征的数量也是解决过拟合的方法之一。但如果如此多的特征确实都是无法舍弃的,该方法就失效了。
-
Regularization
正则化是对特征的参数进行缩小,即减小某特征的权重,而非像方法二一样直接删除掉这个特征。即:保留所有特征,但防止权重过大造成过拟合。
2.5.3 Regularization(正则化)
以线性回归模型为例,其代价函数为 J ( w ⃗ , b ) = 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 J(\vec{w},b) = \frac{1}{2m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})^2 J(w,b)=2m1∑i=1m(fw,b(x(i))−y(i))2。
当过度追求最小化代价函数,即 m i n w ⃗ , b { J ( w ⃗ , b ) } = m i n w ⃗ , b { 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 } \underset{\vec{w},b}{min} \ \{J(\vec{w},b) \} = \underset{\vec{w},b}{min} \ \{\frac{1}{2m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})^2\} w,bmin {J(w,b)}=w,bmin {2m1∑i=1m(fw,b(x(i))−y(i))2},就会出现上文中过拟合的情况,显然过拟合时,代价函数的值要比“just right”时代价函数的值要小。所以应当优化代价函数的公式,不应该只考虑估计值与真实值的差距,也应当考虑不同多项式的权重。
比如当下右图中 x 3 , x 4 x^3,x^4 x3,x4的系数 w 3 , w 4 w_3,w_4 w3,w4趋于0时,拟合曲线就会更加平滑,接近下左图的情况。
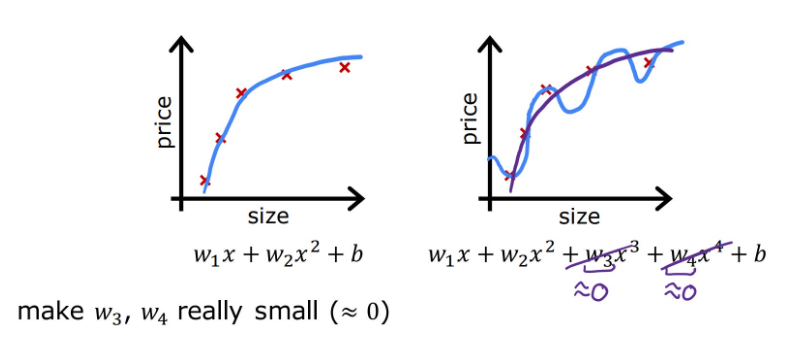
现将代价函数修改为下式,1000为任意给定的一个较大的数字,旨在进行说明而非强制为1000。
m i n w ⃗ , b { J ( w ⃗ , b ) } = m i n w ⃗ , b { 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 + 1000 w 3 2 + 1000 w 4 2 } \underset{\vec{w},b}{min} \{J(\vec{w},b)\} = \underset{\vec{w},b}{min} \{ \frac{1}{2m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})^2 + 1000w_3^2 + 1000w_4^2 \} w,bmin{J(w,b)}=w,bmin{2m1i=1∑m(fw,b(x(i))−y(i))2+1000w32+1000w42}
此时,如果继续追求最小化代价函数, w 3 , w 4 w_3,w_4 w3,w4也被纳入了考虑范围,并且越小越好。当得到最小化后的代价函数时,由于 x 3 , x 4 x^3,x^4 x3,x4的系数 w 3 , w 4 w_3,w_4 w3,w4趋于0(也称为:对 w 3 , w 4 w_3,w_4 w3,w4进行了惩罚),图像更加趋于二次函数的样子,这样就大幅度消除了过拟合带来的影响,这就是正则化的思想。
但是正则化过程中我们往往无法直接确定哪个特征应当被惩罚,所以正则化的实现通常是惩罚所有特征,现在建立一个对所有特征都进行惩罚的模型,其中, λ \lambda λ为正则化参数,对于参数b,是否进行惩罚带来的影响很小。
m i n w ⃗ , b { J ( w ⃗ , b ) } = m i n w ⃗ , b { 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 + λ 2 m ∑ j = 1 n w j 2 } \underset{\vec{w},b}{min} \{J(\vec{w},b)\} = \underset{\vec{w},b}{min}\{ \frac{1}{2m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=1}^nw_j^2 \} w,bmin{J(w,b)}=w,bmin{2m1i=1∑m(fw,b(x(i))−y(i))2+2mλj=1∑nwj2}
上式中第一项为均方误差代价(squared error cost),第二项为正则化项(regularization term)。
当 λ \lambda λ取不同值时会有不同的惩罚效果,考虑两个极端情况,若 λ = 0 \lambda=0 λ=0,其实就是不进行惩罚,则可能会产生之前的过拟合现象;若 λ = 1 \lambda=1 λ=1,则对每一项都进行了极大的惩罚,这就使得模型变为: f w ⃗ , b ( x ⃗ ) = b f_{\vec{w},b}(\vec{x}) = b fw,b(x)=b,也就产生了欠拟合情况。
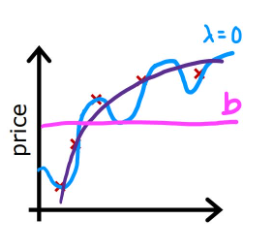
2.5.4 线性回归模型的正则化
根据上文中给出的新模型,可以得出正则化后的梯度下降算法:
r e p e a t { w j = w j − α ∂ ∂ w j J ( w ⃗ , b ) = w j − α [ 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) + λ m w j ] b = b − α ∂ ∂ b J ( w ⃗ , b ) = b − α [ 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ] } s i m u l t a n e o u s u p d a t e s a n d f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b \begin{align} &repeat \{ \\ &\qquad w_j = w_j - α \frac{∂}{∂w_j} J(\vec{w},b) = w_j - α [ \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} + \frac{\lambda}{m}w_j ] \\ &\qquad b = b - α \frac{∂}{∂b} J(\vec{w},b) = b - α [ \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) ] \\ &\} simultaneous \quad updates \\\\ &and \quad f_{\vec{w},b}(\vec{x}) = \vec{w} · \vec{x} + b \end{align} repeat{wj=wj−α∂wj∂J(w,b)=wj−α[m1i=1∑m(fw,b(x(i))−y(i))xj(i)+mλwj]b=b−α∂b∂J(w,b)=b−α[m1i=1∑m(fw,b(x(i))−y(i))]}simultaneousupdatesandfw,b(x)=w⋅x+b
我们可以对上式中关于 w j w_j wj的式子进行简单化简:
w j = w j − α [ 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) + λ m w j ] = w j − α λ m w j − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) = ( 1 − α λ m ) w j − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) \begin{align} w_j &= w_j - α [ \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} + \frac{\lambda}{m}w_j ] \\ &= w_j - α \frac{\lambda}{m} w_j - α \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \\ &= (1 - α \frac{\lambda}{m}) w_j - α \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \\ \end{align} wj=wj−α[m1i=1∑m(fw,b(x(i))−y(i))xj(i)+mλwj]=wj−αmλwj−αm1i=1∑m(fw,b(x(i))−y(i))xj(i)=(1−αmλ)wj−αm1i=1∑m(fw,b(x(i))−y(i))xj(i)
对比之前得到的线性回归模型梯度下降算法中关于 w j w_j wj的式子:
w j = w j − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) w_j = w_j - α \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} wj=wj−αm1i=1∑m(fw,b(x(i))−y(i))xj(i)
不难看出,正则化后的表达式与未正则化的表达式的不同之处在于:第一项之前乘了 ( 1 − α λ m ) (1 - α \frac{\lambda}{m}) (1−αmλ)。
α \alpha α是学习率,是一个很小的正数(0-1), λ \lambda λ是正则化参数,也是一个较小的正数(1-10),m表示一个训练集中的样本数量,通常较大,所以不难算出 ( 1 − α λ m ) (1 - α \frac{\lambda}{m}) (1−αmλ)是一个略微小于1的正数。
这其实就是正则化的工作原理:在每次迭代时主动减小一些 w j w_j wj,然后执行普通更新,所以才使得原本不收敛的学习路线图变得收敛。
2.5.5 逻辑回归模型的正则化
根据逻辑回归模型的代价函数以及前文得到的正则化方法,可以构建新的代价函数:
J ( w ⃗ , b ) = − 1 m ∑ i = 1 m { y ( i ) l o g [ f w ⃗ , b ( x ⃗ ( i ) ) ] + ( 1 − y ( i ) ) l o g [ 1 − f w ⃗ , b ( x ⃗ ( i ) ) ] } + λ 2 m ∑ j = 1 n w j 2 J(\vec{w},b)= -\frac{1}{m} \sum_{i=1}^m \{ \ y^{(i)}log[f_{\vec{w},b}(\vec{x}^{(i)})] +(1-y^{(i)})log[1-f_{\vec{w},b}(\vec{x}^{(i)})] \ \} + \frac{\lambda}{2m} \sum_{j=1}^nw_j^2 J(w,b)=−m1i=1∑m{ y(i)log[fw,b(x(i))]+(1−y(i))log[1−fw,b(x(i))] }+2mλj=1∑nwj2
同样可以得到下面的正则化后的逻辑回归模型的代价函数:
r e p e a t { w j = w j − α ∂ ∂ w j J ( w ⃗ , b ) = ( 1 − α λ m ) w j − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) b = b − α ∂ ∂ b J ( w ⃗ , b ) = b − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) } s i m u l t a n e o u s u p d a t e s a n d f w ⃗ , b ( x ⃗ ) = g ( w ⃗ ⋅ x ⃗ + b ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) \begin{align} &repeat \{ \\ &\qquad w_j = w_j - α \frac{∂}{∂w_j} J(\vec{w},b) = (1 - α \frac{\lambda}{m}) w_j - α \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \\ &\qquad b = b - α \frac{∂}{∂b} J(\vec{w},b) = b - α \frac{1}{m} \sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \\ &\} simultaneous \quad updates \\\\ &and \quad f_{\vec{w},b}(\vec{x}) = g(\vec{w} · \vec{x} + b) = \frac{1}{1 + e^{-(\vec{w} · \vec{x} + b)}} \end{align} repeat{wj=wj−α∂wj∂J(w,b)=(1−αmλ)wj−αm1i=1∑m(fw,b(x(i))−y(i))xj(i)b=b−α∂b∂J(w,b)=b−αm1i=1∑m(fw,b(x(i))−y(i))}simultaneousupdatesandfw,b(x)=g(w⋅x+b)=1+e−(w⋅x+b)1
相关文章:

【Machine Learning】01-Supervised learning
01-Supervised learning 1. 机器学习入门1.1 What is Machine Learning?1.2 Supervised learning1.3 Unsupervised learning 2. Supervised learning2.1 单元线性回归模型2.1.1 Linear Regression Model(线性回归模型)2.1.2 Cost Function(代…...

《视觉 SLAM 十四讲》V2 第 8 讲 视觉里程计2 【如何根据图像 估计 相机运动】【光流 —> 直接法】
OpenCV关于 光流的教程 文章目录 第 8 讲 视觉里程计 28.2 光流8.3 实践: LK 光流 【Code】本讲 CMakeLists.txt 8.4 直接法8.5 实践: 双目的稀疏直接法 【Code】8.5.4 直接法的优缺点 习题 8√ 题1 光流方法题2题3题4题5 第 8 讲 视觉里程计 2 P205 …...

Unity DOTS System与SystemGroup概述
最近DOTS终于发布了正式的版本, 我们来分享以下DOTS里面System关键概念,方便大家上手学习掌握Unity DOTS开发。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀! System是迭代计算与处理World中的…...
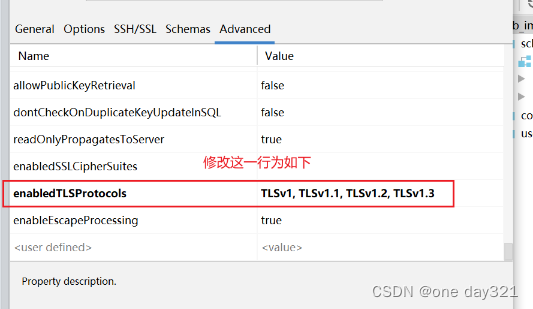
IDEA使用内置database数据库连接mysql报错:javax.net.ssl.SSLHandshakeException
参考一些博客的方式: 使用idea内置database连接数据库报错javax.net.ssl.SSLHandshakeException: No appropriate protocol_idea database ssl_你当像山的博客-CSDN博客 他们的方式是:在url后添加useSSLfalse 介绍另外一种方式: 点击datab…...

从Flink的Kafka消费者看算子联合列表状态的使用
背景 算子的联合列表状态是平时使用的比较少的一种状态,本文通过kafka的消费者实现来看一下怎么使用算子列表联合状态 算子联合列表状态 首先我们看一下算子联合列表状态的在进行故障恢复或者从某个保存点进行扩缩容启动应用时状态的恢复情况 算子联合列表状态主…...

CSS3 按钮
创建 CSS3 按钮可以通过组合样式属性和伪类来实现 <!DOCTYPE html> <html> <head><link rel"stylesheet" type"text/css" href"styles.css"> </head> <body><button class"basic-button">…...
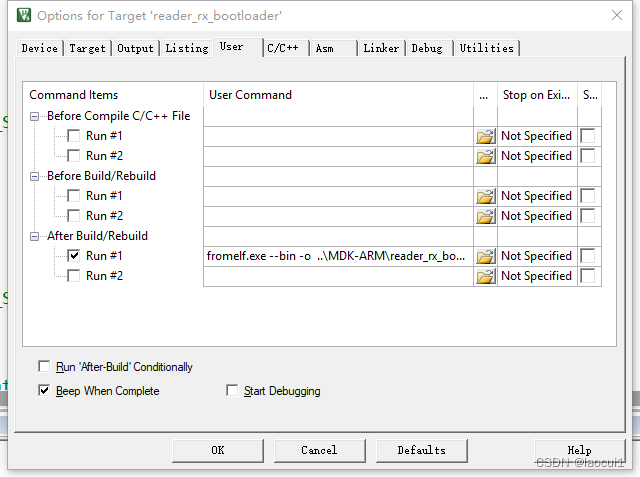
STM32 BootLoader设置
编写bootloader程序: 直接复制下面代码到自己程序中。 typedef void (*iapfun)(void); //定义一个函数类型的参数. iapfun jump2app; //设置栈顶地址 //addr:栈顶地址 __asm void MSR_MSP(u32 addr) {MSR MSP, r0 //set Main Stack valueBX r14 }//跳转到…...

django REST framework-使用与不使用的区别?
首先,来回顾一下传统的基于模板引擎的 django 开发工作流: 绑定 URL 和视图函数。当用户访问某个 URL 时,调用绑定的视图函数进行处理。 编写视图函数的逻辑。视图中通常涉及数据库的操作。 在视图中渲染 HTML 模板,返回 HTTP 响应…...

获取URL中的参数
获取URL中的参数 function getUrlParam(name) {var reg new RegExp("(^|&)" name "([^&]*)(&|$)");var r window.location.search.substr(1).match(reg);if (r ! null)return unescape(r[2]);return null; } 这个正则表达式就是一个URL路…...
一起学数据结构(9)——二叉树的链式存储及相关功能实现
目录 1. 二叉树的链式存储: 2. 二叉树的前序遍历: 3. 二叉树的中序遍历: 4. 二叉树的后序遍历: 5. 统计二叉树的结点总数 6.统计二叉树的叶子结点数: 7. 统计二叉树第层的结点数量: 8. 二叉树的销毁…...

vue 后端返回二进制流-前端通过blob对象下载文件-图片
前言 在实际开发中我们经常会遇见下载文件的场景,比如下载合同,下载文件 下载文件有2种方式,一种是后端返回二进制流,前端通过blob对象接受根据不同类型下载 还有一种把地址直接在浏览器新窗口打开浏览器打开pdf可以预览和下载&…...
)
vue el-dialog封装成子组件(组件化)
前言 实际开发过程中我们经常听见组件化开发,但在实际开发过程中(没有人审查时)怎么方便来 我们有时是因为时间不够,所以把所有代码写在一个页面。当业务逻辑复杂时可能会有1k多行 虽然不能要求自己写出高效复用性高的组件&…...

爬虫教程 一 requests包的使用
request 简介 requests 是一个常用的 HTTP 请求库,可以方便地向网站发送 HTTP 请求,并获取响应结果。 response.text 和response.content的区别 response.text 类型:str解码类型: requests模块自动根据HTTP 头部对响应的编码作…...
Aria2NG连接aria2-pro提示认证失败的处理办法
本文档适用于已经安装了aria2-pro和AriaNg的小伙伴~ 第一次登录管理端会提示”认证失败“ 这是因为aria设置了密码,需要在设置中配置上密码即可 配置完密码重新加载就可以正常使用啦 下载速度明显比以前快了很多 下载参考文档 Docker安装下载神器aria2并使用过程记…...
MYSQL 连接
高频 SQL 50 题(基础版) - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台 1378. 使用唯一标识码替换员工ID SELECT COALESCE(unique_id, NULL) AS unique_id,name FROM Employees LEFT JOIN EmployeeUNI ON Employees.…...

SeaTunnel 换maven源,解决插件下载慢
SeaTunnel 是使用的mvnw命令,可以先执行一下install-plugin.sh然后终止 理论上应该可以直接执行mvnw,他就会去安装下载maven,目录就是下面的目录 然后去服务器目录修改 setting.xml文件,设置镜像源即可 /root/.m2/wrapper/dists/apache-maven-3.8.4-bin/52ccbt68d252mdldqsfsn…...
安卓14通过“冻结”缓存应用程序腾出CPU,提高性能和内存效率
本月早些时候,我们听说更新到安卓14似乎提高了谷歌Pixel 7和Pixel 6的效率——提高了电池寿命,并在这个过程中减少了热量的产生。现在看来,安卓14的增效功能细节已经公布。 安卓侦探Mishaal Rahman在X(前身为Twitter)…...

jupyter崩溃OOM,out of memory,jupyter代码写不进去,保存不了。
最近写一个比较长的数据处理代码,有快千行,然后经常代码没有写入,然后直接网页崩溃,给我干蒙了。我已经是jupyter版本的问题,弄了半天,弄完,还是有这个问题。然后就查了一下,发现是j…...
一文带你快速掌握爬虫开发中的一些高级调试技巧
文章目录 1. 写在前面2. Reply XHR(重新发起请求)3. copy as fecth(修改参数请求)4. copy()复制变量5. Web网页全屏截图6. 控制台安装使用npm7. 控制台中引用上次执行结果8. 控制台表展示对象数组 1. 写在前面 做过爬虫开发的人都…...

6.(vue3.x+vite)路由传参query与params区别
前端技术社区总目录(订阅之前请先查看该博客) 效果截图 一:路由传参有两种方式:params与query params与query区别 1:param,路由带“/”,query带“?” 2:query传过来的参数会显示到地址栏中 而params传过来的参数可以显示参数或隐藏参数到地址栏中(vue-router 4.1.4不…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
