[蓝桥杯 2022 省 B] 统计子矩阵
题目描述
给定一个 N×M 的矩阵 A,请你统计有多少个子矩阵 (最小 1×1, 最大 N×M) 满足子矩阵中所有数的和不超过给定的整数 K。
输入格式
第一行包含三个整数 N, M和 K。
之后 N 行每行包含 M 个整数, 代表矩阵 A。
输出格式
一个整数代表答案。
输入输出样例
输入 #1
3 4 10 1 2 3 4 5 6 7 8 9 10 11 12输出 #1
19说明/提示
【样例说明】
满足条件的子矩阵一共有 19,包含:
大小为 1×1 的有 10个。
大小为1×2 的有 3 个。 大小为1×3 的有 2 个。
大小为 1×4 的有 1 个。
大小为 2×1 的有 3 个。
【评测用例规模与约定】
对于30% 的数据, N,M≤20.
对于 70% 的数据, N,M≤100.
对于 100% 的数据, 1≤N,M≤500,0≤Aij≤1000,1≤K≤2.5×10^8.
蓝桥杯 2022 省赛 B 组 F 题。
80代码 O(n^4)
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=1e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
int qsm(int x,int n)
{int res=1;while(n){if(n&1)res=res*x%mod;x=x*x%mod;n>>=1;} return res;
}
int n,m,k;
int a[510][510];
int sum[510][510];
signed main()
{cin>>n>>m>>k;fp(i,1,n){fp(j,1,m){cin>>a[i][j];sum[i][j]=sum[i][j-1]+sum[i-1][j]+a[i][j]-sum[i-1][j-1];}}int cnt=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){for(int t=i;t<=n;t++){for(int f=j;f<=m;f++){int x=sum[t][f]-sum[i-1][f]-sum[t][j-1]+sum[i-1][j-1];if(x<=k)cnt++;}}}}cout<<cnt<<"\n";return 0;
} 100代码O(n^3)
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=1e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
int qsm(int x,int n)
{int res=1;while(n){if(n&1)res=res*x%mod;x=x*x%mod;n>>=1;} return res;
}
int n,m,k;
int a[510][510];
int sum[510][510];
signed main()
{cin>>n>>m>>k;fp(i,1,n){fp(j,1,m){cin>>a[i][j];sum[i][j]=sum[i-1][j]+a[i][j];}}int cnt=0;for(int i=1;i<=n;i++){for(int j=i;j<=n;j++){int s=0;for(int l=1,r=1;r<=m;r++){s+=sum[j][r]-sum[i-1][r];while(s>k){s-=sum[j][l]-sum[i-1][l];l++;}cnt+=r-l+1;}}}cout<<cnt<<"\n";return 0;
} 相关文章:

[蓝桥杯 2022 省 B] 统计子矩阵
题目描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵 (最小 11, 最大 NM) 满足子矩阵中所有数的和不超过给定的整数 K。 输入格式 第一行包含三个整数 N, M和 K。 之后 N 行每行包含 M 个整数, 代表矩阵 A。 输出格式 一个整数代表答案。 输入输出样例 输入 #1 3…...

解决在部署springboot项目的docker中执行备份与之相连接的mysql容器命令
文章目录 问题描述解决思路问题解决容器构建mysql客户端安装容器与主机的交互docker中执行 mysqldump 命令解决mysql8密码验证问题解决密码插件警告 问题描述 由于,使用1panel可视化的面板来部署springboot项目,可以很方便地安装和使用mysql,…...

正文Delphi XE Android下让TMemo不自动弹出键盘
用TMemo来显示一段说明文字,可一点Memo,就弹出键盘,找了半天控制键盘的属性,没找到。最后将readOnly设置为True搞定。 如果需要一个form都不显示keyboard,那么可以利用全局变量 VKAutoShowMode来控制,这个全局变量可以有下面三个值…...

[1Panel]开源,现代化,新一代的 Linux 服务器运维管理面板
测评介绍 本期测评试用一下1Panel这款面板。1Panel是国内飞致云旗下开源产品。整个界面简洁清爽,后端使用GO开发,前端使用VUE的Element-Plus作为UI框架,整个面板的管理都是基于docker的,想法很先进。官方还提供了视频的使用教程&…...
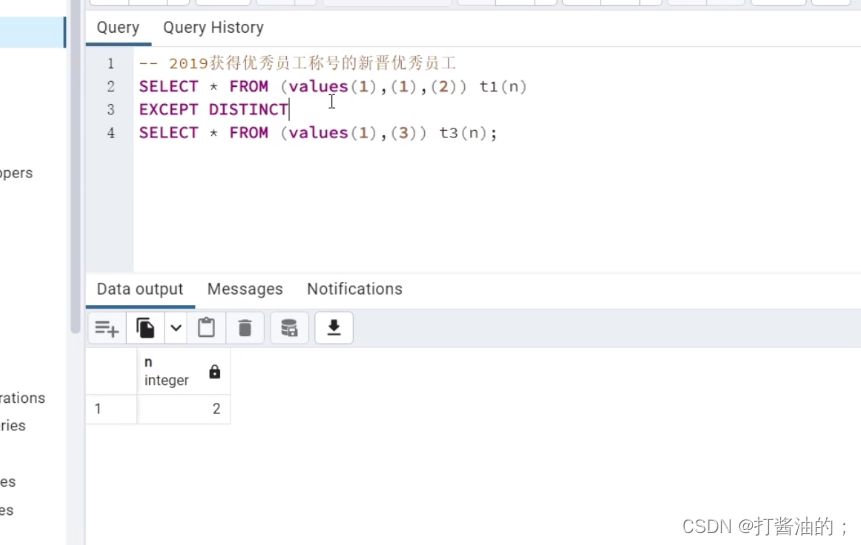
PG集合查询
1.运算符 1.1 union并集 连接上下语句 union distinct连接并且去重 all不去重 1.2 intersect交集 上下交集 distinct连接并且去重 all不去重 1.3 except除外 上面除了下面 distinc去重 all不去重...
目标检测应用场景和发展趋势
参考: 目标检测的未来是什么? - 知乎 (zhihu.com)https://www.zhihu.com/question/394900756/answer/32489649815大应用场景 1 行人检测: 遮挡问题:行人之间的互动和遮挡是非常常见的,这给行人检测带来了挑战。非刚性…...
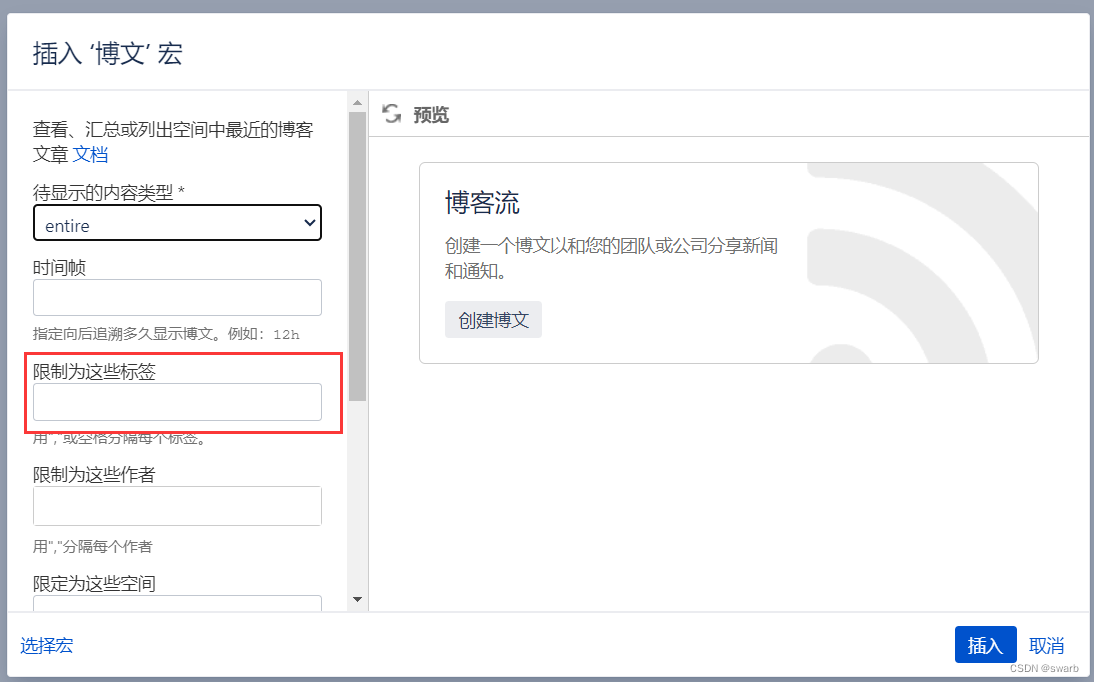
Confluence 自定义博文列表
1. 概述 Confluence 自有博文列表无法实现列表自定义功能,实现该需求可采用页面中引用博文宏标签控制的方式 2. 实现方式 功能入口: Confluence →指定空间→创建页面 功能说明: (1)页面引用博文宏 (…...

chrome历史版本下载
chrome历史版本下载 windows Google Chrome all versions on Windows linux版本 Google Chrome 64bit Linux版_chrome浏览器,chrome插件,谷歌浏览器下载,谈笑有鸿儒...
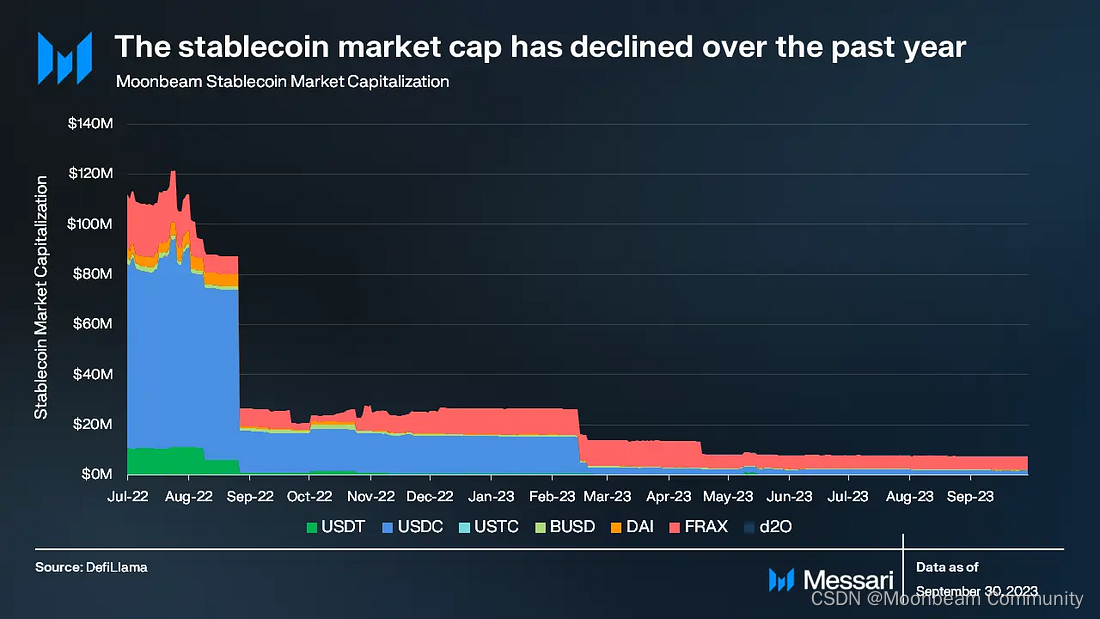
Messari发布Moonbeam简报,每日交易量稳步增长,首次公布利润数据
区块链数据公司Messari首次发布Moonbeam项目分析简报,从项目市值、链上数据表现、质押以及Moonbeam的技术优势XCM使用量等角度全面分析。这个再熊市初期上线的项目一直在默默开发,并在跨链互操作领域拥有了相当的实操成绩。我们翻译了Messari简报中的部分…...

数据库 锁、索引、在实际开发中怎么设置和优化
数据库锁和索引是数据库管理的两个重要方面,它们对于确保数据的一致性和提高查询性能具有重要作用。在实际开发中,正确地设置和优化锁和索引对于构建高效、稳定的系统至关重要。下面是一些关于如何在实际开发中设置和优化锁和索引的建议: 锁…...
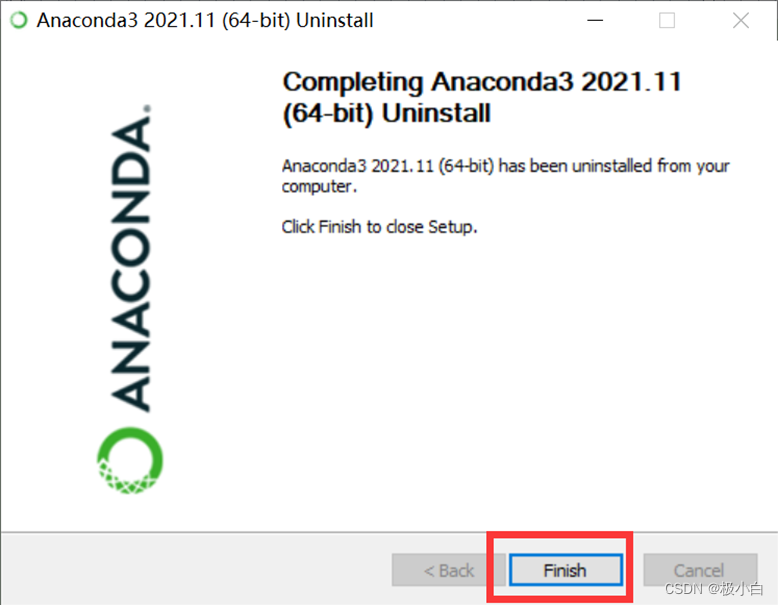
超详细彻底卸载Anaconda详细教程
一、在开始处打开Anaconda Prompt 二、打开后,输入conda install tqdm -f命令并按回车键 conda install tqdm -f三、之后页面会出现一个WANNING,这个我们不用在意,然后会出现一个y/n提示框,在这里我们输入y或者Y y四、输入cond…...
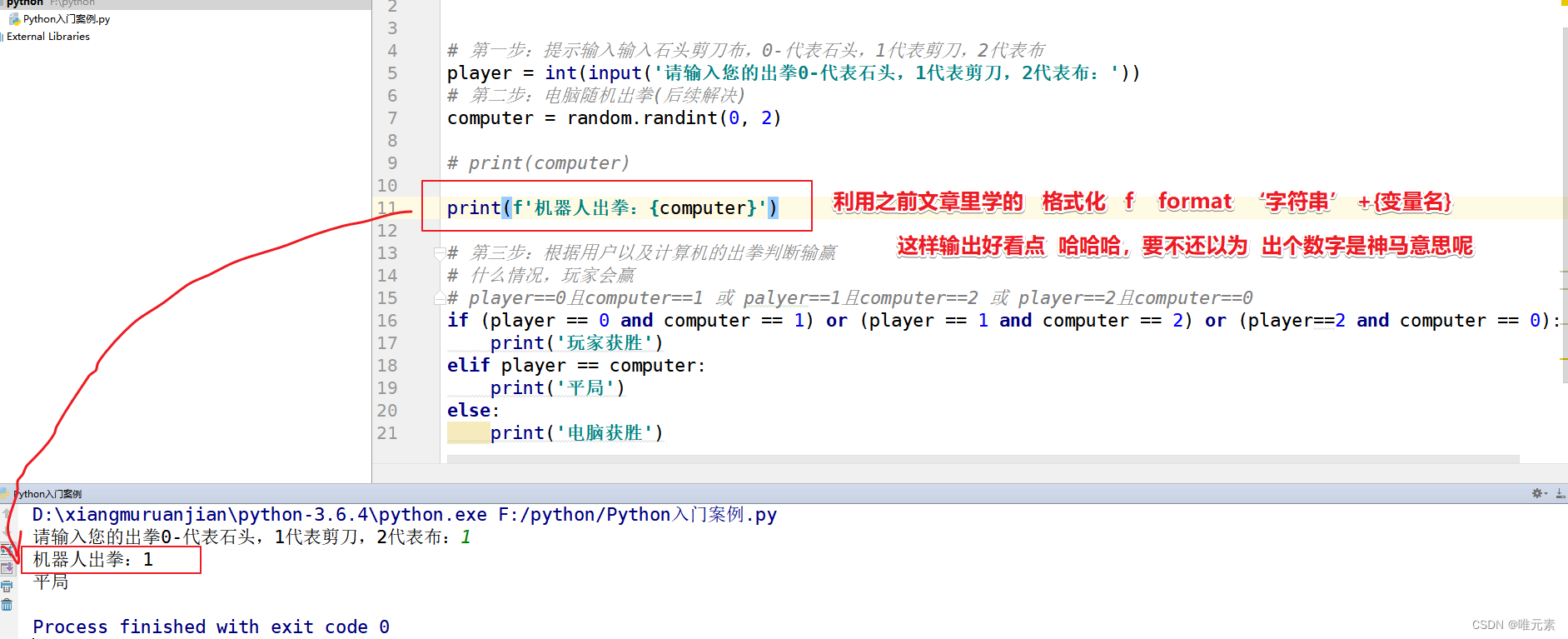
Python--随机出拳(random)--if判断--综合案例练习:石头剪刀布
注:涉及相关链接: Python:if判断--综合案例练习:石头剪刀布-CSDN博客 Python语言非常的强大,强大之处就在于其拥有很多模块(module),这些模块中拥有很多别人已经开发好的代码&…...

微信小程序里配置less
介绍 在微信小程序里,样式文件的后缀名都是wxss,这导致一个问题,就是页面样式过多的时候,要写很多的类名来包裹,加大了工作量,还很有可能会写错样式。这时可以配置一个less,会大大提高代码编辑…...
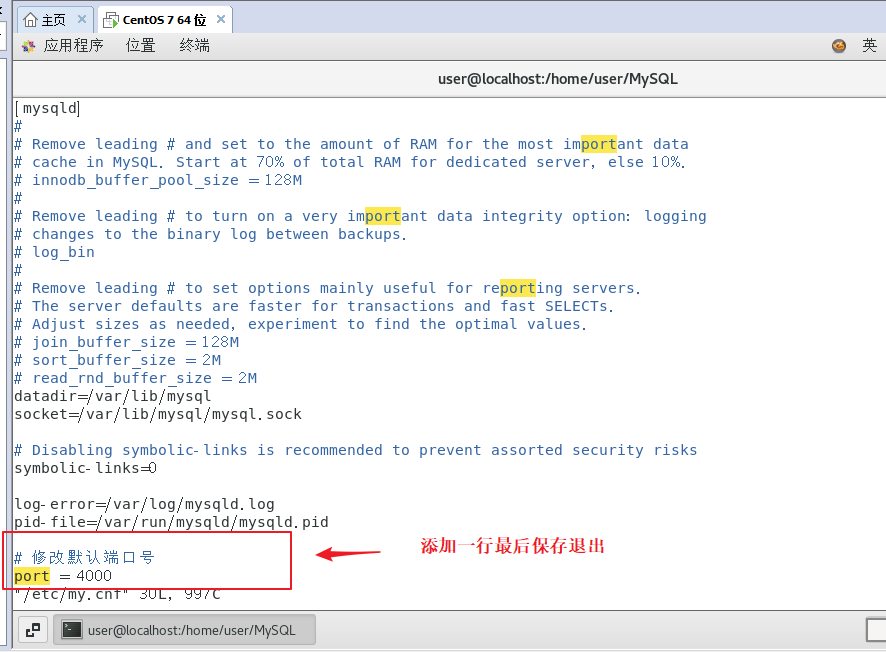
MySq修改配置文件
要修改 MySQL 的配置文件,您可以按照以下步骤进行操作: 1、打开 MySQL 的配置文件 在大多数 Linux 系统上,默认的配置文件路径是 /etc/my.cnf 或 /etc/mysql/my.cnf。您可以使用文本编辑器(如 vim、nano)以管理员权限打开该文件。 sudo vim /etc/my.cnf 2、进行修改 …...
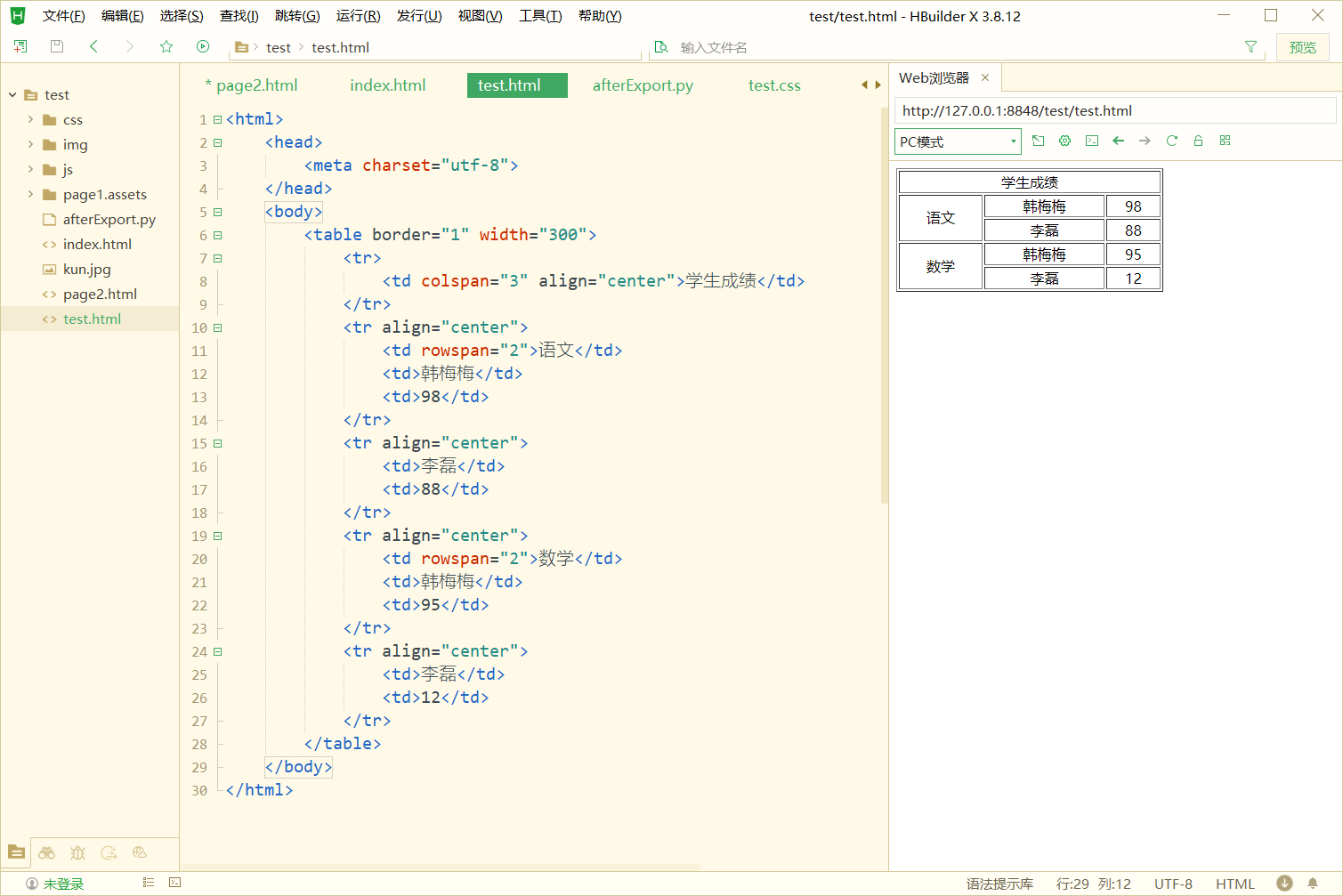
HTML 表格及练习
表格 概述 表格是一种二维结构,横行纵列。 由单元格组成。 表格是一种非常“强” 的结构: 每一行有相同的列数(单元格),每一列有相同的行数(单元格) 同一列的单元格,宽度&#…...
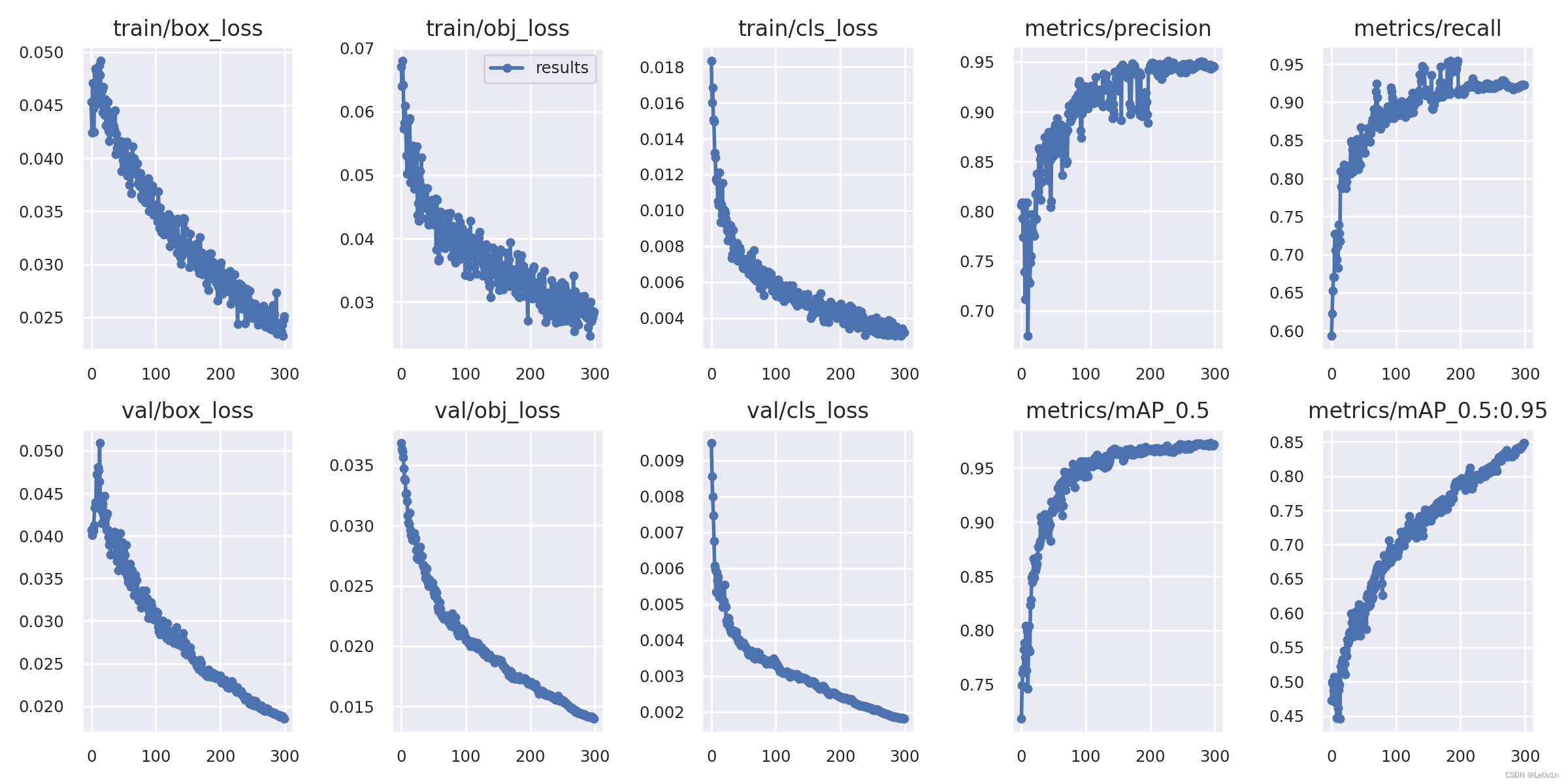
YOLOv5-训练自己的VOC格式数据集(VOC、自建数据集)
YOLOv5:训练自己的 VOC 格式数据集 1. 自定义数据集 1.1 环境安装 pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple注意: 安装 lxmlPillow 版本要低于 10.0.0,解释链接: module ‘PIL.Image’ has no attri…...
基于Java的考研信息查询系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding) 代码参考数据库参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者&am…...

Linux性能优化--性能追踪:受CPU限制的应用程序(GIMP)
10.0 概述 本章包含了一个例子:如何用Linux性能工具在受CPU限制的应用程序中寻找并修复性能问题。 阅读本章后,你将能够: 在受CPU限制的应用程序中明确所有的CPU被哪些源代码行使用。用1trace和oprofile弄清楚应用程序调用各种内部与外部函…...
BERT变体(1):ALBERT、RoBERTa、ELECTRA、SpanBERT
Author:龙箬 Computer Application Technology Change the World with Data and Artificial Intelligence ! CSDNweixin_43975035 *天下之大,虽离家万里,何处不可往!何事不可为! 1. ALBERT \qquad ALBERT的英文全称为A Lite versi…...
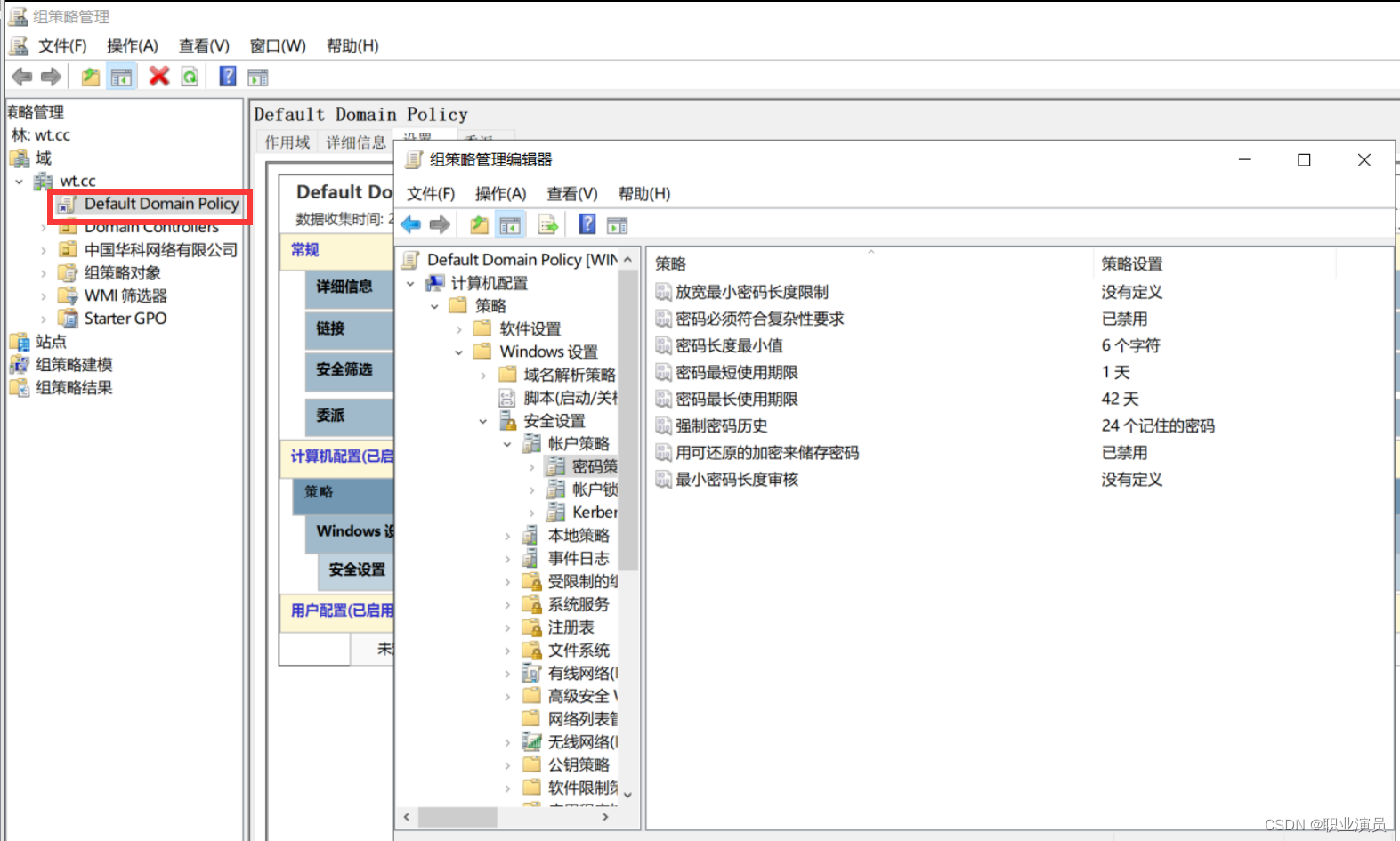
域控操作二:设置域用户使用简单密码
过程太多简单 直接写出路径更改即可 组策略—计算机配置----策略—Windows设置–安全设置----账户策略–密码策略 按自己想法改就行了 注意一点!!!!! 要么自己设置策略,要么从默认策略改!&am…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
