机器学习基础之《回归与聚类算法(3)—线性回归优化:岭回归》
一、什么是岭回归
其实岭回归就是带L2正则化的线性回归
岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上L2正则化的限制,从而达到解决过拟合的效果
二、API
1、sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, solver="auto", normalize=False)
具有l2正则化的线性回归
alpha:正则化力度=惩罚项系数,也叫λ
λ取值:0~1或1~10
fit_intercept:是否添加偏置
solver:会根据数据自动选择优化方法
sag:如果数据集、特征都比较大,会自动选择sag这个随机梯度下降优化
normalize:数据是否进行标准化
normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
normalize=True:在预估器流程前会自动做标准化
Ridge.coef_:回归权重
Ridge.intercept_:回归偏置
2、Ridge方法相当于SGDRegressor(penalty='l2', loss="squared_loss"),只不过SGDRegressor实现了一个普通的随机梯度下降学习,推荐使用Ridge(实现了SAG)
penalty:可以是l1或l2,这里是给线性回归加上L2惩罚项
3、sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)
加上了交叉验证的岭回归
具有l2正则化的线性回归,可以进行交叉验证
coef_:回归系数
三、正则化力度(惩罚项系数)对最终结果有什么影响
1、惩罚项系数是上面的λ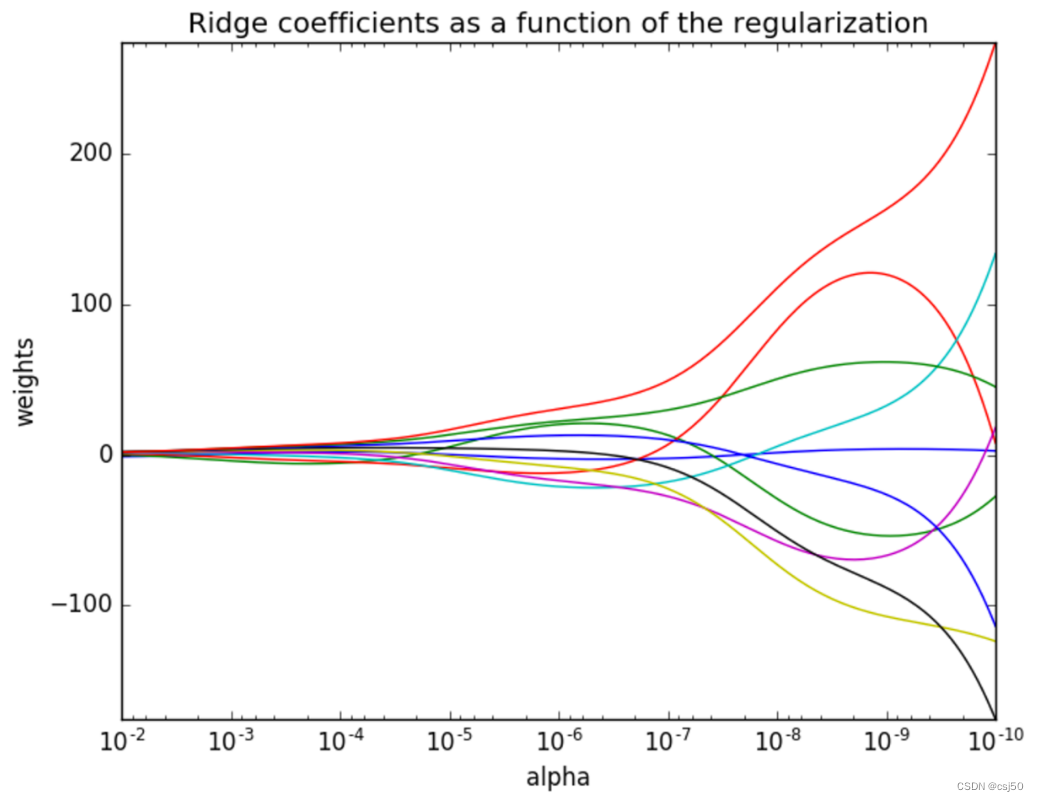
横坐标是正则化力度,也就是alpha。纵坐标是权重系数
正则化力度越大(向左),权重系数会越小(接近于0)
正则化力度越小(向右),权重系数会越大
四、波士顿房价预测
1、修改day03_machine_learning.py
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_errordef linear1():"""正规方程的优化方法对波士顿房价进行预测"""# 1、获取数据boston = load_boston()# 2、划分数据集x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)# 3、标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4、预估器estimator = LinearRegression()estimator.fit(x_train, y_train)# 5、得出模型print("正规方程-权重系数为:\n", estimator.coef_)print("正规方程-偏置为:\n", estimator.intercept_)# 6、模型评估y_predict = estimator.predict(x_test)print("预测房价:\n", y_predict)error = mean_squared_error(y_test, y_predict)print("正规方程-均方误差为:\n", error)return Nonedef linear2():"""梯度下降的优化方法对波士顿房价进行预测"""# 1、获取数据boston = load_boston()# 2、划分数据集x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)# 3、标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4、预估器estimator = SGDRegressor()estimator.fit(x_train, y_train)# 5、得出模型print("梯度下降-权重系数为:\n", estimator.coef_)print("梯度下降-偏置为:\n", estimator.intercept_)# 6、模型评估y_predict = estimator.predict(x_test)print("预测房价:\n", y_predict)error = mean_squared_error(y_test, y_predict)print("梯度下降-均方误差为:\n", error)return Nonedef linear3():"""岭回归对波士顿房价进行预测"""# 1、获取数据boston = load_boston()# 2、划分数据集x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)# 3、标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4、预估器estimator = Ridge()estimator.fit(x_train, y_train)# 5、得出模型print("岭回归-权重系数为:\n", estimator.coef_)print("岭回归-偏置为:\n", estimator.intercept_)# 6、模型评估y_predict = estimator.predict(x_test)print("预测房价:\n", y_predict)error = mean_squared_error(y_test, y_predict)print("岭回归-均方误差为:\n", error)return Noneif __name__ == "__main__":# 代码1:正规方程的优化方法对波士顿房价进行预测linear1()# 代码2:梯度下降的优化方法对波士顿房价进行预测linear2()# 代码3:岭回归对波士顿房价进行预测linear3()
2、运行结果
正规方程-权重系数为:[-1.16537843 1.38465289 -0.11434012 0.30184283 -1.80888677 2.341711660.32381052 -3.12165806 2.61116292 -2.10444862 -1.80820193 1.19593811-3.81445728]
正规方程-偏置为:21.93377308707127
预测房价:[31.11439635 31.82060232 30.55620556 22.44042081 18.80398782 16.2762532236.13534369 14.62463338 24.56196194 37.27961695 21.29108382 30.6125824127.94888799 33.80697059 33.25072336 40.77177784 24.3173198 23.2977324125.50732006 21.08959787 32.79810915 17.7713081 25.36693209 25.0381105932.51925813 20.4761305 19.69609206 16.93696274 38.25660623 0.7015249932.34837791 32.21000333 25.78226319 23.95722044 20.51116476 19.537272583.87253095 34.74724529 26.92200788 27.63770031 34.47281616 29.8051127118.34867051 31.37976427 18.14935849 28.22386149 19.25418441 21.7149039538.26297011 16.44688057 24.60894426 19.48346848 24.49571194 34.4891563526.66802508 34.83940131 20.91913534 19.60460332 18.52442576 25.0017879919.86388846 23.46800342 39.56482623 42.95337289 30.34352231 16.893355923.88883179 3.33024647 31.45069577 29.07022919 18.42067822 27.4431489719.55119898 24.73011317 24.95642414 10.36029002 39.21517151 8.3074326218.44876989 30.31317974 22.97029822 21.0205003 19.99376338 28.647549730.88848414 28.14940191 26.57861905 31.48800196 22.25923033 -5.3597325221.66621648 19.87813555 25.12178903 23.51625356 19.23810222 19.046423427.32772709 21.92881244 26.69673066 23.25557504 23.99768158 19.2845825921.19223276 10.81102345 13.92128907 20.8630077 23.40446936 13.9168948428.87063386 15.44225147 15.60748235 22.23483962 26.57538077 28.6420362324.16653911 18.40152087 15.94542775 17.42324084 15.6543375 21.0413626433.21787487 30.18724256 20.92809799 13.65283665 16.19202962 29.2515560313.28333127]
正规方程-均方误差为:32.44253669600673
梯度下降-权重系数为:[-1.10819189 1.24846017 -0.33692976 0.35488997 -1.5988338 2.497786120.23532503 -2.95918503 1.78713201 -1.30658932 -1.7651645 1.22848984-3.78378732]
梯度下降-偏置为:[21.9372382]
预测房价:[30.55704932 32.05173832 30.60725341 23.44937757 18.99917813 16.1000257536.35984687 14.8219597 24.40027383 37.32474782 21.5136228 30.6786441827.64263953 33.58715018 33.34357549 41.02961052 24.56190835 22.826545725.55091571 21.70092286 32.87467814 17.66098552 25.68694993 25.1525498533.16850623 20.32656198 19.71924549 16.85013083 38.36906677 -0.063612532.73406521 32.08051235 26.11082213 24.04506778 20.25729015 19.777164693.70619504 34.45691833 26.92882569 27.80690875 34.66542721 29.5705631918.17563119 31.52879095 17.99350098 28.56441014 19.19066091 21.4221363238.1145129 16.56749119 24.53862046 19.30611604 24.18857419 35.0850191926.86672187 34.85386528 21.23005703 19.56549835 18.32581965 25.0223145420.21024376 23.85118373 40.23475025 43.25772524 30.50012791 17.1749763623.97539731 2.78651333 31.14016986 29.84080487 18.33899648 27.4617082719.28192918 24.53788739 25.36787612 10.25023757 39.41179243 7.9710262818.11455433 30.92992358 22.98914795 21.89678026 20.29065302 28.5543570831.1738028 28.36545081 26.50764708 31.89860003 22.31334327 -5.7728714921.72210665 19.74247295 25.14530383 23.69494522 18.83967629 19.1579255427.3208327 22.03369451 26.56809141 23.54003515 23.94824339 19.4946140121.04641077 9.8365073 13.99736749 21.15777556 23.16210392 15.1980546828.94748286 15.82614487 15.49056654 21.98524785 27.04398453 28.7181679624.00103595 18.26483509 15.80645364 17.68948585 15.8560435 20.7547522933.18483916 30.80830718 21.1511169 14.13781488 16.30748901 29.1982781413.02414535]
梯度下降-均方误差为:32.589364375873274
岭回归-权重系数为:[-1.15338693 1.36377246 -0.13566076 0.30685046 -1.77429221 2.35657730.31109246 -3.08360389 2.51865451 -2.02086382 -1.79863992 1.19474755-3.79397362]
岭回归-偏置为:21.93377308707127
预测房价:[31.02182904 31.81762296 30.5307756 22.56101986 18.83367243 16.2772061636.11020039 14.65795076 24.53401701 37.23901719 21.30179513 30.5929445527.88884922 33.74220094 33.22724169 40.75065038 24.34249271 23.2334033225.49591227 21.16642876 32.76426793 17.77262939 25.375461 25.0421619732.55916012 20.46991441 19.71767638 16.94589789 38.22924617 0.6794581532.36570422 32.16246666 25.81396987 23.96859847 20.48378122 19.562226923.92363179 34.6745904 26.8972682 27.62853379 34.46087333 29.7505016518.3389973 31.36674393 18.1533717 28.23955372 19.25477732 21.6743993838.20456951 16.47703009 24.58448733 19.46850857 24.45078345 34.5144544526.66775912 34.80353844 20.94272686 19.60603364 18.50096422 24.9938738619.89923157 23.49308585 39.58682259 42.93017524 30.32881249 16.930963123.89113672 3.3223193 31.37851848 29.1623479 18.42211411 27.4382901119.52539153 24.68355681 24.98105953 10.39357796 39.19016669 8.3112177518.43234108 30.3568052 22.97522145 21.12688558 20.03476147 28.6193767930.88518359 28.14590934 26.56509999 31.51187089 22.27686749 -5.3124194821.68661135 19.86726981 25.1163169 23.53556822 19.21105599 19.0843777227.30869525 21.94344682 26.65541972 23.26883666 23.9958039 19.3060780621.18985411 10.71242971 13.95709927 20.89648522 23.36054449 14.0580326528.85147775 15.51591674 15.61567092 22.20129229 26.6018834 28.6319077524.13317802 18.39685365 15.94882155 17.46607437 15.7003571 21.004634133.16362767 30.23909552 20.94330259 13.73934571 16.22231382 29.2129078713.28412904]
岭回归-均方误差为:32.4536692771621相关文章:

机器学习基础之《回归与聚类算法(3)—线性回归优化:岭回归》
一、什么是岭回归 其实岭回归就是带L2正则化的线性回归 岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上L2正则化的限制,从而达到解决过拟合的效果 二、API 1、sklearn.linear_model.Ridge(alpha1.0, fit_interceptTrue…...
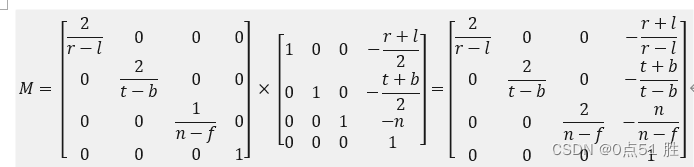
DirectX3D 正交投影学习记录
所谓正交投影变换,就是已知盒状可视空间内任意点坐标(x,y,z),求解垂直投影到xy平面的对应点坐标。 按照这个定义,xyz坐标系本身就是正交坐标系,盒状可视空间内任意点的坐标(x,y,z)投影到(x,y)平面,只要简单地丢弃z坐标…...
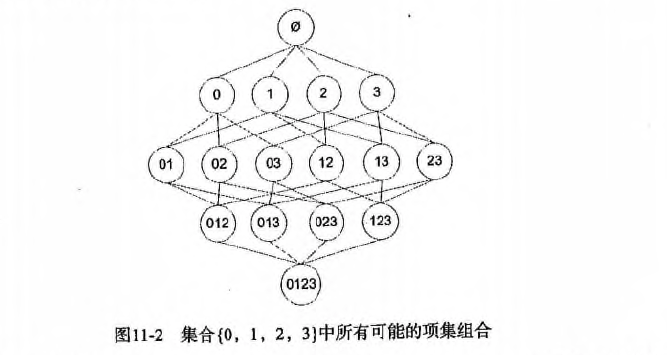
数据挖掘十大算法--Apriori算法
一、Apriori 算法概述 Apriori 算法是一种用于关联规则挖掘的经典算法。它用于在大规模数据集中发现频繁项集,进而生成关联规则。关联规则揭示了数据集中项之间的关联关系,常被用于市场篮分析、推荐系统等应用。 以下是 Apriori 算法的基本概述&#x…...

[蓝桥杯 2022 省 B] 统计子矩阵
题目描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵 (最小 11, 最大 NM) 满足子矩阵中所有数的和不超过给定的整数 K。 输入格式 第一行包含三个整数 N, M和 K。 之后 N 行每行包含 M 个整数, 代表矩阵 A。 输出格式 一个整数代表答案。 输入输出样例 输入 #1 3…...

解决在部署springboot项目的docker中执行备份与之相连接的mysql容器命令
文章目录 问题描述解决思路问题解决容器构建mysql客户端安装容器与主机的交互docker中执行 mysqldump 命令解决mysql8密码验证问题解决密码插件警告 问题描述 由于,使用1panel可视化的面板来部署springboot项目,可以很方便地安装和使用mysql,…...

正文Delphi XE Android下让TMemo不自动弹出键盘
用TMemo来显示一段说明文字,可一点Memo,就弹出键盘,找了半天控制键盘的属性,没找到。最后将readOnly设置为True搞定。 如果需要一个form都不显示keyboard,那么可以利用全局变量 VKAutoShowMode来控制,这个全局变量可以有下面三个值…...

[1Panel]开源,现代化,新一代的 Linux 服务器运维管理面板
测评介绍 本期测评试用一下1Panel这款面板。1Panel是国内飞致云旗下开源产品。整个界面简洁清爽,后端使用GO开发,前端使用VUE的Element-Plus作为UI框架,整个面板的管理都是基于docker的,想法很先进。官方还提供了视频的使用教程&…...
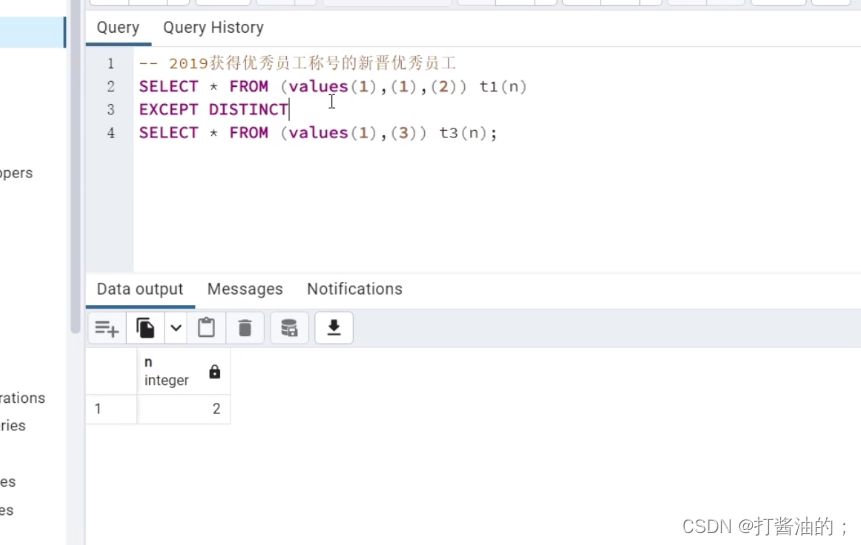
PG集合查询
1.运算符 1.1 union并集 连接上下语句 union distinct连接并且去重 all不去重 1.2 intersect交集 上下交集 distinct连接并且去重 all不去重 1.3 except除外 上面除了下面 distinc去重 all不去重...
目标检测应用场景和发展趋势
参考: 目标检测的未来是什么? - 知乎 (zhihu.com)https://www.zhihu.com/question/394900756/answer/32489649815大应用场景 1 行人检测: 遮挡问题:行人之间的互动和遮挡是非常常见的,这给行人检测带来了挑战。非刚性…...
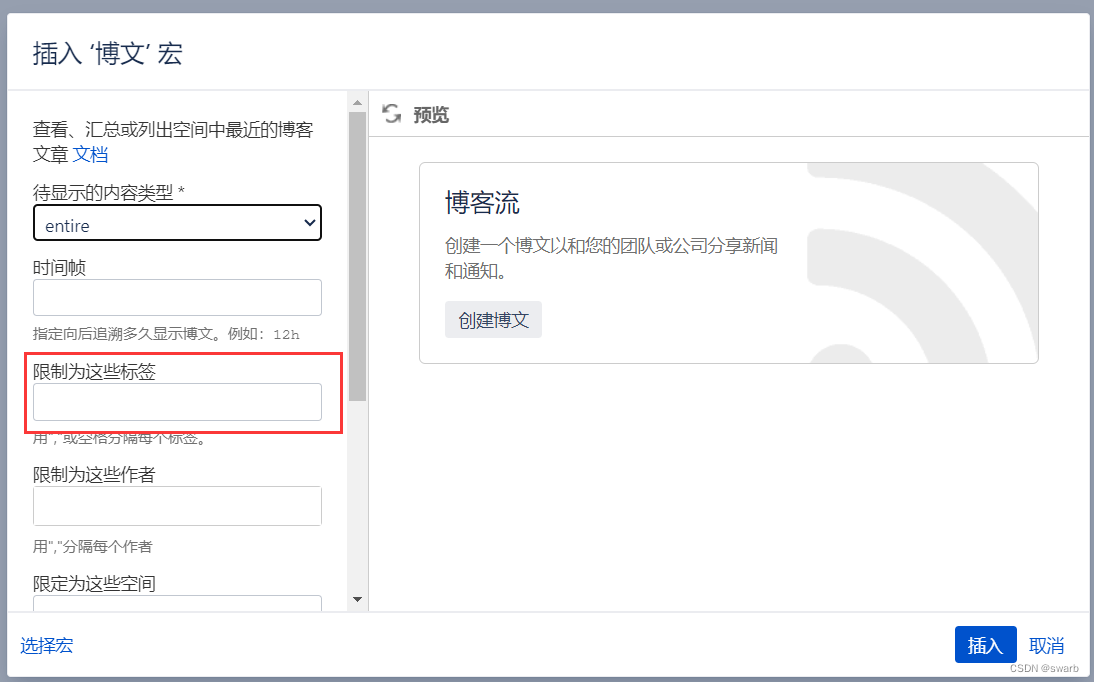
Confluence 自定义博文列表
1. 概述 Confluence 自有博文列表无法实现列表自定义功能,实现该需求可采用页面中引用博文宏标签控制的方式 2. 实现方式 功能入口: Confluence →指定空间→创建页面 功能说明: (1)页面引用博文宏 (…...

chrome历史版本下载
chrome历史版本下载 windows Google Chrome all versions on Windows linux版本 Google Chrome 64bit Linux版_chrome浏览器,chrome插件,谷歌浏览器下载,谈笑有鸿儒...
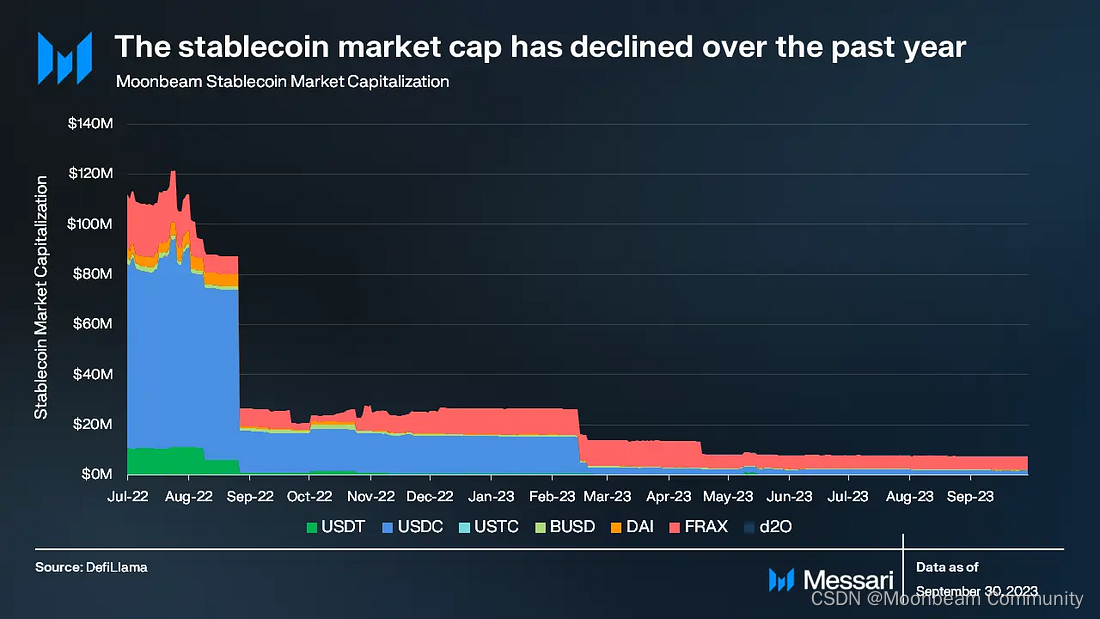
Messari发布Moonbeam简报,每日交易量稳步增长,首次公布利润数据
区块链数据公司Messari首次发布Moonbeam项目分析简报,从项目市值、链上数据表现、质押以及Moonbeam的技术优势XCM使用量等角度全面分析。这个再熊市初期上线的项目一直在默默开发,并在跨链互操作领域拥有了相当的实操成绩。我们翻译了Messari简报中的部分…...

数据库 锁、索引、在实际开发中怎么设置和优化
数据库锁和索引是数据库管理的两个重要方面,它们对于确保数据的一致性和提高查询性能具有重要作用。在实际开发中,正确地设置和优化锁和索引对于构建高效、稳定的系统至关重要。下面是一些关于如何在实际开发中设置和优化锁和索引的建议: 锁…...
超详细彻底卸载Anaconda详细教程
一、在开始处打开Anaconda Prompt 二、打开后,输入conda install tqdm -f命令并按回车键 conda install tqdm -f三、之后页面会出现一个WANNING,这个我们不用在意,然后会出现一个y/n提示框,在这里我们输入y或者Y y四、输入cond…...
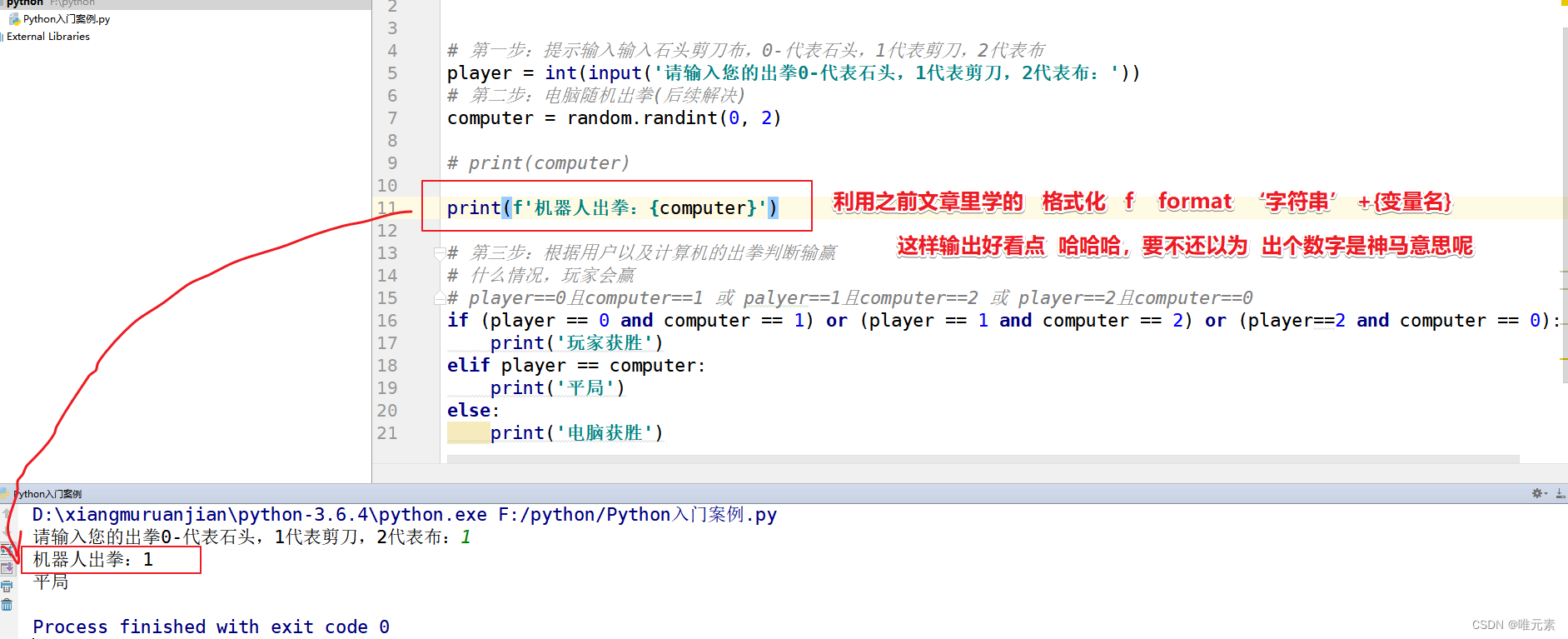
Python--随机出拳(random)--if判断--综合案例练习:石头剪刀布
注:涉及相关链接: Python:if判断--综合案例练习:石头剪刀布-CSDN博客 Python语言非常的强大,强大之处就在于其拥有很多模块(module),这些模块中拥有很多别人已经开发好的代码&…...

微信小程序里配置less
介绍 在微信小程序里,样式文件的后缀名都是wxss,这导致一个问题,就是页面样式过多的时候,要写很多的类名来包裹,加大了工作量,还很有可能会写错样式。这时可以配置一个less,会大大提高代码编辑…...
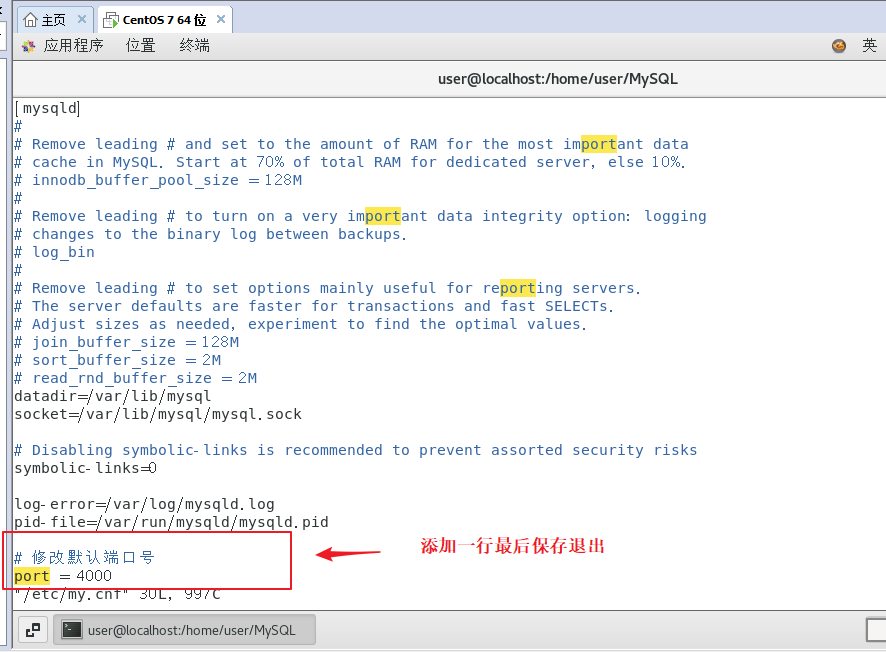
MySq修改配置文件
要修改 MySQL 的配置文件,您可以按照以下步骤进行操作: 1、打开 MySQL 的配置文件 在大多数 Linux 系统上,默认的配置文件路径是 /etc/my.cnf 或 /etc/mysql/my.cnf。您可以使用文本编辑器(如 vim、nano)以管理员权限打开该文件。 sudo vim /etc/my.cnf 2、进行修改 …...
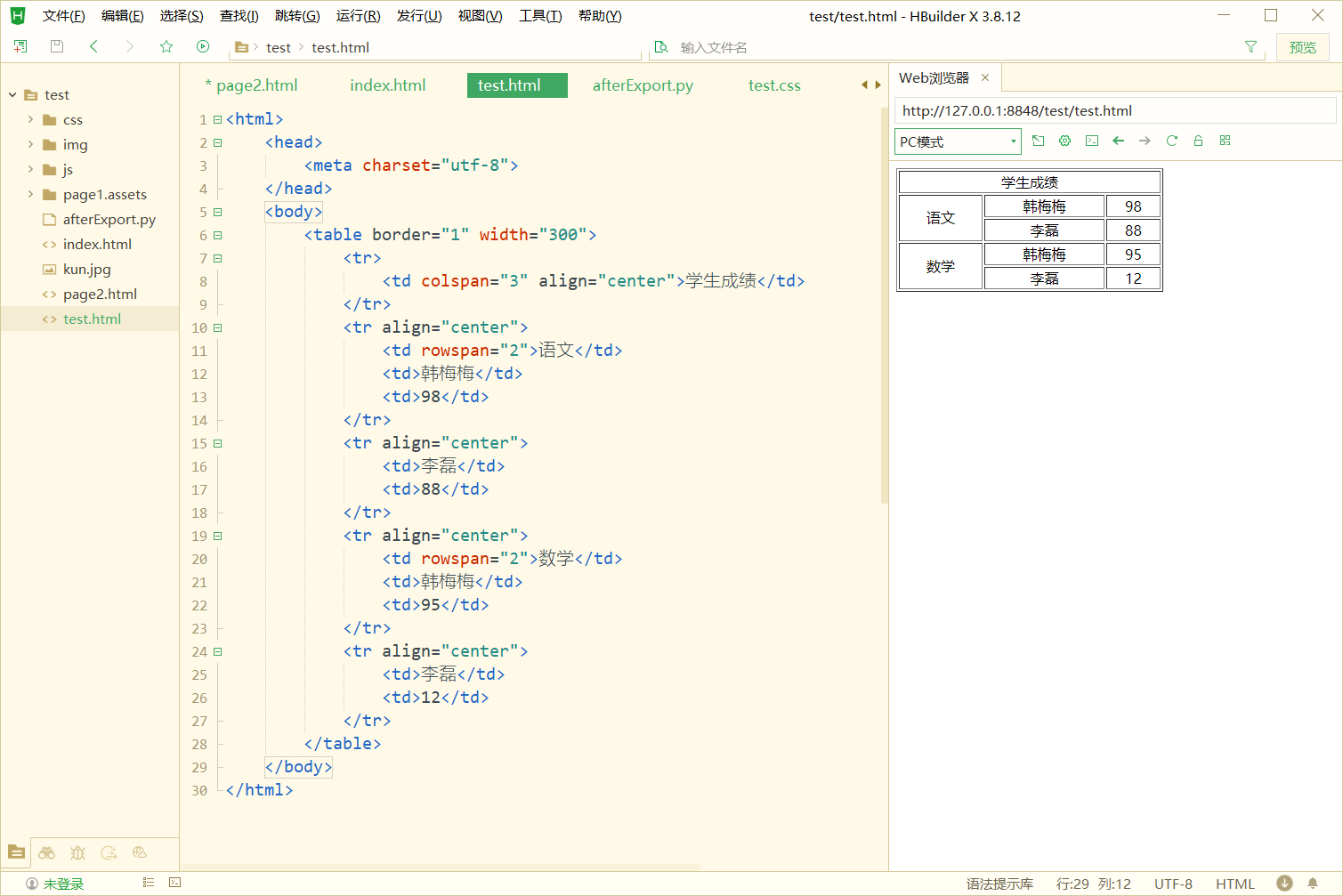
HTML 表格及练习
表格 概述 表格是一种二维结构,横行纵列。 由单元格组成。 表格是一种非常“强” 的结构: 每一行有相同的列数(单元格),每一列有相同的行数(单元格) 同一列的单元格,宽度&#…...
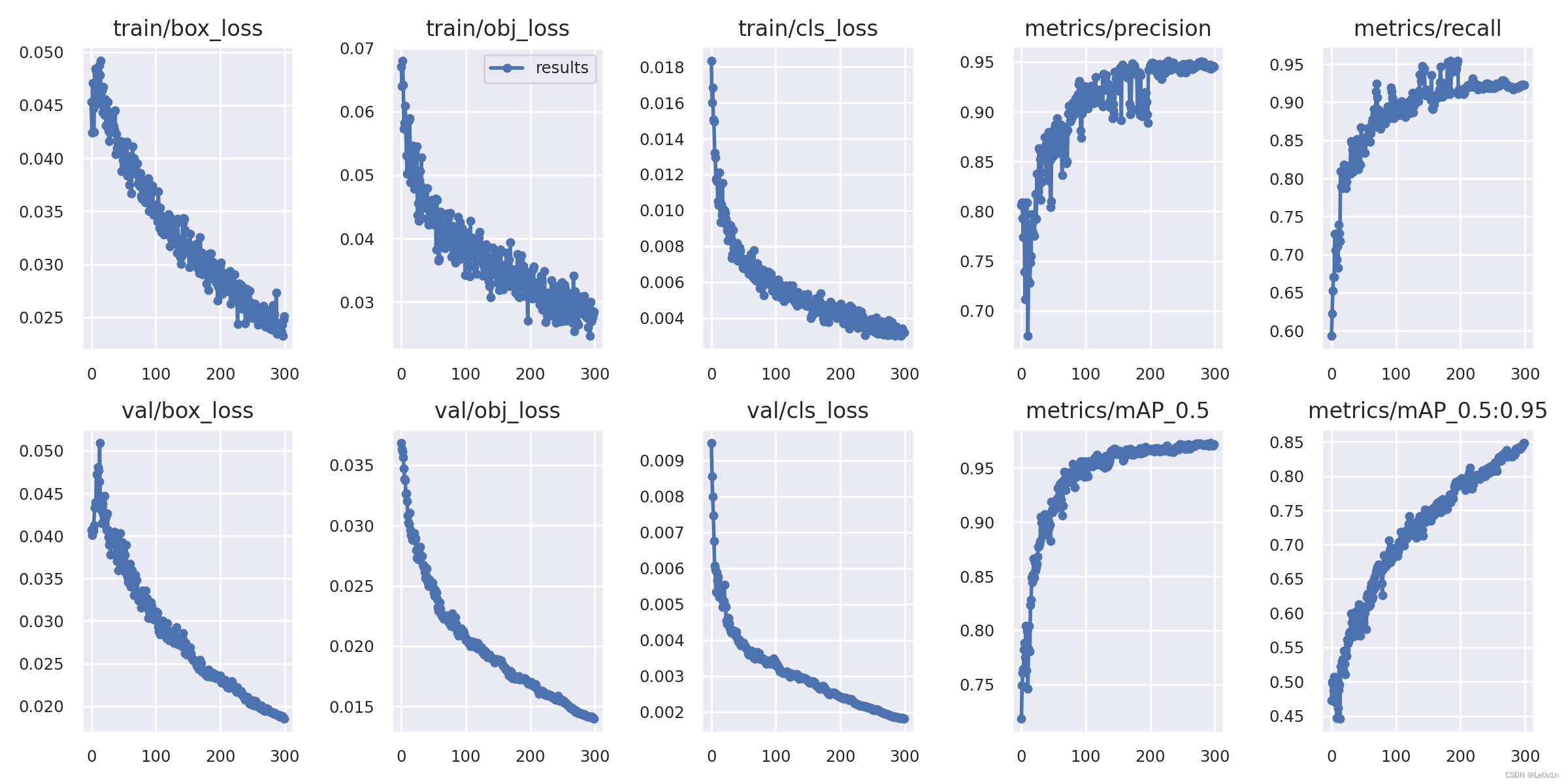
YOLOv5-训练自己的VOC格式数据集(VOC、自建数据集)
YOLOv5:训练自己的 VOC 格式数据集 1. 自定义数据集 1.1 环境安装 pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple注意: 安装 lxmlPillow 版本要低于 10.0.0,解释链接: module ‘PIL.Image’ has no attri…...
基于Java的考研信息查询系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding) 代码参考数据库参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者&am…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
