从零开始:GitFlow详细教程,轻松掌握分支策略
前序
GitFlow是一种用于管理Git仓库中软件开发工作流程的模型,它提供了一种结构化的方法来处理特性开发、版本发布和维护。下面是一个详细的GitFlow教程,帮助你了解GitFlow的基本概念和使用方法。
安装GitFlow
首先,确保你已经安装了Git。然后,可以通过以下方式安装GitFlow:
Windows
使用Git for Windows,它已经包括了GitFlow工具。
macOS
可以使用Homebrew来安装GitFlow:
brew install git-flow-avh
Linux
使用包管理器来安装GitFlow。例如,在Ubuntu上可以使用以下命令:
sudo apt-get install git-flow
初始化GitFlow
一旦安装了GitFlow,你可以在Git仓库中初始化它:
git flow init
此命令将引导你完成初始化过程,包括选择分支命名约定和分支的基本设置。
GitFlow分支概述
GitFlow定义了几种不同类型的分支,每个分支都有特定的用途:
-
主分支 (master): 主分支用于存储稳定的、生产就绪的代码。通常,只有发布后的代码才会合并到主分支。
-
开发分支 (develop): 开发分支是主要的开发分支,包含了当前正在进行的开发工作。所有新特性和bug修复都应该从develop分支创建。
-
特性分支 (feature): 特性分支用于开发新功能或添加新的功能模块。通常从develop分支创建,并在完成后合并回develop分支。
-
发布分支 (release): 发布分支用于准备发布版本。在发布前,你可以在这个分支上进行最后的测试和修复。发布分支通常从develop分支创建,并在发布后合并回develop和master分支。
-
热修复分支 (hotfix): 热修复分支用于紧急修复生产环境中的问题。它们从master分支创建,并在修复后合并回master和develop分支。
使用GitFlow
一旦你的Git仓库初始化了GitFlow,你可以按照以下步骤使用它:
创建特性分支
git flow feature start feature-name
这将创建一个新的特性分支,并将你切换到该分支,以便你可以在上面进行工作。
完成特性分支
在完成特性开发后,你可以将特性分支合并回develop分支:
git flow feature finish feature-name
创建发布分支
当你准备好发布新版本时,可以创建一个发布分支:
git flow release start release-version
完成发布分支
在发布分支上进行最后的测试和修复后,可以完成发布分支:
git flow release finish release-version
创建热修复分支
如果在生产环境中发现了问题,可以创建一个热修复分支:
git flow hotfix start hotfix-name
完成热修复分支
在修复问题后,可以完成热修复分支:
git flow hotfix finish hotfix-name
示例工作流程
以下是一个简单的GitFlow工作流程示例:
- 创建一个新的特性分支以开发一个新功能:
git flow feature start my-feature
- 在特性分支上进行开发,提交你的更改:
# 进行代码更改
git add .
git commit -m "Add new feature"
- 完成特性分支,将更改合并回develop分支:
git flow feature finish my-feature
- 创建一个新的发布分支以准备发布:
git flow release start 1.0.0
- 在发布分支上进行测试和修复,确保代码稳定:
# 进行测试和修复
git add .
git commit -m "Fix bugs"
- 完成发布分支,将更改合并回develop和master分支:
git flow release finish 1.0.0
- 如果在生产环境中发现了问题,可以创建一个热修复分支来解决问题:
git flow hotfix start hotfix-1.0.1
- 在热修复分支上进行修复,然后完成它:
# 进行修复
git add .
git commit -m "Fix critical bug"
git flow hotfix finish hotfix-1.0.1
这只是GitFlow的基本用法,它可以根据项目的需求进行自定义和扩展。GitFlow提供了一种结构化的方法来管理项目的开发和发布过程,有助于团队更好地协作和管理代码。
相关文章:

从零开始:GitFlow详细教程,轻松掌握分支策略
前序 GitFlow是一种用于管理Git仓库中软件开发工作流程的模型,它提供了一种结构化的方法来处理特性开发、版本发布和维护。下面是一个详细的GitFlow教程,帮助你了解GitFlow的基本概念和使用方法。 安装GitFlow 首先,确保你已经安装了Git。…...

深度学习硬件介绍
目录 1. 深度学习电脑选型1.1 深度学习常用框架1.2 深度学习硬件选择1.3 GPU 厂商介绍科普 你真的需要这么一块阵列卡 1. 深度学习电脑选型 1.1 深度学习常用框架 常见的深度学习框架:百度的飞桨框架、Google 的TensorFlow,伯克利亚学院的Caffe&#x…...
利用向导创建MFC
目录 1、项目的创建: 2、项目的管理 : 3、分析以及生成的项目代码 : (1)、查看CFrame中的消息映射宏 (2)、自动生成事件 (3)、在CFrame中添加对应的鼠标处理函数 …...
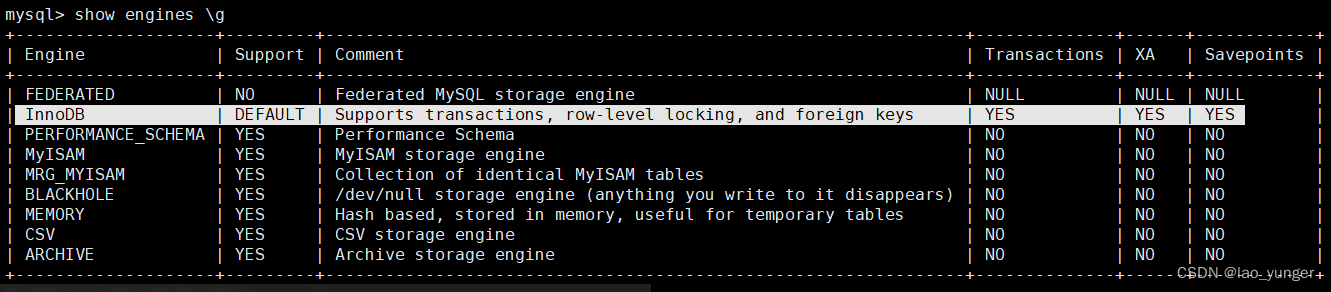
MySQL 8.0 OCP认证精讲视频、环境和题库之五 事务、缓存
redo log buffer: 缓存与事务有关的redo log ,用来对mysql进行crash恢复,不可禁用; 日志缓冲区是存储要写入磁盘上日志文件的数据的内存区域。日志缓冲区大小由innodb_Log_buffer_size变量定义。 默认大小为16MB。日志缓冲区的内容会定…...
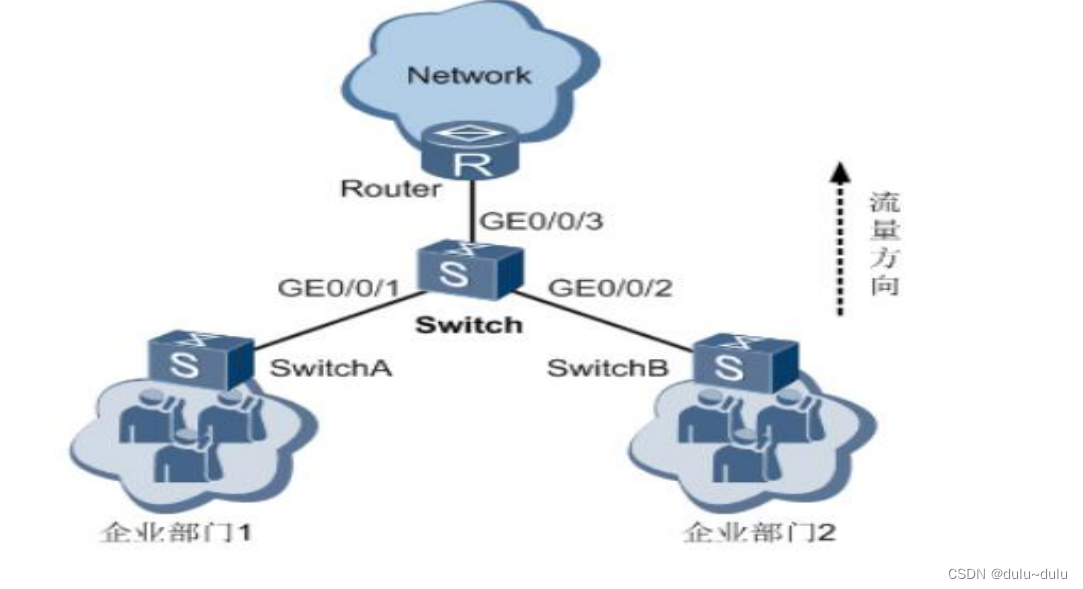
ACL配置
目录 1.使用基本ACL配置交换telnet访问的权限 2.使用高级ACL配置流分类实现限制互访某一台服务器 3.使用二层ACL配置流分类拒绝指定报文通过 4.通过流策略实现策略路由(重定向到不同的下一跳) 5.通过流策略实现不同网段间限制互访 6.通过流策略实现限速功能 7.通过流策略…...

微信小程序修改van-popup的背景颜色
效果图: van-popup背景颜色渐变 使用深度修改样式不生效,直接在 custom-style里面修改即可; <van-popup position"bottom"custom-style"height:25%;background:linear-gradient(95deg, #F8FCFF -0.03%, #EDF5FF 64.44…...
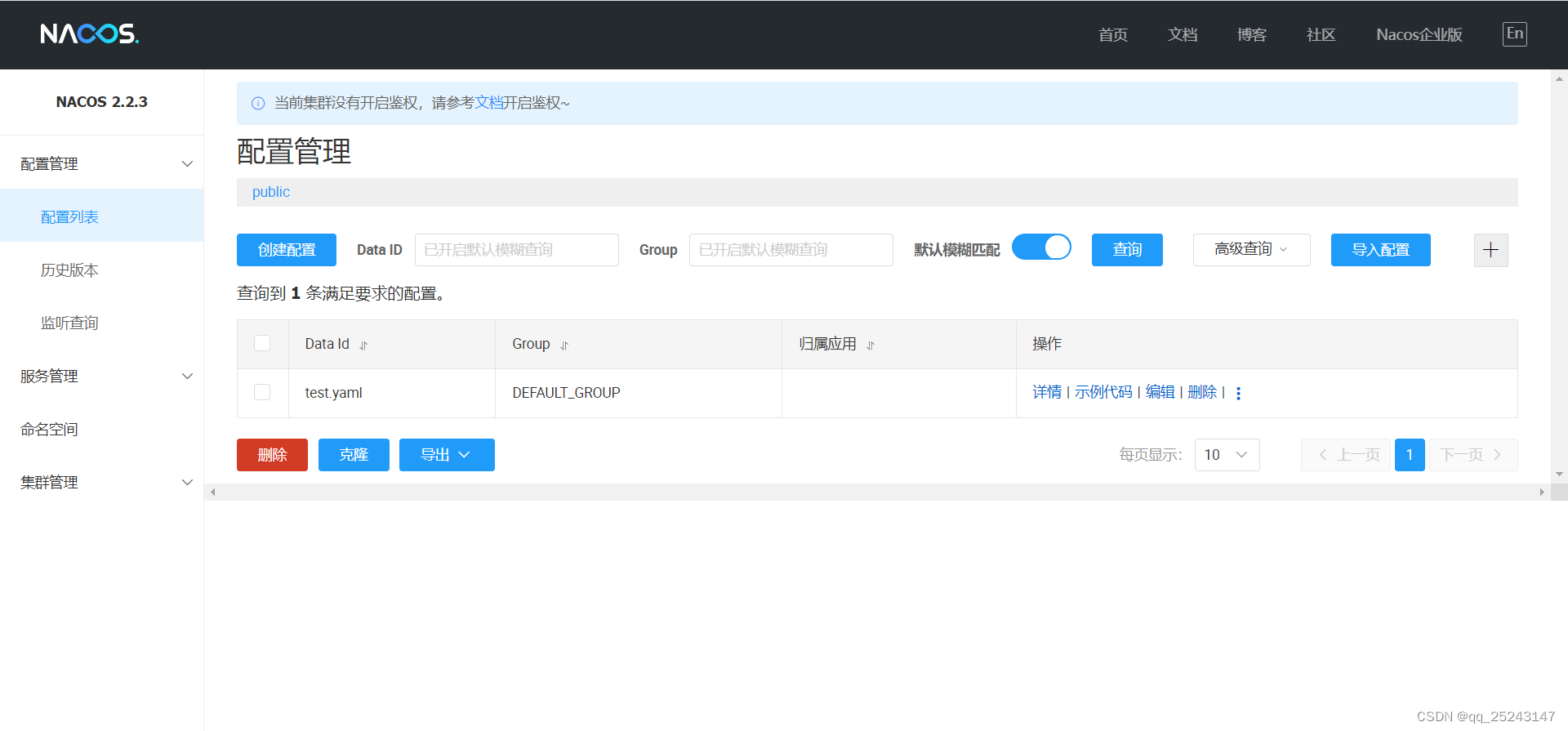
SpringCloud-Nacos
一、介绍 (1)作为服务注册中心和配置中心 (2)等价于:EurekaConfigBus (3)nacos集成了ribbon,支持负载均衡 二、安装 (1)官网 (2) …...
)
动态规划12(Leetcode221最大正方形)
代码: class Solution {public int maximalSquare(char[][] matrix) {int m matrix.length;int n matrix[0].length;int[][]area new int[m][n];area[0][0] matrix[0][0];int max 0;for(int i0;i<m;i){area[i][0] matrix[i][0]1? 1:0;max Math.max(area…...
【Git】bad signature 0x00000000 index file corrupt. fatal: index file corrupt
问题描述 电脑写代码时蓝屏。重启后 git commit 出错。 error: bad signature 0x00000000 fatal: index file corrupt原因分析 当电脑发生蓝屏或异常关机时,Git 的索引文件可能损坏。 解决方案 删除损坏的索引文件。 rm -Force .git/index回退到上一个可用的版…...

GO 语言的函数??
函数是什么? 学过编程的 xdm 对于函数自然不会陌生,那么函数是什么呢? 函数是一段可以重用的代码块,可以被多次调用,我们可以通过使用函数,提高咱们代码代码的模块化,提高程序的可读性和可维护…...
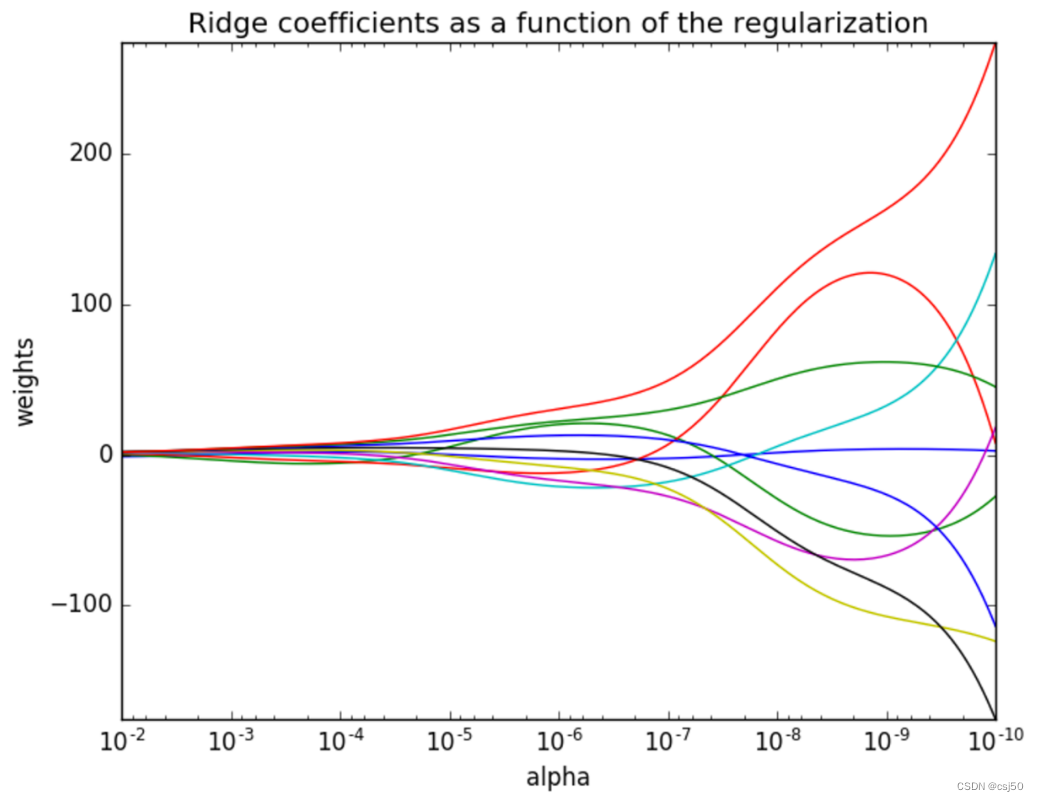
机器学习基础之《回归与聚类算法(3)—线性回归优化:岭回归》
一、什么是岭回归 其实岭回归就是带L2正则化的线性回归 岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上L2正则化的限制,从而达到解决过拟合的效果 二、API 1、sklearn.linear_model.Ridge(alpha1.0, fit_interceptTrue…...
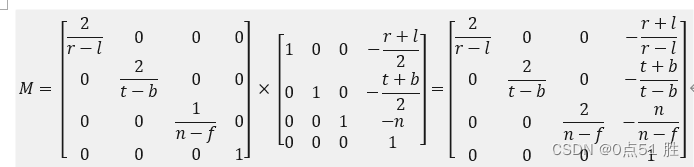
DirectX3D 正交投影学习记录
所谓正交投影变换,就是已知盒状可视空间内任意点坐标(x,y,z),求解垂直投影到xy平面的对应点坐标。 按照这个定义,xyz坐标系本身就是正交坐标系,盒状可视空间内任意点的坐标(x,y,z)投影到(x,y)平面,只要简单地丢弃z坐标…...
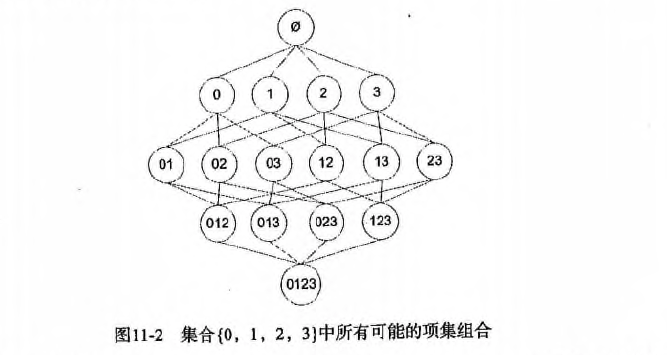
数据挖掘十大算法--Apriori算法
一、Apriori 算法概述 Apriori 算法是一种用于关联规则挖掘的经典算法。它用于在大规模数据集中发现频繁项集,进而生成关联规则。关联规则揭示了数据集中项之间的关联关系,常被用于市场篮分析、推荐系统等应用。 以下是 Apriori 算法的基本概述&#x…...

[蓝桥杯 2022 省 B] 统计子矩阵
题目描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵 (最小 11, 最大 NM) 满足子矩阵中所有数的和不超过给定的整数 K。 输入格式 第一行包含三个整数 N, M和 K。 之后 N 行每行包含 M 个整数, 代表矩阵 A。 输出格式 一个整数代表答案。 输入输出样例 输入 #1 3…...

解决在部署springboot项目的docker中执行备份与之相连接的mysql容器命令
文章目录 问题描述解决思路问题解决容器构建mysql客户端安装容器与主机的交互docker中执行 mysqldump 命令解决mysql8密码验证问题解决密码插件警告 问题描述 由于,使用1panel可视化的面板来部署springboot项目,可以很方便地安装和使用mysql,…...

正文Delphi XE Android下让TMemo不自动弹出键盘
用TMemo来显示一段说明文字,可一点Memo,就弹出键盘,找了半天控制键盘的属性,没找到。最后将readOnly设置为True搞定。 如果需要一个form都不显示keyboard,那么可以利用全局变量 VKAutoShowMode来控制,这个全局变量可以有下面三个值…...

[1Panel]开源,现代化,新一代的 Linux 服务器运维管理面板
测评介绍 本期测评试用一下1Panel这款面板。1Panel是国内飞致云旗下开源产品。整个界面简洁清爽,后端使用GO开发,前端使用VUE的Element-Plus作为UI框架,整个面板的管理都是基于docker的,想法很先进。官方还提供了视频的使用教程&…...
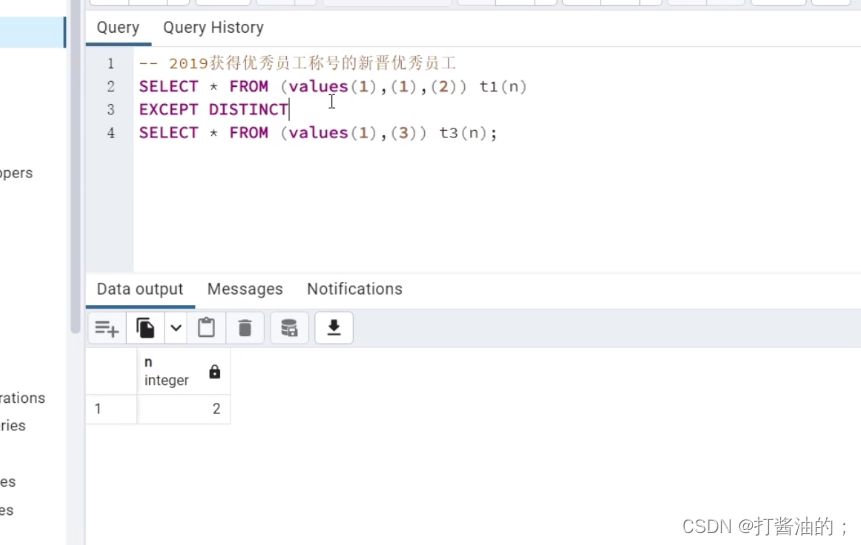
PG集合查询
1.运算符 1.1 union并集 连接上下语句 union distinct连接并且去重 all不去重 1.2 intersect交集 上下交集 distinct连接并且去重 all不去重 1.3 except除外 上面除了下面 distinc去重 all不去重...
目标检测应用场景和发展趋势
参考: 目标检测的未来是什么? - 知乎 (zhihu.com)https://www.zhihu.com/question/394900756/answer/32489649815大应用场景 1 行人检测: 遮挡问题:行人之间的互动和遮挡是非常常见的,这给行人检测带来了挑战。非刚性…...
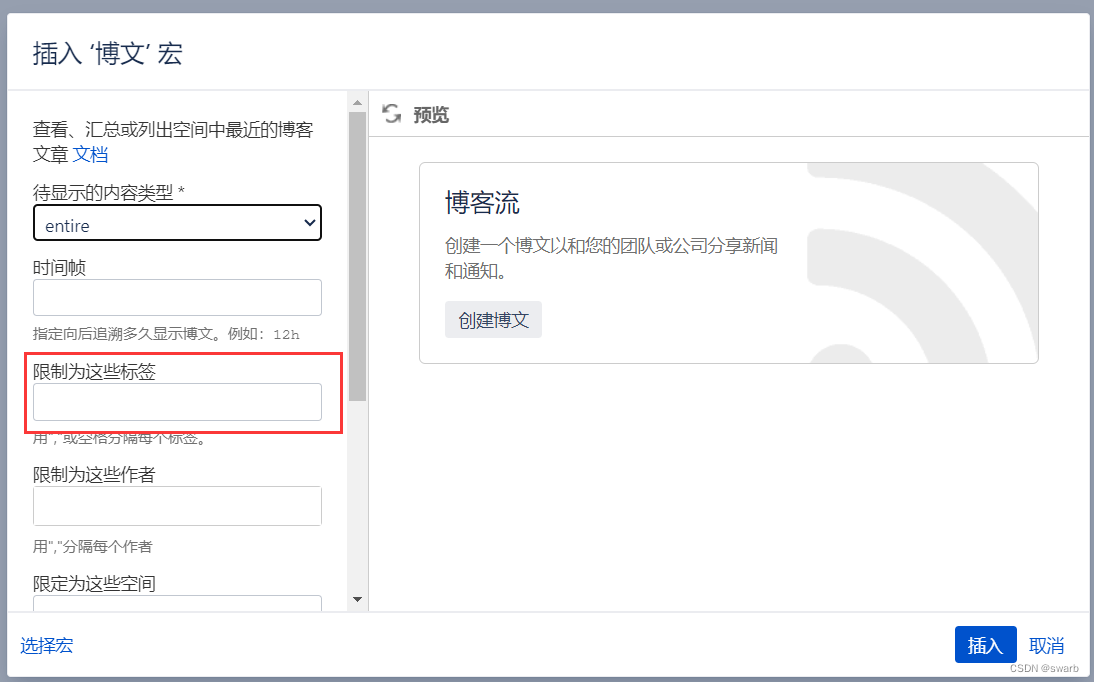
Confluence 自定义博文列表
1. 概述 Confluence 自有博文列表无法实现列表自定义功能,实现该需求可采用页面中引用博文宏标签控制的方式 2. 实现方式 功能入口: Confluence →指定空间→创建页面 功能说明: (1)页面引用博文宏 (…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
