LeetCode 2906. 构造乘积矩阵【前后缀分解,数组】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个下标从 0 开始、大小为 n * m 的二维整数矩阵 grid ,定义一个下标从 0 开始、大小为 n * m 的的二维矩阵 p。如果满足以下条件,则称 p 为 grid 的 乘积矩阵 :
- 对于每个元素
p[i][j],它的值等于除了grid[i][j]外所有元素的乘积。乘积对12345取余数。
返回 grid 的乘积矩阵。
示例 1:
输入:grid = [[1,2],[3,4]]
输出:[[24,12],[8,6]]
解释:p[0][0] = grid[0][1] * grid[1][0] * grid[1][1] = 2 * 3 * 4 = 24
p[0][1] = grid[0][0] * grid[1][0] * grid[1][1] = 1 * 3 * 4 = 12
p[1][0] = grid[0][0] * grid[0][1] * grid[1][1] = 1 * 2 * 4 = 8
p[1][1] = grid[0][0] * grid[0][1] * grid[1][0] = 1 * 2 * 3 = 6
所以答案是 [[24,12],[8,6]] 。
示例 2:
输入:grid = [[12345],[2],[1]]
输出:[[2],[0],[0]]
解释:p[0][0] = grid[0][1] * grid[0][2] = 2 * 1 = 2
p[0][1] = grid[0][0] * grid[0][2] = 12345 * 1 = 12345. 12345 % 12345 = 0 ,所以 p[0][1] = 0
p[0][2] = grid[0][0] * grid[0][1] = 12345 * 2 = 24690. 24690 % 12345 = 0 ,所以 p[0][2] = 0
所以答案是 [[2],[0],[0]] 。
提示:
1 <= n == grid.length <= 10^51 <= m == grid[i].length <= 10^52 <= n * m <= 10^51 <= grid[i][j] <= 10^9
前后缀分解(右边的数字为难度分)
- 238. 除自身以外数组的乘积 和本题几乎一样
- 剑指Offer66. 构建乘积数组 和本题几乎一样
- 2256. 最小平均差 1395
- 2483. 商店的最少代价 1495
- 2420. 找到所有好下标 1695
- 2167. 移除所有载有违禁货物车厢所需的最少时间 2219
- 2484. 统计回文子序列数目 2223
- 2565. 最少得分子序列 2432
- 2552. 统计上升四元组 2433
- 42. 接雨水
解法 前后缀分解
核心思想:把矩阵拉成一维的,我们需要算出每个数左边所有数的乘积,以及右边所有数的乘积,这都可以用递推得到。
先算出从 g r i d [ i ] [ j ] grid[i][j] grid[i][j] 的下一个元素开始,到最后一个元素 g r i d [ n − 1 ] [ m − 1 ] grid[n−1][m−1] grid[n−1][m−1] 的乘积,记作 s u f [ i ] [ j ] suf[i][j] suf[i][j] 。这可以从最后一行最后一列开始,倒着遍历得到。
然后算出从第一个元素 g r i d [ 0 ] [ 0 ] grid[0][0] grid[0][0] 开始,到 g r i d [ i ] [ j ] grid[i][j] grid[i][j] 的上一个元素的乘积,记作 p r e [ i ] [ j ] pre[i][j] pre[i][j] 。这可以从第一行第一列开始,正着遍历得到。
那么: p [ i ] [ j ] = p r e [ i ] [ j ] ⋅ s u f [ i ] [ j ] p[i][j]=pre[i][j]⋅suf[i][j] p[i][j]=pre[i][j]⋅suf[i][j]
代码实现时,可以先初始化 p [ i ] [ j ] = s u f [ i ] [ j ] p[i][j]=suf[i][j] p[i][j]=suf[i][j] ,然后把 p r e [ i ] [ j ] pre[i][j] pre[i][j] 乘到 p [ i ] [ j ] p[i][j] p[i][j] 中,就得到了答案。这样 p r e pre pre 和 s u f suf suf 就可以压缩成一个变量。
class Solution {
public:vector<vector<int>> constructProductMatrix(vector<vector<int>>& grid) {const int MOD = 12345;int n = grid.size(), m = grid[0].size();vector<vector<int>> p(n, vector<int>(m));long long suf = 1; // 后缀乘积for (int i = n - 1; i >= 0; --i) {for (int j = m - 1; j >= 0; --j) {p[i][j] = suf; // p[i][j]先初始化为后缀乘积suf = suf * grid[i][j] % MOD;}}long long pre = 1; // 前缀乘积for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {p[i][j] = p[i][j] * pre % MOD; // 然后再乘上前缀乘积pre = pre * grid[i][j] % MOD;}}return p;}
};
复杂度分析:
- 时间复杂度: O ( n m ) \mathcal{O}(nm) O(nm) ,其中 n n n 和 m m m 分别为 grid \textit{grid} grid 的行数和列数。
- 空间复杂度: O ( 1 ) \mathcal{O}(1) O(1) 。返回值不计入。
相关文章:

LeetCode 2906. 构造乘积矩阵【前后缀分解,数组】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

vue3+koa+axios实现前后端通信
vue3koaaxios实现前后端通信 写了一个小demo来实现前后端通信,涉及跨域问题,非常简单可以给大家平时开发的时候参考 服务端: 目录结构如下: router index.js // router的入口文件 // 引入路由 const Router require("koa-router&quo…...
Required MultipartFile parameter ‘file‘ is not present
出现这个原因我们首先想到的是加一个RequestParam("file"),但是还有可能的原因是因为我们的名字有错误 <span class"input-group-addon must">模板上传 </span> <input id"uploadFileUpdate" name"importFileU…...

vue3后台管理系统之layout组件的搭建
1.1静态布局 <template><div class"layout_container"><!-- 左侧导航 --><div class"layout_slider"></div><!-- 顶部导航 --><div class"layout_tabbar"></div><!-- 内容展示区 --><…...

Minio 文件上传(后端处理同文件判断,同一文件秒传)
记录minio 文件上传 MinIO提供多个语言版本SDK的支持,下边找到java版本的文档: 地址:https://docs.min.io/docs/java-client-quickstart-guide.html maven依赖如下: XML <dependency><groupId>io.minio</groupId…...
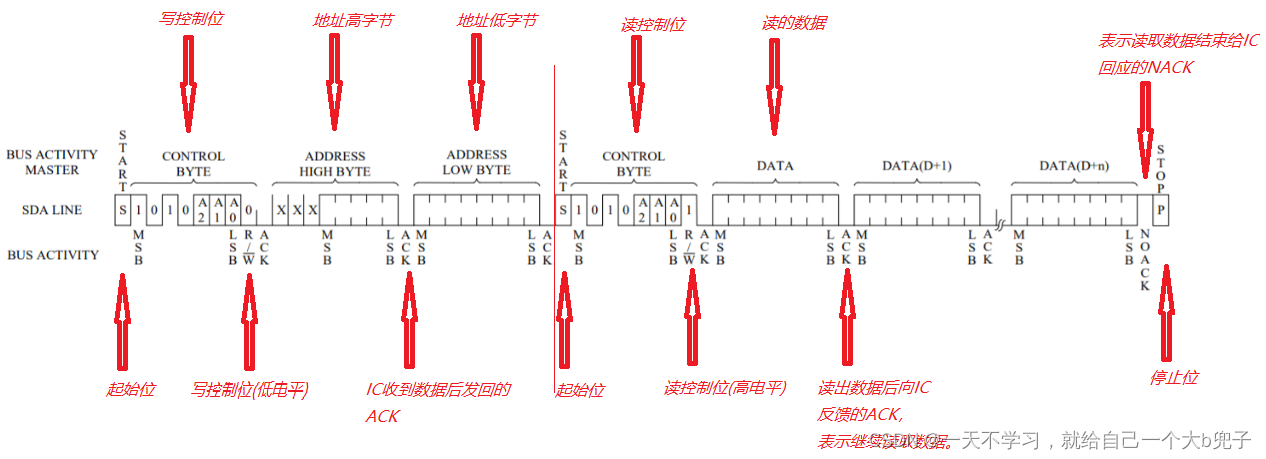
模拟IIC通讯协议(stm32)(硬件iic后面在补)
一、IIC基础知识总结。 1、IIC通讯需要两条线就可以,SCL、SDA。 2、IIC的数据传输的速率,不同的ic是不同的,根据电平维持的延时函数的时间来确定IIC数据传输的速率. 3、IIC的延时函数可以使用延时函数,延时函数一般使用系统滴答时…...

使用注解读取properties配置文件
文章目录 1、背景2、注解方式2.1 PropertySource 、 ConfigurationProperties2.2 读取properties中全部字段值ConfigurationProperties2.3 读取properties中部分字段值:value("${自定义key}") 1、背景 服务中使用到了redis,需要配置redis连接…...

Python---练习:求世界杯小组赛的总成绩(涉及:布尔类型转换为整型)
案例 世界杯案例 需求: 世界杯案例,世界杯小组赛的比赛规则是我们的球队与其他三支球队进行比赛,然后根据总成绩(积分)确定出线资格。小组赛球队实力已知(提示用户输入各球队实力),我们通过一个数字表示。如果我们赢…...

vue3学习源码笔记(小白入门系列)------KeepAlive 原理
目录 说明组件是如何被缓存的,什么时候被激活对于KeepAlive 中组件 如何完成激活的对于KeepAlive 中组件 如何完成休眠的 总结 说明 Vue 内置了 KeepAlive 组件,实现缓存多个组件实例切换时,完成对卸载组件实例的缓存,从而使得组…...
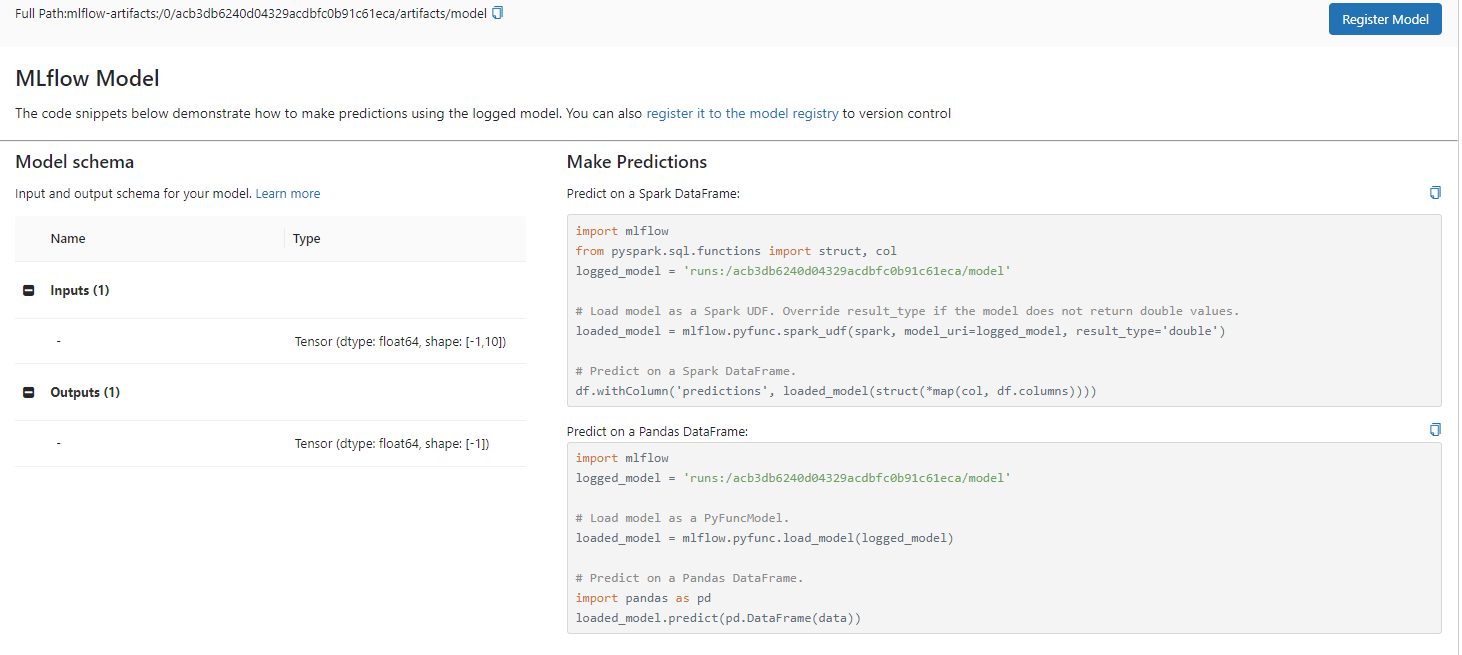
边写代码边学习之mlflow
1. 简介 MLflow 是一个多功能、可扩展的开源平台,用于管理整个机器学习生命周期的工作流程和工件。 它与许多流行的 ML 库内置集成,但可以与任何库、算法或部署工具一起使用。 它被设计为可扩展的,因此您可以编写插件来支持新的工作流程、库和…...

基于吉萨金字塔建造优化的BP神经网络(分类应用) - 附代码
基于吉萨金字塔建造优化的BP神经网络(分类应用) - 附代码 文章目录 基于吉萨金字塔建造优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.吉萨金字塔建造优化BP神经网络3.1 BP神经网络参数设置3.2 吉萨金字…...

axios的post请求所有传参方式
Axios支持多种方式来传递参数给POST请求。以下是一些常见的方式: 作为请求体: 你可以将参数作为请求体的一部分,通常用于发送表单数据或JSON数据。例如: const data { key1: value1, key2: value2 }; axios.post(/api/endpoint, …...
【c++】向webrtc学比较2: IsNewerSequenceNumber 用于NackTracker及测试
LatestSequenceNumber inline uint16_t LatestSequenceNumber(uint16_t sequence_number1,uint16_t sequence_number2) {return IsNewerSequenceNumber(sequence_number1, sequence_number2)? sequence_number1: sequen...

PRCV 2023:语言模型与视觉生态如何协同?合合信息瞄准“多模态”技术
近期,2023年中国模式识别与计算机视觉大会(PRCV)在厦门成功举行。大会由中国计算机学会(CCF)、中国自动化学会(CAA)、中国图象图形学学会(CSIG)和中国人工智能学会&#…...
)
深度学习硬件配置推荐(kaggle学习)
目录 1. 基础推荐2. GPU显存与内存是一个1:4的配比?3. deep learning 入门和kaggle比赛4. 有些 Kaggle 比赛数据集很大,可能需要更多的 GPU 显存,请推荐显存4. GDDR6和HBM25. HDD 或 SATA SSD 1. 基础推荐 假设您作为一个深度学习入门学者的…...
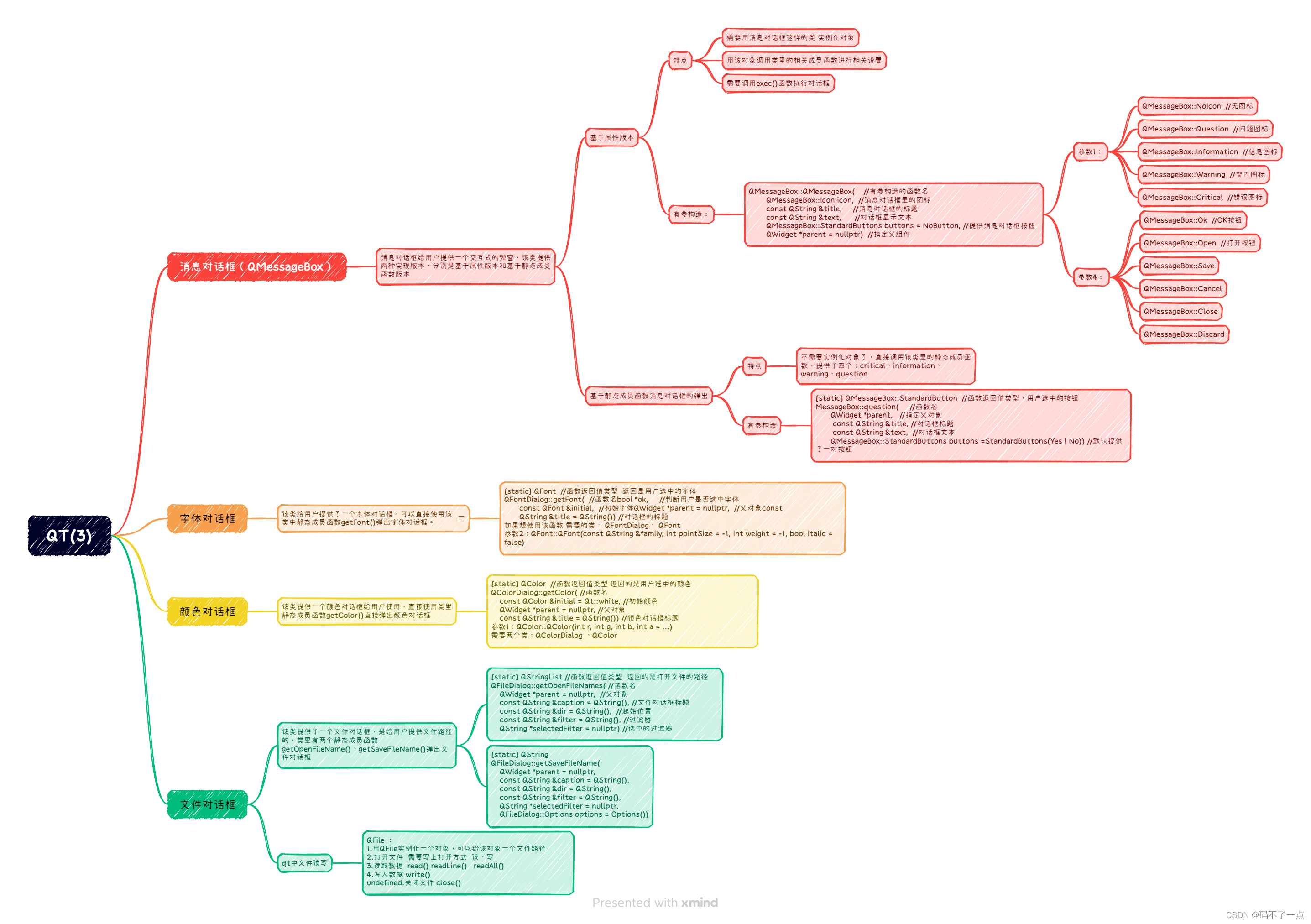
1019hw
登录窗口头文件 #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QMainWindow> #include <QToolBar> #include <QMenuBar> #include <QPushButton> #include <QStatusBar> #include <QLabel> #include <QDockWidget>//浮动窗口…...

两分钟搞懂UiAutomator自动化测试框架
1. UiAutomator简介 UiAutomator是谷歌在Android4.1版本发布时推出的一款用Java编写的UI测试框架,基于Accessibility服务。其最大的特点就是可以跨进程操作,可以使用UiAutomator框架提供的一些方便的API来对安卓应用进行一系列的自动化测试操作…...
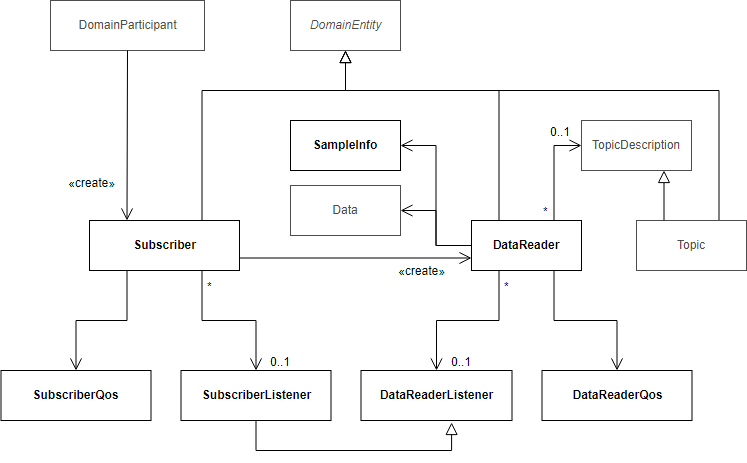
Fast DDS之Subscriber
目录 SubscriberSubscriberQosSubscriberListener创建Subscriber DataReaderSampleInfo读取数据 Subscriber扮演容器的角色,里面可以有很多DataReaders,它们使用Subscriber的同一份SubscriberQos配置。Subscriber可以承载不同Topic和数据类型的DataReade…...

测试PySpark
文章最前: 我是Octopus,这个名字来源于我的中文名--章鱼;我热爱编程、热爱算法、热爱开源。所有源码在我的个人github ;这博客是记录我学习的点点滴滴,如果您对 Python、Java、AI、算法有兴趣,可以关注我的…...

C语言- 原子操作
基本概念 在C语言(尤其是C11标准之后)中,原子操作提供了一种机制,使得程序员可以在并发环境中,不使用互斥或其他同步原语,而直接对数据进行操作,同时确保数据的完整性和一致性。 原子变量和原子操作的核心思想是:无论什么时候,只有一个线程能够看到变量的修改操作。…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
