11. 机器学习 - 评价指标2
文章目录
- 混淆矩阵
- F-score
- AUC-ROC

更多内容: 茶桁的AI秘籍
Hi, 你好。我是茶桁。
上一节课,咱们讲到了评测指标,并且在文章的最后提到了一个矩阵,我们就从这里开始。
混淆矩阵
在我们实际的工作中,会有一个矩阵,这个矩阵是分析结果常用的。
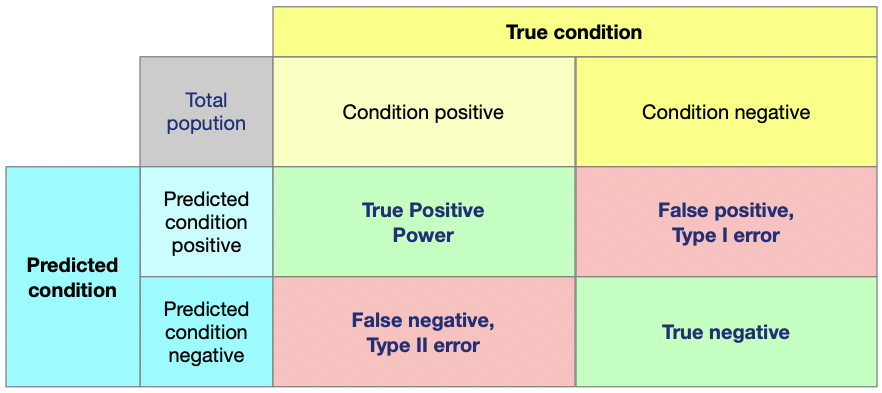
我们来看看具体是什么意思。
所谓的True condition, 指的是真实值, Predicted condition,指的是预测值。
其中行表示,Predicted condition positive表示预测值是1,Predicted condition negative表示预测值是0。
列表示则为:Condition positive表示真实值是1, Condition negative表示真实值是0。
这样行列交叉就组成了这样一个矩阵。这个矩阵叫做混淆矩阵, 英文名字叫做Confusion Matrix.
这个混淆矩阵是什么意思呢?
True Positive 意思就是预测值是1, 预测对了,True negative意思是预测值是0, 预测对了。那相对的, False positive意思就是预测值是1, 预测错了, False negative意思就是预测值是0, 预测错了。
混淆矩阵在常见的机器学习里边是一个很重要的分析工具:
from sklearn.metrics import confusion_matrix
confusion_matrix(true_labels, predicated_labels)—
array([[59, 6],[ 6, 29]])
我们可以直接看看这个方法的源码里有相关说明:
??confusion_matrix---
def confusion_matrix(...the count of true negatives is :math:`C_{0,0}`, false negatives is :math:`C_{1,0}`, true positives is :math:`C_{1,1}` false positives is :math:`C_{0,1}`....
tp实际上是1预测值是1,tn实际是0预测是0, fp实际是0预测是1 fn实际是1预测是0。
這個時候我們再回頭來看上节课结尾处的那个公式:
P r e c i s i o n = t p t p + f p R e c a l l = t p t p + f n \begin{align*} Precision & = \frac{tp}{ tp + fp} \\ Recall & = \frac{tp}{tp + fn} \end{align*} PrecisionRecall=tp+fptp=tp+fntp
很多人看到这个就有点晕, 其实很简单. 切换成我们刚才查看源码时查询到的就就成了这样:
P r e c i s i o n = C ( 0 , 0 ) C ( 0 , 0 ) + C ( 1 , 0 ) R e c a l l = C ( 0 , 0 ) C ( 0 , 0 ) + C ( 0 , 1 ) \begin{align*} Precision & = \frac{C(0, 0)}{ C(0, 0) + C(1, 0)} \\ Recall & = \frac{C(0, 0)}{C(0, 0)+ C(0, 1)} \end{align*} PrecisionRecall=C(0,0)+C(1,0)C(0,0)=C(0,0)+C(0,1)C(0,0)
tp是实际上是positive, 预测也是positive. fp就是实际上并不是positive,但是预测的值是positive. 那么tp+fp就是所有预测为positive的值. 所以precision就是预测对的positive比上所有预测的positive.
fn指的是实际上是positive, 但是预测值并不是positive的值. 所以tp+fn就是所有实际的positive值, recall就是预测对的positive比上所有实际的positive值.
我们这样对比着矩阵和公式来理解Precision和Recall是不是就清晰了很多? 这就是position和recall根据混淆矩阵的一种定义方式.
刚刚讲了baseline, baseline是在做评估的时候要知道结果一定要比什么好才行.如果是个二分类问题, 基本上是一半一半, 准确度是50%, 那基本上就没用.
Precision和recall这两个是针对于分类问题进行评价, 那我们怎么解决回归问题的评价呢?
回归问题,它也有一个accuracy如下:
a c c ( y , y ^ ) = ∑ i ∈ N ∣ y i − y ^ i ∣ a c c ( y , y ^ ) = ∑ i ∈ N ∣ y i − y ^ i ∣ 2 a c c ( y , y ^ ) = ∑ i ∈ N ∣ y i − y i ^ ∣ ∣ y i ∣ acc(y, \hat y) = \sum_{i \in N}|y_i - \hat y_i| \\ acc(y, \hat y) = \sum_{i \in N}|y_i - \hat y_i|^2 \\ acc(y, \hat y) = \sum_{i \in N} \frac{|y_i - \hat{y_i}|}{|y_i|} acc(y,y^)=i∈N∑∣yi−y^i∣acc(y,y^)=i∈N∑∣yi−y^i∣2acc(y,y^)=i∈N∑∣yi∣∣yi−yi^∣
除此之外, regression问题里面有一个比较重要的评价方式叫做R2-scoree:
R 2 ( y , y ^ ) = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 R^2(y, \hat y) = 1 - \frac{\sum_{i=1}^n(y_i - \hat y_i)^2}{\sum_{i=1}^n(y_i - \bar y)^2} R2(y,y^)=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
- 第一种情况: 如果所有的y_i和yhat_i的值都相等, 那么R2(y, yhat) = 1
- 第二种情况: 如果所有的yhat_i是y_i的平均值, 那么R2(y, yhat) = 0
- 第三种情况: 如果R2的值比0还小, 就意味着它还不如我们做统计求平均值,瞎猜的结果. 也就是连baseline都没达到.
R2-scoree之所以常常会被用于进行回归问题的评测, 主要的原因就是它防止了机器作弊.
比方说我们现在有一组数据, 这组数据实际都是0.99, 0.97, 0.98…, 这些数字都很小, 而且都很密集. 那么给机器使用的时候随便做一个平均值, 感觉到准确度还挺高, 那就被骗了.
F-score
在precision和recall之外, 还有一个比较重要的内容, 叫做F-score.
首先我们要知道, precision和recall这两个值在实际工作中往往是相互冲突的. 为了做个均衡, 就有了F-score.
F − s c o r e = ( 1 + β 2 ) ∗ p r e c i s i o n × r e c a l l β 2 ∗ p r e c i s i o n + r e c a l l \begin{align*} F-score & = \frac{(1+\beta^2) * precision \times recall}{\beta^2 * precision + recall} \end{align*} F−score=β2∗precision+recall(1+β2)∗precision×recall
β \beta β是自行定义的参数,由这个式子可见F-score能同时考虑precision和recall这两种数值。分子为precision和recall相乘,根据式子,只要precision或recall趋近于0,F-score就会趋近于0,代表着这个算法的精确度非常低。一个好的算法,最好能够平衡recall和precision,且尽量让两种指标都很高。所以有一套判断方式可以同时考虑recall和precision。当 β → 0 \beta \to 0 β→0, F-score就会退化为precision, 反之, 当 β → ∞ \beta \to \infty β→∞, F-socre就会退化为recall.
我们一般说起来, F-score没有特别定义的话, 就是说 β \beta β为1, 一般我们写成F1-score.
F 1 − s c o r e = 2 × p r e c i s i o n × r e c a l l p r e c i s i o n + r e c a l l \begin{align*} F1-score & = 2 \times \frac{precision \times recall}{precision + recall} \end{align*} F1−score=2×precision+recallprecision×recall
F1-score是仅当precision和recall都为1的时候,其值才等于1. 而如果这两个值中任意一个不为1时,其值都不能等于1. 也就是说,当2*1/2 = 1时, F1-score=100%, 代表该算法有着最佳的精确度.
AUC-ROC
除了F-score之外,还有比较重要的一个概念: AUC-ROC. 这个也是为了解决样本不均衡提出来的一个解决方案.
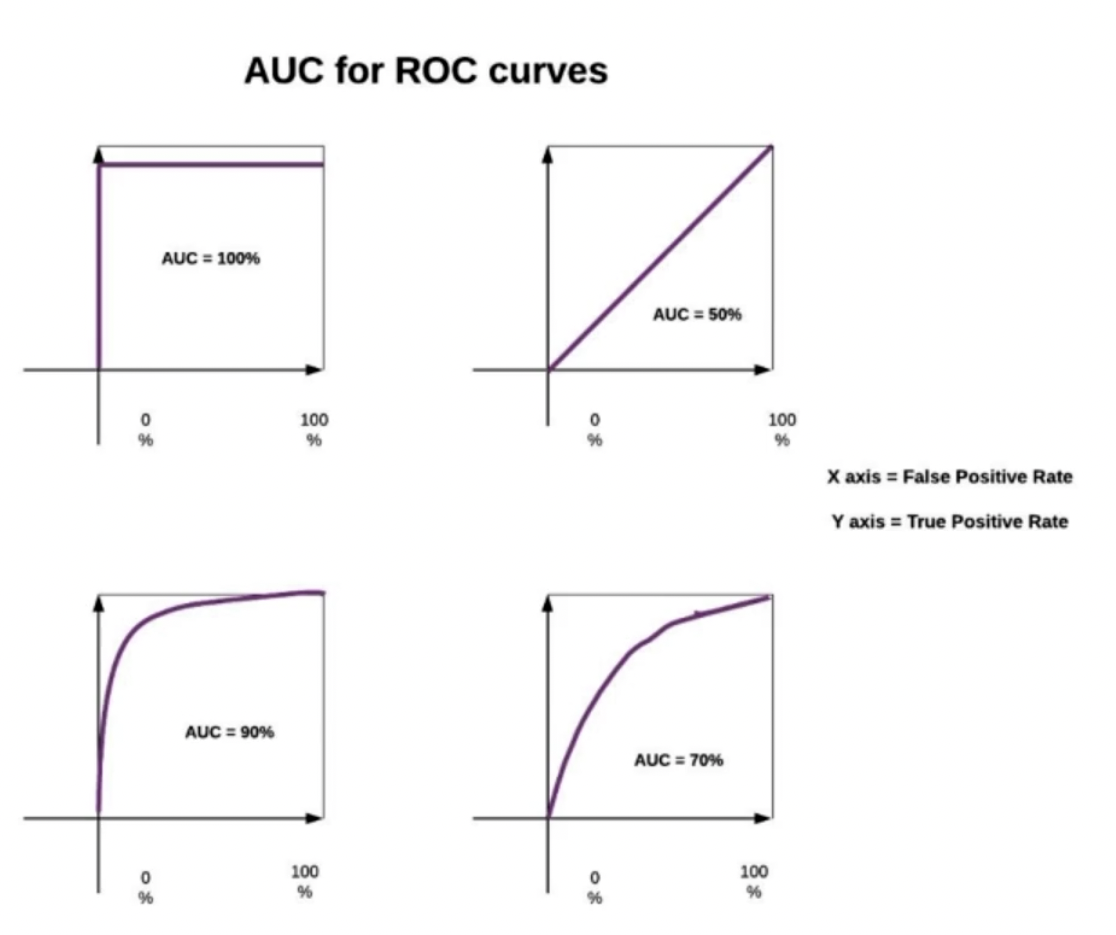
首先我们要先了解ROC曲线(receiveroperating characteristic), ROC曲线上的每一个点反映着对同一信号刺激的感受. AOC(Area under Curve), 是ROC曲线下的面积, 取值是在0.1 ~ 1 之间.
我们直接来看看,它在实际场景下是怎么用的.
还记得咱们在之前设定的阈值decision_boundary = 0.5, 我们就拿这个阈值来看. threshold:0.5. 在我们二分类问题中, 当预测值大于0.5的时候,也就等于1了. 也就是说,只要超过0.5, 我们就判定为positive值.
好,现在还是的请我们劳烦了无数次的警察a同志来帮帮我们. 当警察a去抓罪犯的时候,盘但一个人是不是犯了罪, 他的决策很重要. 在事实清晰之前,警察a的决策只有超过0.5的时候,才能判定这个人是positive,也就是罪犯. 这个时候呢,我们假设precision是0.7.
现在又需要警察b出场了, 这个警察b的threshold为0.1的时候, 其precision就为0.7. 也就是说,他预计出的值,只要大于0.1, 就判定为positive, 这种情况下, 警察b判定的precision为0.7.
别急,这次需要的演员有点多,所以,警察c登场了. 那么警察c的threshold为0.9. 也就是说,警察c比较谨慎, 只有非常确定的时候, 才能判定positive. 警察c的情况,判定的precision也是0.7.
好,现在我们来用脑子思考下, 这三个警察哪个警察能力最强?
必须是警察b最厉害.
就如我们上面的那四个坐标轴, X轴代表threshold, Y轴表实positive, 当threshold轴上的取值还很小的时候, positive已经很大了.那明显紫色线条和threshold轴圈住的区域面积越大, 这个面积就是越大越好.
这就是AUC for ROC curves, 这个主要就是为了解决那些样本及其不均衡的问题. 因为样本非常不均衡的时候, position和recall你有可能都会很低, 这个时候就不好对比. AUC曲线对于这种情况就比较好用一些.
其实在真实情况下, 绝大多数问题都不是很均衡的问题. 比方说预测病, 找消费者, 找高潜力用户. 换句话说, 如果高潜用户多就不用找了.
我们在研究ROC曲线实际应用的时候,依然会用到上面给大家所讲的tp, fp, fn, tn. 这里会引出另外两个东西, TPR和FPR, 如下:
T P R = t p t p + f n F P R = f p f p + t n \begin{align*} TPR & = \frac{tp}{tp+fn} \\ FPR & = \frac{fp}{fp+tn} \end{align*} TPRFPR=tp+fntp=fp+tnfp
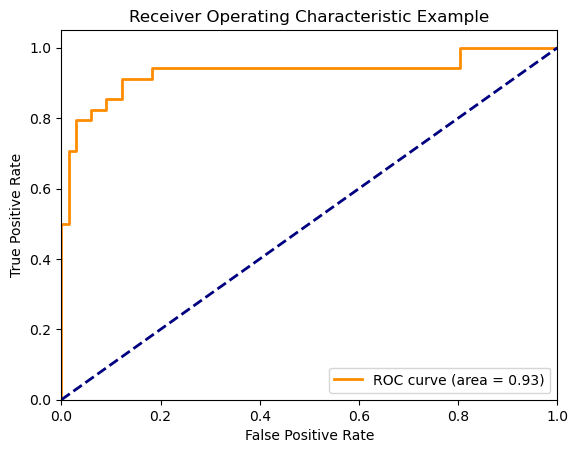
我们来看看咱们之前的这组数据的AUC值:
from sklearn.metrics import roc_curve, aucfpr, tpr, thresholds = roc_curve(true_labels, losses)roc_auc = auc(fpr, tpr)
print('AUC: {}'.format(roc_auc))---
AUC: 0.9300356506238858
下一节课,咱们来说一个非常重要的概念:拟合和欠拟合.
相关文章:

11. 机器学习 - 评价指标2
文章目录 混淆矩阵F-scoreAUC-ROC 更多内容: 茶桁的AI秘籍 Hi, 你好。我是茶桁。 上一节课,咱们讲到了评测指标,并且在文章的最后提到了一个矩阵,我们就从这里开始。 混淆矩阵 在我们实际的工作中,会有一个矩阵&am…...
Nginx的代理和负载均衡
一、nginx的代理方式 1.1 七层代理 七层代理:基于http协议,对请求的内容进行处理,然后转发到后端服务器 七层代理是客户端请求代理服务器,由代理服务器转发客户端的http请求,转发到内部的服务器进行处理(服务器可以是…...

Oracle发布支持Vscode的Java插件
Oracle 发布对 Visual Studio Code 的 Java 插件支持,这个扩展插件通过基于 OpenJDK 的 javac 编译器和调试器接口的语言服务器,为流行的多语言集成开发环境提供 Java 支持。 VS Code 扩展的核心是Java语言服务器:这是一个使用语言服务器协议…...

互联网Java工程师面试题·Java 总结篇·第九弹
目录 75、阐述 JDBC 操作数据库的步骤。 76、Statement 和 PreparedStatement 有什么区别?哪个性 能更好? 77、使用 JDBC 操作数据库时,如何提升读取数据的性能?如何提升更新数据的性能? 78、在进行数据库编程时&a…...
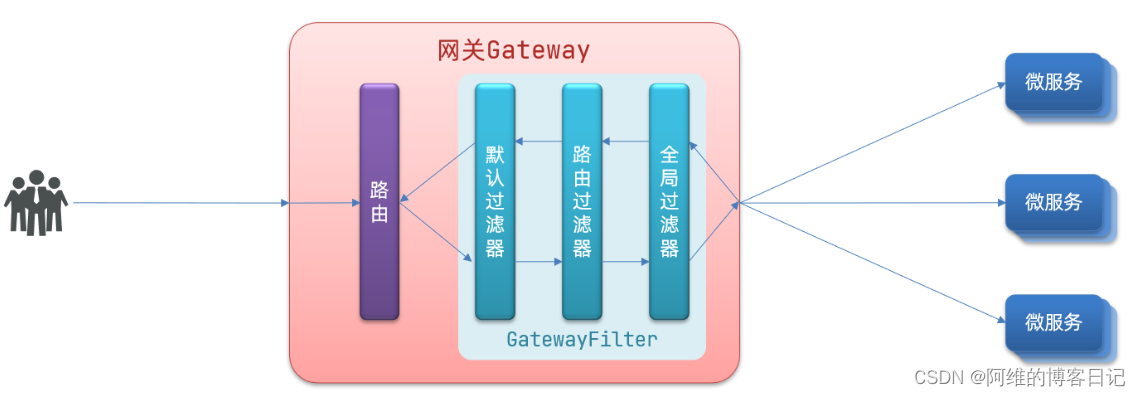
SpringCloud学习笔记-gateway网关自定义全局过滤器
需求:定义全局过滤器,拦截请求,判断请求的参数是否满足下面条件: 参数中是否有authorization, authorization参数值是否为admin 如果同时满足则放行,否则拦截 实现: 在gateway中定义一个过…...
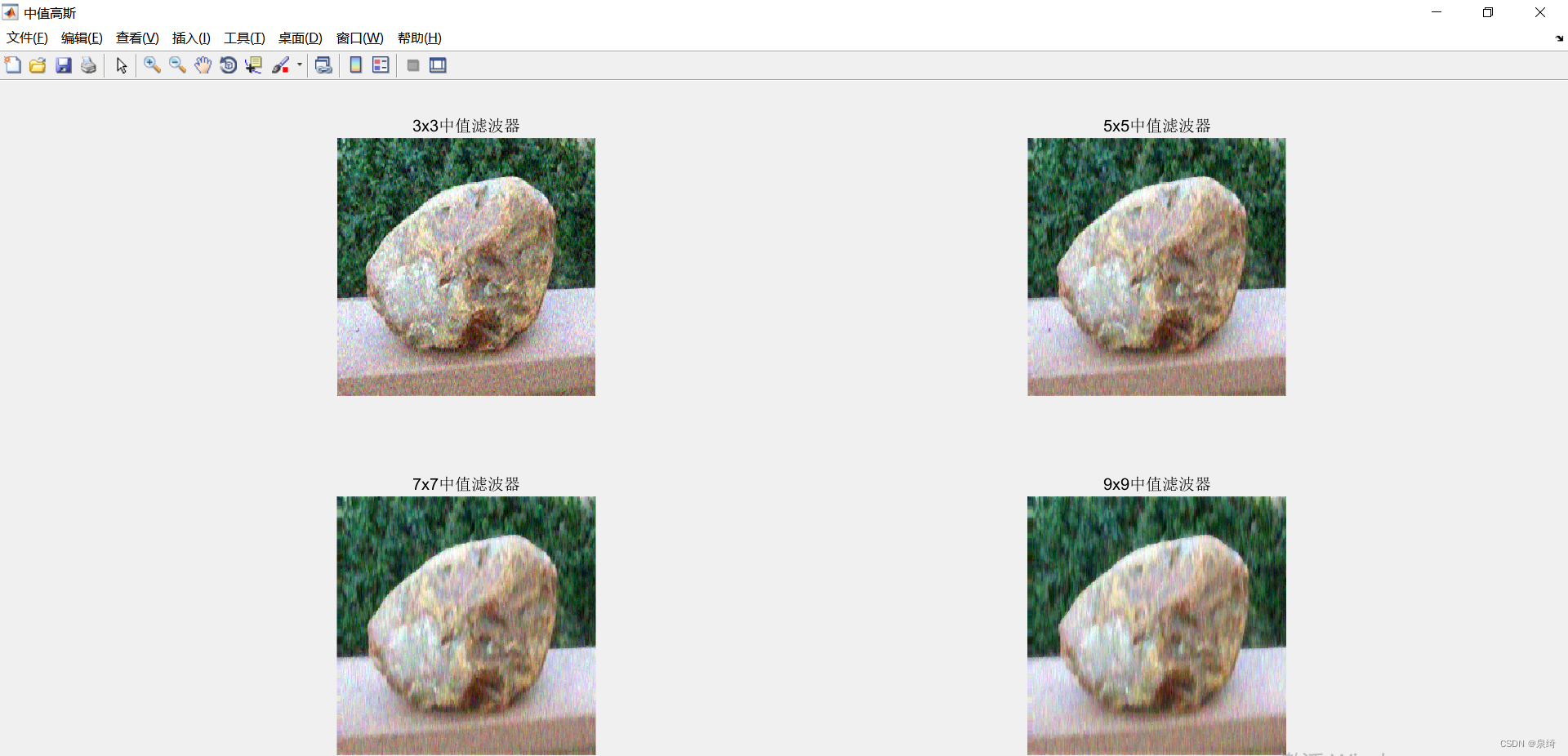
数字图像处理实验记录四(图像的空间域增强-平滑处理)
前言:要是是实验报告赶工的话,建议总结上网抄,或者重构我的总结,仅供学习参考,不要照抄 文章目录 一、基础知识1,噪声2,椒盐噪声3,高斯噪声4,滤波器5,均值滤…...

怎么使用LightPicture开源搭建图片管理系统并远程访问?【搭建私人图床】
文章目录 1.前言2. Lightpicture网站搭建2.1. Lightpicture下载和安装2.2. Lightpicture网页测试2.3.cpolar的安装和注册 3.本地网页发布3.1.Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 现在的手机越来越先进,功能也越来越多,而手机…...
pytorch_神经网络构建4
文章目录 循环神经网络LSTM词嵌入skip-Gram模型N-Gram模型词性预测RNN循环神经网络的基础模块实现RNN识别图片RNN时间序列预测词向量模块词向量运用N-Gram模型lstm词性预测 循环神经网络 这个网络主要用来处理序列信息,之前处理图片时大部分是分析图片的结构信息, 什么是序列信…...
外骨骼机器人和人形机器人概览
前言:一点思考 外骨骼机器人和人形机器人都曾随着一些爆品的出现火热过一段时间,但总感觉当前技术条件还不成熟,真正能落地的应用场景不多。马斯克在擎天柱发布会上被问到人形机器人的落地与前景问题时并没有给出明确答案,只是用…...

Java面试题:链表-反转链表
问题描述 给定一个单链表的头结点pHead(该头节点是有值的,比如在下图,它的val是1),长度为n,反转该链表后,返回新链表的表头。 如当输入链表{1,2,3}时,经反转后,原链表变为{3,2,1},…...
el-upload实现上传文件夹
背景:如图一所示,最下面有一个黄色上传文件按钮,为手动上传而且上传区域有上传文件和上传文件夹的区分 所以需要在点击了上传文件夹做特殊处理使得el-upload可以上传文件夹 一、template区域 <el-uploadclass"upload-file"dra…...

京东数据平台(京东数据分析)2023年9月京东冰箱行业品牌销售排行榜!
鲸参谋监测的京东平台9月份冰箱市场销售数据已出炉! 9月份,大家电行业整体下滑,而冰箱作为大家电市场中的重点品类,受行业趋势变动的影响,冰箱销售市场也同样下滑。鲸参谋数据显示,9月在京东平台上…...

【Excel】WPS单元格快速转换表格字母大小写
使用WPS Office打开表格,选择需要处理的单元格或单元格区域。 依次点击「会员专享」选项卡 —>「智能工具箱」。 再点击「格式」—>「大小写」,选择一种大小写转换方式即可。...
【java】【重构一】分模块开发设计实战
目录 一、创建项目 1、先创建一个空项目 2、设置项目SDK等 二、创建父模块 选择springboot 1、创建父模块parent 2、删除多余文件,只保留pom.xml 3、修改pom.xml 4、将部分公共依赖加入到pom 三、创建实体类子模块entity 1、创建实体类子模块entity 2、…...

Cocos Creator3.8 项目实战(十)使用 protobuf详细教程
在 Cocos Creator 中使用 protobuf.js 库可以方便地进行协议的序列化和反序列化。 下面是使用 protobuf.js 的详细说明: 一、protobuf环境安装 1、安装 npm protobuf环境安装安装需要使用 npm 命令进行,因此首先需要安装 npm 。 如果你还没安装 npm …...
)
第七章:最新版零基础学习 PYTHON 教程—Python 列表(第八节 -在 Python 中获取列表作为用户的输入)
我们经常遇到需要将数字/字符串作为用户输入的情况。在本文中,我们将了解如何使用Python从用户处获取输入列表。 目录 使用Loop在 Python 中获取用户输入的列表 Python3...

Simple RPC - 02 通用高性能序列化和反序列化设计与实现
文章目录 概述设计实现通用的序列化接口通用的序列化实现【推荐】 vs 专用的序列化实现专用序列化接口定义序列化实现 概述 网络传输和序列化这两部分的功能相对来说是非常通用并且独立的,在设计的时候,只要能做到比较好的抽象,这两部的实现…...
简单秒表设计仿真verilog跑表,源码/视频
名称:简单秒表设计仿真 软件:Quartus 语言:Verilog 代码功能: 秒表显示最低计时为10ms,最大为59:99,超出返回00:00 具有复位、启动、暂停三个按键 四个数码管分别显示4个时间数字。 演示…...

【发布】Photoshop ICO 文件格式插件 3.0
备注:本文原文首发于博客园: https://www.cnblogs.com/hoodlum1980/p/17766287.html 【简介】 Photoshop ICO 插件是为 Photoshop 开发的功能扩展插件,使得 Photoshop 可以直接读写 ICO 格式文件。由于 Photoshop 具有强大的像素位图编辑功…...
负载均衡、代理和动静分离的战略
一、Nginx简介 1.1 概述 Nginx (“engine x”) 是一个高性能的 HTTP 和 反向代理服务器,特点是占有内存少,并发能力强,能经受高负载的考验,有报告表明能支持高达 50,000 个并发连接数 。 1.2正向代理与反向代理 1.2.1正向代理 正向代理:如果把局域网外的 Internet 想象…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
