C++三角函数和反三角函数
当涉及到三角函数和反三角函数时,C++提供了一组函数来执行这些计算。以下是C++中常用的三角函数和反三角函数的详细解释和示例说明:
-
sin函数(正弦函数):- 函数原型:
double sin(double x); - 功能:计算给定角度
x的正弦值。 - 返回值:返回
x的正弦值,类型为double。 - 示例:
输出:#include <cmath> #include <iostream>int main() {double angle = 45.0; // 角度值double radians = angle * M_PI / 180.0; // 将角度转换为弧度double result = sin(radians); // 计算正弦值std::cout << "sin(" << angle << ") = " << result << std::endl;return 0; }sin(45) = 0.707107
- 函数原型:
-
cos函数(余弦函数):- 函数原型:
double cos(double x); - 功能:计算给定角度
x的余弦值。 - 返回值:返回
x的余弦值,类型为double。 - 示例:
输出:#include <cmath> #include <iostream>int main() {double angle = 60.0; // 角度值double radians = angle * M_PI / 180.0; // 将角度转换为弧度double result = cos(radians); // 计算余弦值std::cout << "cos(" << angle << ") = " << result << std::endl;return 0; }cos(60) = 0.5
- 函数原型:
-
tan函数(正切函数):- 函数原型:
double tan(double x); - 功能:计算给定角度
x的正切值。 - 返回值:返回
x的正切值,类型为double。 - 示例:
输出:#include <cmath> #include <iostream>int main() {double angle = 30.0; // 角度值double radians = angle * M_PI / 180.0; // 将角度转换为弧度double result = tan(radians); // 计算正切值std::cout << "tan(" << angle << ") = " << result << std::endl;return 0; }tan(30) = 0.57735
- 函数原型:
-
asin函数(反正弦函数):- 函数原型:
double asin(double x); - 功能:计算给定值
x的反正弦值。 - 返回值:返回
x的反正弦值,类型为double。 - 示例:
输出:#include <cmath> #include <iostream>int main() {double value = 0.5; // 值double result = asin(value); // 计算反正弦值std::cout << "asin(" << value << ") = " << result << std::endl;return 0; }asin(0.5) = 0.523599
- 函数原型:
-
acos函数(反余弦函数):- 函数原型:
double acos(double x); - 功能:计算给定值
x的反余弦值。 - 返回值:返回
x的反余弦值,类型为double。 - 示例:
输出:#include <cmath> #include <iostream>int main() {double value = 0.5; // 值double result = acos(value); // 计算反余弦值std::cout << "acos(" << value << ") = " << result << std::endl;return 0; }acos(0.5) = 16. `atan`函数(反正切函数): - 函数原型:
double atan(double x); - 功能:计算给定值
x的反正切值。 - 返回值:返回
x的反正切值,类型为double。 - 示例:
输出:#include <cmath> #include <iostream>int main() {double value = 1.0; // 值double result = atan(value); // 计算反正切值std::cout << "atan(" << value << ") = " << result << std::endl;return 0; }atan(1) = 0.785398
- 函数原型:
这些函数都位于 <cmath> 头文件中,因此需要包含该头文件以在程序中使用它们。这些函数接受弧度或角度作为参数,具体取决于函数的实现。在使用之前,可能需要将角度转换为弧度,例如通过乘以 M_PI/180.0 来将角度转换为弧度。
三角函数的返回值类型为 double,并且它们在处理特殊情况(例如超出定义域的值)时可能返回特殊值,如 NaN(非数字)或正负无穷大。在实际使用中,确保输入的值在定义域范围内,并注意处理可能的异常情况。
相关文章:

C++三角函数和反三角函数
当涉及到三角函数和反三角函数时,C提供了一组函数来执行这些计算。以下是C中常用的三角函数和反三角函数的详细解释和示例说明: sin函数(正弦函数): 函数原型:double sin(double x);功能:计算给…...

Linux篇 五、Ubuntu与Linux板卡建立NFS服务
Linux系列文章目录 一、香橙派Zero2设置开机连接wifi 二、香橙派Zero2获取Linux SDK源码 三、香橙派Zero2搭建Qt环境 四、Linux修改用户名 文章目录 Linux系列文章目录前言一、连接到局域网互ping测试 二、安装NFS服务配置NFS更新exports配置三、板卡安装NFS客户端四、板卡临时…...
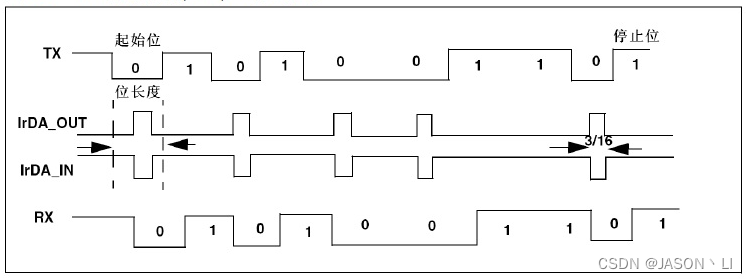
通讯协议学习之路:IrDA协议协议理论
通讯协议之路主要分为两部分,第一部分从理论上面讲解各类协议的通讯原理以及通讯格式,第二部分从具体运用上讲解各类通讯协议的具体应用方法。 后续文章会同时发表在个人博客(jason1016.club)、CSDN;视频会发布在bilibili(UID:399951374) 序、…...
)
互联网摸鱼日报(2023-10-20)
互联网摸鱼日报(2023-10-20) 博客园新闻 OPPO让折叠机超越直板旗舰成为可能 特斯拉的“大空头”,是马斯克那张嘴 逃避内卷的年轻人,盯上了老年大学的音乐课 理想市值超蔚来1倍,一场属于增程式的胜利 补足折叠屏影像短板,OPPO…...
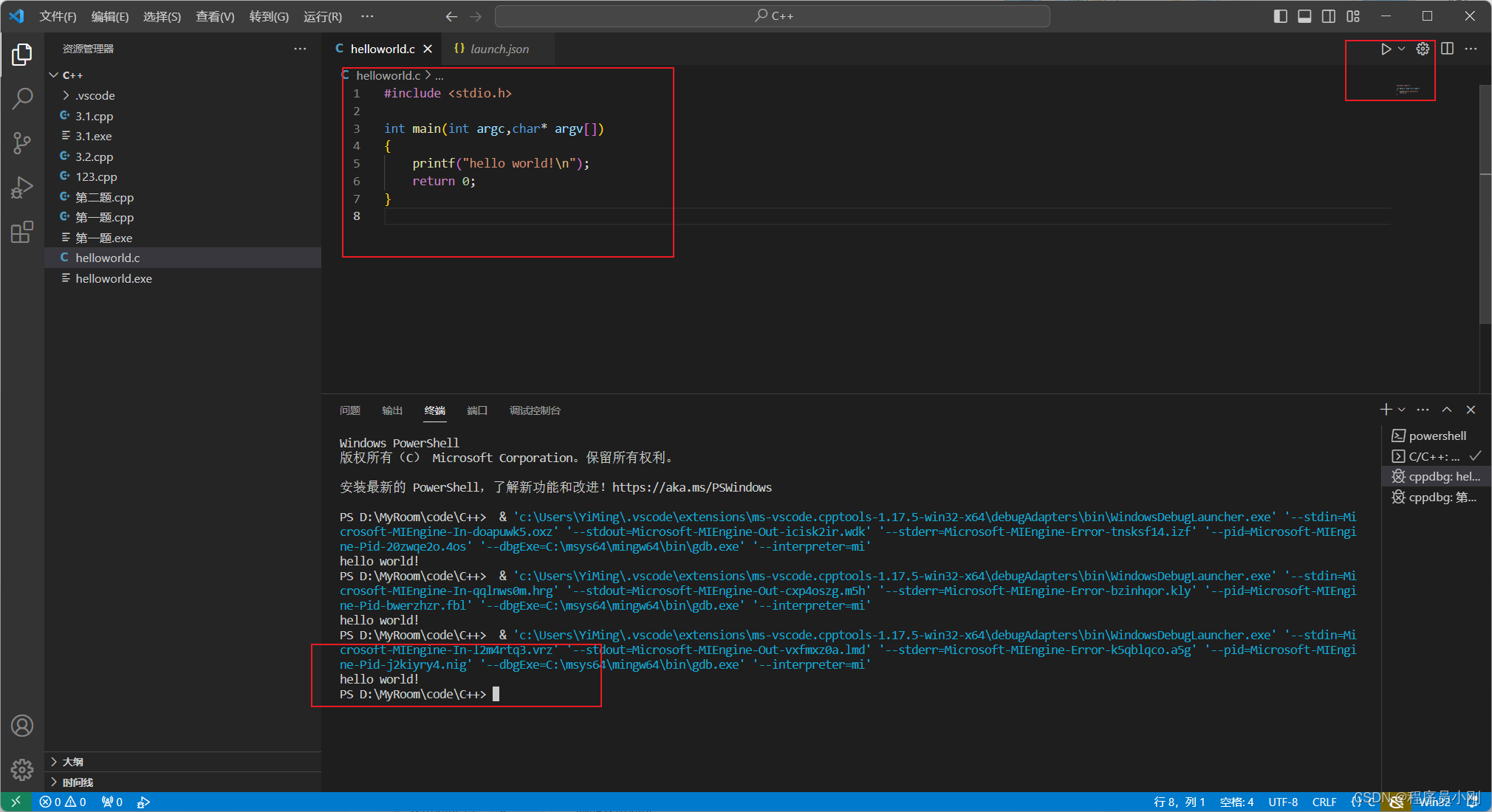
C/C++ 快速入门
参考:https://blog.csdn.net/gao_zhennan/article/details/128769439 1 下载Visual Studio Code并安装中文插件,此处不再叙述 2 插件安装C/C插件 3 使用快捷键【Ctr ~】打打开终端 验证并未安装编译器 4 我们即将使用【MinGW-64】做为编译器 https:…...
【Git】升级MacOS系统,git命令无法使用
终端执行git命令报错 xcrun: error: invalid active developer path (/Library/Developer/CommandLineTools), missing xcrun at: /Library/Developer/CommandLineTools/usr/bin/xcrun安装这个东东,?需要42小时 最终解决: 下载安装 https…...
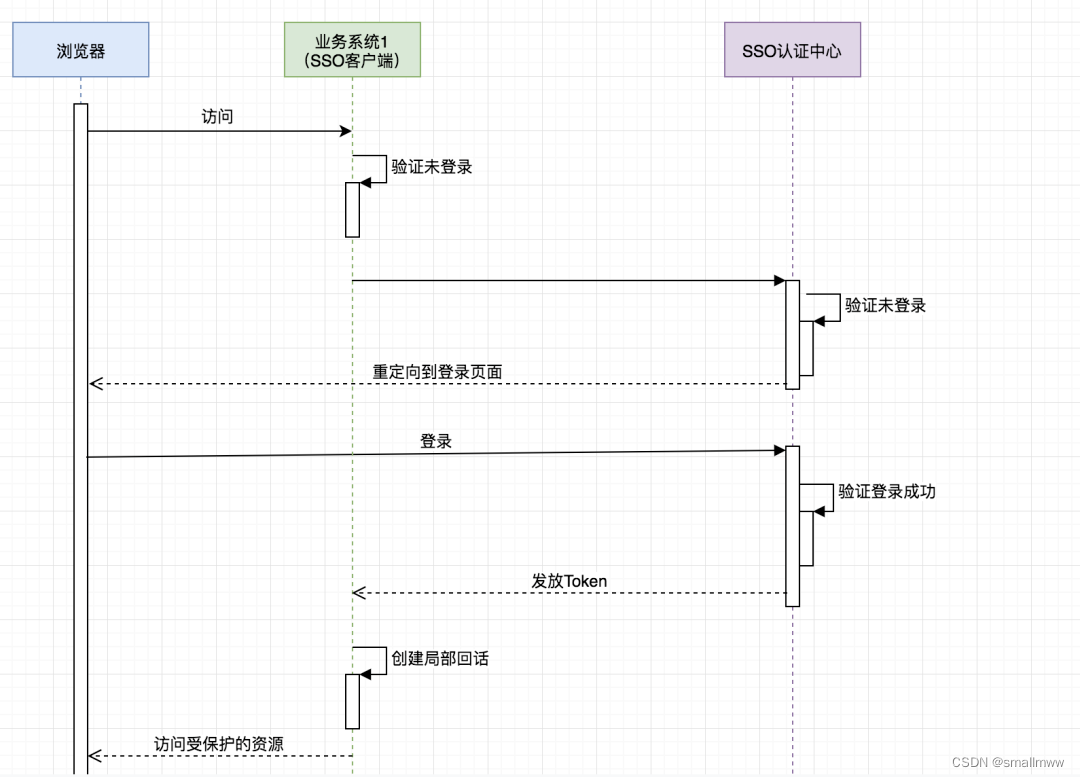
单点登录是什么?
单点登录(Single Sign On, SSO)是指在同一帐号平台下的多个应用系统中,用户只需登录一次,即可访问所有相互信任的应用系统。 单点登录的本质就是在多个应用系统中共享登录状态。如果用户的登录状态是记录在 Session 中的ÿ…...
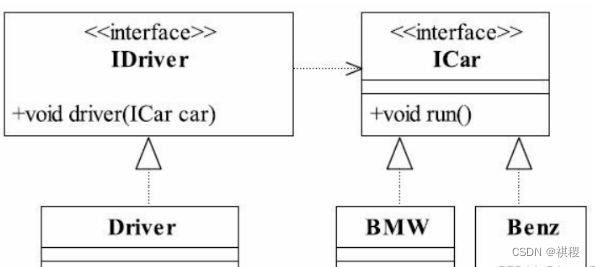
面向对象设计原则之依赖倒置原则
目录 定义原始定义进一步的理解 作用实现方法代码示例 面向对象设计原则之开-闭原则 面向对象设计原则之里式替换原则 面向对象设计原则之依赖倒置原则 面向对象设计原则之单一职责原则 定义 依赖倒置原则(Dependence Inversion Principle),…...

MATLAB——概率神经网络分类问题程序
欢迎关注“电击小子程高兴的MATLAB小屋” %% 概率神经网络 %% 解决分类问题 clear all; close all; P[1:8]; Tc[2 3 1 2 3 2 1 1]; Tind2vec(Tc) %数据类型的转换 netnewpnn(P,T); Ysim(net,P); Ycvec2ind(Y) %转换回来...
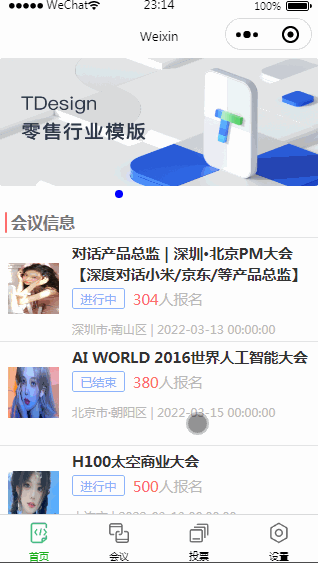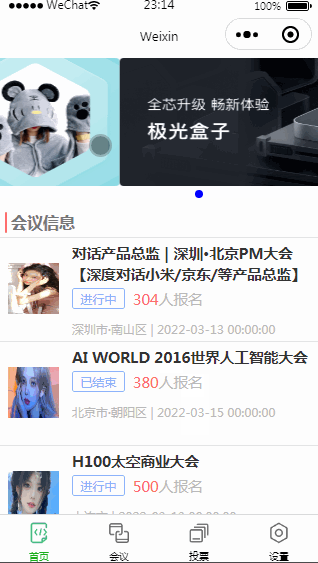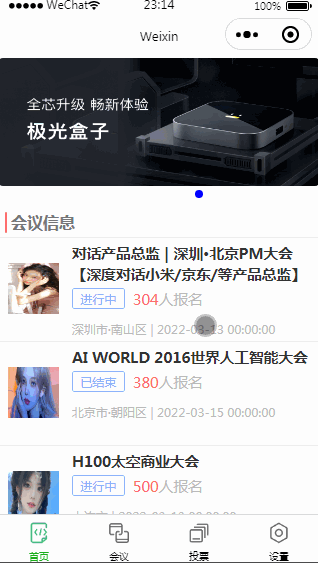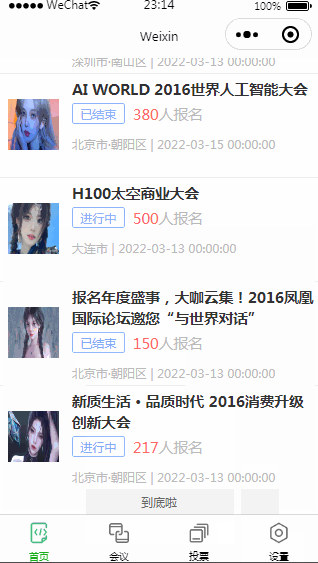
微信小程序的OA会议之首页搭建
目录 一.小程序的布局 1.1. flex是什么 1.2. flex布局 1.3.总体布局 二.轮播图 2.1. 组件 2.2. 数据请求 2.3. 页面 三.首页 2.1. 视图 2.2.数据 2.3. 样式 好啦今天就到这里了,希望能帮到你哦!!! 一.小程序的布局 …...

JS初步了解环境对象this
什么是环境对象? 环境对象:指的是函数内部特殊的变量this,它代表着当前函数运行时所处的环境 作用:弄清楚this的指向,可以让我们代码更简洁 在普通函数中: // 每个函数里面都有this 普通函数的this指向wind…...

Unbuntu-18-network-issue
第六步:容器管理 查看zfs储存卷的占用情况zpool list 为容器修改参数配置 我们不想每个人使用全部的硬件资源,所以还需要限制每个人的参数容器参数配置说明配置容器参数lxc config edit YourContainerName 配置默认容器参数(新容器的参数会…...

Vue、React和小程序中的组件通信:父传子和子传父的应用
序言: 组件化开发是将一个大型应用程序拆分成独立的、可重用的、可组合的模块,使得开发人员可以快速构建和开发应用程序。组件化开发提倡将应用程序的各个功能模块分离开发,每个模块完成自己的功能并且可以在不同的应用程序中被复用。这可以…...

leetcode_171Excel表列序号
1. 题意 把excel中列序号字符串转换为10进制数。 Excel表列序号 2. 题解 26进制转10进制 class Solution { public:int titleToNumber(string columnTitle) {int sz columnTitle.size();int ans 0;int base 1;for ( int i sz - 1; ~i; --i){int v columnTitle[i] - A …...

北斗GPS卫星时钟同步服务器在银行数据机房应用
北斗GPS卫星时钟同步服务器在银行数据机房应用 北斗GPS卫星时钟同步服务器在银行数据机房应用 有些银行、政务、公安等重要业务单位,机房是采用屏蔽保密机房,这种情况下的时钟同步装置方案和普通机房的时钟同步方案又是不一样的。下面我们重点介绍保密机…...
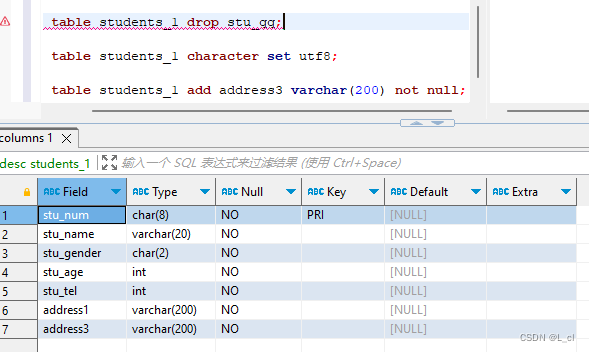
Mysql数据库 1. SQL基础语法和操作
一、Mysql逻辑结构 一个数据库软件可以包含许多数据库 一个数据库包含许多表 一个表中包含许多字段(列) 数据库软件——>数据库——>数据表——>字段(列)、元组(行) 二、SQL语言基础语法 1.SQL…...

ChatGPT-GPT4:将AI技术融入科研、绘图与论文写作的实践
2023年我们进入了AI2.0时代。微软创始人比尔盖茨称ChatGPT的出现有着重大历史意义,不亚于互联网和个人电脑的问世。360创始人周鸿祎认为未来各行各业如果不能搭上这班车,就有可能被淘汰在这个数字化时代,如何能高效地处理文本、文献查阅、PPT…...

SLAM从入门到精通(构建自己的slam包)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 我们学习了很多的开源包,比如hector、gmapping。但其实我们也可以自己编写一个slam包。这么做最大的好处,主要还是可以帮助…...
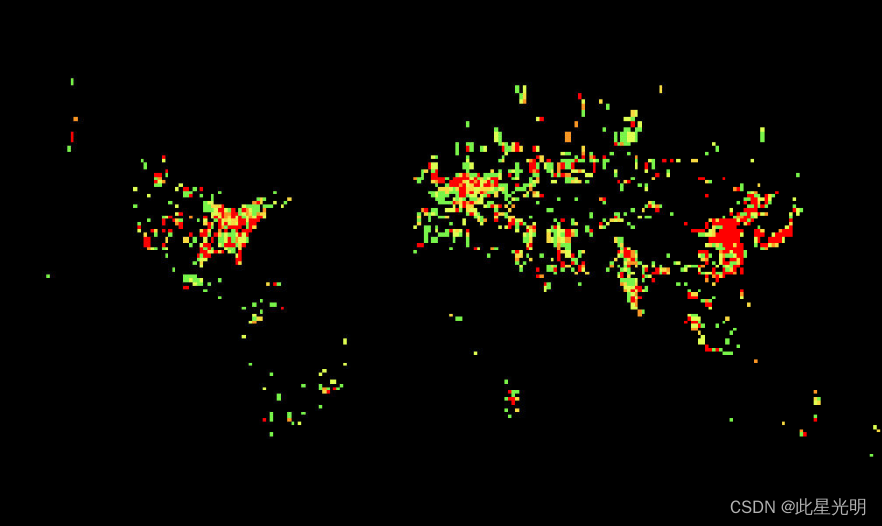
全球二氧化碳排放数据1deg产品(ODIAC)数据
简介 全球二氧化碳排放数据1deg产品(ODIAC)是一个空间分辨率为1deg*1deg的全球化石燃料燃烧产生的二氧化碳空间分布产品。它率先将基于空间的夜间灯光数据与单个发电厂的排放/位置相结合来估计化石燃料二氧化碳的排放。该产品被国际研究界广泛用于各种研究应用(例如…...
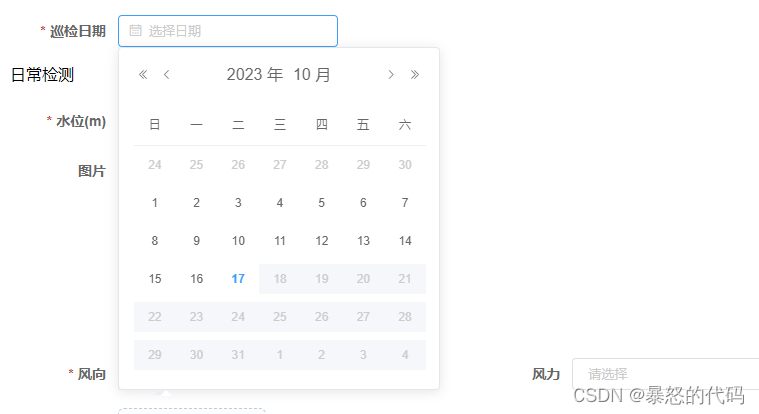
Element-UI 日期选择器--禁用未来日期
在做项目的时候经常会遇到一些报表需要填写日期,一般是填写当日及当日以前,这时候我们的日期选择器就需要进行一些限制,比如: 这样之后,就不会误填写到明天啦,下面让我们看一下代码实现 html页面代码 这里…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
