堆-----数据结构
引言
什么是堆?堆是一种特殊的数据结构(用数组表示的树)。
为什么要使用到堆?比如一场比赛,如果使用擂台赛的方式来决出冠军(实力第一),就很难知道实力第二的队伍是什么了。
但是下图能很清楚的表示各队伍的强弱关系。
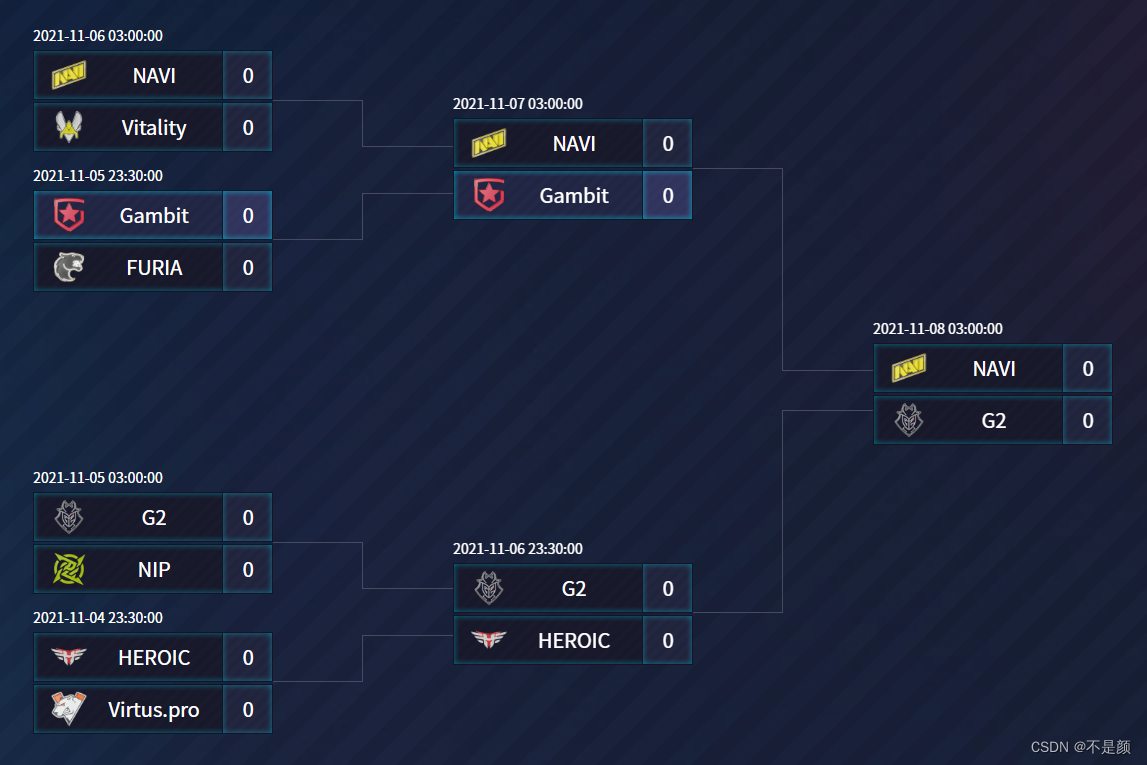
堆的特点
上图就是一个最大堆,解释:每一个圆都是一个节点,数字代表着键值,其中95是93和92的父节点,93和92是95的子节点,93和92是兄弟节点(父节点为同一个),根节点就是键值最大的节点,为95,最后一个节点是87,最后一个左子节点也是87。
最大堆的特点:
满足以下三点
1.每个节点最多可以有两个子节点。
2.根节点的键值是所有堆节点键值中最大者,且每个节点的值都大于其子(孩子)节点。
3.除了根节点没有兄弟节点,最后一个左子节点可以没有兄弟节点,其他节点必须有兄弟节点。
最好是自己理解,不用强记 。其中有一点要注意:A的兄弟节点的子节点可能大于A,相当于在比赛中,其中一个小组都是弱队,那么一个弱队却可以闯入半决赛一样。
最小堆的特点的话就将第二点中的大改为小就可以了,其他的特点一样。这里讨论的是最大堆
数组形式表示
父节点和子节点的关系:
i 的左子节点:2i+1 ,右子节点:2i+2
i 的父节点:(i-1)/2
i 是从 0 开始的
再将上图的堆转换为数组的形式,如下图:

这就是一个最大堆的数组表示形式。
在数组中快速创建堆
也就是怎么把任意一个数组变成最大/小堆。
我们先把堆的最小单位拿出来,如下图:
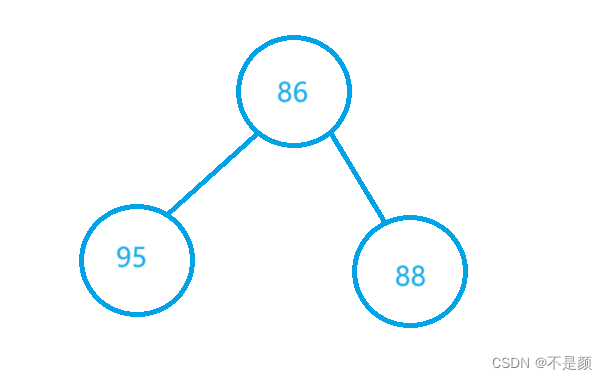
他不是一个最大堆,如果要变成最大堆,只需要父节点是95,子节点分别是86、88就可以了(86和95交换)。而一个最大堆是由若干个这个最小单位组成的,所以第一步就是将所有的堆的最小单位变成最大堆。
1、首先先找到最后一个节点的父节点,找出该节点的最大子节点与自己比较,如果大于自身,就交换两个节点。
2、继续移动到上一个父节点(也就是下标 -1 的地方),重复做第一步的比较操作,直到遍历所有的父节点。
当我们移动完所有的父节点,那最大堆就形成了吗?还疏忽了一个地方。例如当移动到某个父节点时,如下图:
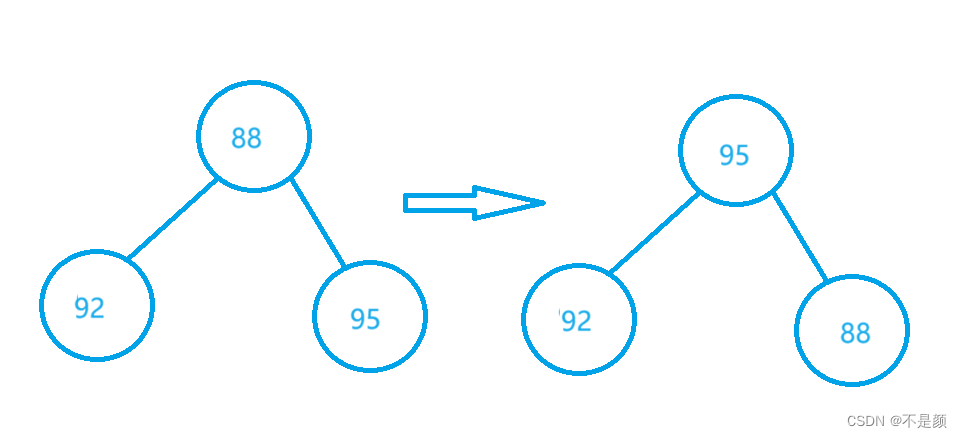
最开始父节点是88,与子节点95交换了,那父节点就是95,95 的子节点就是 88,那88一定大于他的子节点吗?很显然这个答案是不一定,因为 88 的子节点只满足小于之前的父节点 95,所以还需要向下调整,直到子节点都小于父节点。
3、对每次移动中,变成子节点的节点,向下调整,也就是判断他与子节点是否满足最大堆的特点,不满足还要继续移动节点(向下调整),满足的话就接着下个父节点。
4、所有的节点交换完毕,最大堆构建完成。
堆的算法实现
堆数据结构的定义
#define DEFAULT_CAPCITY 120 //默认的堆容量typedef struct _Heap
{int* arr; //存储堆元素的数组int size; //堆中元素的个数int capcity; //堆的容量
}Heap;//函数声明
void buildHeap(Heap& heap);
bool inset(Heap& heap, int value);
bool initHeap(Heap& heap, int* orginal, int size);
void adjustDown(Heap& heap, int i);
void adjustUp(Heap& heap, int i);堆的初始化
bool initHeap(Heap& heap,int *orginal,int size)
{//orginal 是指向数组的指针,而这个数组是我们要传入堆的数组int capcity = DEFAULT_CAPCITY > size ? DEFAULT_CAPCITY : size; //取size和默认容量的最大值heap.arr = new int[capcity];if (!heap.arr) return false; //申请失败heap.capcity = capcity;if (size > 0) //size合法{memcpy(heap.arr, orginal, sizeof(int) * size);heap.size = size;//建堆buildHeap(heap);}return true;
}堆的创建
//建堆,从最后一个父节点逐个向前调整所有的父节点(直到根节点),确保每一个父节点都是一个最大堆
//那么,整体上就是一个最大堆
void buildHeap(Heap& heap)
{int i = (heap.size - 2) / 2; //因为下标从0开始,heap.size-1就得到下标,再结合公式就是这个式子for (; i >= 0; i--){adjustDown(heap, i); //向下调整包含了构建最大堆,如果感到困惑,先看向下调整函数}
}堆的向下调整函数
void adjustDown(Heap& heap, int i)
{int temp = heap.arr[i]; //保存父节点的键值int parent = 0 ,child = 0;for (parent = i; (2 * parent + 1) < heap.size; parent = child) {child = 2 * parent + 1; //先指向左子节点//指向两个子节点中最大的节点if (child + 1 < heap.size && heap.arr[child] < heap.arr[child + 1]){child = child + 1;}if (temp >= heap.arr[child]){break; //无需向下调整}else{heap.arr[parent] = heap.arr[child];heap.arr[child] = temp;}}
}堆的插入新元素
1、插入新的元素到最大堆的尾部,也就是数组的后面
2、插入的元素可能会破环这个最大堆,需要重新调整,和父节点比较,如果比父节点大,就交换两个节点……重复直到新节点比父节点小或者新节点变为根节点(调整到位)。
设计两个函数,一个是插入,一个是向上调整。
bool insert(Heap& heap, int value)
{if (heap.size == heap.capcity) //堆空间不足{return false;}int i = heap.size ; //指向新加元素的下标heap.arr[heap.size++] = value;adjustUp(heap , i);return true;
}void adjustUp(Heap& heap, int i)
{if (i <= 0 || i >= heap.size) return;while (i > 0){int parent = (i - 1) / 2;if (parent >= 0) // 父节点没越界{if (heap.arr[parent] < heap.arr[i]){int temp = heap.arr[i];heap.arr[i] = heap.arr[parent];heap.arr[parent] = temp;i = parent;}else{break; //无需调整}}else{break; //父节点出界}}
}看到这,你会发现堆的创建还有一种方式,也就是将数组的元素一个一个插入,也能得到最大堆。
源代码
#include <iostream>using namespace std;#define DEFAULT_CAPCITY 120 //默认的堆容量typedef struct _Heap
{int* arr; //存储堆元素的数组int size; //堆中元素的个数int capcity; //堆的容量
}Heap;void buildHeap(Heap& heap);
bool insert(Heap& heap, int value);
bool initHeap(Heap& heap, int* orginal, int size);
void adjustDown(Heap& heap, int i);
void adjustUp(Heap& heap, int i);//初始化堆
bool initHeap(Heap& heap,int *orginal,int size)
{//orginal 是指向数组的指针,而这个数组是我们要传入堆的数据int capcity = DEFAULT_CAPCITY > size ? DEFAULT_CAPCITY : size; //取size和默认容量的最大值heap.arr = new int[capcity];if (!heap.arr) return false;heap.capcity = capcity;if (size > 0){memcpy(heap.arr, orginal, sizeof(int) * size);heap.size = size;//建堆buildHeap(heap);}return true;
}//建堆,从最后一个父节点逐个向前调整所有的父节点(直到根节点),确保每一个父节点都是一个最大堆
//那么,整体上就是一个最大堆
void buildHeap(Heap& heap)
{int i = (heap.size - 2) / 2; //因为下标从0开始,heap.size-1就得到下标for (; i >= 0; i--){adjustDown(heap, i);}
}void adjustDown(Heap& heap, int i)
{int temp = heap.arr[i]; //父节点的键值int parent = 0 ,child = 0;for (parent = i; (2 * parent + 1) < heap.size; parent = child){child = 2 * parent + 1;//指向两个子节点中最大的节点if (child + 1 < heap.size && heap.arr[child] < heap.arr[child + 1]){child = child + 1;}if (temp >= heap.arr[child]){break; //无需向下调整}else{heap.arr[parent] = heap.arr[child];heap.arr[child] = temp;}}
}//堆——插入新元素
bool insert(Heap& heap, int value)
{if (heap.size == heap.capcity){return false;}int i = heap.size ;heap.arr[heap.size++] = value;adjustUp(heap , i);return true;
}void adjustUp(Heap& heap, int i)
{if (i <= 0 || i >= heap.size) return;while (i > 0){int parent = (i - 1) / 2;if (parent >= 0) // 父节点没越界{if (heap.arr[parent] < heap.arr[i]){int temp = heap.arr[i];heap.arr[i] = heap.arr[parent];heap.arr[parent] = temp;i = parent;}else{break; //无需调整}}else{break; //父节点出界}}
}
int main(void)
{Heap heap;int orginalArr[] = { 1,2,3,87,93,82,92,86,95 };if (!initHeap(heap, orginalArr, sizeof(orginalArr) / sizeof(int))){cout << "初始化堆失败!" << endl;exit(-1);}for (int i = 0; i < heap.size; i++){printf("%d\n",heap.arr[i]);}puts("");insert(heap, 100);for (int i = 0; i < heap.size; i++){printf("%d\n", heap.arr[i]);}return 0;
}相关文章:

堆-----数据结构
引言 什么是堆?堆是一种特殊的数据结构(用数组表示的树)。 为什么要使用到堆?比如一场比赛,如果使用擂台赛的方式来决出冠军(实力第一),就很难知道实力第二的队伍是什么了。 但是…...

震撼登场 | 拓世科技集团新品亮相成为2023世界VR产业大会全场焦点
在当今世界,新一轮科技革命和产业变革蓬勃发展,虚拟现实作为这一浪潮中的代表性技术,伴随着5G商用及元宇宙概念的迅速兴起,已经成为推动数字经济发展和产业转型升级的关键技术,深刻地改变着人类的生产和生活方式。 10…...

后端接口的查询方式
在与前端对接过程中一直都会遇到一个问题,就是我们后端接口提供好了,自测也通过了,前端却说接口不通,当我们去排查时却发现大都不是接口不通,很多情况是前端使用的姿势不对,比如接口明明写的参数是放到ULR路…...

Maven首次安装配置
所有版本下载地址 http://archive.apache.org/dist/maven/ 配置环境变量 变量名: MAVEN_HOME 值: D:\apache-maven-3.9.5 Path:%MAVEN_HOME%\bin 是否安装成功 mvn -v 出现版本号就安装成功 配置本地仓库 也就是从服务器上下载的JAR包地址&a…...
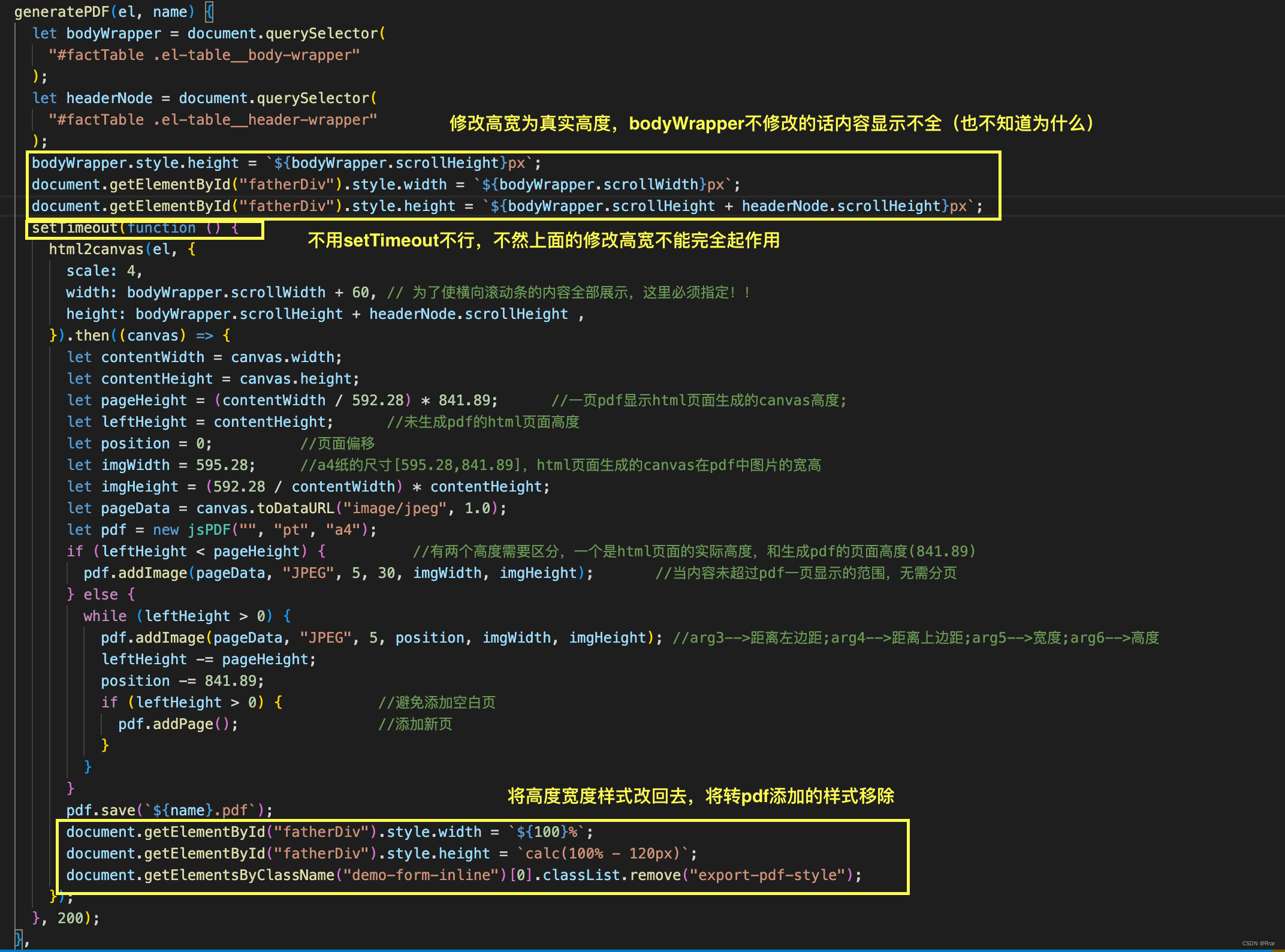
使用html2canvas将html转pdf,由于table表的水平和竖直有滚动条导致显示不全(或者有空白)
结果: 业务:将页面右侧的table打印成想要的格式的pdf,首先遇到的问题是table表上下左右都有滚轮而html2canvas相当于屏幕截图,那滚动区域如何显示出来是个问题? gif有点模糊,但是大致功能可以看出 可复制…...

EDID详解
文章目录 字节含义一些概念YCC位 文章目录 字节含义一些概念YCC位 字节含义 EDID通常由128个字节组成,这些字节提供了关于显示器的各种详细信息。以下是EDID中每个字节位表示的一般含义: Header(头部): 字节0: Headerÿ…...
浅谈云原生
目录 1. 云原生是什么? 2. 云原生四要素 2.1 微服务 2.2 容器化 2.3 DevOps 2.4 持续交付 3. 具体的云原生技术有哪些? 3.1 容器 (Containers) 3.2 微服务 (Microservices) 3.3 服务网格 (Service Meshes) 3.4 不可变基础设施 (Immutable Inf…...
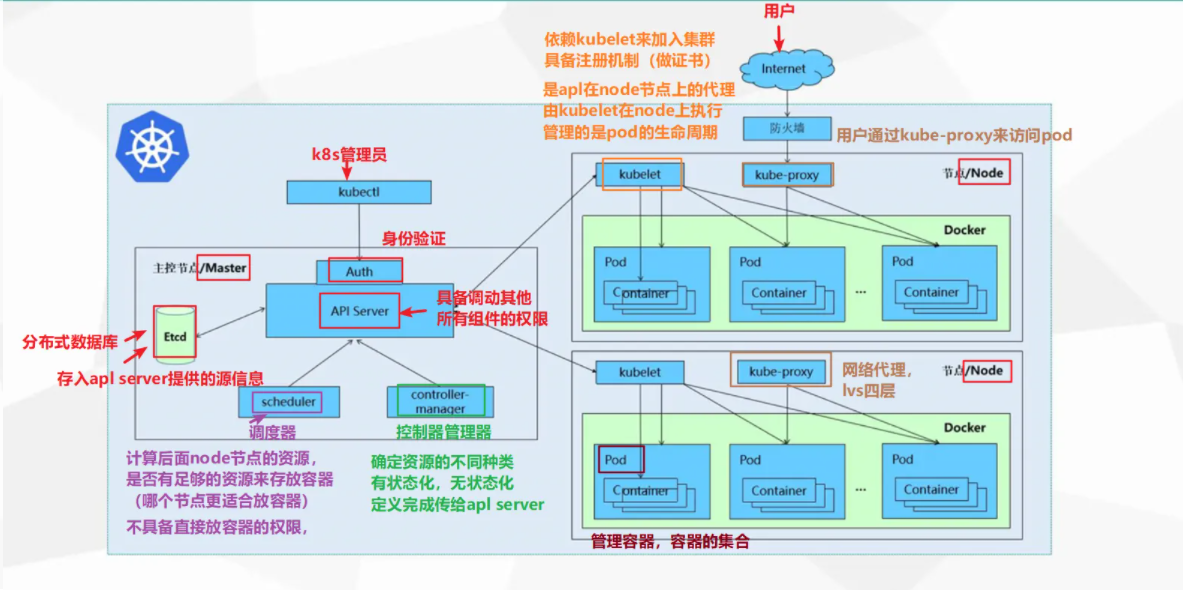
【K8S】Kubernetes
mesos apache基金会,后来是推特公司 mesos分布式资源管理框架2019淘汰 marathon 容器编排框架 用来调度、编排运行的常驻服务 mesos marathon 容器管理 k8s容器或云平台两种趋势(工资好) 1.K8s是什么 K8s全称为 Kubernetesÿ…...

面试题 01.01. 判定字符是否唯一
题目来源: leetcode题目,网址:面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode) 解题思路: 遍历计数即可。 解题代码: class Solution { public:bool isUnique(string astr) {if(astr.l…...

C++(Qt)软件调试---linux使用dmesg定位程序崩溃位置(14)
C(Qt)软件调试—linux使用dmesg定位程序崩溃位置(14) 文章目录 C(Qt)软件调试---linux使用dmesg定位程序崩溃位置(14)1、前言2、ELF文件3、常用工具4、使用dmesg定位异常位置1.1 异常发生在可执行程序中1.2 异常发生在动态库中 1、…...
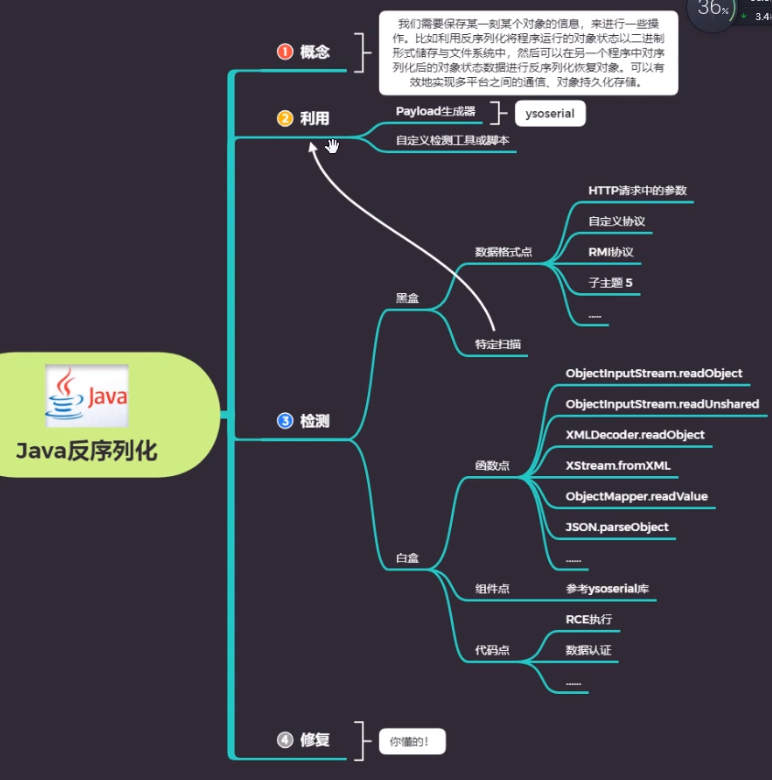
38 WEB漏洞-反序列化之PHPJAVA全解(下)
目录 Java中的API实现序列化和反序列化演示案例WebGoat_Javaweb靶场反序列化测试2020-网鼎杯-朱雀组-Web-think java真题复现 文章参考: https://www.cnblogs.com/zhengna/p/15737517.html https://blog.csdn.net/MCTSOG/article/details/123819548 ysoserial生成攻…...

LeetCode 面试题 10.10. 数字流的秩
文章目录 一、题目二、C# 题解 一、题目 假设你正在读取一串整数。每隔一段时间,你希望能找出数字 x 的秩(小于或等于 x 的值的个数)。请实现数据结构和算法来支持这些操作,也就是说: 实现 track(int x) 方法,每读入一个数字都会调…...

Vue3项目上线打包优化
之前整理过 Vue2项目上线打包优化,在vue3中,使用vite打包,配置稍微改了改。 1 开启gzip压缩 1.1 安装依赖 npm i vite-plugin-compression -D1.2 vite.config.ts 配置 import viteCompression from vite-plugin-compressionexport defaul…...

【算法题】2525. 根据规则将箱子分类
题目: 给你四个整数 length ,width ,height 和 mass ,分别表示一个箱子的三个维度和质量,请你返回一个表示箱子 类别 的字符串。 如果满足以下条件,那么箱子是 “Bulky” 的: 箱子 至少有一个…...

python字典
字典 字典定义创建字典 字典定义 字典是python语言中唯一的映射类型。这种映射类型由键(key)和值(value)组成,是“键值对”的无序可变序列 定义字典时,每个元组的键和值用冒号隔开,相邻元素用…...

thinkphp队列的使用?
1.安装队列依赖 由于框架版本原因可以选择适合的版本 composer require topthink/think-queue 由于我是tp框架5.1的,所以选择了think-queue 1.1.6 composer require topthink/think-queue 1.1.6 判断安装成功 php think queue:work -h image.png 2.配置文件…...
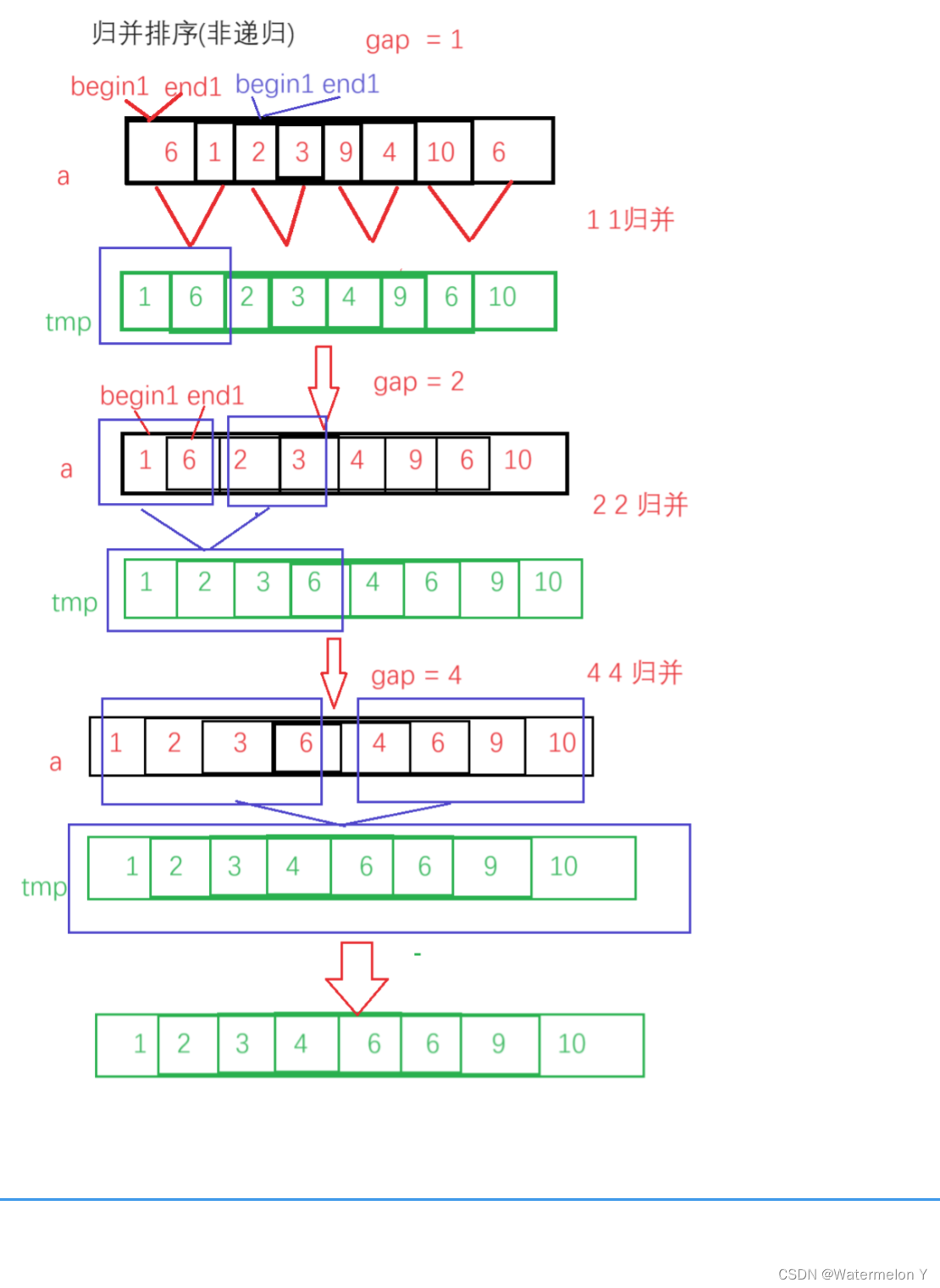
【数据结构】排序--归并排序
目录 一 基本思想 二 代码实现 三 非递归归并排序 一 基本思想 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并ÿ…...
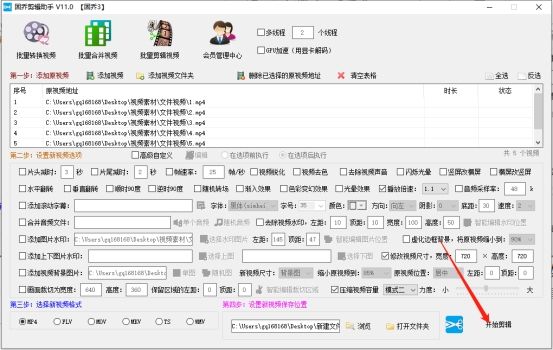
批量修改视频尺寸:简单易用的视频剪辑软件教程
如果你需要批量修改视频尺寸,同时保持高质量的画质,那么“固乔剪辑助手”这款软件是你的不二之选。下面就是如何使用这款软件进行批量修改视频尺寸的详细步骤。 1. 首先,你需要在浏览器中进入“固乔科技”的官网,然后下载并安装“…...

四川云汇优想:短视频矩阵运营方案
短视频矩阵运营方案是为了提高短视频平台的用户黏性和活跃度,从而增强用户粘性和平台的商业价值而制定的。下面四川百幕晟小编将对短视频矩阵运营方案进行详细的介绍和分析。 首先,短视频矩阵运营方案要注重用户精细化运营。通过用户画像和兴趣标签&…...

vue中如何获取到当前位置的天气
要在Vue中获取当前位置的天气,您需要使用浏览器的Geolocation API来获取设备的地理位置,并使用第三方的天气API来获取天气数据。 下面是一般的步骤: 在Vue项目中安装axios库,用于发送HTTP请求。 npm install axios 创建一个新的…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

