数据结构-堆排序Java实现
目录
- 一、引言
- 二、算法步骤
- 三、原理演示
- 步骤1: 构建最大堆
- 步骤2: 交换和堆化
- 步骤3: 排序完成
- 四、代码实战
- 五、结论
一、引言
堆排序是一种利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
二、算法步骤
堆排序的核心是建立和维护一个二叉堆,通常是一个最大堆(Max Heap)或最小堆(Min Heap)。在最大堆中,根节点的值是最大的,而在最小堆中,根节点的值是最小的。堆排序的基本思路如下:
- 构建最大堆:将未排序的数组构建成一个最大堆。这通常需要从最后一个非叶子节点开始,逐步向前调整,使整个数组满足最大堆的性质。
- 交换和堆化:将最大堆的根节点与最后一个元素交换,然后减小堆的大小(即排除最后一个元素),再对根节点进行堆化操作,以保持最大堆的性质。
- 重复步骤2:重复执行步骤2,直到堆的大小减小到1,排序完成。
三、原理演示
堆排序是一种基于二叉堆数据结构的排序算法,它通过构建和维护一个最大堆(或最小堆)来对数组进行排序。在这里,我将动态说明堆排序的实现过程,以帮助您更好地理解它。
步骤1: 构建最大堆
假设我们有一个未排序的整数数组作为输入。第一步是将这个数组构建成一个最大堆,确保堆的性质:每个父节点的值都大于或等于其子节点的值。初始数组:
[4, 10, 3, 5, 1]
构建最大堆的过程:
从数组的中间元素开始,即索引为 n/2 - 1,这是最后一个非叶子节点。从这个节点向前遍历,执行堆化操作。
[4, 10, 3, 5, 1]
堆化过程:从根节点开始,比较它与其子节点的值,如果子节点的值更大,则交换它们,然后继续堆化子节点。
[10, 4, 3, 5, 1]
继续堆化直到整个数组成为最大堆。
步骤2: 交换和堆化
在第一步完成后,我们已经构建了一个最大堆,其中根节点包含最大的元素。现在,我们将根节点与最后一个元素交换,将最大元素放到正确的位置。交换和堆化的过程:
交换根节点和最后一个元素:
[1, 4, 3, 5, 10]
减小堆的大小,排除最后一个元素。
对根节点进行堆化操作,以保持最大堆性质。
[5, 4, 3, 1]
重复步骤1和步骤2,直到堆的大小减小到1,排序完成。
步骤3: 排序完成
最终,堆排序完成,数组中的元素按升序排列。
排序完成的数组:
[1, 3, 4, 5, 10]
这就是堆排序的整个过程。它的时间复杂度为O(nlogn),具有稳定性,适用于大型数据集的排序。堆排序的核心是构建和维护堆,确保最大(或最小)元素位于根节点,然后将根节点与数组末尾的元素交换,并逐渐减小堆的大小。
四、代码实战
下面我们使用java演示一下堆排序的过程:
public class HeapSort {public static void main(String[] args) {int[] arr = {12, 11, 13, 5, 6, 7};int n = arr.length;System.out.println("原始数组:");printArray(arr);heapSort(arr);System.out.println("排序后的数组:");printArray(arr);}public static void heapSort(int[] arr) {int n = arr.length;// 构建最大堆for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}// 逐个提取元素并排序for (int i = n - 1; i >= 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;heapify(arr, i, 0);}}public static void heapify(int[] arr, int n, int i) {int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left < n && arr[left] > arr[largest]) {largest = left;}if (right < n && arr[right] > arr[largest]) {largest = right;}if (largest != i) {int swap = arr[i];arr[i] = arr[largest];arr[largest] = swap;heapify(arr, n, largest);}}public static void printArray(int[] arr) {for (int value : arr) {System.out.print(value + " ");}System.out.println();}
}
上述代码演示了堆排序的实现。它首先定义了一个包含整数数组的示例,然后调用 heapSort 方法来对数组进行排序。heapSort 方法首先构建一个最大堆,然后进行排序。heapify 方法用于维护最大堆的性质。
五、结论
我们一起来总结一下:
- 堆排序是一种选择排序的变种,它将待排序序列划分成若干个子序列,每个子序列都满足堆积的性质,即子序列的最大值(或最小值)位于其顶部。
- 堆排序的时间复杂度为O(nlogn),其中n表示待排序序列的长度。这是因为堆排序需要将序列构造成堆,这需要O(nlogn)的时间复杂度,然后需要依次取出每个元素,这需要O(n)的时间复杂度。
- 堆排序的空间复杂度为O(1)。这是因为堆排序只需要在内存中使用常数级别的额外空间来完成排序。
- 堆排序是原地排序算法,也就是说,它不需要额外的存储空间,除了用于存储待排序序列本身的存储空间之外。
- 堆排序是稳定的排序算法,也就是说,它保持了相同元素的相对顺序。
- 堆排序适用于大规模数据的排序,特别是当内存空间有限时,因为它只需要常数级别的额外空间。
- 堆排序算法的实现比较简单,但理解和掌握它需要对数据结构和算法有较深入的理解。
点赞收藏,富婆包养✋✋
相关文章:

数据结构-堆排序Java实现
目录 一、引言二、算法步骤三、原理演示步骤1: 构建最大堆步骤2: 交换和堆化步骤3: 排序完成 四、代码实战五、结论 一、引言 堆排序是一种利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或…...
C#进阶——反射(Reflection)
定义:反射指的是在运行时动态地获取、检查和操作程序中的类型信息,而在我们的Unity中反射允许开发者在运行时通过代码来访问和修改对象的属性、方法和字段,而不需要提前知道这些成员的具体信息。 举一个例子,我们使用反射在运行的…...

Oracle 运维篇+应用容器数据库的install、upgrade、patch、uninstall
★ 知识点 ※ DEFAULT_SHARING参数的取值 METADATA: 元数据链接共享数据库对象的元数据,但其数据对于每个容器是唯一的。这些数据库对象被称为元数据链接的应用程序公共对象。此设置为默认设置。DATA: 数据链接共享数据库对象,其数据对于应用程序容器中…...
Affinity Publisher for Mac/Windows最新中文下载 排版神器
Affinity Publisher是一款专业的排版和设计软件,它可以帮助您从简单的文档到复杂的书籍和杂志轻松创建高质量的出版物。 该软件具有直观的界面和强大的功能,使您可以轻松组织和编辑文本、图像和数据,并创建令人惊叹的布局。 Affinity Publi…...
Mac文件对比同步工具 Beyond Compare 4.4.7
Beyond Compare 4 是一款强大的文件和文件夹比较工具。它提供了一个直观的界面,使您可以快速比较和同步文件和文件夹。 Beyond Compare 4 具有许多有用的功能,包括比较和合并文件、文件夹和压缩文件,以及同步文件和文件夹。它支持各种类型的文…...
技巧 | 如何解决 OBS 系统声音无法捕获问题 | Mac
技巧 | 如何解决 OBS 系统声音无法捕获问题 | Mac 问题描述 由于 macOS 系统限制,桌面音频被禁止,导致在使用 OBS 无法录制桌面音频,只能使用自带麦克风录制。 解决方法 Loopback 介绍 借助 Loopback 的强大功能,可以轻松地…...
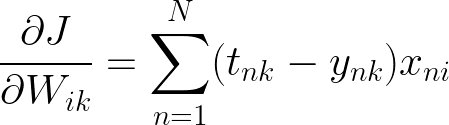
从头开始机器学习:逻辑回归
一、说明 本篇实现线性回归的先决知识是:基本线性代数,微积分(偏导数)、梯度和、Python (NumPy);从线性方程入手,逐渐理解线性回归预测问题。 二、逻辑回归简介 我们将以我们在线性回…...

插入排序 算法
从第二个开始,从后面往前找,如果比其小,就交换,else 就终止 for i 1 i <n i for j i j > 0 (到第二个) j-- if < swap 下面给出源码 //对插入排序来说,直接从第二个元素开始template<ty…...
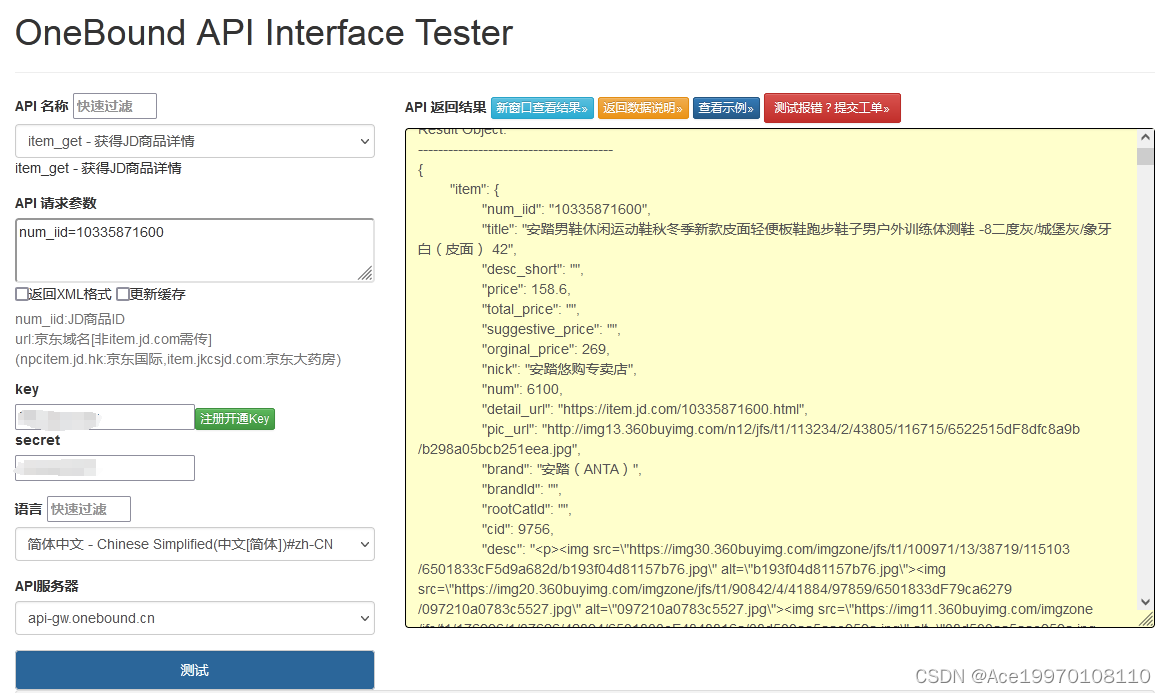
“揭秘!如何通过京东商品详情接口轻松获取海量精准商品信息!“
京东商品详情接口可以通过HTTP GET请求获取商品详情信息。 请求参数包括num_iid,表示JD商品ID。 请求示例: GET /jd/item_get/?num_iid10335871600 HTTP/1.1 Host: api-vx.Taobaoapi2014.cn Connection: close Accept-Encoding: gzip 点击获取…...

已经有多人中招,不要被AI换脸技术骗了!
您好,我是码农飞哥(wei158556),感谢您阅读本文,欢迎一键三连哦。 💪🏻 1. Python基础专栏,基础知识一网打尽,9.9元买不了吃亏,买不了上当。 Python从入门到精…...

solidworks 2024新功能之--保存为低版本 硕迪科技
大家期盼已久的SOLIDWORKS保存低版本文件功能来了,从SOLIDWORKS 2024 开始,您可以将在最新版本的SOLIDWORKS 中创建的SOLIDWORKS零件、装配体和工程图另存为SOLIDWORKS 早期版本的全功能文档(完成的特征树与相关参数)。 将文件另…...
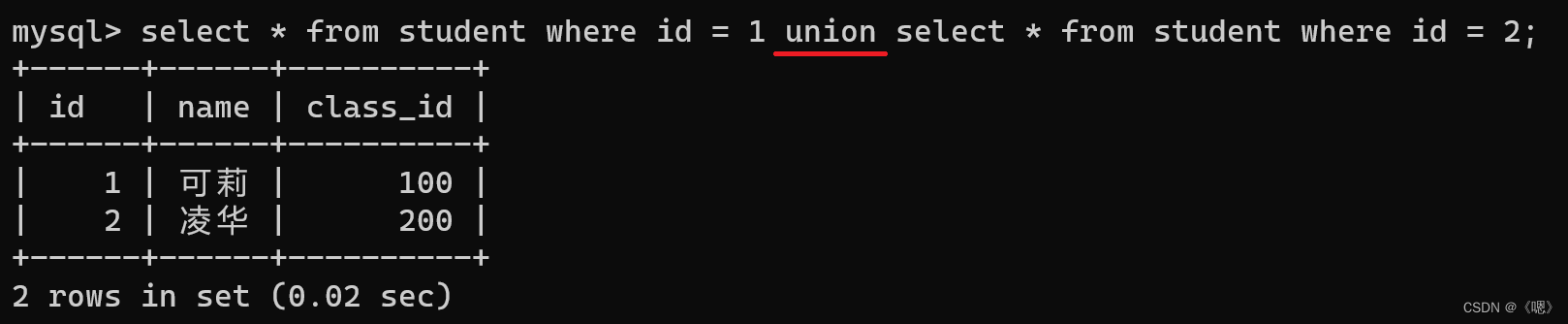
MySQL --- 聚合查询 和 联合查询
聚合查询: 下文中的所有聚合查询的示例操作都是基于此表: 聚合函数 聚合函数都是行与行之间的运算。 count() select count(列名) from 表名; 统计该表中该列的行数,但是 null 值不会统计在内,但是如果写为 count(*) 那么 nu…...
Note——torch.size() umr_maximum() array.max() itertools.product()
torch.size Problem TypeError: ‘torch.Size’ object is not callable Reason Analysis torch.Size函数不可调用 因为torch只可以.size() 或 shape Solution 将y.shape()替换为y.size() 或 y.shape ytorch.normal(0,0.01,y.size())2 return umr_maximum(a, axis, None…...

python学习笔记6-DefaultDict
对于一般的字典来说,如果键不存在会导致【KeyError】,因此可以考虑用DefaultDict # Defining the dict d defaultdict(def_value) d["a"] 1 d["b"] 2print(d["a"]) print(d["b"]) print(d["c"…...

Redis 底层对 String 的 3 个优化
Redis对 String 类型实现了很多优化,通过以下三个重要的优化点来解释: 1. 简单动态字符串(SDS) Redis 的 String 类型内部采用简单动态字符串(SDS)来管理字符串。相比于 C 语言的原生字符串,S…...
简约艺术签名小程序源码/流量主小程序源码/字节跳动抖音小程序
源码简介: 本源码为简约艺术签名小程序、流量主小程序以及字节跳动抖音小程序的源代码。该小程序是一款实用的工具,旨在帮助用户创建各种独特的艺术签名,以便在社交媒体平台上更好地展示用户的个性和创意。 源码链接: 网盘源码 …...
挂载iso文件和配置apt本地源)
Ubuntu(kylin)挂载iso文件和配置apt本地源
版本说明:Ubuntu Server 16.04 LTS解决问题:解决在无任何互联网的环境下,安装软件时缺少依赖包的问题 方法一:通过虚拟机挂载 将镜像挂载到虚拟机以VMware Workstation为例,打开“虚拟机设置”,点击“CD/DVD”选项,将 “设备状态”中的“<...

wps表格求标准差怎么算?
在WPS表格中,要计算标准差,可以使用STDEV函数。标准差是一种衡量数据集合离散程度的统计指标。下面我将详细介绍如何使用STDEV函数来计算标准差。 STDEV函数的语法为:STDEV(range) 其中,range表示要计算标准差的数据范围&#x…...

安达发|制造企业生产排产现状和APS系统的解决方案
随着市场竞争的加剧,制造业企业面临着生产效率、成本控制和客户满意度等方面的巟大压力。在这种背景下,生产排产作为制造业的核心环节,对企业的生产经营具有重要意义。本文将针对制造业的生产排产现状进行分析,并提出相应的APS系统…...
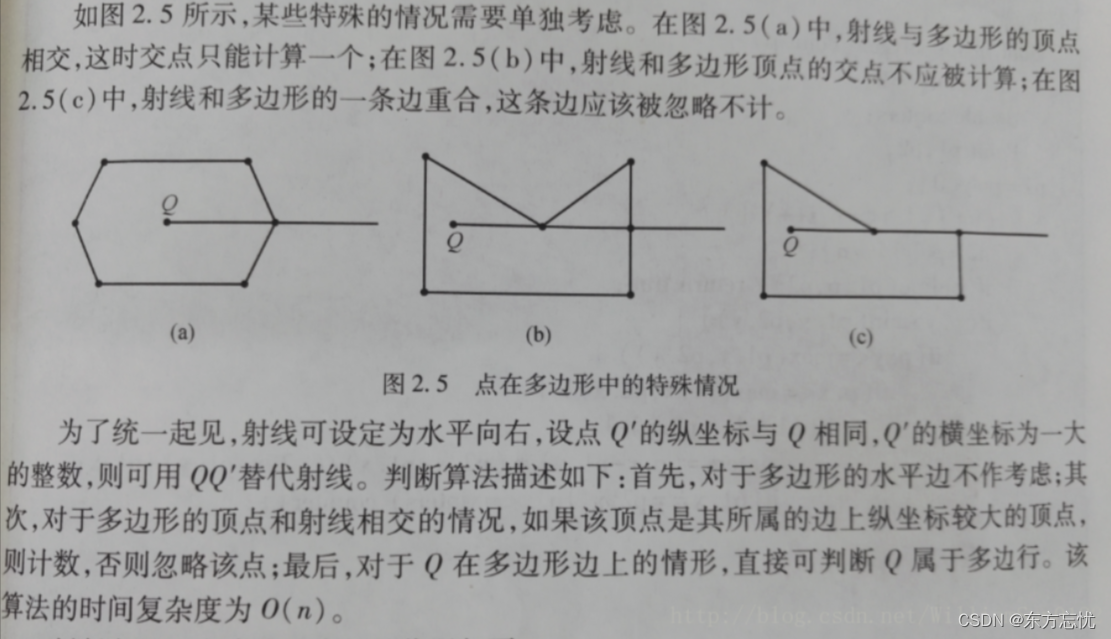
Qt判断一个点在多边形内还是外(支持凸边形和凹变形)
这里实现的方法是转载于https://blog.csdn.net/trj14/article/details/43190653和https://blog.csdn.net/WilliamSun0122/article/details/77994526 来实现的,并且按照Qt的规则进行了调整。 以下实现方法有四种,每种方法的具体讲解在转载的博客中有说明&…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
