C语言求解汉诺塔问题
完整代码:
/*Hanoi(汉诺)塔问题。这是一个古典的数学问题:古代有一个梵塔,塔内有 3 个 座 A,B,C,开始时 A 座上有 64 个盘子,盘子大小不等,大的在下,小的在上。有一个老
和尚想把这 64 个盘子从 A 座移到 C 座,但每次只允许移动一个盘子,且在移动过
程中在 3 个座上都始终保持大盘在下,小盘在上。在移动过程中可以利用 B 座,要
求编程序打印出移动的步骤。*/
#include<stdio.h>//n为汉诺塔的层数,a为初始柱,b为辅助柱,c为目标柱
void Hanoi(int n,char a,char b,char c){//当只有一层时,直接把a柱的盘子移到c柱if (n==1){printf("%c->%c\n",a,c);}else{//借助c柱,让a柱的盘子移动到b柱Hanoi(n-1,a,c,b);//因为此时移动到b柱上有n-1层,此时a柱上还剩一个最大的盘子//让最大的盘子从a柱移动到c柱Hanoi(1,a,b,c);//此时问题就变成了把b柱上所有盘子(n-1个)借助a柱移动到c柱Hanoi(n-1,b,a,c);}
}
int main()
{int n;printf("请输入初始时盘子个数:\n");scanf("%d",&n);Hanoi(n,'A','B','C');return 0;
}
运行截图:
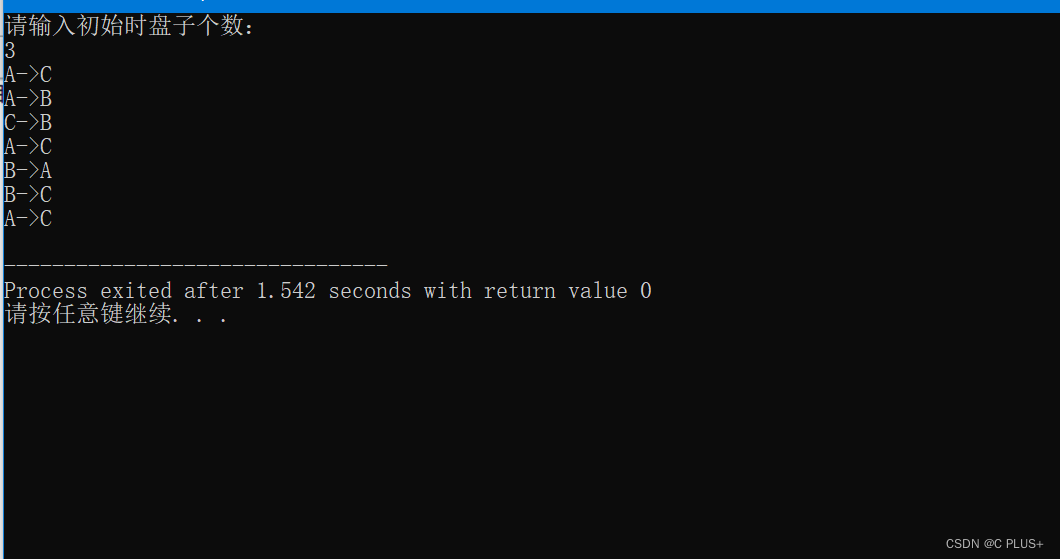
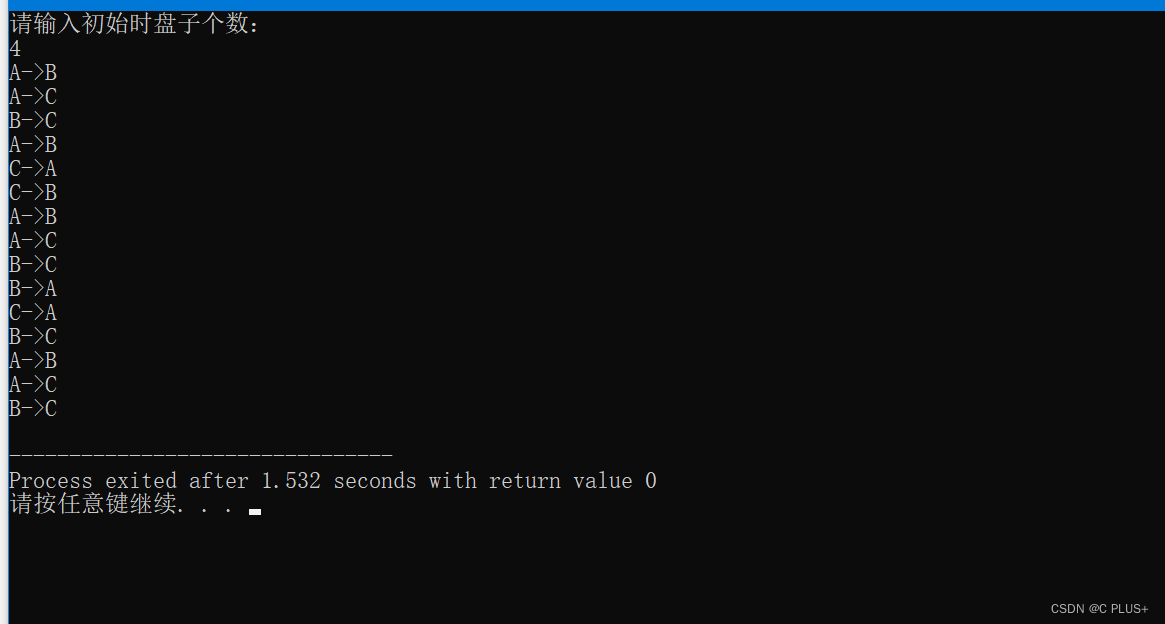
相关文章:

C语言求解汉诺塔问题
完整代码: /*Hanoi(汉诺)塔问题。这是一个古典的数学问题:古代有一个梵塔,塔内有 3 个 座 A,B,C,开始时 A 座上有 64 个盘子,盘子大小不等,大的在下,小的在上。有一个老…...
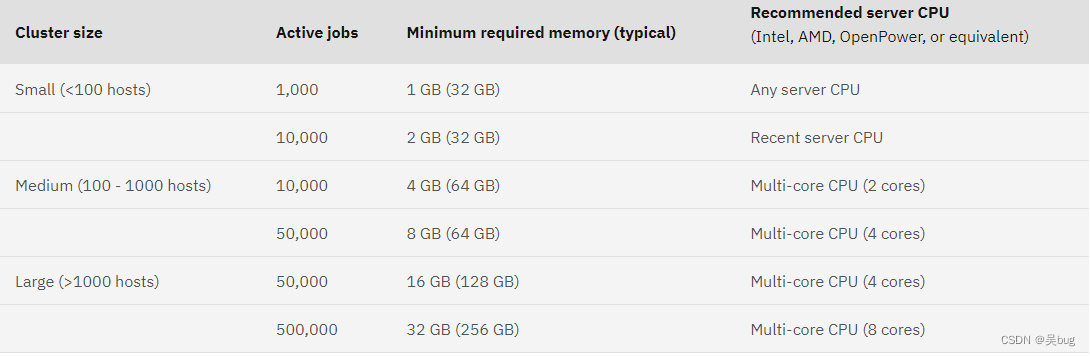
安装LSF
安装需求 基本硬件配置建议: CPU 4核或以上(LSF 没有最低 CPU 需求,此处只是建议)内存 8G或以上( 当没有作业在运行时, Linux x86-64 上集群中的 LSF 守护程序将使用大约 488 MB 内存。)交换…...

百度的新想象力在哪?
理解中国大模型,百度是一个窗口。这个窗口的特殊性不仅在于变化本身,而是在于百度本身就是那个窗口。 作者|皮爷 出品|产业家 沿着首钢园北区向西北步行10分钟,就能看到一个高约90米的大跳台,在工业园钢铁痕迹的印衬下&#…...
Linux使用rpm包安装mysql5.7
以前安装过mysql 前言:检查以前是否装有mysql rpm -qa|grep -i mysql安装了会显示: bt-mysql57-5.7.31-1.el7.x86_64 停止mysql服务和删除之前安装的mysql rpm -e bt-mysql57-5.7.31-1.el7.x86_64查找并删除mysql相关目录 find / -name mysql/va…...

LLDB 三种输出方式 对比及原理探索
前言 当我们的项目过大时,就会使我们项目的编译耗时过长,如何在项目运行时进项代码调试,熟练使用LLDB就可以解决这个难题,大幅度提高我们的开发效率。 什么是 LLDB? LLDB是英文Low Lever Debug的缩写,是XCode内置的为我们开发者提供的调试工具,它与LLVM编译器一起,存…...
)
基于架构软件设计-架构真题(五十八)
“41”视图主要描述系统逻辑架构。其中()视图用于描述对象模型,并说明系统应该为用户提供哪些服务。 过程开发物理逻辑 解析: “41”有逻辑视图、过程视图、物理视图、开发视图和架构的描述。 逻辑视图:设计的对象…...
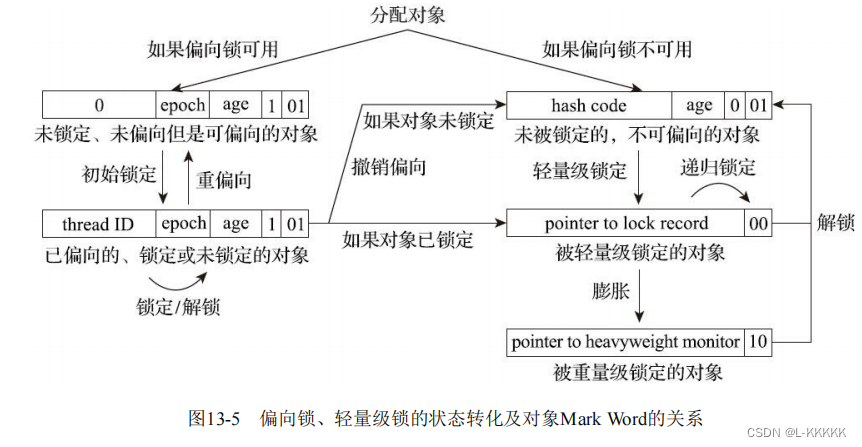
jvm实现的锁优化
目录 轻量级锁 轻量级锁的工作流程 轻量级锁的解锁 偏向锁 偏向锁的流程: 偏向锁和轻量级锁机区别: 其他优化 自旋锁和自适应自旋锁 锁消除 锁粗化 轻量级锁 “轻量级” 是相对于使用操作系统互斥量来实现的传统锁而言的,因此传统的…...
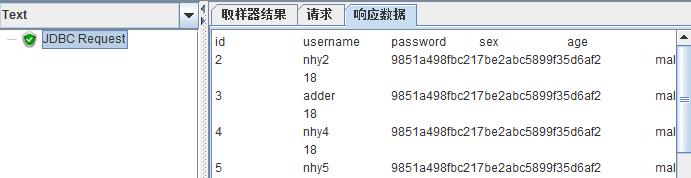
JMeter做http接口功能测试
1. 普通的以key-value传参的get请求 e.g. 获取用户信息 添加http请求;填写服务器域名或IP;方法选GET;填写路径;添加参数;运行并查看结果。 2. 以Json串传参的post请求 e.g. 获取用户余额 添加http请求;…...

【安全体系架构】——SIEM架构
什么是SIEM架构? 安全信息与事件管理(SIEM)架构是一种综合性的安全管理系统,旨在监控、检测、报告和应对安全事件和威胁。SIEM系统集成了多个安全功能,包括日志收集、事件管理、威胁检测和响应,以提供组织…...

nginx acess日志找不到访问记录问题
这个是AI给出的可能得原因: 如果在nginx中找不到你的访问记录,但你确实进行了访问并得到了返回,可能有以下原因: 日志文件位置设置不正确:请确保你的nginx配置文件中的access_log指令指向了正确的日志文件路径。日志文…...

canvas使用
canvas使用 1 canvas绘制基本 1 概念 HTML5<canvas>元素用于图形的绘制,区别于css,它的绘制通过javascript来完成绘制的 <canvas>标签只是图形容器,必须使用及保本来绘制图形 Canvas API主要聚焦与2D图形。同时<canvas>元素的Web…...

PMP认证考试证书领取的通知
各位考生: 2022年6月、7月、8月PMI认证考试证书领取工作已经开始,您可通过以下两种方式领取证书: 1.联系本人所在培训机构,通过培训机构向考点统一代领。 2.在2023年10月20日-10月31日内,登录本网站报名系统个人账户…...
华为云HECS云服务器docker环境下安装nacos
华为云HECS云服务器,安装docker环境,查看如下文章。 华为云HECS安装docker-CSDN博客 一、拉取镜像 docker pull nacos/nacos-server二、宿主机创建挂载目录 执行如下命令: mkdir -p /usr/local/nacos/logs mkdir -p /usr/local/nacos/con…...

Oracle数据库修改序列,Oracle中的主键值和序列中的值对应不上时的处理方式
select max(stu.id) maxid from student stu; //查询student表中id的最大值select XXX_SEQ.nextval from dual; //查询student表中id对应序列XXX_SEQ的下一个值alter sequence XXX_SEQ increment by 1000; //将序列XXX_SEQ步长改为1000,对应 student表中id的最大值s…...
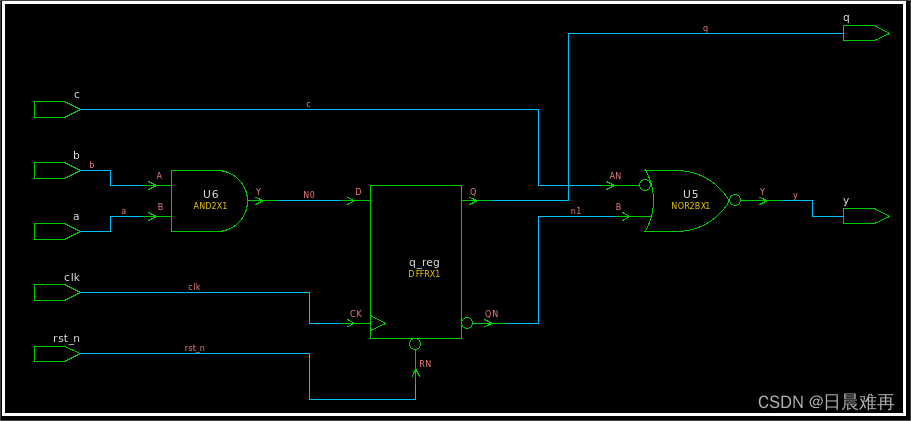
Verilog基础:避免混合使用阻塞和非阻塞赋值
相关阅读 Verilog基础https://blog.csdn.net/weixin_45791458/category_12263729.html?spm1001.2014.3001.5482 “避免在一个always块中混杂阻塞赋值和非阻塞赋值”,这条原则是著名的Verilog专家Cliff Cummings在论文SUNG2000中提出的,这个观点在公众讨…...
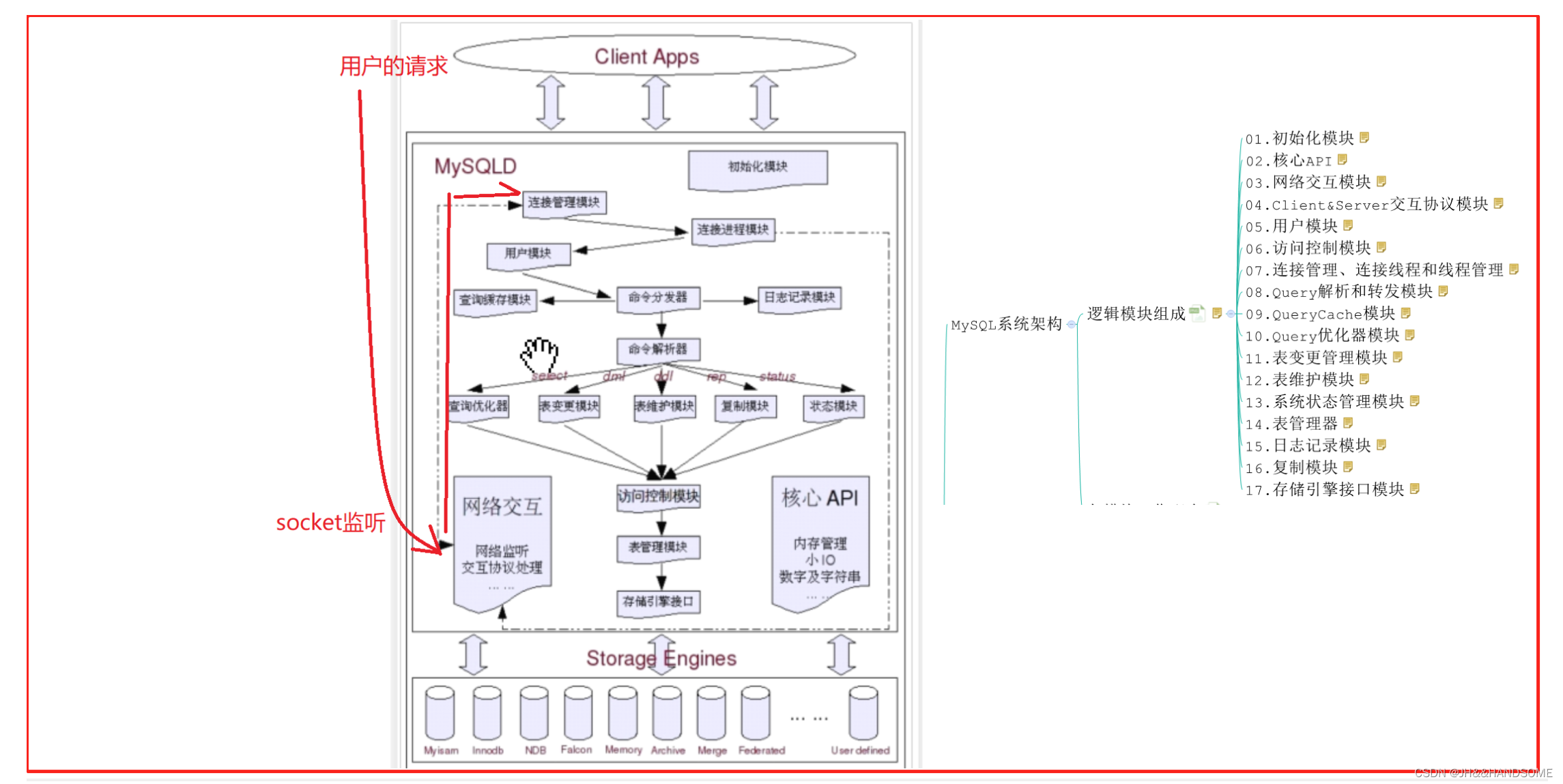
04、MySQL-------MyCat实现分库分表
目录 九、MyCat实现分库分表1、分库分表介绍:横向(水平)拆分**垂直分表**:水平分表:**分库分表** 纵向(垂直)拆分分表字段选择 2、分库分表操作:1、分析图:2、克隆主从3、…...

开源软件-禅道Zentao
禅道Zentao 简介漏洞复现SQL注入漏洞**16.5****router.class.php SQL注入** **v18.0-v18.3****后台命令执行** 远程命令执行漏洞(RCE)后台命令执行 简介 是一款开源的项目管理软件,旨在帮助团队组织和管理他们的项目。Zentao提供了丰富的功能…...

Linux生产者消费者模型
生产者消费者模型 生产者消费者模型生产者消费者模型的概念生产者消费者模型的特点生产者消费者模型优点 基于BlockingQueue的生产者消费者模型基于阻塞队列的生产者消费者模型模拟实现基于阻塞队列的生产消费模型 生产者消费者模型 生产者消费者模型的概念 生产者消费者模式就…...
【Qt-20】Qt信号与槽
一、什么是信号和槽 信号是特定情况下被发射的事件,发射信号使用emit关键字,定义信号使用signals关键字,在signals前面不能使用public、private、protected等限定符,信号只用声明,不需也不能对其进行定义实现。另外&am…...
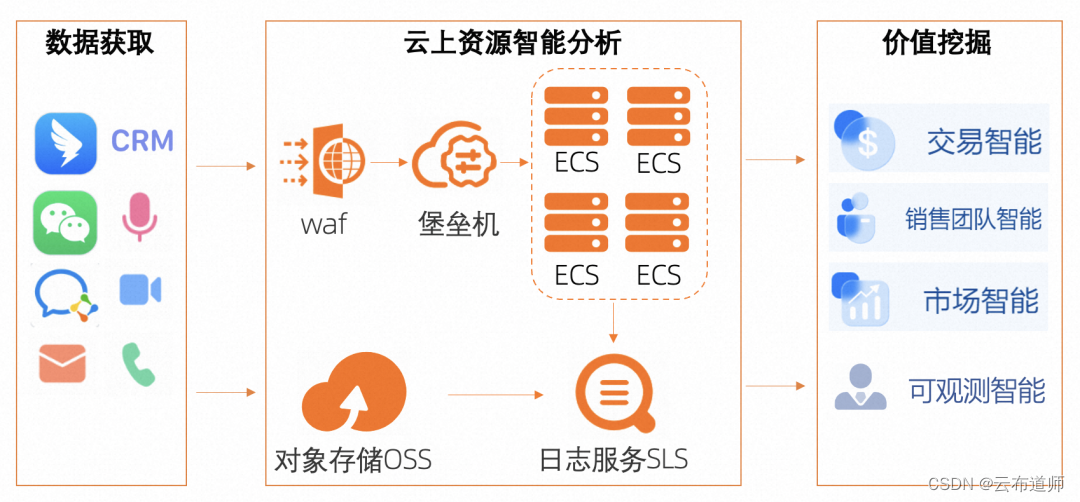
“智能+”时代,深维智信如何借助阿里云打造AI内容生成系统
云布道师 前言: 随着数字经济的发展,线上数字化远程销售模式越来越成为一种主流,销售流程也演变为线上视频会议、线下拜访等多种方式的结合。根据 Gartner 报告,到 2025 年 60% 的 B2B 销售组织将从基于经验和直觉的销售转变为数…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
