[题] 筛质数 #质数(素数)
题目
AcWing 868. 筛质数
题解
方法一:朴素筛法 及其优化:埃氏筛
从2~n枚举 i,再从小到大枚举所有已知的质数 primes[j],筛掉合数 i*primes[j],遇到新的质数就入队==
枚举所有小于n的数i,将i的所有倍数筛掉。
筛完后剩下的数就是质数。
朴素做法
void get_primes(int n ){for(int i = 2; i <= n; i ++){if(!st[i])primes[cnt ++] = i;//如果是质数,入队for(int j = i + i; j <= n; j +=i)st[j] = 1;//删掉它的所有倍数}
}
时间分析:n/2 + n/3 +....+n/n = n log n(大概)
- 朴素做法的优化:埃氏筛法。(此算法由一个埃及人发明,所以叫 埃氏筛法)
原理:当i不是质数时,没必要筛掉它的倍数,因为它的吧倍数将会是其它质数的倍数。- 筛到N时,如果N没有被筛掉,就说在
2~i-1中没有N的约数,所以N是质数。
时间是O(n log n)约等于O(n)(和O(n)一个级别)
3.补充:质数定理:1~n当中有 n / logn 个质数
埃氏筛法
void get_primes(int n ){for(int i = 2; i <= n; i ++){if(!st[i]) {primes[cnt ++] = n;//没被筛掉,说明是质数for(int j = i + i; j <= n; j += i)//干掉它的所有倍数st[j] = 1;} }
}
时间是O(n log log n)和O(n)一个级别
方法二:线性筛法求质数
原理 :n只会被n的最小质因子筛掉
操作 :
枚举i:(2~n)
i % primes[j] == 0
=>primes[j]一定是i的最小质因子.
=>primes[j]一定是primes[j] * i的最小质因子.i % primes[j] != 0
由于是从小到大枚举的质数,若此时还没枚举到i的任何一个质因子。
说明primes[j]一定小于i的最小质因子。
那么primes[j]也一定是primes[j] * i的最小质因子。
这个操作可以保证枚举到i时,所有小于等于i的合数都一定会被筛掉。
证明:对于任意一个合数x,假设primes[j]是x的最小质因数,i一定会在x之前枚举到x/primes[j],这时x就会被筛掉。
举例:
比如n=12时,x的最小质因数primes[j] = 2,
那么i一定会在12之前枚举到n/primes[j] = 6,此时就会把2*6 = 12 = n筛掉。
时间:数据范围在 107以上的时候,线性筛法比埃氏筛法快一倍。
void get_primes(int n ){for(int i = 2; i <= n; i ++){//没被筛掉说明是质数,将这个新的质数加入primes里if(!st[i]) primes[cnt ++] = i;//从小到大枚举所有已知的质数 primes[j]for(int j = 0; primes[j] <= n / i; j ++){ //当质数大于n / i的时候break;//等价于 primes[j] * i <= n;也就是筛掉所有小于n的合数就可以了//筛掉合数 i*primes[j]st[primes[j] * i] = 1; //当这句话发生的时候,primes[j]一定是i的最小质因子//那么用i的最小质因子筛掉i的目的已经达成了,所以跳出循环.if(i % primes[j] == 0) break;}}
}
代码
#include<bits/stdc++.h>
using namespace std;const int N = 1000010;int primes[N], cnt;
bool st[N];void get_primes(int n ){for(int i = 2; i <= n; i ++){if(!st[i]) primes[cnt ++] = i;for(int j = 0; primes[j] <= n / i; j ++){st[primes[j] * i] = 1;if(i % primes[j] == 0) break;}}
}int main(){int n;cin >> n;get_primes(n);cout << cnt << endl;return 0;
}
相关文章:
)
[题] 筛质数 #质数(素数)
题目 AcWing 868. 筛质数 题解 方法一:朴素筛法 及其优化:埃氏筛 从2~n枚举 i,再从小到大枚举所有已知的质数 primes[j],筛掉合数 i*primes[j],遇到新的质数就入队 枚举所有小于n的数i,将i的所有倍数筛掉。 筛完后剩下的数就是质数。 朴素做法 void ge…...
C进阶-语言文件操作
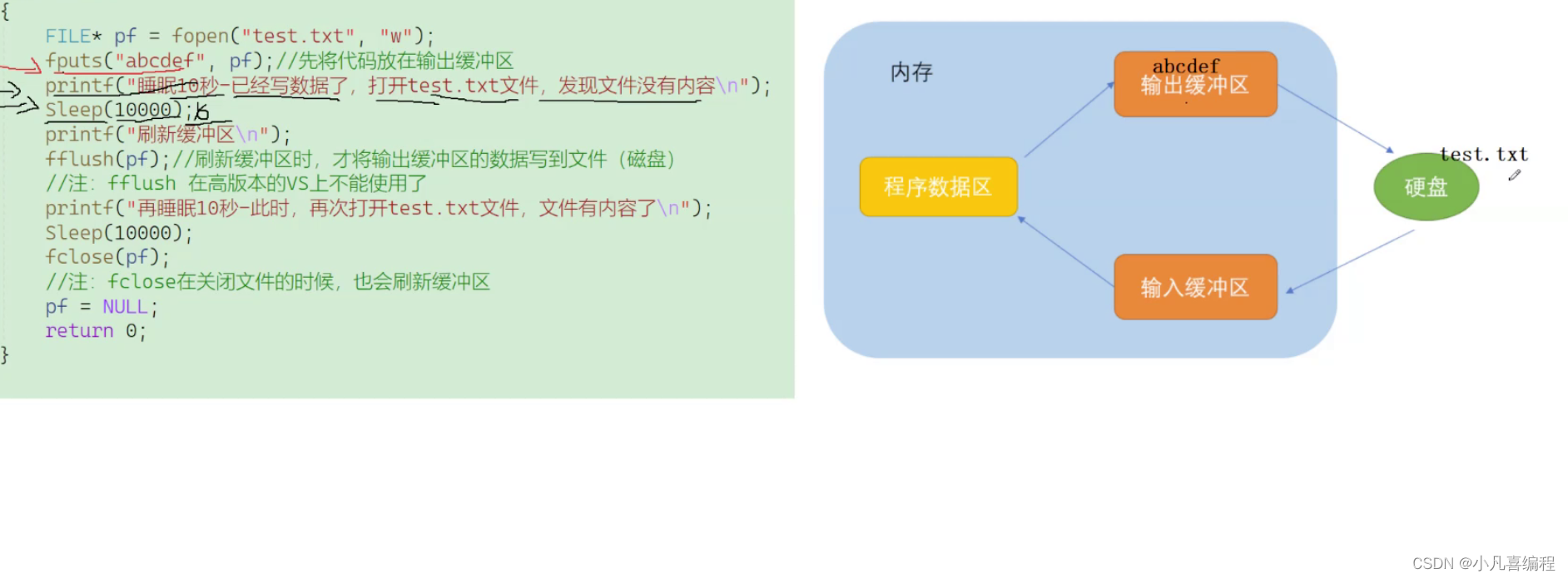
本章重点: 什么是文件 文件名 文件类型 文件缓冲区 文件指针 文件的打开和关闭文件的顺序读写文件的随机读写文件结束的判定 1. 什么是文件 磁盘上的文件是文件。 但是在程序设计中,我们一般谈的文件有两种:程序文件、数据文件 1.1 程序文件…...

17-spring aop调用过程概述
文章目录 1.源码2. debug过程1.源码 public class TestAop {public static void main(String[] args) throws Exception {saveGeneratedCGlibProxyFiles(System.getProperty("user.dir") + "/proxy");ApplicationContext ac = new ClassPathXmlApplicatio…...

微信小程序------框架
目录 视图层 WXML 数据绑定 列表渲染 条件渲染 模板 wsx事件 逻辑层 生命周期 跳转 视图层 WXML WXML(WeiXin Markup Language)是框架设计的一套标签语言,结合基础组件、事件系统,可以构建出页面的结构。 先在我们的项目中…...
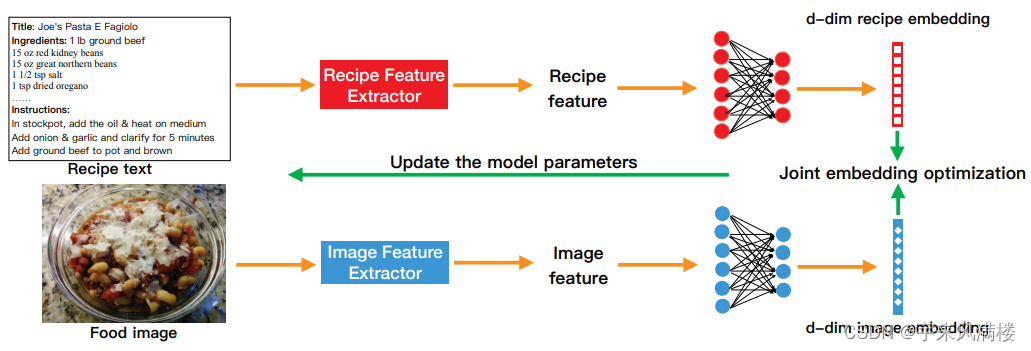
Cross-Modal Joint Embedding with Diverse Semantics
计算两个嵌入之间的相似度得分,然后利用损失函数进行联合嵌入损失最小化优化并更新参数 辅助信息 作者未提供代码...

工具 | macOS 最简方式安装 adb 工具 | Mac
工具 | macOS 最简方式安装 adb 工具 | Mac 介绍 ADB(Android Debug Bridge)是 Android开发工具包(SDK)中的一项实用工具,用于与 Android 设备进行通信和调试。 在 macOS 操作系统上安装 ADB 环境可以帮助开发人员与…...

linux进阶(脚本编程/软件安装/进程进阶/系统相关)
一般市第二种,以bash进程执行 shelle脚本编程 env环境变量 set查看所有变量 read设置变量值 echo用于控制台输出 类似java中的sout declear/typeset声明类型 范例 test用于测试表达式 if/else case while for 函数 脚本示例 软件安装及进阶 fork函数(复制一个进程(开启一个进…...

谷歌云:下一代开发者和企业解决方案的强力竞争者
自从2018年Oracle前研发总裁Thomas Kurian加入谷歌云(Google Cloud)并出任谷歌云CEO以来,业界对于谷歌云的发展就十分好奇。而谷歌云的前任CEO Diane Greene曾是VMware的创始人之一,那么两任企业级技术和解决方案出身的CEO&#x…...
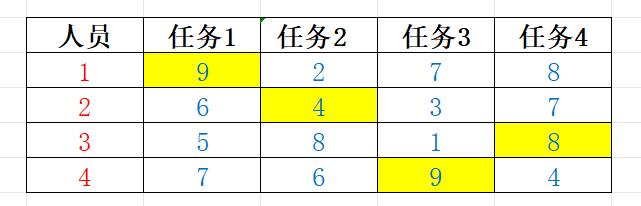
任务分配问题(回溯法)
算法设计 问题描述 有n(n≥1)个任务需要分配给n个人执行,每个任务只能分配给一个人,每个人只能执行一个任务。 第i个人执行第j个任务的成本是c[i][j](1≤i,j≤n)。求出总成本最小的分配方案 …...
【java】A卷+B卷)
华为OD 字符串消除(100分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...
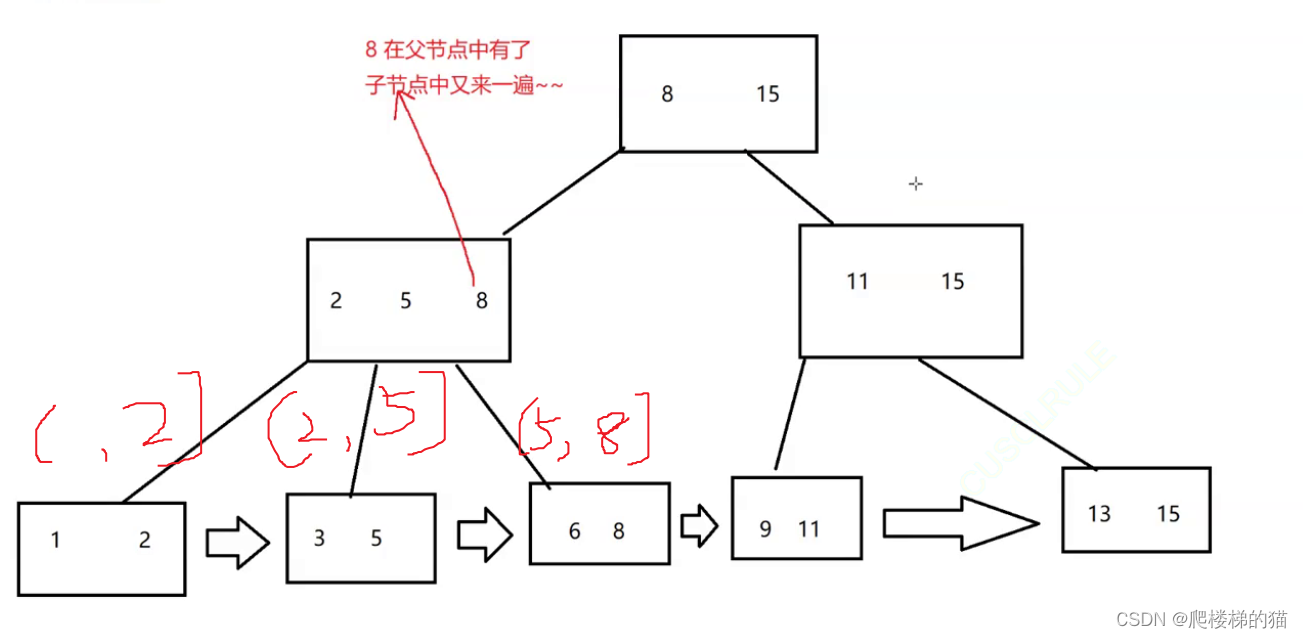
索引背后的数据结构——B+树
为什么要使用B树? 可以进行数据查询的数据结构有二叉搜索树、哈希表等。对于前者来说,树的高度越高,进行查询比较的时候访问磁盘的次数就越多。而后者只有在数据等于key值的时候才能进行查询,不能进行模糊匹配。所以出现了B树来解…...

面试用-常用注解
Configuration 注意由ConfigurationClassPostProcessor来处理ConfigurationClassPostProcessor执行这个后置处理 ConfigurationClassParser.parse执行这个方法里面会解析很多注解。1、Component 对于Component也是一样递归调用parse方法,一层层解析…...

【c++】跟webrtc学std array 4: H264PacketBuffer 包缓存
H264PacketBuffer m98代码:H264PacketBuffer 类似于PacketBuffer ,但仅用于H264// The H264PacketBuffer does the same job as the PacketBuffer but for H264 // only. To make it fit in with surronding code the PacketBuffer input/output // classes are used. 因此,…...

Nodejs Web数据库应用演示实例
Nodejs Web应用基础演示实例 Web数据库应用 一、服务器端 var express require(express); var app express(); var mysql require(mysql);//设置静态资源目录public app.use(express.static(__dirname /public));//创建mysql数据库访问连接(数据库主机地址&a…...

Vue 中setup的特性
特性四:父传子组件传参【defineProps】: 父组件(传递数据):利用自定义属性传递数据。 <template><h3>我是父组件</h3><hr /><Child :name"info.name" :age"info.age"…...

Peter算法小课堂—正整数拆分
大家可能会想:正整数拆分谁不会啊,2年级就会了,为啥要学啊 例题 正整数拆分有好几种,这里我们列举两种讲。 关系 我们看着第一幅图,头向左转90,记住你看到的图,再来看第二幅图,你…...

EDUSRC--简单打穿某985之旅
免责声明: 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直…...

vue2升级到vue2.7
vue2升级到vue2.7 小小的改进,大大的提升 只需要简单修改,开发体验得到大大提升. 为什么要升级Vue2.7 不能拒绝的理由: 组合式 API(解决mixins问题:命名冲突,隐式依赖)单文件组件内的 <script setup>语法模板表达式中支持 ESNext 语法(可选链:?.、空值合并:??)单文…...

【django2.0之Rest_Framework框架一】rest_framework序列器介绍
Django RestFramework(简称DRF) 提供了序列化器Serialzier的定义,可以帮助我们简化序列化与反序列化的过程,不仅如此,还提供丰富的类视图、扩展类、视图集来简化视图的编写工作。REST framework还提供了认证、权限、限流、过滤、分页、接口文…...
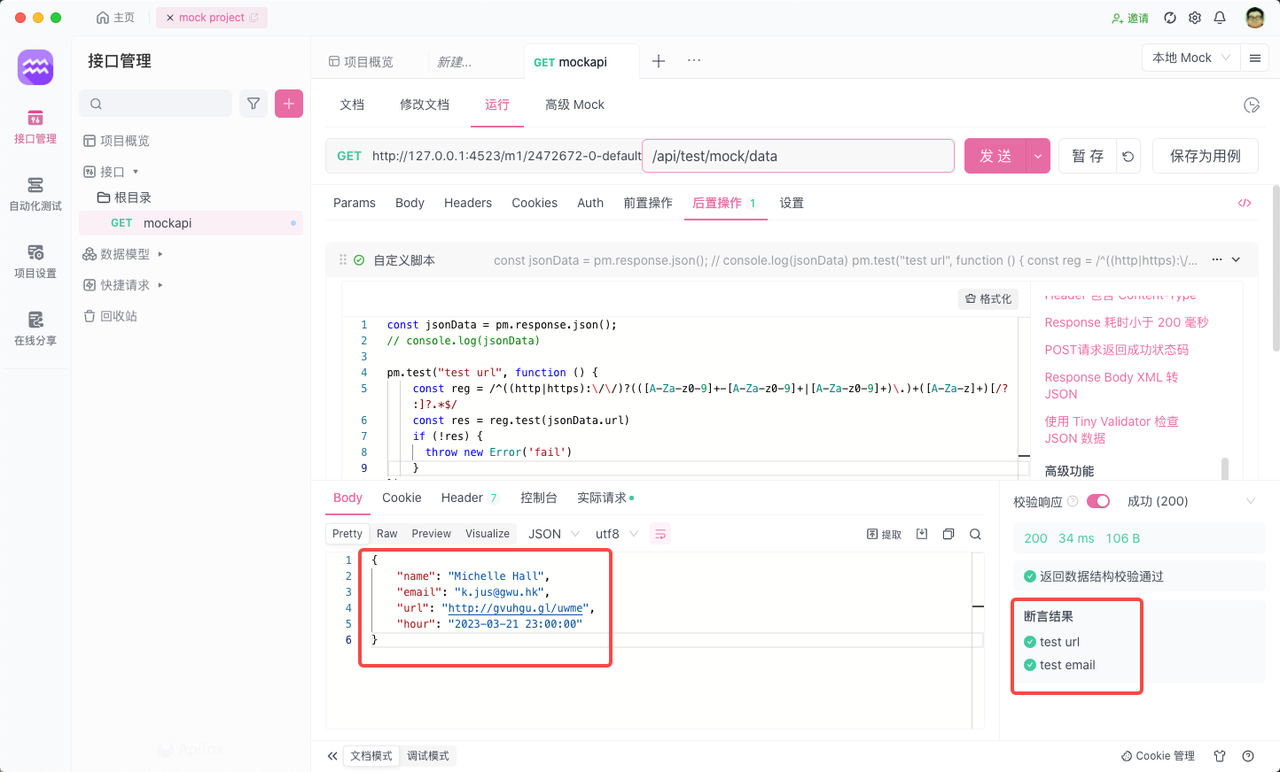
Mock 测试详解:什么是 Mock 测试
Mock测试 什么是 Mock ? Mock 的意思就是,当你很难拿到源数据时,你可以使用某些手段,去获取到跟源数据相似的假数据,拿着这些假数据,前端可以先行开发,而不需要等待后端给了数据后再开发。 Mo…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
