代碼隨想錄算法訓練營|第四十四天|01背包问题 二维、01背包问题 一维、416. 分割等和子集。刷题心得(c++)
目录
01背包問題 - DP二維數組
01 背包問題描述
暴力解
動態規劃
確認DP數組以及下標的含意
確定遞推公式
01背包问题 一维
一维DP 数組(滾動数組)
動態規劃五部曲
定義DP数組以及其下標含意
遞推公式
初始化
遍歷順序
讀題
416. 分割等和子集
自己看到题目的第一想法
看完代码随想录之后的想法
416. 分割等和子集- 實作
思路
Code
總結
自己实现过程中遇到哪些困难
今日收获,记录一下自己的学习时长
相關資料
01背包問題 - DP二維數組
01 背包問題描述
背包最高可承重重量為j,有i件物品,每件物品的重量為weight[i],並且對應的價值為value[i],每件物品只能用一次
背包放入那些物品可以達到最高的價值
01 的含意,就是每件物品只能用一次,取(1)或不取(0)
暴力解
01背包問題可以使用暴力解來解出來,就是去窮舉每一個東西取或不取最後找出最大的價值和
可以使用回溯算法去做,但時間複雜度會是 $O(2^n)$
動態規劃
確認DP數組以及下標的含意
dp[i][j]: [0, i]物品任意取,可放進容量為j的背包的最大價值。
確定遞推公式
在描述中物品有兩種狀態,一個是不放入背包,一個是放入背包
- 物品i 不放入背包: 代表我們要知道的是當下的i不放入背包j的最大價值是多少,那就是dp[i - 1][j],背包容量為j,在不放入i之前最大的是i - 1,所以得出dp[i - 1][j]
- 物品i放入背包: 代表我們要知道當下物品i放入背包之後,剩餘的背包重量可得到最大的價值是多少: dp[i - 1][j - weight[i]],這代表的是,背包可承重的重量為j 減去目前i的重量weight[i]並且不包含當前i的重量,最後再加入value[i] 代表當前的價值加上扣除當前重量的背包所能得到的最大價值。最後整合為dp[i - 1][j - weight[i]] + value[i]
那我們是要取最大的數值,所以遞推公式會變成 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i] + value[i]);
01背包问题 一维
一维DP 数組(滾動数組)
藉由壓縮dp[i - 1] 到dp[i] 因為在二維的DP遞推方程裡是dp[i][j] = max( dp[i - 1][j], dp[i - 1][j - weight[i] + value[i])
假設壓縮成一维數組,可以看成假設dp[j]跟dp[j - weight[i]] + value[i] 不用將上一層拷貝而是透過不斷更新dp[j] 來比較值。
其狀態就像是滾動著更新我們的dp数組值,透過維護dp[j]的遍歷順序來維護裡面的值與dp二維数組一致
動態規劃五部曲
定義DP数組以及其下標含意
dp[j]: 背包重量為j的最大價值為dp[j]
遞推公式
與二维數組一樣,dp[j]的數值可以透過當前dpj 以及dp[j - weighti 兩者做比較。
所以遞推公式可以將i去除掉變成
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
初始化
dp数組在dp[0]時,根據定義,需要將dp[0]初始化為0,並且根據遞推公式,每次都會取最大值,所以其他数值也應該初始化為dp数組中最小的值,也就是0
所以在初始化時,將dp数組全部初始化為0
遍歷順序
在二维數組中,每一層的數值都是當前位置的正上方以及左上方的數據得出
從二维壓縮成一维數組,我們需要模擬二维數組的方式
所以根據我們的遞推公式,我們不能使用正序遍歷,不然原本在二维數組中左上方的數據就會被覆蓋掉
而使用倒序可以保證每一層的數據都是由二维數組上一層正上方以及左上方得出的。
透過倒敘更新,確保了在考慮當前物品時,dp[j - weight[i]]仍然代表前一個物品的狀態,但是如果使用正序,那dp[j - weight[i]]就會被提早更新了
如下
假設我們有以下物品和背包:
物品重量: w = [2,3] 物品價值: v = [3,4] 背包最大容量: W = 5
-
使用一維數組正序更新時:
物品\\背包 | 0 | 1 | 2 | 3 | 4 | 5 | 進行的操作 ----------------------------------- ------------ | 0 | 0 | 0 | 0 | 0 | 0 | 初始化2 | 0 | 0 | 3 | 3 | 3 | 3 | 考慮物品1 (w=2, v=3)3 | 0 | 0 | 3 | 4 | 7 | 7 | 考慮物品2 (w=3, v=4)當我們考慮物品2時,對於背包容量4,dp[4]是基於dp[1](已被更新的)和dp[4-w[2]=1]計算
-
使用一維數組倒序更新時
物品\\背包 | 0 | 1 | 2 | 3 | 4 | 5 | 進行的操作 ----------------------------------- ------------ | 0 | 0 | 0 | 0 | 0 | 0 | 初始化2 | 0 | 0 | 3 | 3 | 3 | 3 | 考慮物品1 (w=2, v=3)3 | 0 | 0 | 3 | 4 | 5 | 7 | 考慮物品2 (w=3, v=4)當我們考慮物品2和背包容量4時,dp[4]是基於dp[1](尚未更新的)和dp[4-w[2]=1]計算的
在影片講解的部分,有個彈幕寫了以下這段,分享給你
一维数组就像走楼梯,你去二楼,就必须从一楼上,去三楼也要从一楼走;倒叙就还好比下楼,想去几楼都不用重复路过其他楼层。
並且需要先遍歷物品在遍歷背包,因為需要上一個物品的值,如果先遍歷背包,則只抓到一個物品的值。
讀題
416. 分割等和子集
自己看到题目的第一想法
看完跟01背包問題沒有辦法有很直接的連結,我大致有想到一個是dp[i][j]代表的是[0 ~ i][j ~ size()]的區間是否相等,但感覺有些地方沒有想清楚,先看題解。
看完代码随想录之后的想法
想法很巧妙如果有一個背包等於所有和的一半,剩下的元素相加也等於剩餘的一半 dp[j]: 容量為j的背包,最大價值為dp[j],並且數組中的重量跟價值可以看成是一致的
並判斷dp[target] == target。dp数組初始化為0 ,並且背包重量設為target + 1
忘記思考到target如果不能被2整除,那就是要return false。
416. 分割等和子集- 實作
思路
-
定義DP數組以及下標的含意
target: 假設子序和的重量為總和的一半,那代表另一半為剩餘的一半。
假設總和除2餘1代表不會有一個子序和等於另一個子序和
dp[j] : 背包重量 j 的最大價值為dp[j]
nums数組中,重量與價值就是nums[i]
-
遞推公式
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
-
根據遞推公式,確定DP數組如何初始化
dp[0]要初始化為0,其他部分也要更新為正整數下的最小位数0
-
確定遍歷順序
避免覆蓋掉上一次的值,所以要使用倒敘遍歷
-
打印dp數組 (debug);
Code
class Solution {
public:bool canPartition(vector<int>& nums) {int target = 0;for(int i = 0; i < nums.size(); i++) {target += nums[i];}if (target % 2 == 1) return false;target /= 2;vector<int> dp(target + 1, 0);for(int i = 0; i < nums.size(); i++) {for(int j = target; j >= nums[i]; j--) {dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}if(dp[target] == target) return true;}return false;}
};
總結
自己实现过程中遇到哪些困难
困難點主要是在思考二维數組壓縮成一维數組的部分,這個部分思考比較久,並且在416分割等和子集中,也是遇到了點問題,在思考上沒有想到nums[i]是重量與價值相等,彈點通之後就比較理解了
今日收获,记录一下自己的学习时长
今天大概學了3hr,主要是在理解01背包的思維與想法。
相關資料
● 今日学习的文章链接和视频链接
算法圖解
01背包问题 二维
https://programmercarl.com/背包理论基础01背包-1.html
视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili
01背包问题 一维
https://programmercarl.com/背包理论基础01背包-2.html
视频讲解:带你学透01背包问题(滚动数组篇) | 从此对背包问题不再迷茫!_哔哩哔哩_bilibili
416. 分割等和子集
本题是 01背包的应用类题目
https://programmercarl.com/0416.分割等和子集.html
视频讲解:动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集_哔哩哔哩_bilibili
相关文章:
)
代碼隨想錄算法訓練營|第四十四天|01背包问题 二维、01背包问题 一维、416. 分割等和子集。刷题心得(c++)
目录 01背包問題 - DP二維數組 01 背包問題描述 暴力解 動態規劃 確認DP數組以及下標的含意 確定遞推公式 01背包问题 一维 一维DP 数組(滾動数組) 動態規劃五部曲 定義DP数組以及其下標含意 遞推公式 初始化 遍歷順序 讀題 416. 分割等和子集 自己看到题目的第…...
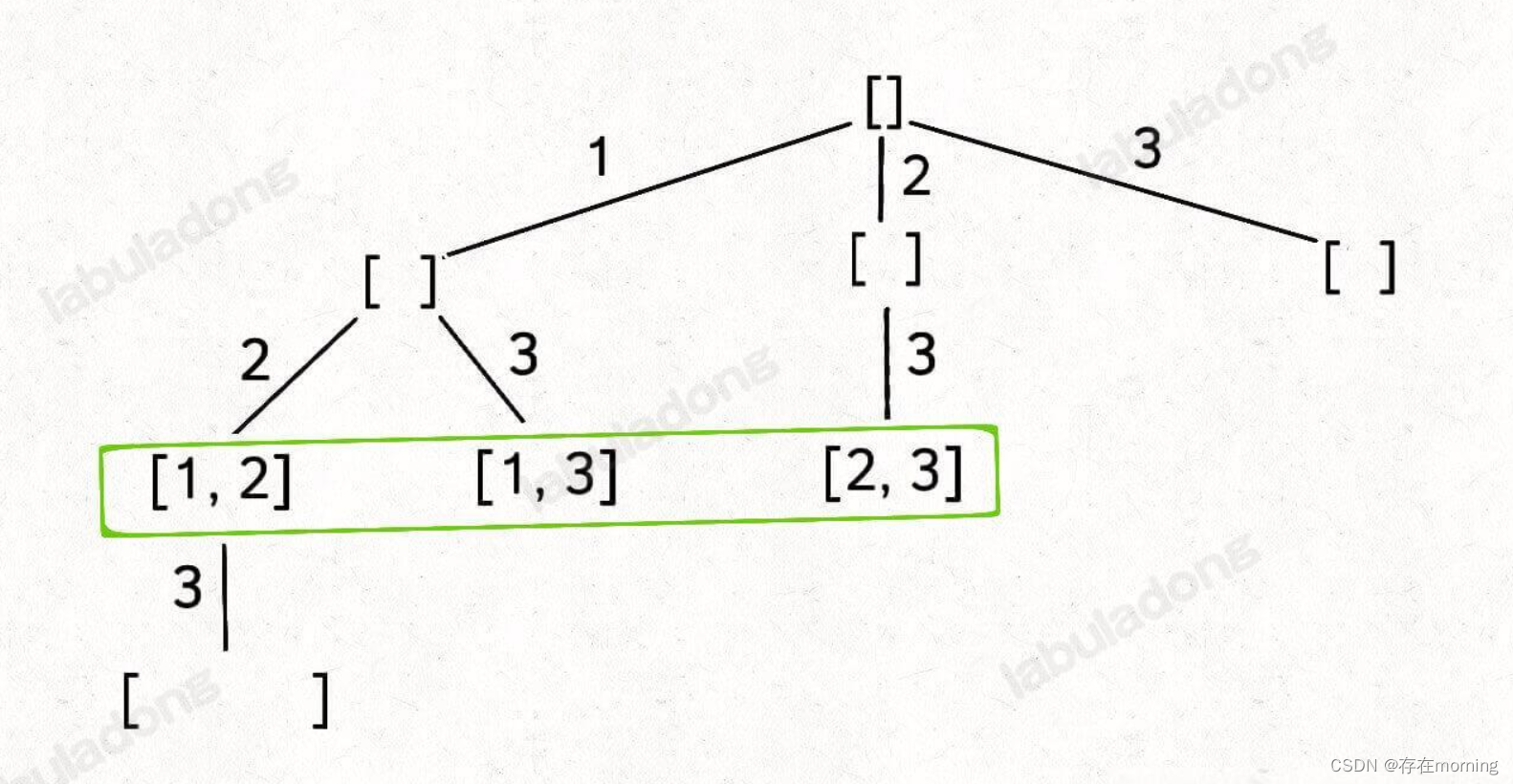
【算法训练-回溯算法 零】回溯算法解题框架
抽象地说,解决一个回溯问题,实际上就是遍历一棵决策树的过程,树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍,把叶子节点上的答案都收集起来,就能得到所有的合法答案。站在回溯树的一个节点上,你…...

GAN.py
原代码地址:github.com/zqhang/MTGFLOW 目录 def ConvEncoder() def ConvDecoder() class CNNAE(torch.nn.Module): class R_Net(torch.nn.Module): class D_Net(torch.nn.Module): def R_Loss() def D_Loss()…...
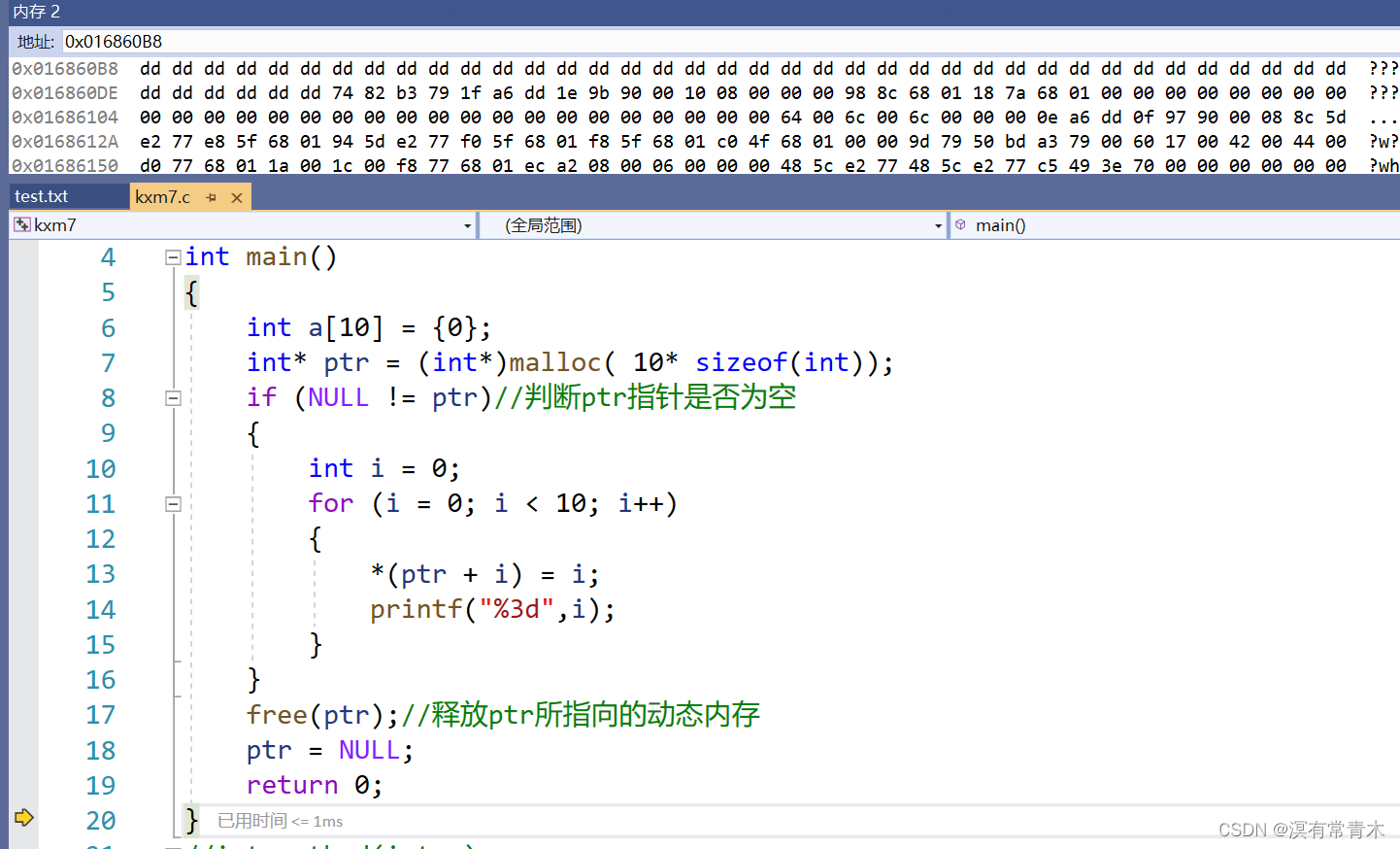
C语言动态内存管理
1.为什么要动态内存分配? int val 20; int a[10]{0};上面我们声明并定义了一个大小为4字节的整型变量,一个容量为10*4字节的整型数组。 开辟方式:我们在栈上开辟。 开辟空间的方式有两个特点: 1. 空间开辟 大小是固定 的。 2. 数组在申明…...
)
小红书商品详情API接口(商品详情页面数据接口)
小红书商品详情API接口(商品详情页面数据接口 小红书商品详情API接口(商品详情页面数据接口)代码对接如下: 1.公共参数 名称类型必须描述keystring是get请求方式拼接在url中,点击获取api_namestring是 api接口名称cachestrin…...

nginx配置文件的内容解释和简化方案
文章目录 配置文件内容理解配置文件精简nginx.confapp1.conf 配置文件内容理解 events {worker_connections 1024; }http {include mime.types;default_type application/octet-stream;sendfile on;keepalive_timeout 65;client_max_body_size 50m;client…...
)
Java设计模式之访问者模式(Visitor Pattern)
访问者模式(Visitor Pattern)是一种行为型设计模式,它允许在不修改现有对象结构的情况下定义新的操作。该模式将操作封装在一个访问者对象中,使得可以在不改变被访问对象的类的前提下,通过访问者对象对被访问对象进行新…...
others-AppLovin广告接入
title: others-AppLovin广告接入 categories: Others tags: [广告, AppLovin] date: 2023-10-20 10:07:01 comments: false mathjax: true toc: true others-AppLovin广告接入 前篇 官方 - https://www.applovin.com/ Android sdk - https://github.com/AppLovin/AppLovin-MAX…...
ESP32集成开发环境Espressif-IDE安装 – Windows
陈拓 2023/10/15-2023/10/16 1. 概述 Espressif IDE是一个基于Eclipse CDT的集成开发环境(IDE),用于使用ESP-IDF框架开发物联网应用程序。这是一个专门为ESP-IDF构建的独立定制IDE。Espressif IDE附带了IDF Eclipse插件、重要的Eclipse CDT插…...

python之if else语句介绍
python之if else语句介绍 在Python中,if和else是两种重要的控制流语句,它们用于根据特定的条件来执行不同的代码块。以下是它们的用法和详细介绍: 1)if语句 if语句用于在满足某种条件时执行特定的代码块。它的基本语法如下&#…...
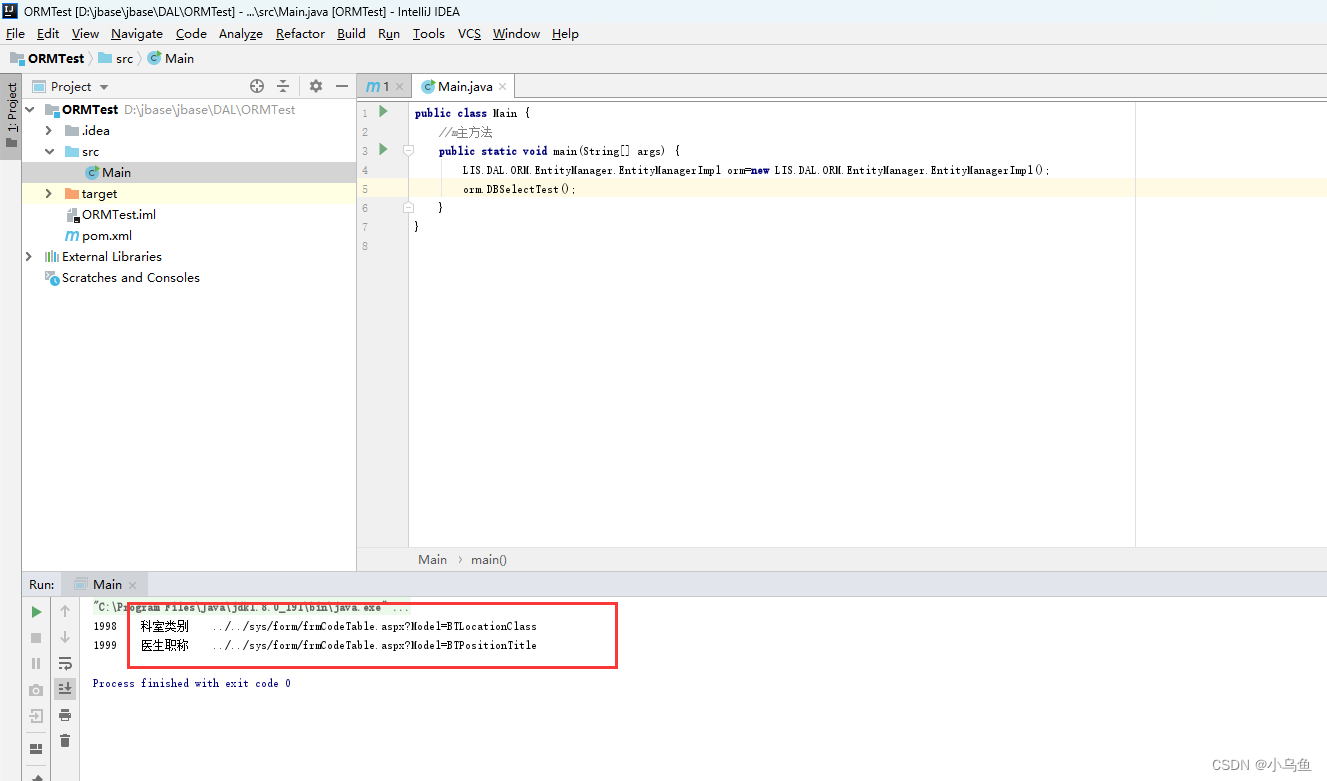
Java版ORM最初雏形
经过一个晚上的加班,终于把ORM初步结构工程搭好了。工程依赖有点难用,编辑器提示比VS差很多。 首先LIS.Core创建一个最初的容器雏形,先能反射得到对象给ORM获得数据库驱动 然后ORM创建数据库驱动差异接口,不同数据库实现接口后配…...
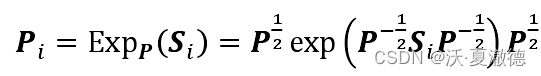
黎曼几何与切空间之间的投影
公式: 从黎曼空间投影到切空间,其中P为黎曼均值,也是切空间的参考中心点,Pi是要投影到切空间的点。 从切空间投影回来,其中Si为切空间中的向量。 function Tcov CovToTan(cov,Mcov)Cm12 Mcov^(-1/2);X_new logm(Cm…...
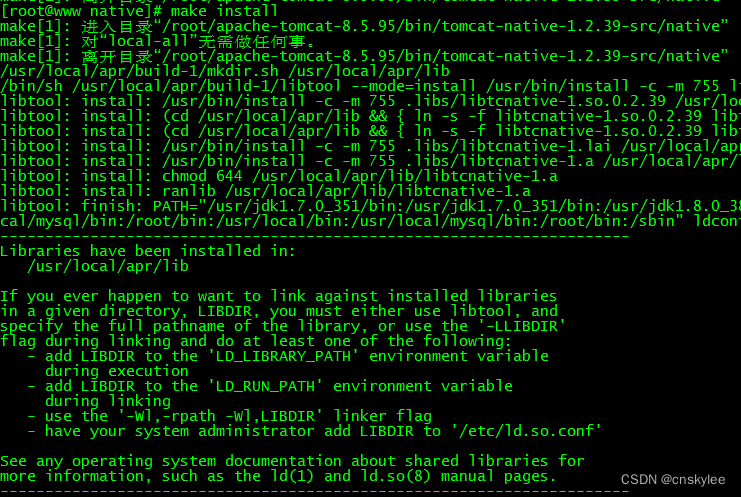
【Tomcat】为Tomcat服务配置本地Apr库以提升性能
关于 apr 和 apr-util 对 Tomcat 服务的性能提升的说明: 要测APR给tomcat带来的好处最好的方法是在慢速网络上(模拟Internet),将Tomcat线程数开到300以上的水平,然后模拟一大堆并发请求。如果不配APR,基本…...

普通人在当前大环境下——少看宏观,多看具体
前言 宏观叙事,简而言之,就是从宏观把握历史社会的发展,寻找其中永恒的共性。我们大概听过此类的话:贸易战导致本地经济下滑、气候变化是因为过去几十年的工业发展、大环境不行导致不赚钱。此类叙事方式,身边人聊的甚欢,在媒体、社交圈、日常社群交流中,随处可见。以前…...

用echarts在vue2中实现3d饼图
先看效果,再看文章: 一、安装插件 3d的图不仅用到echarts,还用到了echarts-gl,因此都需要安装一下哦~ npm install echarts npm install echarts-gl2.0.9 //可以指定版本,也可不指定二、在main.js中引入 import * …...
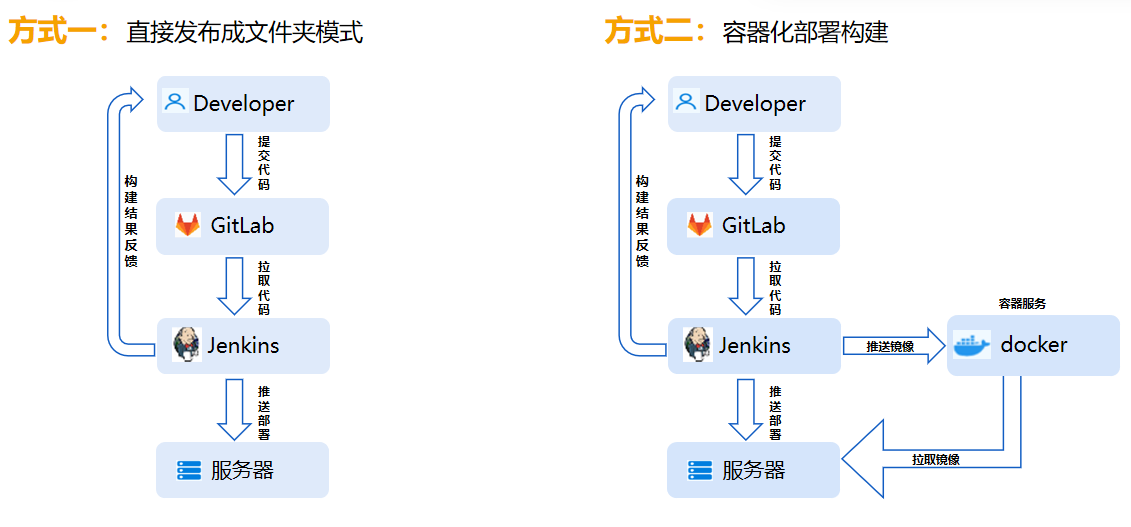
低代码助力软件开发
低代码开发工具正在日益变得强大,它正不断弥合着前后端开发之间的差距。对于后端来说,基于低代码平台开发应用时,完全不用担心前端的打包、部署等问题,也不用学习各种框架(Vue、React、Angular等等)&#x…...

C嘎嘎之类和对象上
> 作者简介:დ旧言~,目前大二,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:掌握类的引用和定义,熟悉类成员函数的…...
Vue 3使用 Iconify 作为图标库与图标离线加载的方法、 Icones 开源在线图标浏览库的使用
之前一直naive-ui搭配使用的是xicons,后来发现Iconify支持的图标合集更多,因此转而使用Iconify。 与FontAwesome不同的是,Iconify配合Icones相当于是一个合集,Iconify提供了快捷引入图标的方式,而Icones是一个大的图标…...
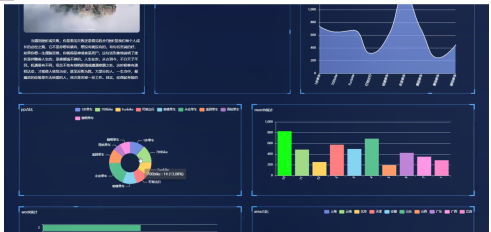
springboot+vue基于Spark的共享单车数据存储系统的设计与实现【内含源码+文档+部署教程】
博主介绍:✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立工作室。专注于计算机相关专业毕业设计项目实战6年之久,选择我们就是选择放心、选择安心毕业✌ 🍅由于篇幅限制,想要获取完整文章或者源码,或者代做&am…...

如何使双核心的ESP32开启双核功能同时执行多任务
如何使双核心的ESP32开启双核功能同时执行多任务 简介查看ESP32当前哪一个内核在执行任务双核同时执行任务总结 简介 ESP32-WROOM-32模组内置两个低功耗 Xtensa 32-bit LX6 MCU,两个 CPU 核(core 0与core 1)可以被单独控制。可以在两个内核上…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
