ccc-pytorch-感知机算法(3)
文章目录
- 单一输出感知机
- 多输出感知机
- MLP反向传播
单一输出感知机
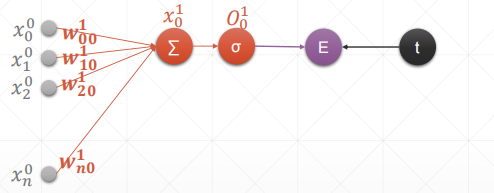
内容解释:
- w001w^1_{00}w001:输入标号1连接标号0(第一层)
- x00x_0^0x00:第0层的标号为0的值
- O11O_1^1O11:第一层的标号为0的输出值
- t:真实值
- σ\sigmaσ:激活函数
公式推导:
E=12(O01−t)\begin{aligned} E=\frac{1}{2}(O_0^1-t)^\ \end{aligned}E=21(O01−t)
添加常数便于求导,不影响单调性
∂E∂wj0=(O0−t)∂O0∂wj0=(O0−t)∂σ(x0)∂wj0=(O0−t)O0(1−O0)∂x01∂wj0注:[σ(x0)=O0]=(O0−t)O0(1−O0)xj0\begin{aligned} \frac{\partial E}{\partial w_{j0}} &=(O_0-t)\frac{\partial O_0}{\partial w_{j0}}\\ &=(O_0-t)\frac{\partial \sigma(x_0)}{\partial w_{j0}}\\ &=(O_0-t) O_0(1- O_0)\frac{\partial x_0^1}{\partial w_{j0}} 注:[\sigma(x_0)=O_0]\\ &=(O_0-t) O_0(1- O_0)x_j^0 \end{aligned}∂wj0∂E=(O0−t)∂wj0∂O0=(O0−t)∂wj0∂σ(x0)=(O0−t)O0(1−O0)∂wj0∂x01注:[σ(x0)=O0]=(O0−t)O0(1−O0)xj0
简单实践代码:
x = torch.randn(1,10)
w = torch.randn(1,10,requires_grad=True)
o = torch.sigmoid(x@w.t())
loss = F.mse_loss(torch.ones(1,1),o)
loss.shape
loss.backward()
w.grad

多输出感知机
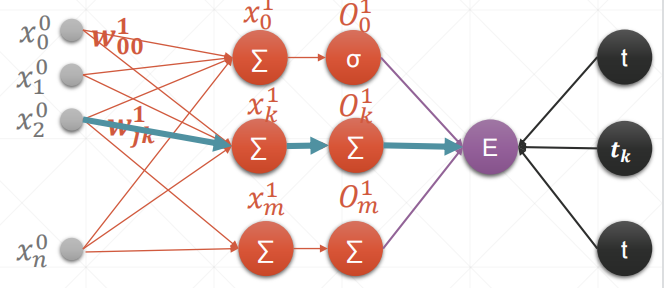
内容解释:
和单层的一摸一样,只是多了几个输出,注意下标即可
公式推导:
E=12∑(Oik−tk)\begin{aligned} E=\frac{1}{2}\sum(O_i^k-t_k)^\ \end{aligned}E=21∑(Oik−tk)
添加常数便于求导,不影响单调性
∂E∂wjk=(Ok−tk)∂Ok∂wjk注:[下标对上才有值]=(Ok−tk)∂σ(xk)∂wjk=(Ok−tk)Ok(1−Ok)∂xk1∂wjk=(Ok−tk)Ok(1−Ok)xj1\begin{aligned} \frac{\partial E}{\partial w_{jk}} &=(O_k-t_k)\frac{\partial O_k}{\partial w_{jk}}注:[下标对上才有值]\\ &=(O_k-t_k)\frac{\partial \sigma(x_k)}{\partial w_{jk}}\\ &=(O_k-t_k) O_k(1- O_k)\frac{\partial x_k^1}{\partial w_{jk}} \\ &=(O_k-t_k) O_k(1- O_k)x_j^1 \end{aligned}∂wjk∂E=(Ok−tk)∂wjk∂Ok注:[下标对上才有值]=(Ok−tk)∂wjk∂σ(xk)=(Ok−tk)Ok(1−Ok)∂wjk∂xk1=(Ok−tk)Ok(1−Ok)xj1
即只需要输出和对应输入即可计算
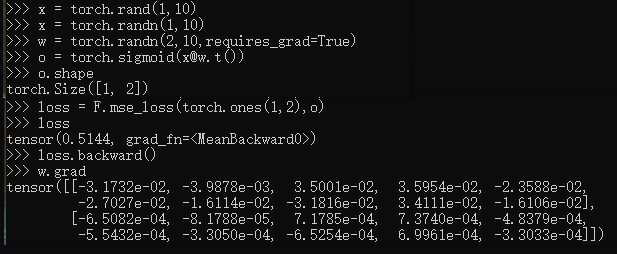
简单实践代码:
x = torch.randn(1,10)
w = torch.randn(2,10,requires_grad=True)
o = torch.sigmoid(x@w.t())
loss = F.mse_loss(torch.ones(1,2),o)
loss.shape
loss.backward()
w.grad
MLP反向传播
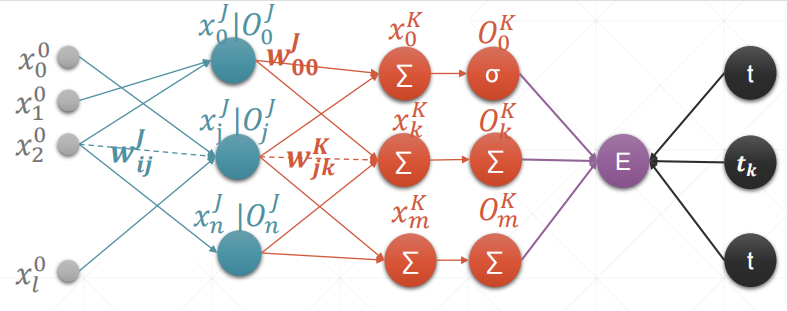
内容解释:
MLP即Multi-Layer Perceptron,多层感知机
公式推导:
∂E∂Wij=∂∂Wij12∑k∈K(Ok−tk)2=∑k∈K(Ok−tk)∂∂WijOk=∑k∈K(Ok−tk)∂∂Wijσ(xk)=∑k∈K(Ok−tk)Ok(1−Ok)∂xk∂wij=∑k∈K(Ok−tk)Ok(1−Ok)∂xk∂Oj⋅∂Oj∂wij=∑k∈K(Ok−tk)Ok(1−Ok)Wjk∂Oj∂wij=Oj(1−Oj)∂xj∂Wij∑k∈K(Ok−tk)Ok(1−Ok)Wjk=Oj(1−Oj)Oi∑k∈K(Ok−tk)Ok(1−Ok)Wjk注:[层数从左到右为i,j,k]\begin{aligned} \frac{\partial E}{\partial W_{ij}} &=\frac{\partial }{\partial W_{ij}}\frac{1}{2}\sum_{k\in K}(O_k-t_k)^2\\ &=\sum_{k\in K}(O_k-t_k)\frac{\partial }{\partial W_{ij}}O_k\\ &=\sum_{k\in K}(O_k-t_k)\frac{\partial }{\partial W_{ij}}\sigma(x_k)\\ &=\sum_{k\in K}(O_k-t_k) O_k(1- O_k)\frac{\partial x_k}{\partial w_{ij}} \\ &=\sum_{k\in K}(O_k-t_k) O_k(1- O_k)\frac{\partial x_k}{\partial O_j}\cdot\frac{\partial O_j}{\partial w_{ij}}\\ &=\sum_{k\in K}(O_k-t_k) O_k(1- O_k)W_{jk}\frac{\partial O_j}{\partial w_{ij}}\\ &=O_j(1-O_j)\frac{\partial x_j}{\partial W_{ij}}\sum_{k\in K}(O_k-t_k) O_k(1- O_k)W_{jk}\\ &=O_j(1-O_j)O_i\sum_{k\in K}(O_k-t_k) O_k(1- O_k)W_{jk}\\ &注:[层数从左到右为 i ,j,k] \end{aligned}∂Wij∂E=∂Wij∂21k∈K∑(Ok−tk)2=k∈K∑(Ok−tk)∂Wij∂Ok=k∈K∑(Ok−tk)∂Wij∂σ(xk)=k∈K∑(Ok−tk)Ok(1−Ok)∂wij∂xk=k∈K∑(Ok−tk)Ok(1−Ok)∂Oj∂xk⋅∂wij∂Oj=k∈K∑(Ok−tk)Ok(1−Ok)Wjk∂wij∂Oj=Oj(1−Oj)∂Wij∂xjk∈K∑(Ok−tk)Ok(1−Ok)Wjk=Oj(1−Oj)Oik∈K∑(Ok−tk)Ok(1−Ok)Wjk注:[层数从左到右为i,j,k]
如果将仅与第k层相关的信息作为一个函数可以写作:
∂E∂Wij=OiOj(1−Oj)∑k∈KδkWjk\begin{aligned} \frac{\partial E}{\partial W_{ij}}=O_iO_j(1-O_j)\sum_{k\in K}\delta _kW_{jk} \end{aligned}∂Wij∂E=OiOj(1−Oj)k∈K∑δkWjk
所以一个前面层的值依赖后面层的信息,需要倒着计算才行哦
相关文章:

ccc-pytorch-感知机算法(3)
文章目录单一输出感知机多输出感知机MLP反向传播单一输出感知机 内容解释: w001w^1_{00}w001:输入标号1连接标号0(第一层)x00x_0^0x00:第0层的标号为0的值O11O_1^1O11:第一层的标号为0的输出值t:真实…...

LeetCode 225.用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。实现 MyStack 类:void push(int x) 将元素 x 压入栈顶。int pop() 移除并返回栈顶元素。int top() …...

【面试】spring控制反转IOC
目录一.说明二.ioc的概念和作用三.优点四.实现机制五.IOC和DI的区别六.设计原则一.说明 1.ioc的概念2.ioc的作用3.ioc的优点4.ioc的实现机制 二.ioc的概念和作用 1.全称Inversion of Control2.控制:创建对象的控制权3.反转:以前对象是程序员主动去new…...

Spring 事务管理详解及使用
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

LeetCode 232.用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):实现 MyQueue 类:void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开头的元…...
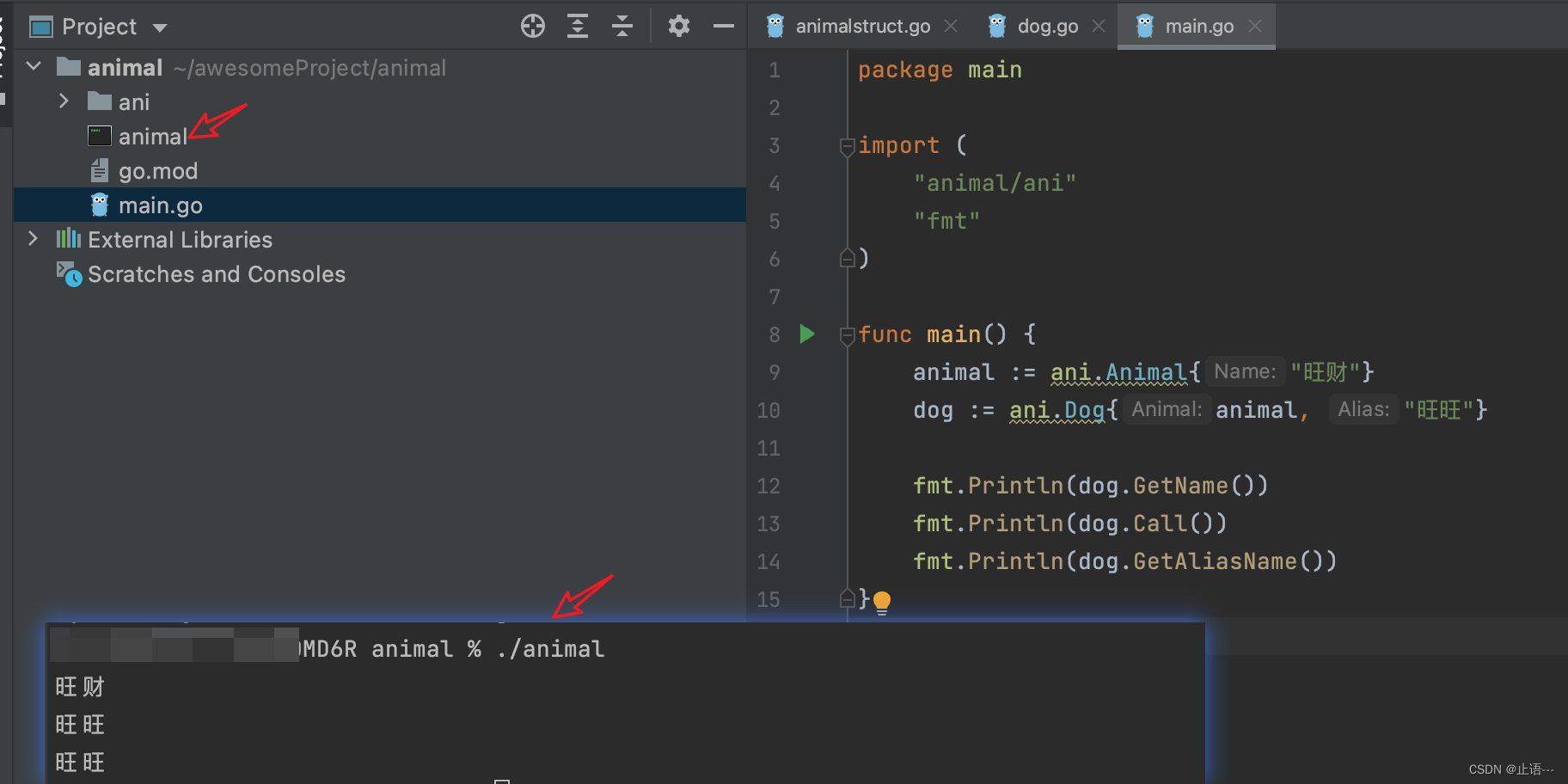
go面向对象思想封装继承多态
go貌似都没有听说过继承,当然这个继承不像c中通过class类的方式去继承,还是通过struct的方式,所以go严格来说不是面向对象编程的语言,c和java才是,不过还是可以基于自身的一些的特性实现面向对象的功能,面向…...
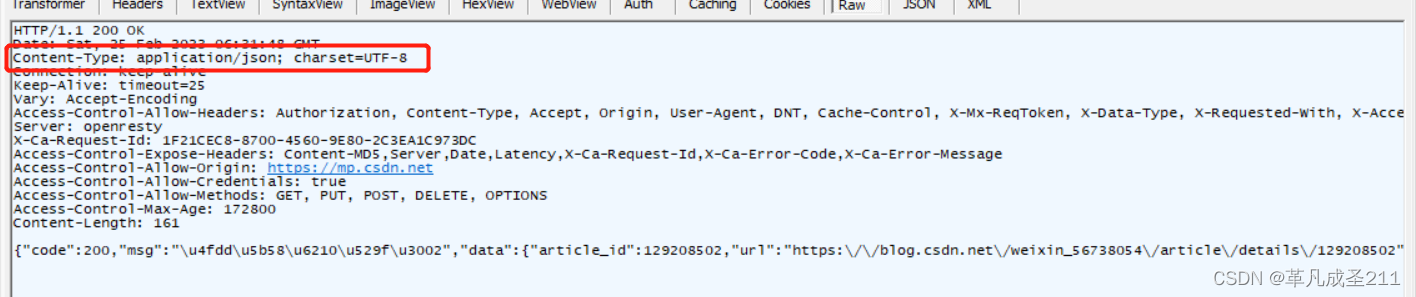
【网络原理9】HTTP响应篇
在前两篇文章当中,已经分别介绍了HTTP是什么,以及常见的请求头当中的属性。【网络原理7】认识HTTP_革凡成圣211的博客-CSDN博客HTTP抓包,Fiddler的使用https://blog.csdn.net/weixin_56738054/article/details/129148515?spm1001.2014.3001.…...

SpringCloud之Seata(二)
4.Seata如何应用于项目? 安装seata及修改配置 4.1 官网下载Seata安装包 4.2 修改seata/config.txt 4.2.1 修改存储方式 store.db.dbTypemysql store.db.driverClassNamecom.mysql.jdbc.Driver store.db.urljdbc:mysql://你的IP:3306/seata?useUnicodetrue sto…...

【Redis-入门阶段】基本数据结构
Redis支持多种数据结构,包括字符串、列表、哈希、集合和有序集合。这些数据结构在Redis中被称为键值对,其中键是一个字符串,值可以是一个字符串、列表、哈希、集合或有序集合。接下来,我们将详细介绍这些数据结构的使用方法。字符…...
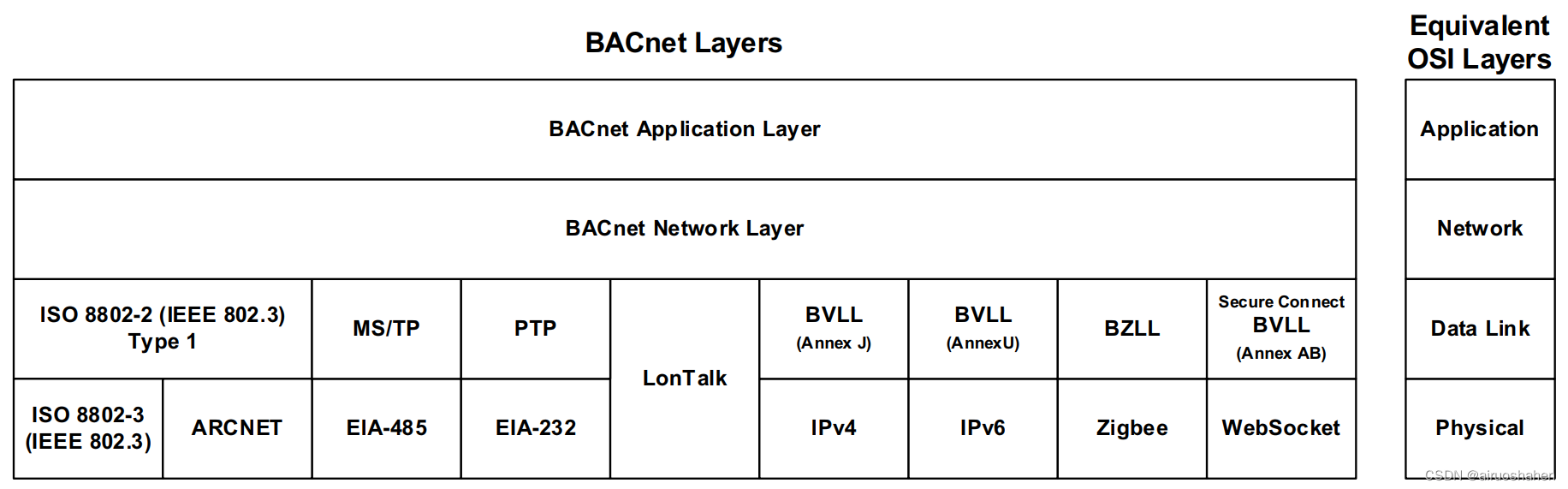
BACnet协议详解————MS/TP物理层,数据链路层和网络层
文章目录写在前面1 物理层2 数据链路层MSTP的流程如下noteMS/TP帧格式3 网络层写在前面 这周加更一篇,来弥补一下之前落下的进度。简单的说两句,之前讲应用层的时候,只是跟官方的手册来同步一下,但是从个人理解来说,自…...

Tomcat
Tomcat 1 简介 1.1 什么是Web服务器 Web服务器是一个应用程序(软件),对HTTP协议的操作进行封装,使得程序员不必直接对协议进行操作,让Web开发更加便捷。主要功能是"提供网上信息浏览服务"。 Web服务器是安…...

创客匠人直播:构建公域到私域的用户增长模型
进入知识付费直播带货时代,很多拥有知识技能经验的老师和培训机构吃到了流量红利。通过知识付费直播,老师们可以轻松实现引流、变现,还可以突破时间、地域的限制,为全国各地的学员带来优质的教学服务,因此越来越受到教…...

机试指南
文章目录零、绪论和IDE安装int取值范围常犯的编程小错误一、枚举和模拟 (暴力求解)(一) 枚举1.Reverse函数 求 反序数2.程序出错的原因1.编译错误 (compile):基本语法错误2.链接错误 (link):函数名写错了3.运行错误 (run):结果与预期不符&…...

Android CTA认证设定首选网络类型
需求 硬件只支持4G,过CTA认证时打网络电话,会出现3G网络的选择,会导致过不了,需要禁用3G网络选择功能。 Android 8.1.0 分析 可adb命令查看当前的网络类型 getprop | grep “network” 打印如下: [gsm.network.type]: [LTE,LTE] [ro.telephony.default_network]: [9] …...

Android 动态切换应用图标方案
经常听到大家讨论类似的需求,怀疑大厂是不是用了此方案,据我个人了解,多数头部 app 其实都是发版来更新节假日的 icon。当然本方案也是一种可选的方案,以前我也调研过,存在问题和作者所述差不多,此外原文链…...
SMART PLC斜坡函数功能块(梯形图代码)
斜坡函数Ramp的具体应用可以参看下面的文章链接: PID优化系列之给定值斜坡函数(PLC代码+Simulink仿真测试)_RXXW_Dor的博客-CSDN博客很多变频器里的工艺PID,都有"PID给定值变化时间"这个参数,这里的给定值变化时间我们可以利用斜坡函数实现,当然也可以利用PT1…...

不那么认真的linux复习
这是个不那么认真的linux总结,可能有一些错误 1、linuxkernel(内核)shell(外壳)fs(文件系统)pro/uti/tol(应用程序) 2、ls(列出文件) -a…...

Redis系列文章总纲
跟着老万学Redis 前言 从事开发工作这么久,很多核心技术其实都还只是局限在满足日常开发工作中的基础使用,并没有完整的总结研究。今年的目标之一是完成几个技术栈的系列博客,系统的总结一下知识体系,目前计划是从Redis开始。 Re…...

更新丨三大模块升级,助力高效交付商业项目!
功能更新!本文将介绍最新升级的步进漫游、行业方案、VR漫游三个模块,让您更快更好的了解系统能力,为您带来更加便捷、高效的使用体验。步进漫游 离线导出步进式漫游系统,是基于全景图自动生成三维建模的解决方案,实现大…...
C++回顾(二)——const和引用
2.1 C中的const 2.1.1 C与C中const的比较 (1)C语言中的const C语言中 const修饰的变量是一个 常变量,本质还是变量,有自己的地址空间。 (2)C中的const 1、C中 const 变量声明的是一个真正的常量ÿ…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...
