树与二叉树与森林的相关性质
文章目录
- 树的度
- 树的性质
- 二叉树的性质
- 二叉树与森林
树的度
树的度指的是树内所有节点的度数的最大值。
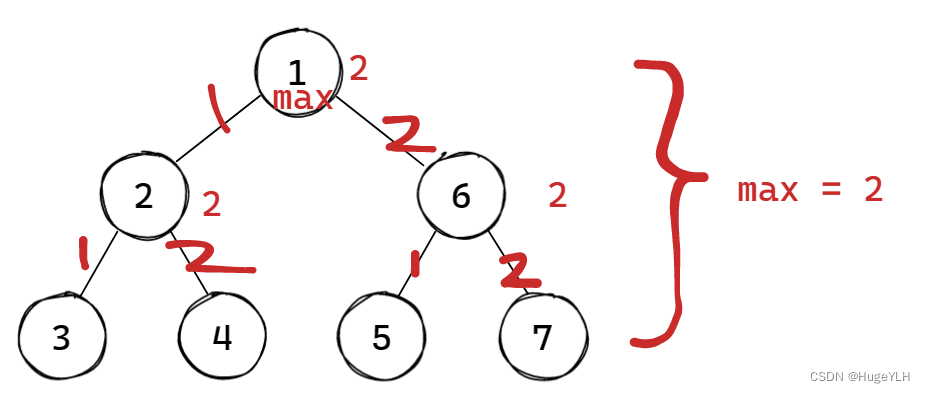
- 节点的度:节点所拥有的子树的数量。简单来说,我们直接数分支即可,例如下图:
在这颗二叉树中,节点2的度为2(他有两个子树),节点6的度为2(他也有两个子树),根节点1的度数也为2(有两个子树),其中叶子节点的度全部为0。
因此度为0的节点一定是叶子节点,度非零,则一定是非叶子节点。
- 树的度:树的度指的是所有的树中的内部节点的度数的最大值。如上图所示,所有节点的度数最大值为2(节点2和节点6和节点1),因此整个树的度为2
树的性质
- 树中所有的节点数等于树的度数+1。如上图所示,所有节点所具有的度数之和为 6,因此节点的总数: n = d+1
- 度为m的树中第 i 层至少有 m^(i-1) 个节点。图中树的度为2,因此m=2。第1层的节点数为1,第2层的节点数为2 ^ 1,第3层的节点数为 2 ^ 2
- 高度为 h 的 m 叉树最多有 (m ^ h - 1)/(m-1)。图中m=2,h=3,因此此树最多有 7 个节点。
- 具有 n 个节点的 m 叉树的最小高度为 logm(n(m-1)+1)。图中 n =7,m=2,因此此树的最小高度为 log2(8) ,因此高度为 3.
二叉树的性质
- 非空二叉树的叶子节点总数等于度为2的节点数+1。 上图中度为2的节点数为3,因此+1得叶子节点的个数为4
- 非空二叉树的第 k 层上最多有 2^k -1 个节点。上图中第 1 层有1个节点,第2层有两个,第3层有四个。
- 高度为 h 的二叉树最多有 2^ h-1 个节点。上图中高度 h =3,因此最多有 7个节点
- 具有n个节点的完全二叉树的高度为 log2(n+1) 或者 [log2(n)]+1。上图中有7个节点,因此高度为 log2(7+1) = 3
二叉树与森林
如何将一颗树转换为二叉树?
- 同一节点的各个孩子串联起来。
- 将每个节点的左右分支,从左往右除了第一个以外,全部删除
如何将二叉树转换为树?
- 二叉树从上往下分层,调整成水平方向,左孩子为一层的开始。
- 找到每层的双亲节点,方法为找到与这一层左孩子相连的上一个节点,即是这一层的公共双亲节点。
- 连接双亲节点之后,删除同层的相连关系。
图片演示:
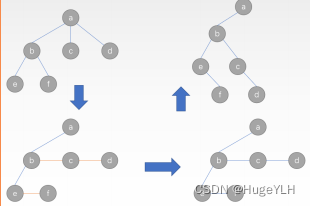
森林的概念:森林是 m 棵 互不相交的树的集合(不一定是二叉树)
如何将森林转换为二叉树?
- 首先将森林中每一棵树转换为二叉树。
- 然后将第二棵树作为第一颗树的右子树,第三棵树作为第二棵树的右子树,以此类推。
如何将二叉树转换为森林?
- 反复断开二叉树的根节点的右孩子子树,直到不存在右孩子指针为止。
森林与二叉树的转换:
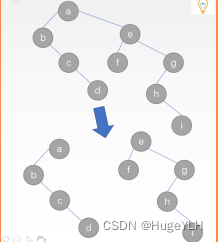
树与森林的遍历:
- 树的先序遍历等于它所对应二叉树的先序遍历
- 树的后序遍历等于它所对应二叉树的中序遍历
相关文章:

树与二叉树与森林的相关性质
文章目录树的度树的性质二叉树的性质二叉树与森林树的度 树的度指的是树内所有节点的度数的最大值。 节点的度:节点所拥有的子树的数量。简单来说,我们直接数分支即可,例如下图: 在这颗二叉树中,节点2的度为2&#…...

MySQL面试题
文章目录MySQL索引Mysql索引分类InnDB索引与MyISAM索引实现有什么区别一个表中如果没有创建索引,那么还会创建B树么?B树原理B树怎么来的B树 叶子节点和非叶子节点B树能存储多少数据?MySQL索引 Mysql索引分类 mysql 索引分为三类:…...

【蓝桥OJ—C语言】高斯日记、马虎的算式、第39级台阶
文章目录高斯日记马虎的算式第39级台阶总结高斯日记 题目: 大数学家高斯有个好习惯:无论如何都要记日记。 他的日记有个与众不同的地方,他从不注明年月日,而是用一个整数代替,比如:4210。 后来人们知道&am…...
:dtu数据集介绍及PatchMatchNet中加载数据部分代码解析)
基于深度学习的三维重建网络PatchMatchNet(二):dtu数据集介绍及PatchMatchNet中加载数据部分代码解析
目录 1.dtu数据集介绍 2. PatchMatchNet中数据加载模块详解(dtu_yao_eval.py) 1.dtu数据集介绍 dtu数据集下载地址:dtu...

一文3000字从0到1实现基于requests框架接口自动化测试项目实战(建议收藏)
requests库是一个常用的用于http请求的模块,它使用python语言编写,在当下python系列的接口自动化中应用广泛,本文将带领大家深入学习这个库 Python环境的安装就不在这里赘述了,我们直接开干。 01、requests的安装 windows下执行…...
【RockerMQ】001-RockerMQ 概述
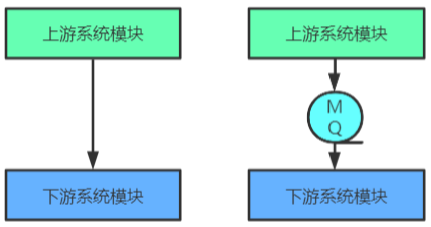
【RockerMQ】001-RockerMQ 概述 文章目录【RockerMQ】001-RockerMQ 概述一、MQ 概述1、MQ 简介2、MQ 用途限流削峰异步解耦数据收集3、常见 MQ 产品概述对比4、MQ 常见协议二、RocketMQ 概述1、简介2、发展历史一、MQ 概述 1、MQ 简介 MQ,Message Queue࿰…...

阿里是如何做Code Review的?
作为卓越工程文化的一部分,Code Review其实一直在进行中,只是各团队根据自身情况张驰有度,松紧可能也不一,这里简单梳理一下CR的方法和团队实践。 一、为什么要CR 提前发现缺陷 在CodeReview阶段发现的逻辑错误、业务理解偏差、性…...

内核调试:一次多线程调试与KASAN检测实例
内核调试:一次多线程调试与KASAN检测实例1. 环境说明2. 问题描述3. 问题排查与定位3.1 线程并发问题(减少线程数)3.2 轻量地跟踪对象的分配与释放3.3 检查空指针与潜在修改者3.4 KASAN检查4. 总结博主最近遇到一个非常顽固的多线程BUG&#x…...
Java - 数据结构,队列
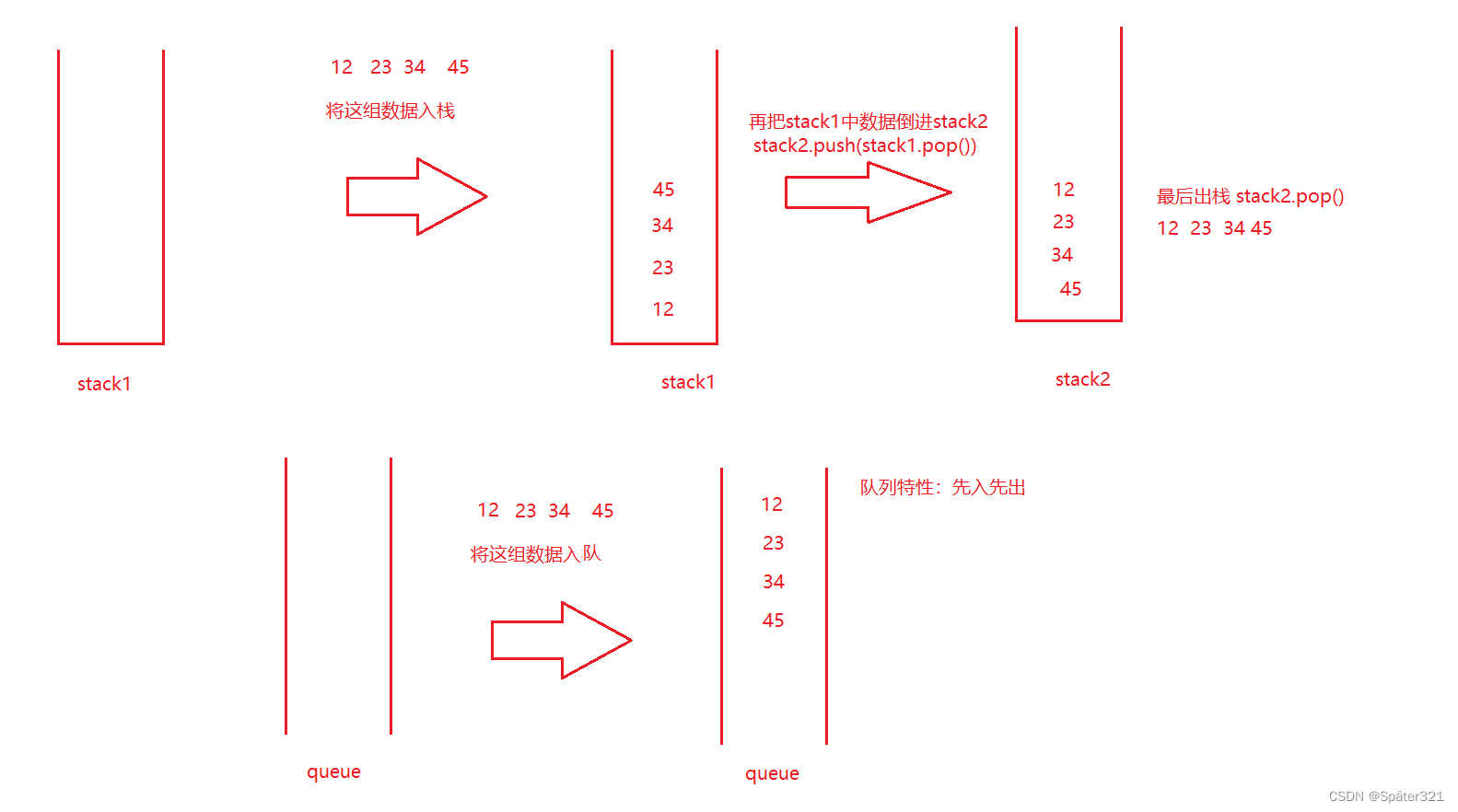
一、什么是队列 普通队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(FirstIn First Out) 入队列:进行插入操作的一端称为队尾(Tail/Rear) 出队列…...
ccc-pytorch-感知机算法(3)
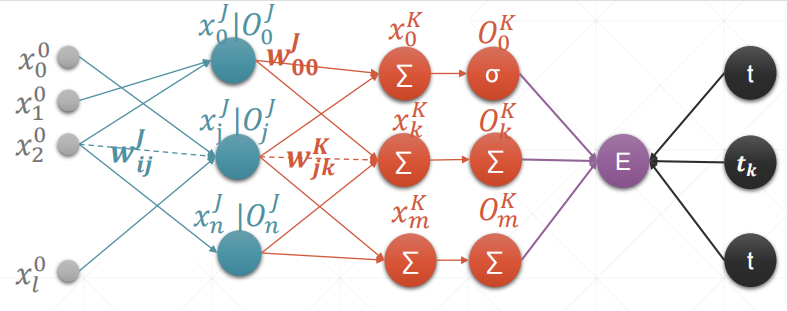
文章目录单一输出感知机多输出感知机MLP反向传播单一输出感知机 内容解释: w001w^1_{00}w001:输入标号1连接标号0(第一层)x00x_0^0x00:第0层的标号为0的值O11O_1^1O11:第一层的标号为0的输出值t:真实…...

LeetCode 225.用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。实现 MyStack 类:void push(int x) 将元素 x 压入栈顶。int pop() 移除并返回栈顶元素。int top() …...

【面试】spring控制反转IOC
目录一.说明二.ioc的概念和作用三.优点四.实现机制五.IOC和DI的区别六.设计原则一.说明 1.ioc的概念2.ioc的作用3.ioc的优点4.ioc的实现机制 二.ioc的概念和作用 1.全称Inversion of Control2.控制:创建对象的控制权3.反转:以前对象是程序员主动去new…...

Spring 事务管理详解及使用
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

LeetCode 232.用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):实现 MyQueue 类:void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开头的元…...
go面向对象思想封装继承多态
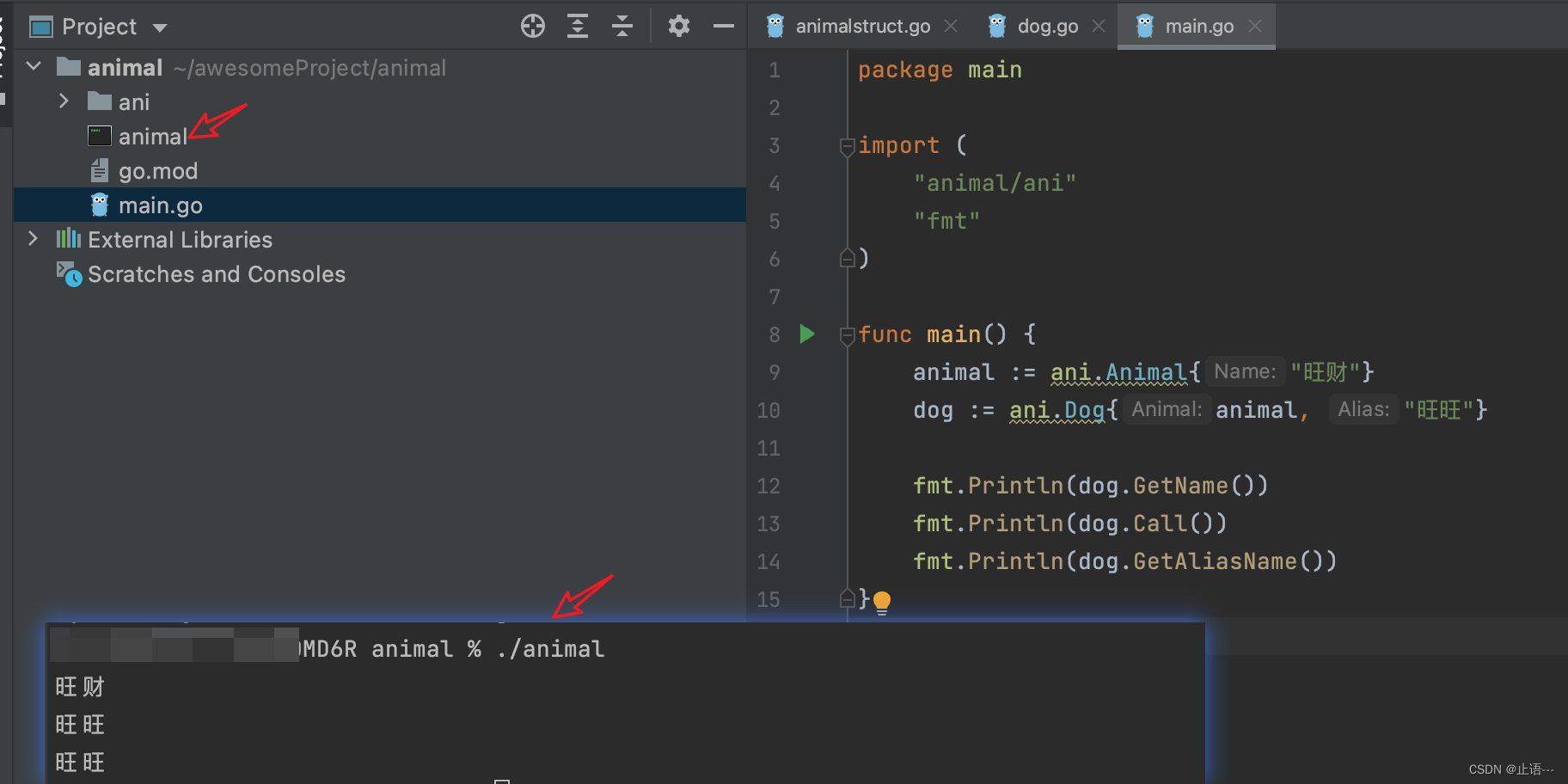
go貌似都没有听说过继承,当然这个继承不像c中通过class类的方式去继承,还是通过struct的方式,所以go严格来说不是面向对象编程的语言,c和java才是,不过还是可以基于自身的一些的特性实现面向对象的功能,面向…...
【网络原理9】HTTP响应篇
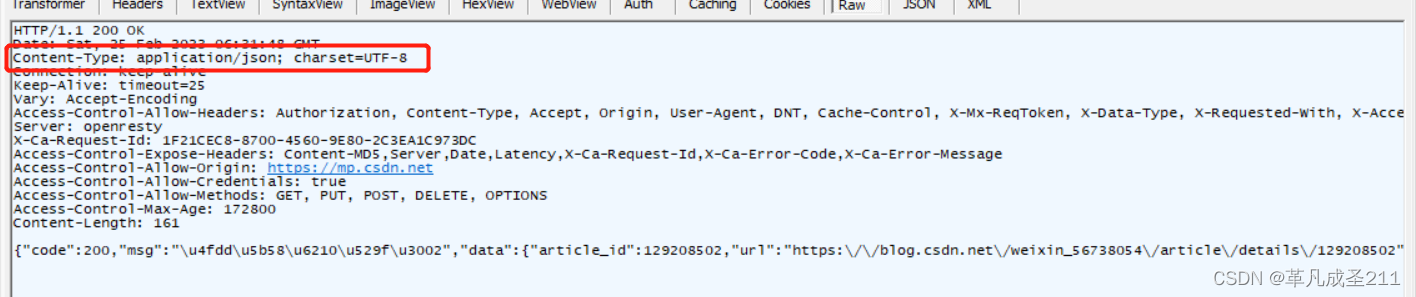
在前两篇文章当中,已经分别介绍了HTTP是什么,以及常见的请求头当中的属性。【网络原理7】认识HTTP_革凡成圣211的博客-CSDN博客HTTP抓包,Fiddler的使用https://blog.csdn.net/weixin_56738054/article/details/129148515?spm1001.2014.3001.…...

SpringCloud之Seata(二)
4.Seata如何应用于项目? 安装seata及修改配置 4.1 官网下载Seata安装包 4.2 修改seata/config.txt 4.2.1 修改存储方式 store.db.dbTypemysql store.db.driverClassNamecom.mysql.jdbc.Driver store.db.urljdbc:mysql://你的IP:3306/seata?useUnicodetrue sto…...

【Redis-入门阶段】基本数据结构
Redis支持多种数据结构,包括字符串、列表、哈希、集合和有序集合。这些数据结构在Redis中被称为键值对,其中键是一个字符串,值可以是一个字符串、列表、哈希、集合或有序集合。接下来,我们将详细介绍这些数据结构的使用方法。字符…...
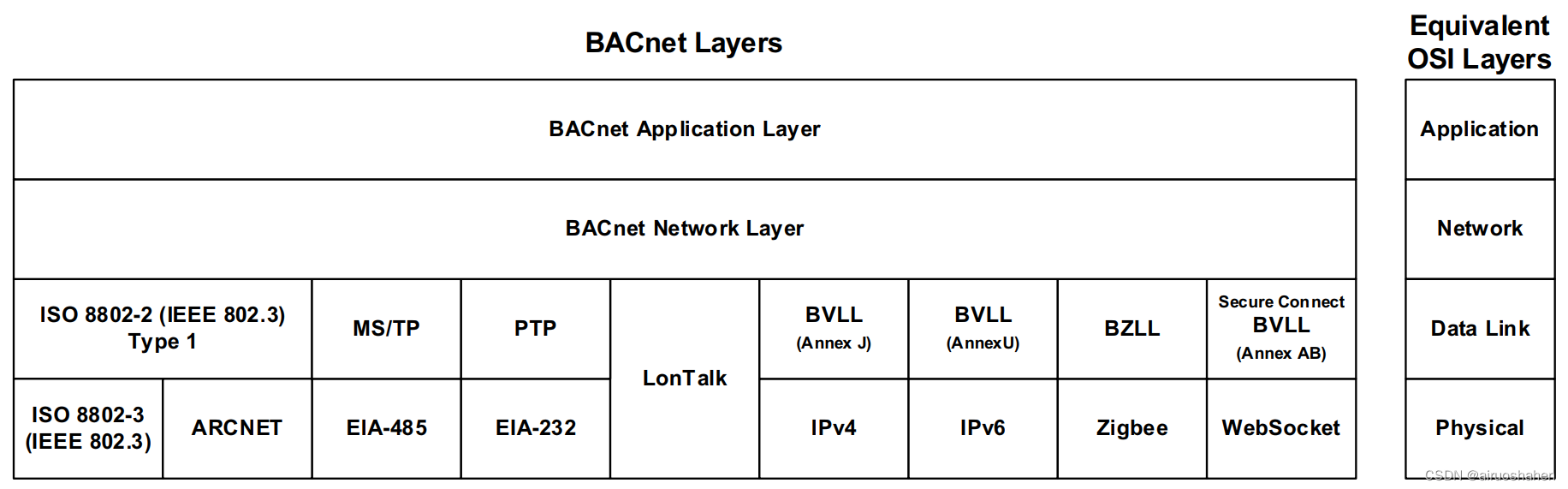
BACnet协议详解————MS/TP物理层,数据链路层和网络层
文章目录写在前面1 物理层2 数据链路层MSTP的流程如下noteMS/TP帧格式3 网络层写在前面 这周加更一篇,来弥补一下之前落下的进度。简单的说两句,之前讲应用层的时候,只是跟官方的手册来同步一下,但是从个人理解来说,自…...

Tomcat
Tomcat 1 简介 1.1 什么是Web服务器 Web服务器是一个应用程序(软件),对HTTP协议的操作进行封装,使得程序员不必直接对协议进行操作,让Web开发更加便捷。主要功能是"提供网上信息浏览服务"。 Web服务器是安…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
