数据结构与算法-树
树
- 🎈1.树和二叉树
- 🎈2.树
- 🔭2.1树的定义
- 🔭2.2树的4种表示方法
- 🔭2.3树的基本术语
- 🔭2.4树的抽象数据类型定义
- 🎈3.二叉树
- 🔭3.1二叉树的定义
- 🔭3.2二叉树的抽象数据类型定义
- 🔭3.3满二叉树
- 🔭3.4完全二叉树
- 🔭3.5完全二叉树的特点
- 🔭3.6二叉树的性质
- 🔭3.7二叉树的存储结构
- 🔭3.8完全二叉树的顺序存储
- 🔭3.9一般二叉树的存储结构
- 🔭3.10二叉树的链式存储结构
- 🎈4.二叉树的类定义及其实现
- 🔭4.1二叉树的类定义
- 🔭4.2二叉树的实现
- 📖4.2.1创建二叉树
- 📖4.2.2计算二叉树的高度
- 📖4.2.3计算二叉树的树叶数
- 📖4.2.4查找二叉树
🎈1.树和二叉树
树结构是一类重要的
非线性结构,树型结构是结点之间有分支,并且具有明显的层次关系的结构,它类似于自然界中的树。树结构在客观世界是大量存在的,例如行政组织机构和人类社会的家谱都可以用树来形象表示。
🎈2.树
🔭2.1树的定义
树是
n(n>=0)个结点的有限集T。
若n=0,称为空树。
若n>0,则它满足以下两个条件:
(1).有且仅有一个特定的称为根的结点。
(2).其余结点可以分为m(m>=0)个互不相交的有限集T1,T2,T3......Tm,其中,每个集合本身又是一棵树,并称为根的子树。
🔭2.2树的4种表示方法

🔭2.3树的基本术语

- 结点:树中每个元素对应一个结点。每个结点包含一个数据元素及若干指向子树的分支。例如,图中的树有11个结点,结点D包含3个分支。
- 结点的度:结点所拥有的子树的个数称为结点的度。例如,结点A和D的度均为3,结点B的度为2,结点C的度为1,结点F的度为0。
- 叶子结点:度为0的结点称为叶子结点(或称树叶),又称终端结点。例如,上图所示,E,F,G,H,I,K都是叶子结点。
- 分支结点:度不为0的结点称为分支结点,又称非终端结点。例如,上图所示的树,A,B,C,D,J都是分支结点。
- 树的度:树中所有结点的最大度数称为树的度。例如,图所示的树的度为3.
- 双亲结点:若结点X有孩子,则X为孩子的双亲结点,简称双亲。例如,在图所示的树中,结点H,I,J的双亲是D,根结点A没有双亲,树中只有根结点没有双亲。
- 孩子结点:若结点X由子树,则子树的根结点即为结点X的孩子结点,简称孩子。例如,结点D有三个孩子H,I,J。
- 兄弟结点:同一双亲的孩子结点称为兄弟结点,简称兄弟。例如,结点H,I,J为兄弟。
- 堂兄弟结点:在树中的层次相同,但双亲不同的结点称为堂兄弟,简称堂兄。例如,结点F,G,H为堂兄弟。
- 祖先结点:从根结点到结点X所经过分支上的所有结点,都称为X的祖先结点,简称祖先。例如,K的祖先为A,D,J
- 子孙结点:结点X的孩子,以及这些孩子的孩子都是X的子孙结点。例如,结点D的子孙为H,I,J,K
- 结点的层次:根结点的层次为1,根结点的孩子的层次为2,根结点的孩子的孩子的层次为3,依次类推。
- 树的深度:树中结点的最大层次称为树的深度,也称树高。空树的深度为0,只有一个根结点的树的深度为1,图所示的树的深度为4.
- 路径:从树的某个结点X到其子孙结点Y所经过的路线叫做路径,路径上经过的边的数称为路径长度。由于树中无回路,所以树的路径是唯一的。如图所示的树中,从A到结点K的路径是A,D,J,K,路径长度为3.
- 森林:m(m>=)棵互不相交的树构成的集合称之为森林。
🔭2.4树的抽象数据类型定义
ADT Tree{
数据对象D:D为性质相同的数据元素的集合
数据关系R:
若D为空集,则称为空树。
若D仅有一个数据元素,则R=空集,否则R!=空集。
(1).在D中存在唯一的称为根的数据元素root,它在关系R下无前驱。
(2).存在D-{root}的一个划分{D1,D2,...,Dm}(m>0),且对于(1<=i<=m),存在唯一的数据元素Xi属于Di,有(root,Xi)属于R.
(3).对应于D-{root}的一个划分,r-{(root,x1),(root,x2),...,(root,Xm)}存在唯一的一个划分{R1,R2,...,Rm}(m>0),对于(1<=i<=m),Ri是Di上的二元关系,(xi,Ri)(i=1,2,...,m)是一棵符合本定义的树,称为根root的子树。
基本操作:
InitTree(&t):构造一棵空树
DestroyTree(&t):销毁一棵树
Parent(t,e):求结点e的双亲结点
Sons(t,e):求结点e有所有孩子结点
LeftChild(t,e):返回结点e的右兄弟最左孩子
RightSibling(t,e):返回结点e的右兄弟结点
TraraverseTree(t,visit()):以visit()函数访问树中每个结点
DepthTree(t):返回树的深度
}ADT Tree
🎈3.二叉树
🔭3.1二叉树的定义
二叉树是由
n(n>=0)个结点构成的有限集合,该集合或者为空集,此时称为空二叉树,或由一个根结点及两棵互不相交的左右子树组成,并且左右子树均是二叉树。二叉树的子树有左右之分,其次序不能颠倒。
二叉树的定义也是一个递归定义,二叉树可以是空集合,根可以有空的左子树或空的右子树。。二叉树不是树的特殊情况,它们是两个概念。二叉树中即使只有一棵子树也要进行区分,说明它是左子树,还是右子树,这是二叉树与树的最主要的差别。“二叉树是结点度为2的树”的说法是错误的。二叉树的5种基本形态:
🔭3.2二叉树的抽象数据类型定义

🔭3.3满二叉树
一棵深度为
k且有2k-1个结点的二叉树称为满二叉树。满二叉树的特点是每一层上结点数都是最大结点数。如图所示,是一棵深度为4的满二叉树。
🔭3.4完全二叉树
可以对满二叉树的结点进行顺序编号,约定编号从根结点开始,自上而下,从左至右(称为层序编号)。
如果一棵深度为k且具有n个结点的二叉树,它的每个结点都与深度为k的满二叉树中的顺序编号1~n的结点一一对应,则称这棵二叉树为完全二叉树。
🔭3.5完全二叉树的特点
- 叶子结点只能在第
k层和第k-1层上出现。 - 对于任意结点,若其右子树的深度为
l,则其左子树的深度为l或l+1。 - 度为
1的结点数为0或1。当结点的总数为奇数时,度为1的结点数为0,当结点的总数为偶数时,度为1的结点数为1.
🔭3.6二叉树的性质
- 二叉树的第
i层上至多有2i-1(i>=1)个结点。 - 深度为
k的二叉树最多有2k-1(k>=1)个结点。 - 对于任何一棵二叉树,如果其叶子结点数为
n0,度为2的结点数为n2,则n0=n2+1.
性质3推论:对于任何一棵k叉树,如果叶子结点数为n0,度为1,2,...k的结点数分别为n1,n2,...,nk,则n0=n2+2n3+3n4+...(k-1)nk+1.
例:一棵三叉树中,已知度为3的结点数等于度为2的结点数,且叶子结点数为10,则度为3的结点为多少?
n0 = n2+2n3+1=3n3+1
n3 = 3
- 一棵具有n个结点的完全二叉树的深度为[log2n]+1(以2为底,n的对数)。

🔭3.7二叉树的存储结构
二叉树的顺序存储结构是用一组地址连续的存储单元来存放二叉树的数据元素。
📝二叉树的顺序存储结构类型定义如下:
#define MaxSize 100 //二叉树的最大存储容量
typedef ElemType SqBiTree[MaxSize] //用数组存储二叉树的数据元素
SqBiTree bt;
🔭3.8完全二叉树的顺序存储
在用数组存储二叉树时,必须确定树中各数据元素的存放次序,使各数据元素的相应位置反映出数据元素之间的逻辑关系用一组地址连续的存储单元依次自上而下、自左而右地存储完全二叉树的结点元素。
🔭3.9一般二叉树的存储结构
在采用顺序存储时,应采用完全二叉树的编号方式,没有编号的结点在对应的位置上用#表示。
注:对于完全二叉树而言,采用顺序存储结构方式是十分合理的,它能够充分利用存储空间,但对于一般的二叉树而言,这种存储方式必然会造成大量空间浪费。在最坏的情况下,一棵深度为k且只有k个单分支二叉树,却需要长度为2k-1的一维数组来存储。因此,一般二叉树常采用链式存储方式。
🔭3.10二叉树的链式存储结构
根据二叉树的定义,二叉树的每个结点可以有两个分支,分别指向及诶单的左子树和右子树。在二叉树中,标准存储方式的结点结构如图所示:
其中,data表示数据域,用来存放数据元素信息。
lchild表示左指针域,用来存放指向左孩子的指针,当左孩子不存在时为空指针。
rchild表示右指针域,用来存放指向右孩子的指针,当右孩子不存在时为空指针。
这种链式存储结构通常称为二叉链表。
二叉链表的结点类型定义:
typedef struct BitNode
{ElemType data;//数据元素信息BitNode *lchild;//指向左孩子结点BitNode *rchild;//指向右孩子结点
}BitNode;
由二叉树的链式存储结构可知,对于具有n个结点的二叉树,每个结点有两个指针域,共有2n个指针域,其中n-1个非空链域,n+1个空链域。
🎈4.二叉树的类定义及其实现
🔭4.1二叉树的类定义
#include <iostream>
using namespace std;
typedef struct BitNode
{char data;BitNode* lchild;BitNode* rchild;
}BitNode;
class BiTree
{
private:BitNode* bt;void Rcreate(BitNode*& t);//递归创建二叉树void PreTraverse(BitNode* t);//先序遍历递归函数void InTraverse(BitNode* t);//中序遍历递归函数void PostTraverse(BitNode* t);//后序遍历递归函数int BTNodeDepth(BitNode* t);//计算二叉树的树高递归函数int BTNodeLeaf(BitNode* t);//计算二叉树树叶数递归函数BitNode* SearchNode(BitNode* t, char x);//查找值等于x的结点递归函数
public:BiTree(){bt = NULL;//创建空树}void RcreateBiTree();//创建二叉树void PreTraverseBiTree();//先序遍历二叉树void InTraverse();//中序遍历二叉树void PostTraverse();//后序遍历二叉树int BTNodeDepthBiTree();//计算二叉树的树高int BTNodeLeafBiTree();//计算二叉树的叶子数BitNode* SearchNodeBit(char x);//查找值等于x的结点
};
🔭4.2二叉树的实现
📖4.2.1创建二叉树
Rcreate()函数递归创建二叉树,其过程为:读入字符ch,若ch=='.',则创建空二叉树,若ch!='.',则先创建左子树,再创建右子树。
void BiTree::Rcreate(BitNode*& t)
{char ch;cin >> ch;if (ch == '.')t = NULL;else{t = new BitNode;//申请空间t->data = ch;Rcreate(t->lchild);//递归创建左子树Rcreate(t->rchild);//递归创建右子树}
}
void BiTree::RcreateBiTree()
{BitNode* t;Rcreate(t);//递归创建二叉树bt = t;//将根结点指针赋值给私有成员bt
}
📖4.2.2计算二叉树的高度
BTNodeDepth()函数递归计算二叉树的树高,其过程为:判断二叉树t是否为空树,若为空树,树高则为0。若为非空树,则计算左子树的高度m和右子树的高度n;m>=n,返回m,否则返回n.

int BiTree::BTNodeDepth(BitNode* t)
{if (t == NULL)return 0;else{int m = 1 + BTNodeDepth(t->lchild);//计算左子树树高度int n = 1 + BTNodeDepth(t->rchild);//计算右子树树高度if (m >= n)//比较左右子树高度return m;elsereturn n;}
}
int BiTree::BTNodeDepthBiTree()
{//计算二叉树的高度BitNode* p = bt;return BTNodeDepth(p);//调用计算二叉树高度的递归函数
}
📖4.2.3计算二叉树的树叶数
BTNodeLeaf()计算二叉树的树叶数,其过程为:判断t是否为空树,若为空树,则树叶数为0;若为非空树,则计算左子树的树叶数m和右子树的树叶数n,m+n=0时返回1,m+n!=0时返回m+n.
int BiTree::BTNodeLeaf(BitNode* t)
{//递归算法计算二叉树的树叶数if (t == NULL)return 0;else{int m = BTNodeLeaf(t->lchild);//计算左子树的树叶数int n = BTNodeLeaf(t->rchild);//计算右子树的树叶数if (m + n == 0)return 1;elsereturn m + n;}
}
int BiTree::BTNodeLeafBiTree()
{//计算二叉树的树叶数BitNode* p = bt;//读取私有成员指针btreturn BTNodeLeaf(p);//调用二叉树的树叶数的递归函数
}
📖4.2.4查找二叉树
SearchNode()函数在二叉树t中查找值等于x的结点,若找到该结点时返回其首地址,否则返回NULL.判断t是否为空树,若为空树,则返回NULL,若为非空树,则在t->data==x时返回t,在t->data!=x时,在左子树中查找,否则在右子树中查找。
BitNode* BiTree::SearchNode(BitNode* t, char x)
{BitNode* p;if (t == NULL)return NULL;if (t->data == x)return t;else{p = SearchNode(t->lchild,x);//递归查找左子树if (p != NULL)return p;elsereturn SearchNode(t->rchild, x);//递归查找右子树}
}
BitNode* BiTree::SearchNodeBit(char x)
{BitNode* p = bt;return SearchNode(p, x);
}
好啦,关于二叉树的知识到这里并没有结束,后期会继续更新二叉树的相关知识,欢迎大家持续关注、点赞和评论!❤️❤️❤️
相关文章:

数据结构与算法-树
树 🎈1.树和二叉树🎈2.树🔭2.1树的定义🔭2.2树的4种表示方法🔭2.3树的基本术语🔭2.4树的抽象数据类型定义 🎈3.二叉树🔭3.1二叉树的定义🔭3.2二叉树的抽象数据类型定义&a…...
 Error: Infinite redirect in navigation guard)
【Bug排查】Uncaught (in promise) Error: Infinite redirect in navigation guard
记一次Bug排查 今日在做尚硅谷的商品甄选项目时,遇到无法登录的问题:报错Uncaught (in promise) Error: Infinite redirect in navigation guard 一开始我去搜CSDN,都说是路由的问题,我对前端也不了解,试着改了一下&…...

ant使用第三方任务
ant提供了一个插件机制来使用第三方的任务。为了使用第三方的任务,需要做两步: 将它们的实现放在ant能找到的地方。声明任务 声明任务的几种方法: 声明一个任务:利用<taskdef name"taskname" classname"Impl…...
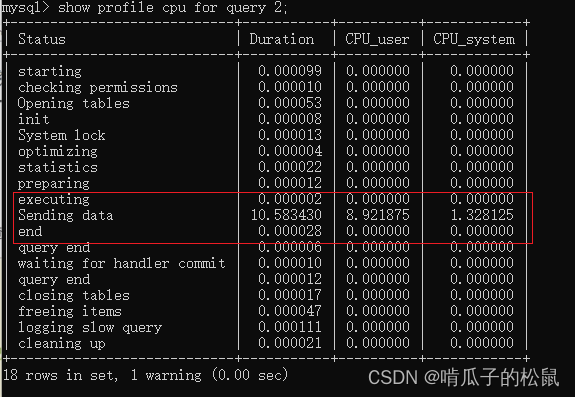
MySQL 性能分析
MySQL 性能分析 对 mysql 进行性能分析,主要就是提升查询的效率,其中索引占主导地位。对 mysql 进行性能分析主要有如下几种方式: 方式一:查看 sql 执行频次 show global status like ‘Com_______’; // global 表示全局 show s…...

【MySQL】数据库——库操作
文章目录 1. 创建数据库[IF NOT EXISTS] 的使用 2. 删除库3. 数据库的编码问题查看系统默认支持的字符集查看系统默认支持的校验集只查看 database的校验集指定编码创建数据库修改字符集修改校验集验证规则对数据库的影响utf8_general_ci ——不区分大小写utf8_bin ——区分大小…...

Python 轻量 ORM peewee 上手
介绍 有时候需要用 Python 直接操作数据库, 手工撸 SQL 倒也不是不能行, 但是总觉得有点背离了 人生苦短, 我用 Python 的初心, 习惯了 SQLAlchemy 的直接操作后, 就变懒了. 但是对于比较简单的数据库操作场景, 再跑一套 SQLAlchemy 又显得有些臃肿, 这次上手轻量 Python ORM …...

微信小程序开发的OA会议之会议,投票,个人中心的页面搭建及模板
目录 一.自定义组件 1.1.创建 1.2.定义 1.3.编写 1.4.使用 二.会议 2.1.数据 2.2.显示 2.3. 样式 三.个人中心 3.1.页面 3.2.样式 四.投票 4.1.引用 4.2.数据 4.3.页面 4.4.样式 好啦今天就到这里了,希望能帮到你哦!!&…...
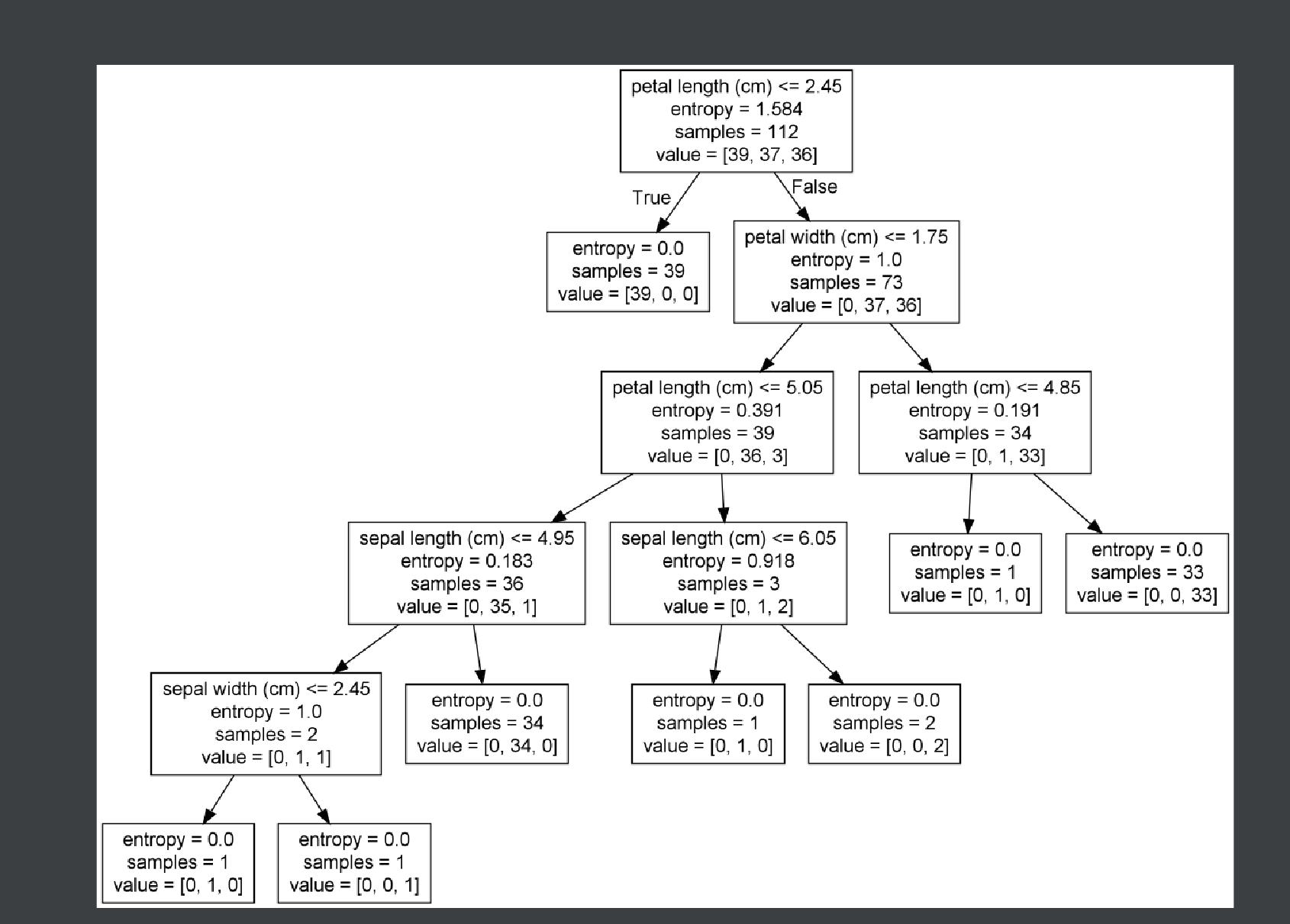
决策树-入门
1、认识决策树 决策树思想的来源非常朴素,程序设计中的条件分支结构就是if-then结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法 怎么理解这句话?通过一个对话例子 想一想这个女生为什么把年龄放在最上面判断!&a…...

使用Redis发布订阅模式实现 Session共享
其实并不是实现session共享,而是通过redis的发布订阅,让所有集群的服务器,都让自己的session发送一下消息。比如说userId在第35台服务器上, 有100台服务器,那么第1台服务器收到消息,需要通知userId…...
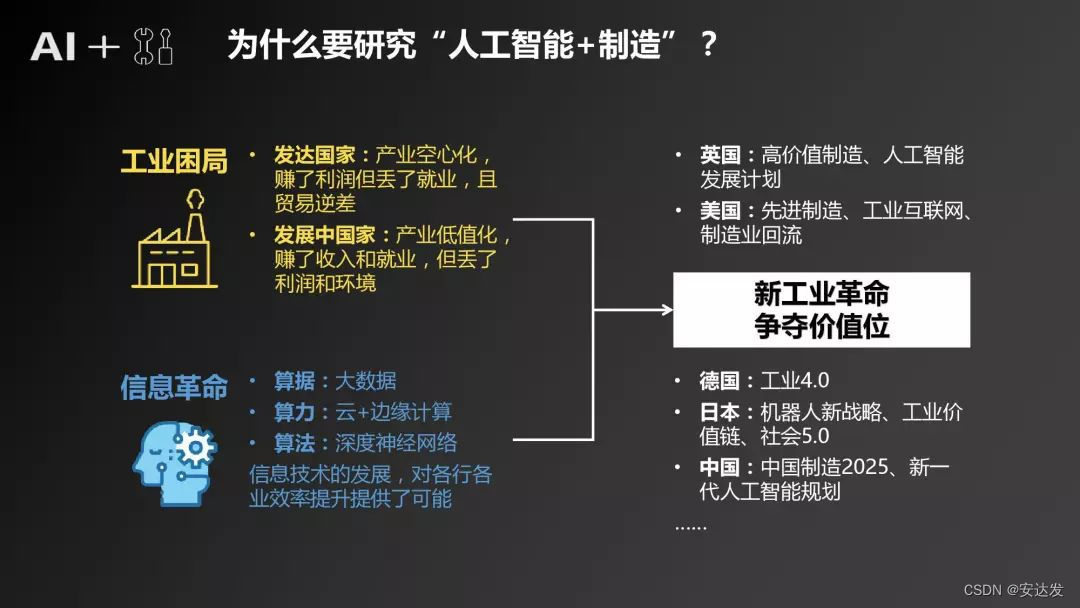
安达发|AI在APS生产计划排程系统中的应用与优势
随着科技的不断发展,人工智能(AI)已经在许多领域取得了显著的成果。在生产管理计划系统中,AI技术的应用也日益受到关注。本文将探讨如何将AI人工智能用在生产管理计划系统上,以提高生产效率、降低成本并优化资源配置。…...
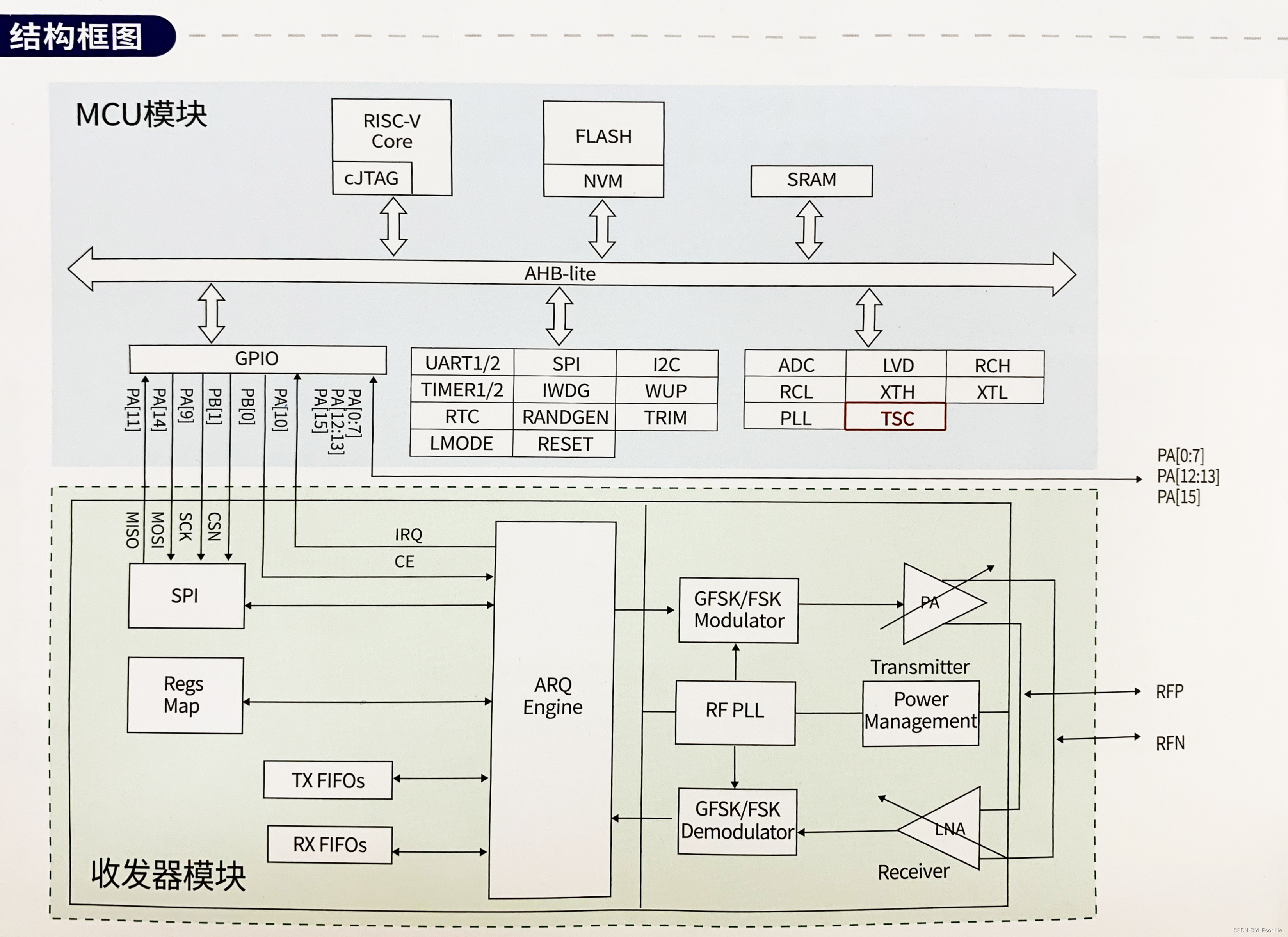
国产低功耗MCU芯片:Si24R03
Si24R03集成了基于RISC-V核的低功耗MCU和工作在2.4GHz ISM频段的无线收发器模块,是一款高度集成的低功耗SOC片。 应用领域: 1、物联网 2、智N门锁 3、电机控制 4、消费电子 5、工业控制 其无线收发器模块是专为低功耗无线场合设计,在关…...

【Java】学生管理系统项目演示
目录 学生管理系统 学生管理系统代码思路分析 nextLine() 和 nextInt() 区别 学生管理系统 需求:实现对学生的增删改查功能,学生(学号,姓名,年龄,地址)字段 学生管理系统代码思路分析 定义学…...

Rust错误处理
返回值和错误处理 panic 深入剖析 主动调用 fn main() {panic!("crash and burn"); }backtrace 栈展开 panic 时的两种终止方式 当出现 panic! 时,程序提供了两种方式来处理终止流程:栈展开和直接终止 何时该使用 panic! 先来一点背景知…...

Golang操作数据库简单示例
目录 准备工作准备数据创建项目连接数据库查询数据修改数据插入数据删除数据释放资源完整代码最终执行结果 准备工作 在开始之前,你需要确保自己安装了Golang的编程环境,安装MySQL数据库,有一个可以用于编写代码的编辑器或IDE工具。我在这里…...

亚马逊测评,买家号支付不了、砍单率高是什么问题,需要怎么解决
下半年旺季很多卖家都在使用自养号测评给产品冲一波权重,但是很多朋友会遇到下不了单或者砍单率过高等问题。有人以为是支付卡的问题,也有人觉得是IP被关联了。其实他们讲的也没错,但是,亚马逊风控不会针对某个点去进行检测&#…...
)
B. Jellyfish and Game-Codeforces Round 902 (Div. 2)
B. Jellyfish and Game 交换k轮使得第一个同学拥有数值总数最大; 很容易看出这道题需要判断k奇偶数。 当k是奇数时可以看作第一个同学操作一轮。 k为偶数可以看作两个同学各操作一轮。 #include<iostream> #include<vector> #include<algorithm>…...

Linux下的命令行参数和环境变量
命令行参数 什么是命令行参数 命令行参数是指在执行命令行程序时,给程序传递的额外参数。在Linux终端中,命令行参数通常通过在命令后面添加空格分隔的参数来传递。 Linux下以main函数举例说明 #include<stdio.h>int main(int argc char* argv[])…...
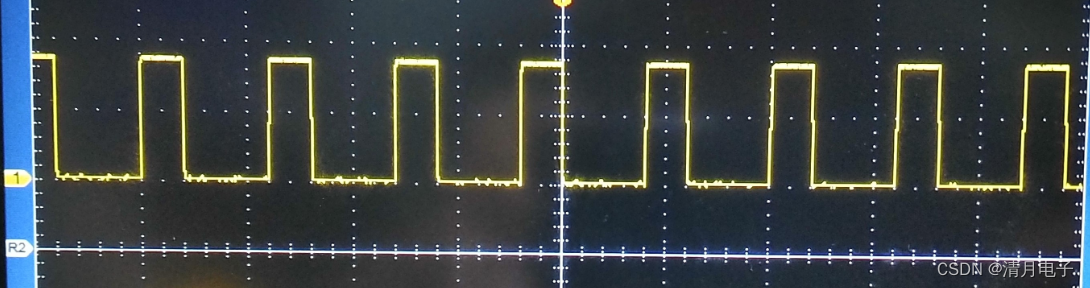
语音芯片KT142C两种音频输出方式PWM和DAC的区别
目录 语音芯片KT142C两种音频输出方式PWM和DAC的区别 一般的语音芯片,输出方式,无外乎两种,即dac输出,或者PWM输出 其中dac的输出,一般应用场景都是外挂功放芯片,实现声音的放大,比如常用的音箱…...

Kotlin 协程的挂起和阻塞的区别
一,简介 Kotlin协程引入了非常强大的异步编程模型,通过挂起而不是阻塞来实现并发操作。以下是有关Kotlin协程挂起和阻塞的详细介绍: 挂起(Suspending): 挂起是指一个协程的执行可以在不阻塞线程的情况下暂…...
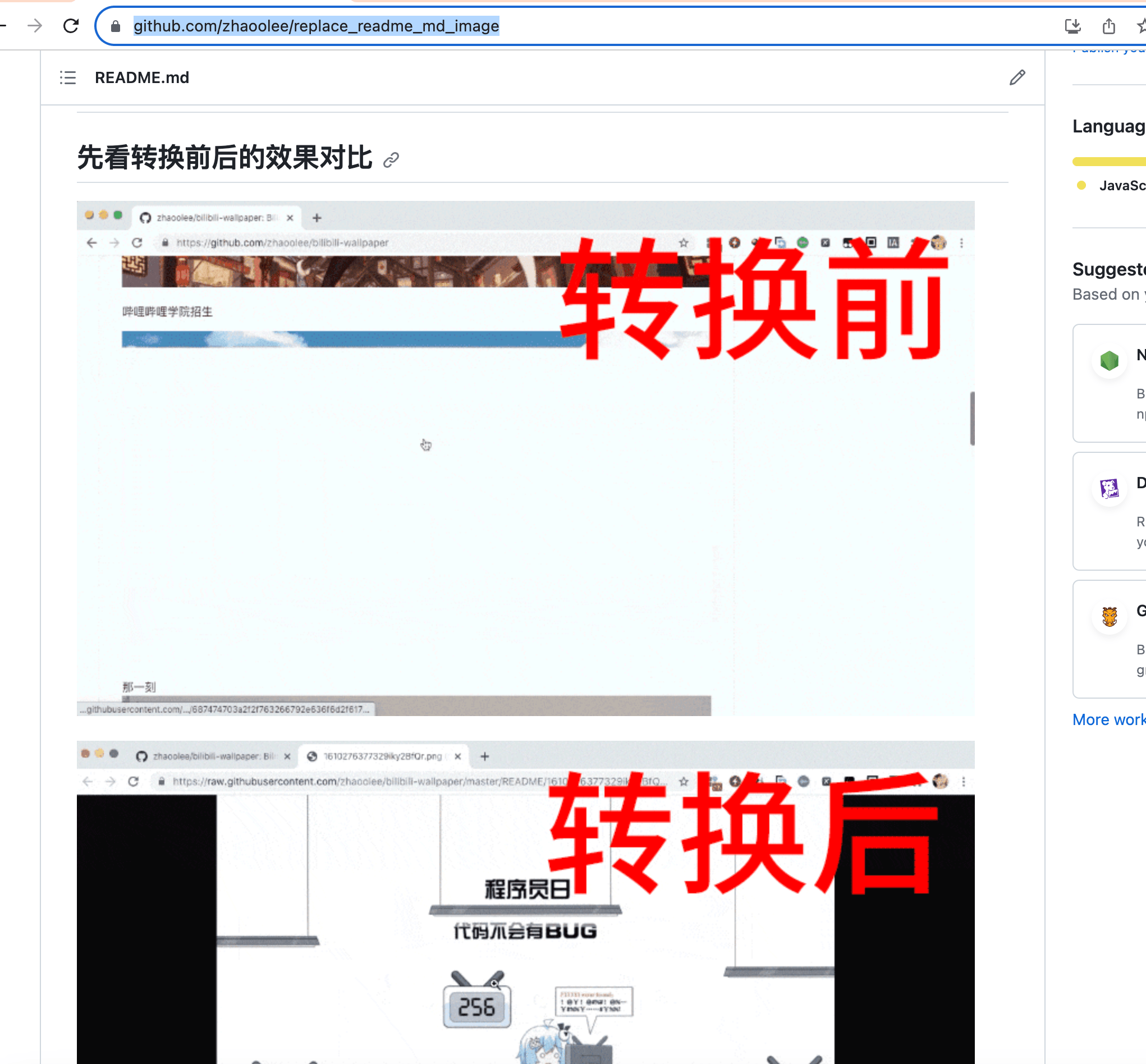
解决Github Markdown图片显示残缺的问题
title: 解决Github Markdown图片显示残缺的问题 tags: 个人成长 categories:杂谈 在Github存放Markdown文档,如果图片没有存放在Github服务器上,github会尝试生成Github图片缓存,使用Github图片缓存,进行实际的展示。但比较蛋疼的…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...







