【TensorFlow1.X】系列学习笔记【基础一】
【TensorFlow1.X】系列学习笔记【基础一】
大量经典论文的算法均采用 TF 1.x 实现, 为了阅读方便, 同时加深对实现细节的理解, 需要 TF 1.x 的知识
文章目录
- 【TensorFlow1.X】系列学习笔记【基础一】
- 前言
- 线性回归
- 非线性回归
- 逻辑回归
- 总结
前言
本篇博主将用最简洁的代码由浅入深实现几个小案例,让读者直观体验深度学习模型面对线性回归、非线性回归以及逻辑回归的处理逻辑和性能表现。【代码参考】
线性回归
线性回归是一种常见回归分析方法,它假设目标值与特征之间存在线性关系。线性回归模型通过拟合线性函数来预测目标值。线性回归模型的形式比较单一的,即满足一个多元一次方程。常见的线性方程如: y = w × x + b {\rm{y}} = w \times x + b y=w×x+b,但是观测到的数据往往是带有噪声,于是给现有的模型一个因子 ε \varepsilon ε,并假设该因子符合标准正态分布: y = w × x + b + ε {\rm{y}} = w \times x + b + \varepsilon y=w×x+b+ε。对于线性模型,深度学习可以通过构建单层神经网络来描述,这个单层神经网络通常被称为全连接层(Fully Connected Layer)或线性层(Linear Layer),其中每个神经元都与上一层的所有神经元相连接,且没有非线性激活函数。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt# 随机生成100个数据点,服从“0~1”均匀分布
x_data = np.random.rand(100)# 提升维度(100)-->(100,1)
x_data = x_data[:, np.newaxis]# 制作噪声,shape与x_data一致
noise = np.random.normal(0, 0.02, x_data.shape)# 构造目标公式
y_data = 0.8 * x_data + 0.1 + noise# 输入层:placeholder用于接收训练的数据
x = tf.placeholder(tf.float32, [None, 1], name="x_input")
y = tf.placeholder(tf.float32, [None, 1], name="y_input")# 构造线性模型
b = tf.Variable(0., name="bias")
w = tf.Variable(0., name="weight")
out = w * x_data + b# 构建损失函数
loss = 1/2*tf.reduce_mean(tf.square(out - y))
# print(loss)# 定义优化器
optim = tf.train.GradientDescentOptimizer(0.1)
# print(optim)# 最小化损失函数
train_step = optim.minimize(loss)# 初始化全部的变量
init = tf.global_variables_initializer()# 训练迭代
with tf.Session() as sess:sess.run(init)for step in range(2000):sess.run([loss, train_step], {x: x_data, y: y_data})if step % 200 == 0:w_value, b_value, loss_value = sess.run([w, b, loss], {x: x_data, y: y_data})print("step={}, k={}, b={}, loss={}".format(step, w_value, b_value, loss_value))prediction_value = sess.run(out, feed_dict={x: x_data})plt.figure()
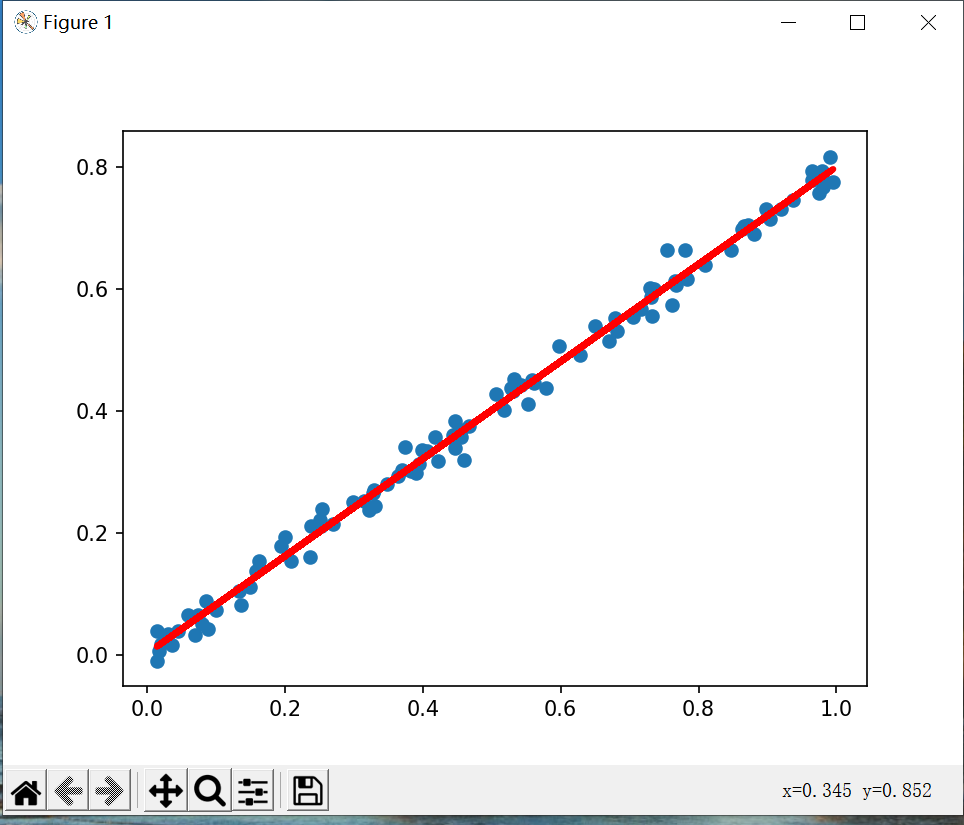
plt.scatter(x_data, y_data)
plt.plot(x_data, prediction_value, "r-", lw=3)
plt.show()
非线性回归
非线性回归也是一种常见回归分析方法,它假设目标值与特征之间存在非线性关系。与线性回归不同,非线性回归模型可以拟合复杂的非线性关系。通过拟合非线性函数到数据中,非线性回归模型可以找到最佳的函数参数,以建立一个能够适应数据的非线性关系的模型。非线性回归模型的形式可以是多项式函数、指数函数、对数函数、三角函数等任意形式的非线性函数,这些函数可以包含自变量的高次项、交互项或其他非线性变换。常见的非线性方程如: y = x 2 {\rm{y}} = {x^2} y=x2,但是观测到的数据往往是带有噪声,于是给现有的模型一个因子 ε \varepsilon ε,并假设该因子符合标准正态分布: y = x 2 + ε {\rm{y}} = {x^2} + \varepsilon y=x2+ε。深度学习模型通常由多个神经网络层组成,每一层都包含许多神经元。每个神经元接收来自前一层的输入,并通过激活函数对输入进行非线性转换,然后将结果传递给下一层,通过多个层的堆叠,深度学习模型可以学习到多个抽象层次的特征表示。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt# 生成200个数据点,从“-0.5~0.5”均匀排布
x_data = np.linspace(-0.5, 0.5, 200)# 提升维度(200)-->(200,1)
x_data = x_data[:, np.newaxis]# 制作噪声,shape与x_data一致
noise = np.random.normal(0, 0.02, x_data.shape)# 构造目标公式
y_data = np.square(x_data) + noise# 输入层:placeholder用于接收训练的数据
x = tf.placeholder(tf.float32, [None, 1], name="x_input")
y = tf.placeholder(tf.float32, [None, 1], name="y_input")# 隐藏层
W_1 = tf.Variable(tf.random_normal([1, 10]))
b_1 = tf.Variable(tf.zeros([1, 10]))
a_1 = tf.matmul(x, W_1) + b_1
out_1 = tf.nn.tanh(a_1)# 输出层
W_2 = tf.Variable(tf.random_normal([10, 1]))
b_2 = tf.Variable(tf.zeros([1, 1]))
a_2 = tf.matmul(out_1, W_2) + b_2
out_2 = tf.nn.tanh(a_2)# 构建损失函数
loss = 1/2*tf.reduce_mean(tf.square(out_2- y))# 定义优化器
optim = tf.train.GradientDescentOptimizer(0.1)# 最小化损失函数
train_step = optim.minimize(loss)# 初始化全部的变量
init = tf.global_variables_initializer()# 训练
with tf.Session() as sess:sess.run(init)for epc in range(10000):sess.run([loss, train_step], {x:x_data,y:y_data})if epc % 1000 == 0:loss_value = sess.run([loss], {x:x_data,y:y_data})print("epc={}, loss={}".format(epc, loss_value))prediction_value = sess.run(out_2, feed_dict={x:x_data})plt.figure()
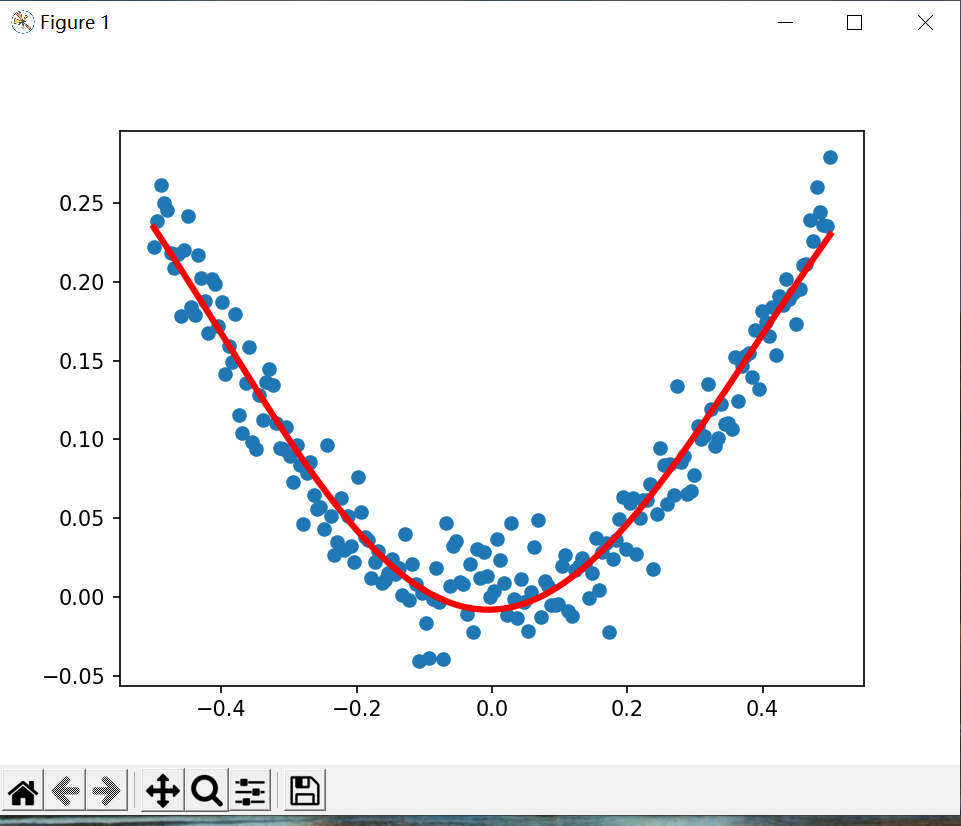
plt.scatter(x_data, y_data)
plt.plot(x_data, prediction_value, "r-", lw=3)
plt.show()
逻辑回归
逻辑回归是一种用于分类问题的统计模型,它假设目标变量与特征之间存在概率关系。逻辑回归模型通过线性函数和逻辑函数的组合来建模概率,以预测样本属于某个类别的概率。逻辑回归本身是一个简单的线性分类模型,但深度学习可以自动地学习特征表示,并通过多层非线性变换来模拟更复杂的关系。MNIST数据集通常被认为是深度学习的入门级别任务之一,可以帮助初学者熟悉深度学习的基本概念、模型构建和训练过程。虽然MNIST是一个入门级别的任务,但它并不能完全代表实际应用中的复杂视觉问题。在实践中,还需要面对更大规模的数据集、多类别分类、图像分割、目标检测等更具挑战性的问题。
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt# 载入数据集:首次调用时自动下载数据集(MNIS 数据集)并将其保存到指定的目录中。
mnist = input_data.read_data_sets("MNIST", one_hot=True)# 设置batch_size的大小
batch_size = 50
# (几乎)所有数据集被用于训练所需的次数
n_batchs = mnist.train.num_examples // batch_size# 输入层:placeholder用于接收训练的数据
# 这里图像大小是28×28,对数据集进行压缩28×28=782
x = tf.placeholder(tf.float32, [None, 784],name="x-input")
# 10分类(数字0~9)
y = tf.placeholder(tf.float32, [None, 10], name="y-input")# 隐藏层
w = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([1,10]))
# 全连接层
prediction = tf.matmul(x, w) + b
prediction_softmax = tf.nn.softmax(prediction)
# 交叉熵损失函数+计算张量在指定维度(默认0维)上的平均值
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=prediction, labels=y))# 定义优化器
optim = tf.train.GradientDescentOptimizer(0.01)# 最小化损失函数
train_step = optim.minimize(loss)# 初始化全部的变量
init = tf.global_variables_initializer()# 计算准确率:选择概率最大的数字作为预测值与真实值进行比较,统计正确的个数再计算准确率
correct_prediction = tf.equal(tf.argmax(prediction_softmax, 1), tf.argmax(y, 1))
accuarcy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))# GPU使用和显存分配:最大限度为1/3
gpu_options = tf.GPUOptions(per_process_gpu_memory_fraction=0.333)
# 用于配置 GPU
sess = tf.Session(config=tf.ConfigProto(gpu_options=gpu_options))epoch_arr = np.array([])
acc_arr = np.array([])
loss_arr = np.array([])with tf.Session() as sess:sess.run(init)# 训练总次数for epoch in range(200):# 每轮训练的迭代次数for batch in range(n_batchs):batch_x, batch_y = mnist.train.next_batch(batch_size)sess.run([train_step],{x:batch_x, y: batch_y})# 用训练集每完成一次训练,则用测试集验证acc, los = sess.run([accuarcy, loss], feed_dict = {x:mnist.test.images, y:mnist.test.labels})epoch_arr= np.append(epoch_arr, epoch)acc_arr = np.append(acc_arr, acc)loss_arr = np.append(loss_arr, los)print("epoch: ", epoch, "acc: ",acc, "loss: ", los)# 分别显示精度上升趋势和损失下降趋势
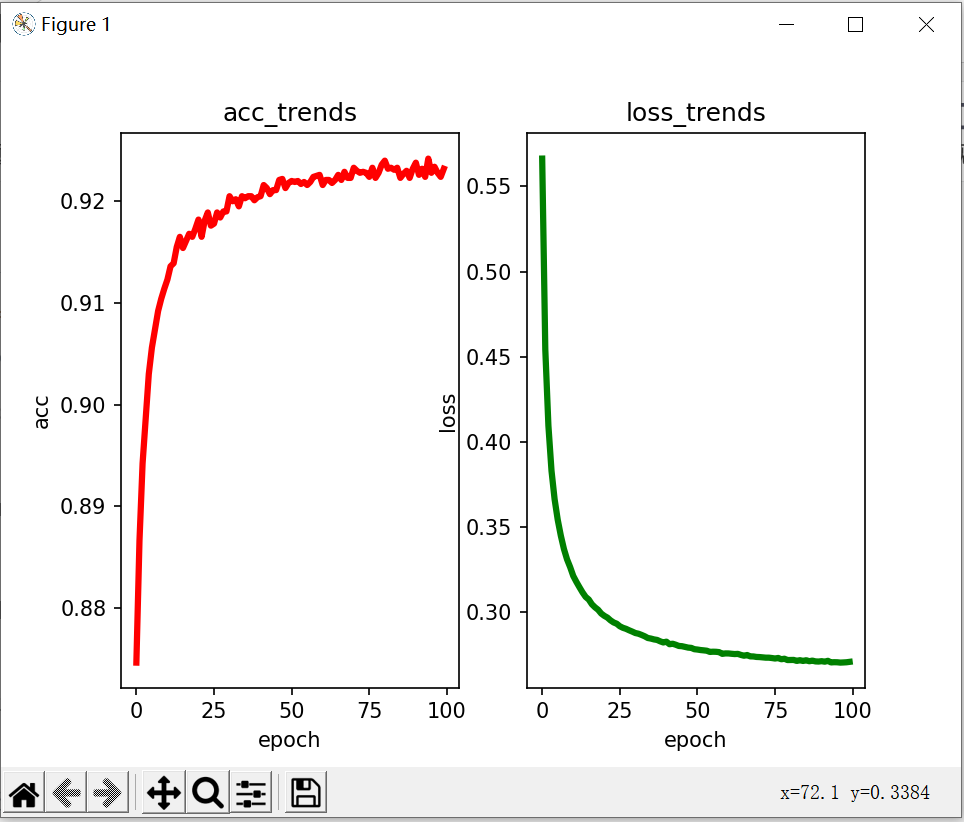
fig, (ax1, ax2) = plt.subplots(1, 2)ax1.set_title('acc_trends')
ax1.set_xlabel('epoch')
ax1.set_ylabel('acc')
ax1.plot(epoch_arr, acc_arr, "r-", lw=3)ax2.set_title('loss_trends')
ax2.set_xlabel('epoch')
ax2.set_ylabel('loss')
ax2.plot(epoch_arr, loss_arr, "g-", lw=3)
plt.show()
总结
训练深度学习模型通常需要大量的标记数据和计算资源。一种常用的训练算法是反向传播算法,它通过最小化损失函数来优化模型参数。常见的损失函数是均方误差损失函数和交叉熵损失函数,可以度量模型输出的概率分布与实际标签之间的差异。在实际应用中,深度学习通常用于处理非线性回归,而逻辑回归和线性回归则是其中的一些特殊情况。
相关文章:

【TensorFlow1.X】系列学习笔记【基础一】
【TensorFlow1.X】系列学习笔记【基础一】 大量经典论文的算法均采用 TF 1.x 实现, 为了阅读方便, 同时加深对实现细节的理解, 需要 TF 1.x 的知识 文章目录 【TensorFlow1.X】系列学习笔记【基础一】前言线性回归非线性回归逻辑回归总结 前言 本篇博主将用最简洁的代码由浅入…...

Linux 基础操作手记三(内存篇)
Linux 基础操作手记三 释放内存虚拟机彻底无网络测试网速设置虚拟内存交换空间未使用虚拟机设置虚拟内存无法开机问题GParted - 分配内存系统盘扩容自己 释放内存 sync && echo 3 > /proc/sys/vm/drop_caches 虚拟机彻底无网络 还原默认设置,静静的等待…...

NodeJS的初使用,以及引入第三方插件和安装淘宝镜像的教程
NodeJs 命令 npm init -y 生成package.json文件npm i jquery --save–dev 开发依赖(jQuery后面还可以跟模块,可以有多个)npm i jquery --save 生产依赖npm i jquery --D 开发依赖npm uninstall jquery 卸载删除npm i 把删掉的模块,全部重新加载回来 1.介绍 1.什么是NodeJs?…...

Java读取文件的N种方法
1.概述 在这篇文章里, 我们将探索不同的方式从文件中读取数据。 首先, 学习通过标准的的Java类,从classpath、URL或者Jar中加载文件。 然后,学习通用BufferedReader, Scanner, StreamTokenizer, DataInputStream, SequenceInput…...

子类的构造与析构过程
一、简介 父类,也称基类,其构造方法和析构方法不能被继承; 子类,也称派生类,继承父类的方法和属性,但要加入新的构造和析构函数。 二、构造与析构过程 构造:先调用父类——>再调用子类 析构&…...

位运算相关笔记
位运算 Part 1:基础 左移:左移一位,相当于某数乘以 2 2 2。左移 x x x位,相当于该数乘以 2 x 2^x 2x。 右移:右移一位,相当于某数除以 2 2 2。右移 x x x位,相当于该数除以 2 x 2^x 2x。 与运算&…...
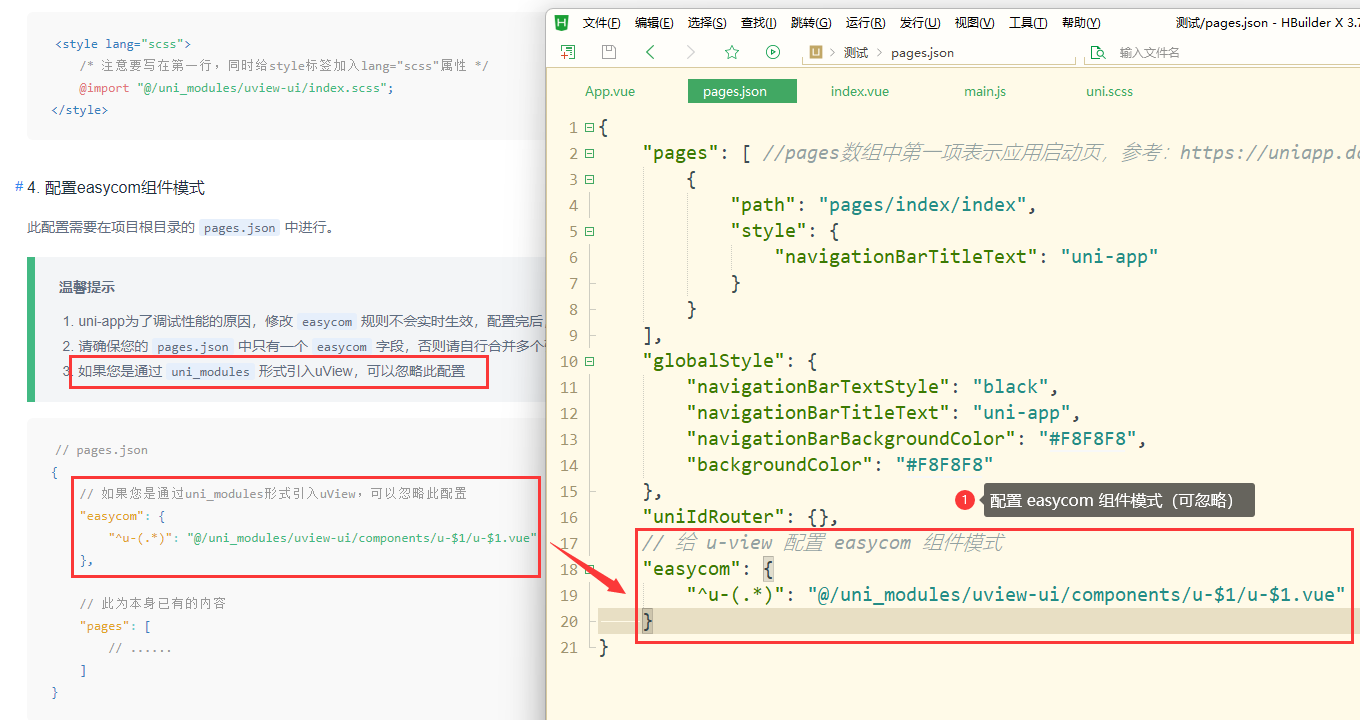
uniapp 安装 u-view 组件库
u-view 组件库安装教程:https://uviewui.com/components/install.html 注:以下使用 HBuilderx 安装 u-view 2.0 版本,不适用于其它版本。 1.安装 u-view 组件库 2、注册并登录 HBuilderx 账号,点击下载 u-view 组件库。 3、点击…...

Go 语言的成功案例:谁在使用 Go?
Go 语言,也被称为 Golang,是一门由Google开发的开源编程语言。自从2009年首次亮相以来,它在编程社区中崭露头角,并吸引了越来越多的开发者和组织。Go 以其高效的并发性、出色的性能和简单易懂的语法而闻名。在本文中,我…...

UG\NX二次开发 实时查看 NX 日志文件
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,里海BlockUI专栏,C\C++-CSDN博客 感谢粉丝订阅 感谢 a18037198459 订阅本专栏,非常感谢。 简介 实时查看 NX 日志文件,有助于分析保存时间等。打开WindowsPowerShell并实时获取日志文件内容的小功能。 效果 代…...

ZooKeeper+HBase分布式集群环境搭建
安装版本:hadoop-2.10.1、zookeeper-3.4.12、hbase-2.3.1 一、zookeeper集群搭建与配置 1.下载zookeeper安装包 2.解压移动zookeeper 3.修改配置文件(创建文件夹) 4.进入conf/ 5.修改zoo.cfg文件 6.进入/usr/local/zookeeper-3.4.12/zkdata…...
喜讯!持安科技入选2023年北京市知识产权试点单位!
近日,北京市知识产权局发布了“2023年度北京市知识产权试点示范单位及2020年度北京市知识产权试点示范单位复审通过名单”名单。 经过严格的初审、形式审核和专家评审,北京持安科技有限公司入选“2023年北京市知识产权试点单位”。 北京市知识产权试点示…...
)
笙默考试管理系统-MyExamTest----codemirror(39)
笙默考试管理系统-MyExamTest----codemirror(39) 目录 一、 笙默考试管理系统-MyExamTest 二、 笙默考试管理系统-MyExamTest 三、 笙默考试管理系统-MyExamTest 四、 笙默考试管理系统-MyExamTest 五、 笙默考试管理系统-MyExamTest 笙默考试…...
抛砖引玉:Redis 与 接口自动化测试框架的结合
接口自动化测试已成为保证软件质量和稳定性的重要手段。而Redis作为一个高性能的缓存数据库,具备快速读写、多种数据结构等特点,为接口自动化测试提供了强大的支持。勇哥这里粗略介绍如何结合Python操作Redis,并将其应用于接口自动化测试框架…...

网站如何才能不被黑,如何做好网络安全
当企业网站受到攻击时,首页文件可能被篡改,百度快照也可能被劫持并重定向到其他网站。首要任务是加强网站的安全防护。然而,许多企业缺乏建立完善的网站安全防护体系的知识。因此,需要专业的网站安全公司来提供相应的保护措施。今…...

人脸写真FaceChain风格写真的试玩(二)
接着上一篇【人脸写真FaceChain的简单部署记录(一)】来试玩一下。 1 无限风格写真 参考:让你拥有专属且万能的AI摄影师AI修图师——FaceChain迎来最大版本更新 1.1 人物形象训练 这里的步骤比较简单,就是选择照片,然…...
PHP 变量
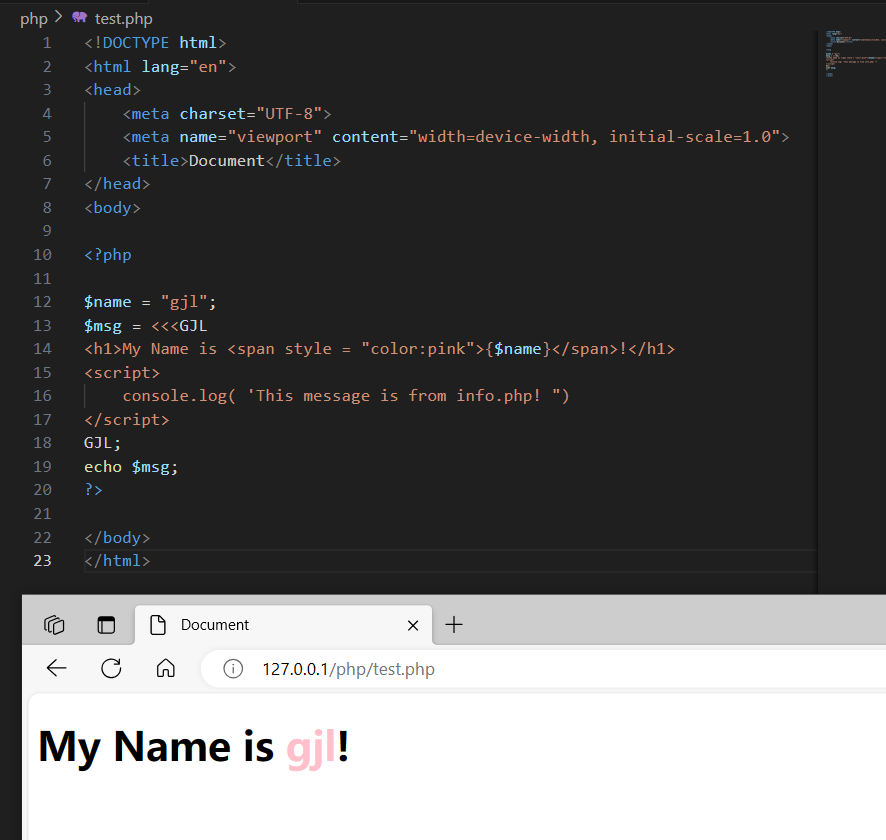
变量 变量的声明、使用、释放 变量定义 形式 $ 变量名;严格区分大小写 $name; $Name; $NAME //三个变量不是同一个变量字母、数字、下划线组成,不能以数字开头,不能包含其他字符(空白字符、特殊字符) 驼峰式命名法、下划线式命名法 $first_name; $fi…...

牛客小白月赛79
给定一个数字n,你可以对它进行接下来的操作—— 选择数字中任意一个数位删除 例如对1024选择操作百位,数字则变成了124;对1024选择操作千位,数字则变成了024 我们称一个数字是干净的,当且仅当数字满足以下任意一种…...
面试算法31:最近最少使用缓存
题目 请设计实现一个最近最少使用(Least Recently Used,LRU)缓存,要求如下两个操作的时间复杂度都是O(1)。 get(key):如果缓存中存在键key,则返回它对应的值…...

如何处理前端SEO(搜索引擎优化)?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...
Leetcode—2529.正整数和负整数的最大计数【简单】
2023每日刷题(四) Leetcode—2529.正整数和负整数的最大计数 遍历法实现代码 int maximumCount(int* nums, int numsSize){int i;int neg 0, pos 0;for(i 0; i < numsSize; i) {if(nums[i] < 0) {neg;}if(nums[i] > 0) {pos;}}return (neg…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
