位运算相关笔记
位运算
Part 1:基础
-
左移:左移一位,相当于某数乘以 2 2 2。左移 x x x位,相当于该数乘以 2 x 2^x 2x。
-
右移:右移一位,相当于某数除以 2 2 2。右移 x x x位,相当于该数除以 2 x 2^x 2x。
-
与运算:按位进行“与”运算,两数同一位都为 1 1 1 时结果为 1 1 1,否则为 0 0 0。 0 0 0 与任何数都为 0 0 0。
-
或运算:按位进行“或”运算,两数同一位都为 0 0 0 时结果为 0 0 0,否则为 1 1 1。
-
非运算:按位取反。
Part 2:异或
简介
异或操作,是指两个数或者多个数之间进行的一种相同为 0 0 0、不同为 1 1 1的位运算。
异或操作通常用 ⊕ \oplus ⊕或^表示。
运算律
-
0 ⊕ n = n 0\oplus n=n 0⊕n=n, n ⊕ n = 0 n\oplus n=0 n⊕n=0
-
结合律
-
交换律:一堆数在一起进行异或操作时,可以按任意顺序进行。
应用
-
交换两个数:
a=a^b,b=a^b,a=a^b; -
找到某个数
一个数组中只有一个数出现了奇数次,其余数都出现了偶数次,如何找到这个出现奇数次的数?
根据异或运算的性质,一个数与自己异或等于零,一个数与 0 0 0异或等于本身可知,只需将数组中的所有数进行异或操作即可将出现偶数次的数消掉,得到出现奇数次的。
-
i ⊕ 1 i\oplus 1 i⊕1 表示 i i i 的反向边。
证明:对于一个数 n n n,如果它是奇数,那么它异或 1 1 1 等于 n − 1 n-1 n−1;如果它是偶数,那么它异或 1 1 1 等于 n + 1 n+1 n+1。
对于 Tarjan 求边双连通分量,有一段标记是
isb[i]=isb[i^1]=1(标记该边和它的反向边是桥 bridge),插入的时候是成对插入的( ( 0 , 1 ) 、 ( 1 , 2 ) 、 ⋯ 、 ( 2 k , 2 k + 1 ) (0,1)、(1,2)、\cdots、(2k,2k+1) (0,1)、(1,2)、⋯、(2k,2k+1))。
Part 3:lowbit
定义
lowbit ( n ) \text{lowbit}(n) lowbit(n) 定义为非负整数 n n n在二进制表示下“最低位的 1 1 1及其后面的所有 0 0 0”构成的数值。
举个栗子, n = 10 n=10 n=10 的二进制表示为 ( 1010 ) 2 (1010)_2 (1010)2,则 lowbit ( n ) = 2 = ( 10 ) 2 \text{lowbit}(n)=2=(10)_2 lowbit(n)=2=(10)2。
公式
lowbit ( n ) = n & ( ∼ n + 1 ) = n & ( − n ) \text{lowbit}(n)=n\&(\sim n+1)=n\&(-n) lowbit(n)=n&(∼n+1)=n&(−n)
应用
lowbit \text{lowbit} lowbit运算配合Hash,可以找出整数二进制表示下所有是 1 1 1的位,时间复杂度与 1 1 1的个数同级。
实现:不断把 n n n 赋值为 n − lowbit ( n ) n-\text{lowbit}(n) n−lowbit(n),直至 n = 0 n=0 n=0。
举个栗子: n = 9 = ( 1001 ) 2 n=9=(1001)_2 n=9=(1001)2, lowbit ( 9 ) = 1 \text{lowbit}(9)=1 lowbit(9)=1。把 n n n 赋值为 9 − lowbit ( n ) = 8 = ( 1000 ) 2 9-\text{lowbit}(n)=8=(1000)_2 9−lowbit(n)=8=(1000)2。 8 − lowbit ( 8 ) = 0 8-\text{lowbit}(8)=0 8−lowbit(8)=0,停止循环。在这个过程中减掉了 1 1 1 和 8 8 8,即 n n n 每一位上的 1 1 1 后补 0 0 0 后的数值。取 log 2 1 \log_21 log21 和 log 2 8 \log_28 log28,就可以知道 n n n 的第 1 1 1 位和第 3 3 3 位是 1 1 1。
C++中的 log2 函数效率不够高,所以我们要预处理一个数组,用 Hash 代替 log \log log 运算。
当 n n n较小时,可以建立一个数组 h,令 h [ 2 k ] = k h[2^k]=k h[2k]=k。
const int maxn=1<<20;
int h[maxn+5];
for(int i=1;i<=20;i++) h[1<<i]=i;
while(cin>>n)
{while(n>0) cout<<h[n&-n]<<' ',n-=n&-n;cout<<endl;
}
还有一种方法,建立一个长度为 37 37 37 的数组 h,令 h [ 2 k m o d 37 ] = k h[2^k\bmod 37]=k h[2kmod37]=k( ∀ k ∈ [ 0 , 35 ] \forall k\in[0,35] ∀k∈[0,35], 2 k m o d 37 2^k\bmod 37 2kmod37 互不相等,可以取遍 1 ∼ 36 1\sim36 1∼36)。
int h[37];
for(int i=0;i<36;i++) h[(1ll<<i)%37]=i;
while(cin>>n)
{while(n>0) cout<<h[(n&-n)%37]<<' ',n-=n&-n;cout<<endl;
}
lowbit 运算还可用于树状数组。
更多函数
-
int __builtin_ctz(unsigned int x)int __builtin_ctzll(unsigned long long x)返回 x x x 的二进制表示下最低位的 1 1 1 后边有多少个 0 0 0。
-
int __builtin_popcount(unsigned int x)int __builtin_popcountll(unsigned long long x)返回 x x x 的二进制表示下有多少位为 1 1 1。
常见操作
-
查询一个数二进制下的第 i i i 为是不是 1 1 1:
x>>i&1,如果第 i i i 位是 1 1 1 这个值是 1 1 1,否则是 0 0 0。常见用途: 01 01 01 字典树、线性基
-
枚举子集
常用于状压。
for(int S1=S;S1;S1=(S1-1)&S) S2=S^S1;其中 S S S 是全集, S 1 S_1 S1 是子集, S 2 S_2 S2 是 S 1 S_1 S1 的补集。
-
改变 x x x 的第 i i i 位
x|=1<<(i-1);//将x第i位变成1 x&=~(1<<(i-1));//将x第i位变成0 -
查询 1 1 1 的个数
int popcount(int n) {int cnt=0;while(n) n&=(n-1),cnt++;return cnt; }
相关文章:

位运算相关笔记
位运算 Part 1:基础 左移:左移一位,相当于某数乘以 2 2 2。左移 x x x位,相当于该数乘以 2 x 2^x 2x。 右移:右移一位,相当于某数除以 2 2 2。右移 x x x位,相当于该数除以 2 x 2^x 2x。 与运算&…...
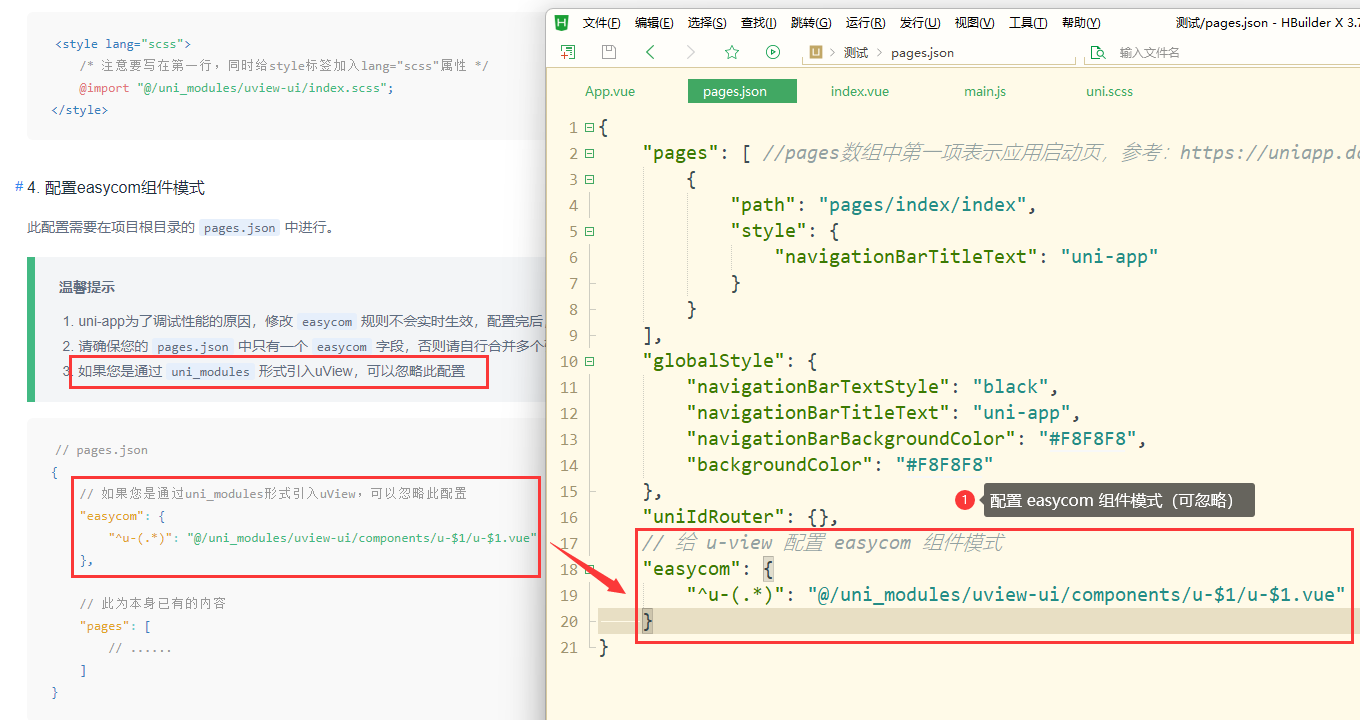
uniapp 安装 u-view 组件库
u-view 组件库安装教程:https://uviewui.com/components/install.html 注:以下使用 HBuilderx 安装 u-view 2.0 版本,不适用于其它版本。 1.安装 u-view 组件库 2、注册并登录 HBuilderx 账号,点击下载 u-view 组件库。 3、点击…...

Go 语言的成功案例:谁在使用 Go?
Go 语言,也被称为 Golang,是一门由Google开发的开源编程语言。自从2009年首次亮相以来,它在编程社区中崭露头角,并吸引了越来越多的开发者和组织。Go 以其高效的并发性、出色的性能和简单易懂的语法而闻名。在本文中,我…...

UG\NX二次开发 实时查看 NX 日志文件
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,里海BlockUI专栏,C\C++-CSDN博客 感谢粉丝订阅 感谢 a18037198459 订阅本专栏,非常感谢。 简介 实时查看 NX 日志文件,有助于分析保存时间等。打开WindowsPowerShell并实时获取日志文件内容的小功能。 效果 代…...

ZooKeeper+HBase分布式集群环境搭建
安装版本:hadoop-2.10.1、zookeeper-3.4.12、hbase-2.3.1 一、zookeeper集群搭建与配置 1.下载zookeeper安装包 2.解压移动zookeeper 3.修改配置文件(创建文件夹) 4.进入conf/ 5.修改zoo.cfg文件 6.进入/usr/local/zookeeper-3.4.12/zkdata…...
喜讯!持安科技入选2023年北京市知识产权试点单位!
近日,北京市知识产权局发布了“2023年度北京市知识产权试点示范单位及2020年度北京市知识产权试点示范单位复审通过名单”名单。 经过严格的初审、形式审核和专家评审,北京持安科技有限公司入选“2023年北京市知识产权试点单位”。 北京市知识产权试点示…...
)
笙默考试管理系统-MyExamTest----codemirror(39)
笙默考试管理系统-MyExamTest----codemirror(39) 目录 一、 笙默考试管理系统-MyExamTest 二、 笙默考试管理系统-MyExamTest 三、 笙默考试管理系统-MyExamTest 四、 笙默考试管理系统-MyExamTest 五、 笙默考试管理系统-MyExamTest 笙默考试…...
抛砖引玉:Redis 与 接口自动化测试框架的结合
接口自动化测试已成为保证软件质量和稳定性的重要手段。而Redis作为一个高性能的缓存数据库,具备快速读写、多种数据结构等特点,为接口自动化测试提供了强大的支持。勇哥这里粗略介绍如何结合Python操作Redis,并将其应用于接口自动化测试框架…...

网站如何才能不被黑,如何做好网络安全
当企业网站受到攻击时,首页文件可能被篡改,百度快照也可能被劫持并重定向到其他网站。首要任务是加强网站的安全防护。然而,许多企业缺乏建立完善的网站安全防护体系的知识。因此,需要专业的网站安全公司来提供相应的保护措施。今…...

人脸写真FaceChain风格写真的试玩(二)
接着上一篇【人脸写真FaceChain的简单部署记录(一)】来试玩一下。 1 无限风格写真 参考:让你拥有专属且万能的AI摄影师AI修图师——FaceChain迎来最大版本更新 1.1 人物形象训练 这里的步骤比较简单,就是选择照片,然…...
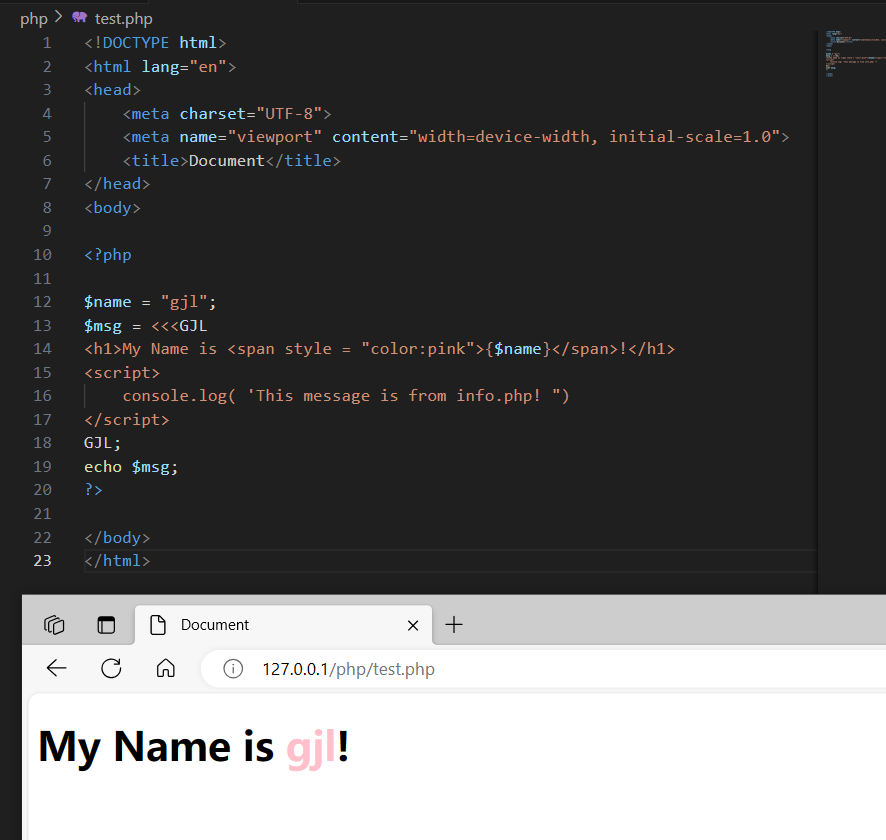
PHP 变量
变量 变量的声明、使用、释放 变量定义 形式 $ 变量名;严格区分大小写 $name; $Name; $NAME //三个变量不是同一个变量字母、数字、下划线组成,不能以数字开头,不能包含其他字符(空白字符、特殊字符) 驼峰式命名法、下划线式命名法 $first_name; $fi…...

牛客小白月赛79
给定一个数字n,你可以对它进行接下来的操作—— 选择数字中任意一个数位删除 例如对1024选择操作百位,数字则变成了124;对1024选择操作千位,数字则变成了024 我们称一个数字是干净的,当且仅当数字满足以下任意一种…...
面试算法31:最近最少使用缓存
题目 请设计实现一个最近最少使用(Least Recently Used,LRU)缓存,要求如下两个操作的时间复杂度都是O(1)。 get(key):如果缓存中存在键key,则返回它对应的值…...

如何处理前端SEO(搜索引擎优化)?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...
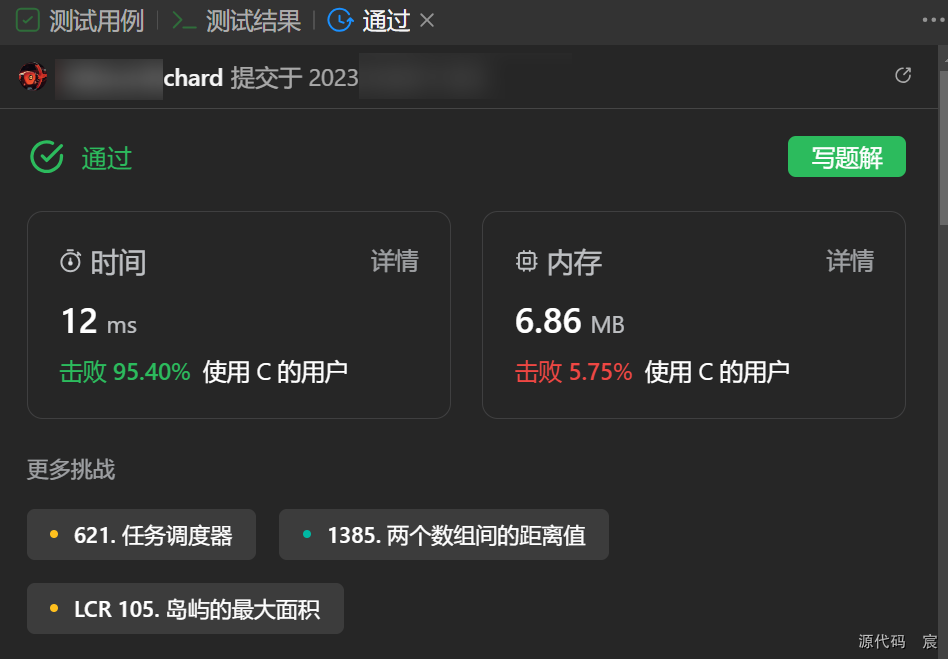
Leetcode—2529.正整数和负整数的最大计数【简单】
2023每日刷题(四) Leetcode—2529.正整数和负整数的最大计数 遍历法实现代码 int maximumCount(int* nums, int numsSize){int i;int neg 0, pos 0;for(i 0; i < numsSize; i) {if(nums[i] < 0) {neg;}if(nums[i] > 0) {pos;}}return (neg…...

数据结构-- 并查集
0. 引入 并查集是来解决等价问题的数据结构。 离散数学中的二元关系。 等价关系需满足自反性、对称性、传递性。 a ∈ S , a R a a R b & b R a a R b ∩ b R c > a R c a \in S, aRa \\ aRb \& bRa \\ aRb \cap bRc >aRc a∈S,aRaaRb&bRaaRb∩bRc>a…...
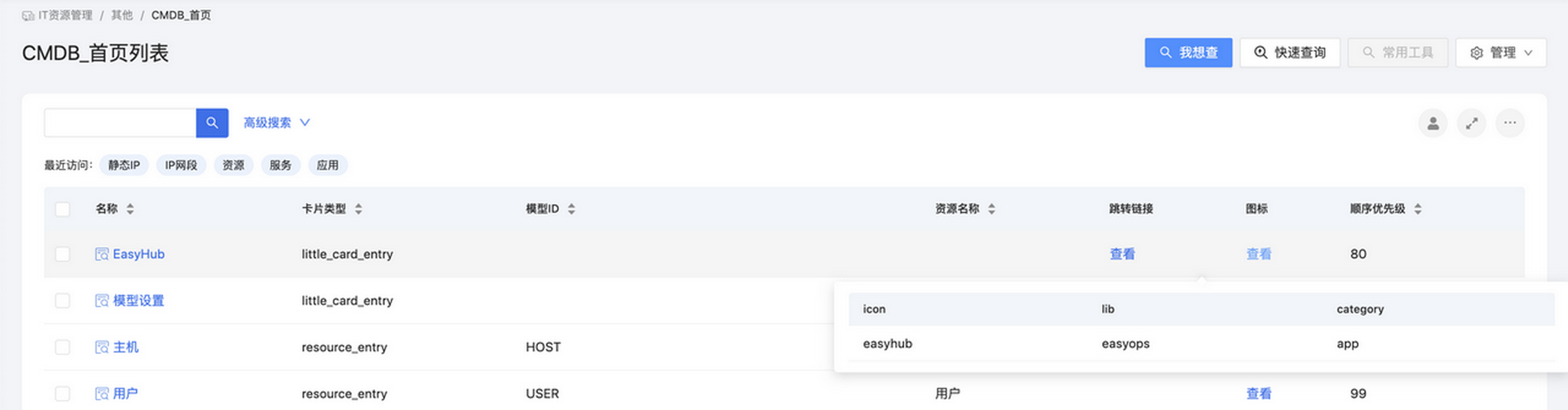
优维产品最佳实践第12期:IT资源管理首页丰富
背 景 当我们进入平台后,默认跳转至IT资源管理首页,因此该页面的优化与丰富将极大的提高平台使用者的体验和效率。优化后的首页可以更好地展示常用模型、小产品、外部系统、以及保存的所有关系查询和快速查询条件,使用户能够更快捷、方便…...
【Nginx34】Nginx学习:安全链接、范围分片以及请求分流模块
Nginx学习:安全链接、范围分片以及请求分流模块 又迎来新的模块了,今天的内容不多,但我们都进行了详细的测试,所以可能看起来会多一点哦。这三个模块之前也从来都没用过,但是通过学习之后发现,貌似还都挺有…...

PO模式在selenium自动化测试框架的优势
大家都知道po模式可以提高代码的可读性和减少了代码的重复,但是相对的缺点还有,今天通过本文一起学习下PO模式在selenium自动化测试框架的优势,需要的朋友可以参考下 PO模式简介 1.什么是PO模式 PO模型是:Page Object Model的简写 页面对象…...
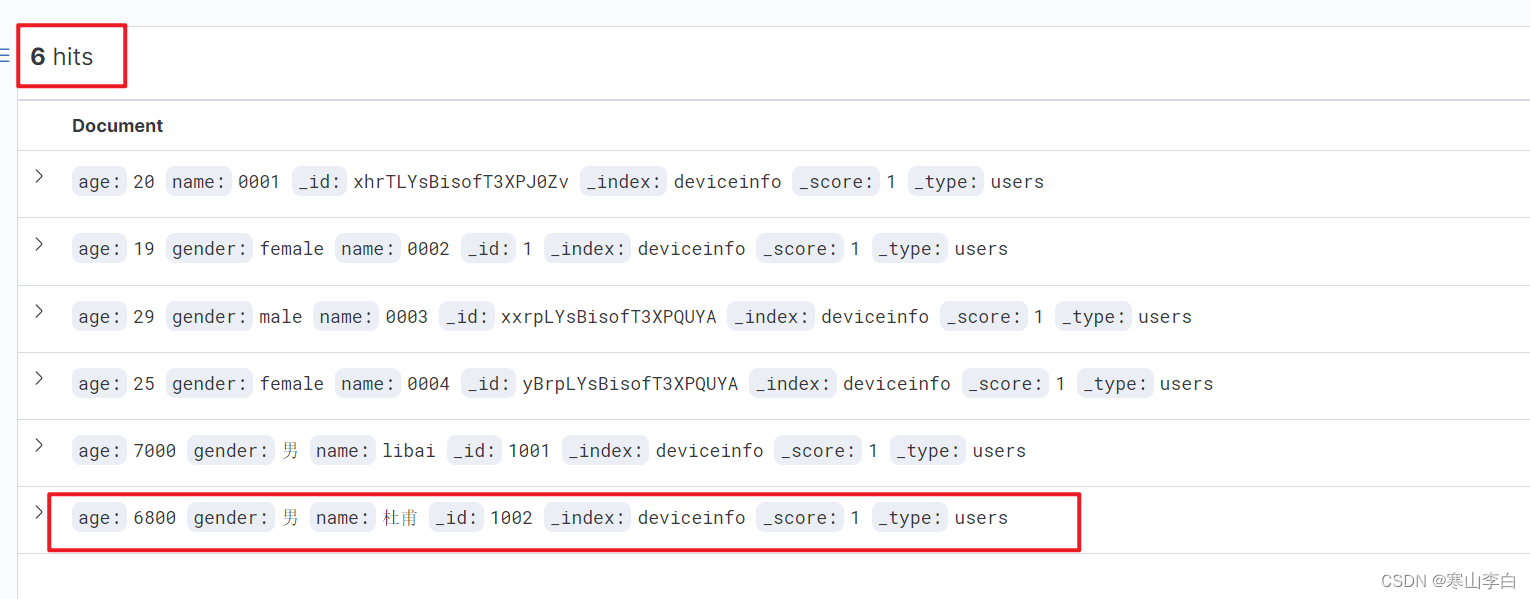
Java操作Elasticsearch(新增数据)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
