第十二届蓝桥杯模拟赛第一期
A填空题
问题描述
如果整数a是整数b的整数倍,则称b是a的约数。
请问,有多少个正整数是2020的约数。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
参考答案
12
public class Main {public static void main(String[] args) {int ans=0;for(int i=1;i<=2020;i++) {if(2020%i==0) {ans++;}}System.out.println(ans);}
}B填空题
问题描述
如果一个mp3文件占用磁盘的大小是4MB,小蓝的硬盘还剩下100GB的空间,请问他还可以放多少个这样的mp3文件?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
参考答案
25600
//1GB=1024MB
1MB = 1024KB
1KB = 1024字节(byte)
1字节 = 8位(bits)
public class Main {public static void main(String[] args) {int ans=100*1024/4;System.out.println(ans);}
}
C填空题
问题描述
一个包含2020个结点的无向图,如果图中没有自环和重边,最多包含多少条边?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
参考答案
2039190
public class Main {public static void main(String[] args) {int ans=2020*(2020-1)/2;System.out.println(ans);}
}
D填空题
问题描述
整数1到6连在一起,成为123456,长度为6。
整数1到12连在一起,成为123456789101112,长度为15。
请问整数1到2020连在一起,长度为多少?
答案提交
这是一道结果天空的题,你只需要算出结果后提交即可。本题的结果为个整数,在提交答案时只垍写这个整数,垍写
多余的内容将无法得分。
参考答案
6973
public class Main {public static void main(String[] args) {String str="";for(int i=1;i<=2020;i++) {str=str+i;}System.out.println(str.length());}
}E填空题
问题描述
在一个序列a = (a[1], a[2], …, a[n]) 中,如果(i, j)满足 i < j 且 a[i] > a[j],则称为一个逆序对。
例如:(3, 2, 2, 1) 中包含6个逆序对。
请问,(87, 39, 35, 1, 99, 10, 54, 1, 46, 24, 74, 62, 49, 13, 2, 80, 24, 58, 8, 14, 83, 23, 97, 85, 3, 2, 86, 10, 71, 15) 中包含多少个逆序对?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
结果
217
//题目给的例题好像错了,是5对
public class Main {public static void main(String[] args) {int ans=0;int[] a=new int[] {87, 39, 35, 1, 99, 10, 54, 1, 46, 24, 74, 62, 49, 13, 2, 80, 24, 58, 8, 14, 83, 23, 97, 85, 3, 2, 86, 10, 71, 15};for(int i=0;i<=a.length-1;i++) {for(int j=0;j<=a.length-1;j++) {if(i<j&&a[i]>a[j]) {ans++;}}}System.out.println(ans);}
}相关文章:

第十二届蓝桥杯模拟赛第一期
A填空题 问题描述 如果整数a是整数b的整数倍,则称b是a的约数。 请问,有多少个正整数是2020的约数。 答案提交 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数࿰…...

【生成对抗网络】
生成对抗网络(Generative Adversarial Networks,简称GANs)是深度学习领域的一种创新结构,由Ian Goodfellow在2014年首次提出。GANs包括两个深度神经网络——一个生成器和一个判别器,它们通常以对抗的方式进行训练。 以…...

Redis性能滑坡:哈希表碰撞的不速之客【redis第二部分】
Redis性能滑坡:哈希表碰撞的不速之客 前言第一部分:Redis哈希表简介第二部分:哈希表冲突原因第三部分:Redis哈希函数第四部分:哈希表冲突的性能影响第五部分:解决冲突策略第六部分:redis是如何解…...

科技与教育的盛宴——探讨监控易在82届教装展的新机遇
在第82届中国教育装备展示会这个融合了科技与教育的盛宴上,监控易将展现其最新的教育信息化解决方案和技术创新成果。这不仅是一次产品的展示,更是一次理念、技术与需求的交流和碰撞。在这里,我们将一同探讨在科技日新月异的今天,…...
Bazzite:专为 Steam Deck 和 PC 上的 Linux 游戏打造的发行版
导读对于一个专为 Linux 游戏定制的发行版,你是否感兴趣呢?如果答案是肯定的,那么我们为你准备了绝佳选择。 Bazzite 是一个新推出的基于 Fedora 的发行版,它是为 Linux 桌面上的游戏,以及越来越火热的 Steam Deck 定…...

【MySQL】数据库数据类型
文章目录 1. 整体概要2. 数值类型(有符号) tinyint 创建表(无符号) tinyint 创建表bit类型float 类型(无符号)floatdecimal 3. 二进制类型char类型varchar类型 4. 日期时间日期时间类型 5. string 类型enum类型和set类型enum类型和set类型的查找在枚举中的查找在set中的查找 1.…...

计算机组成原理 new07 真值和机器数 无符号整数 定点整数 定点小数 $\color{red}{Δ}$
文章目录 真值和机器数 无符号整数无符号整数的定义无符号整数的特征无符号整数的表示范围无符号整数的加法无符号数的减法 有符号整数(定点整数)有符号整数的定义原码原码的特点反码反码的特点补码补码的特点快速求解n位负数补码的方法为什么补码能够多表示一个范围(重点)变形…...
基于SSM的文化培训学校网站的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

gitee-git使用
克隆gitee某代码仓库某分支流程 1.克隆远程gitee仓库某分支到本地 2.如果克隆gitee仓库是私有的系统会弹出弹框让你输入gitee的账户和密码 3.克隆远程分支完成 git所需命令 克隆远程仓库到本地 git clone 仓库URLgit克隆远程分支到本地 git clone -b 分支名 仓库URLgit 拉…...
)
欧拉图(Euler Graph)
这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系,下面给出定义: 通过图中所有边恰好一次且行遍所有顶点的通路称为 欧拉通路; 通过图中所有边恰好一次且行遍所有顶点的回路称为 欧拉回路; 具有欧拉回路的无向图称为 欧拉图; 具有欧拉通路但不具有欧拉回路的无向图…...

【安全体系架构】——零信任网络架构
什么是零信任网络架构? 零信任网络架构是一种网络和信息安全模型,它将传统的信任模型颠覆,不再信任内部或外部用户、设备或网络。相反,它将每个访问请求都视为不受信任,要求对每个用户、设备和流量都进行认证和授权&a…...

mybatis动态sql一对多查询
在数据库设计中,一对多关系是非常多的,例如消息通知和附件,一个消息通知中往往会包含多个附件,这种情况下使用mybatis动态sql可以很方便的查询出来。 1、数据库设计 消息表:sys_message CREATE TABLE sys_message (i…...
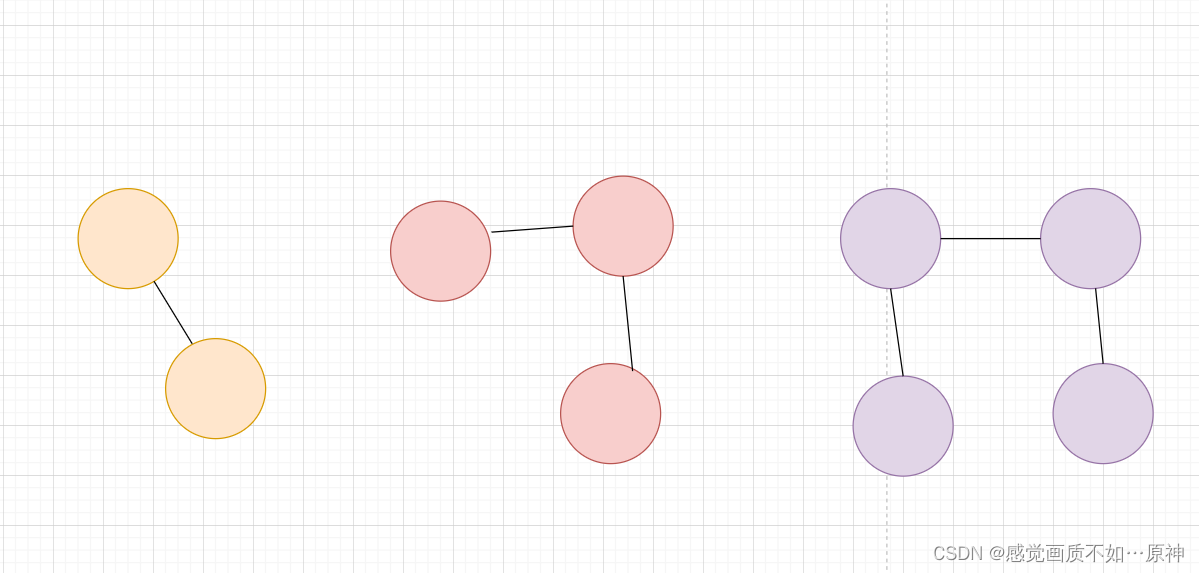
Leetcode.2316 统计无向图中无法互相到达点对数
题目链接 Leetcode.2316 统计无向图中无法互相到达点对数 rating : 1604 题目描述 给你一个整数 n n n ,表示一张 无向图 中有 n n n 个节点,编号为 0 0 0 到 n − 1 n - 1 n−1 。同时给你一个二维整数数组 e d g e s edges edges ,其…...

介绍机器学习中CatBoost工具的详细使用指南
在机器学习的动态世界中,Python 是创新背后的驱动力,专业人士必须使用正确的工具。CatBoost 就是这样一个工具,以其卓越的速度和准确性悄然改变了该领域。在本指南中,我们将深入研究 Python 3 中的 CatBoost,涵盖基础知识、高级技术和实际示例,包括使用示例数据集和绘图进…...

操作系统【OS】线程与进程的比较
进程 线程 是什么的单位? 是资源分配的基本单位 是调度的基本单位 不能共享什么? 不能共享虚拟地址空间 不能共享栈指针 可以共享什么? 拥有一个完整的资源平台 每个进程都有独立的地址空间和资源 除了共享全局变量,不允许其他进程访问 某进程中的线程…...
在Mac上使用安卓桌面模式
在安装Homeblew的基础上 替换国内源 export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" export HOMEBREW_BREW_GIT_REMOTE"https://mirrors.tuna.tsinghua.edu.cn/git/homebrew/brew.git" brew update 安装Scrcpy …...

YOLO目标检测——人脸口罩佩戴数据集【(含对应voc、coco和yolo三种格式标签】
实际项目应用:公共场所监控场景下的大密度人群检测是否佩戴口罩,以及戴口罩的人证比对(安检刷脸不用摘口罩)、手机解锁、刷脸考勤等身份认证场景。数据集说明:人脸口罩佩戴检测数据集,真实场景的高质量图片…...
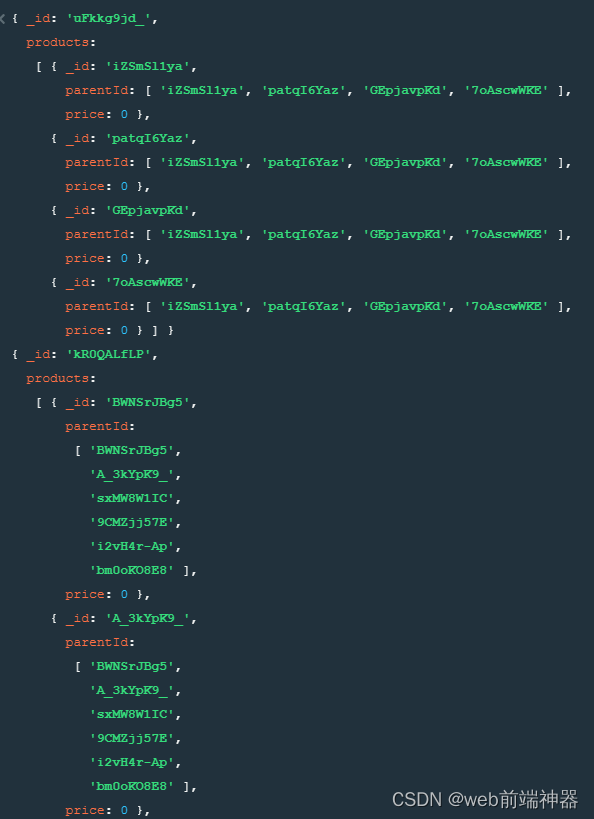
mongodb如何多表查询,如同时查询店铺以及里面对应的商品
多表查询场景介绍 一种很常见的场景,比如电商首页中,需要同时展示最近比较火热的店铺,以及直接展示店铺里对应的商品。或者用户下单之后购物车里可以看到所选的商品以及对应的店铺。如果不知道如何用mongodb自带的查询语句快速查询的话&#…...

Linux环境修改服务器时间和网络时间保持一致
目录 介绍UTC和CST 修改时区 修改时间 介绍UTC和CST UTC是协调世界时,是全球统一的时间标准。UTC的时间是基于原子钟计算的,以秒为单位,不受夏令时等影响。世界各地都可以通过UTC来同步时间。 CST是中央标准时间,相当于UTC-6…...

CUDA学习笔记6——事件计时
事件计时 CUDA事件是直接在GPU上实现的,因此它们不适用于对同时包含设备代码和主机代码的混合代码计时。 cudaEventCreate 创建一个事件cudaEventRecord 记录一个事件cudaEventElapsedTime 计算两个事件之间经历的时间,第一个参数为某个浮点变量的地址…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
