【算法教程】排列与组合的实现
数据准备
- 在讲排列与组合之前,我们先定义数据元素类型Fruit
class Fruit{constructor(name,price){this.name = namethis.price = price}
}
排列
- 对N个不同元素进行排序,总共有多少不同的排列方式?
Step1: 从N个元素中取1个,共N种取法
Step2: 从剩下N-1个元素取1个,共N-1种
......
StepN: 从剩1个元素中取1个,共1种
所以共有 A=N*(N-1)....*1 =N!
- 例子:某水果店有以下水果,请对所有水果进行全排列,请输出所有排列
let fruits = [new Fruit('apple',5.3),new Fruit('banana',3.2),new Fruit('orange',4.6),new Fruit('watermelon',2.5)
]
- 排列算法的javascript实现模板(DSF,最优解in-place)
const premutation = (elements)=>{let res = []const swap = (arr,i1,i2)=> [arr[i1],arr[i2]] = [arr[i2],arr[i1]]const dsf = (elements,k = 0)=>{let len = elements.lengthif(k == len-1){ // 如果想从N=4中,取3个的全排 只需要改这个k=3res.push([...elements.slice(0,k+1)])return}for(let i = k; i < len - 1 ; i++){swap(elements, i, k) // 从剩下[k,...,(len-2)]中 取一个 放到当前k位置dsf(elements, k + 1) // dsf继续下一个位置 [k+1,...,(len-2)]swap(elements,i , k) // 为下一个迭代(k+1)做回滚}}dsf(elements)return res
}
let premutations = premutation(fruits)
premutations.forEach((e,i)=>console.log(i,...e.map(x=>x.name)))- 测试结果
0 'apple' 'banana' 'orange' 'watermelon'
1 'apple' 'orange' 'banana' 'watermelon'
2 'banana' 'apple' 'orange' 'watermelon'
3 'banana' 'orange' 'apple' 'watermelon'
4 'orange' 'banana' 'apple' 'watermelon'
5 'orange' 'apple' 'banana' 'watermelon'
组合
- 对N个不同元素进行排序,总共有多少不同的组合方式?
N个元素中,每个元素要么被放到某个组合中,或者不放,2种选择
所以共有 C=2^N算法实现: 同样我们可以用DSF,但是还有更优解法-- 整型编码/bitmap
2^N种情况可以用N个bit来表示,通过实现对数组索引index来编码
- 同样的例子:请输出所有组合
let fruits = [new Fruit('apple',5.3),new Fruit('banana',3.2),new Fruit('orange',4.6),new Fruit('watermelon',2.5)
]
- 组合算法的javascript实现模板(bitmap)
const combination = (elements)=>{let res = []let len = elements.lengthlet counts = 1 << lenfor(let bitmap = 0 ; bitmap < counts; bitmap++){let set = []for(let i=0 ; i < len ; i++){if((1<<i)&bitmap){ //对应位为1,怎加入当前集合种set.push(i)}}// set 只是数组索引的组合,需要转成对应elementres.push(set.map(i=>elements[i])) // 完成一个集合的收集}return res
}
let combinations = combination(fruits)
combinations.forEach((e,i)=>console.log(i,...e.map(x=>x.name)))
- 测试结果
0 ''
1 'apple'
2 'banana'
3 'apple' 'banana'
4 'orange'
5 'apple' 'orange'
6 'banana' 'orange'
7 'apple' 'banana' 'orange'
8 'watermelon'
9 'apple' 'watermelon'
10 'banana' 'watermelon'
11 'apple' 'banana' 'watermelon'
12 'orange' 'watermelon'
13 'apple' 'orange' 'watermelon'
14 'banana' 'orange' 'watermelon'
15 'apple' 'banana' 'orange' 'watermelon'
相关文章:

【算法教程】排列与组合的实现
数据准备 在讲排列与组合之前,我们先定义数据元素类型Fruit class Fruit{constructor(name,price){this.name namethis.price price} }排列 对N个不同元素进行排序,总共有多少不同的排列方式? Step1: 从N个元素中取1个,共N种…...

uniapp实现简单的九宫格抽奖(附源码)
效果展示 uniapp实现大转盘抽奖 实现步骤: 1.该页面可设置8个奖品,每个奖品可设置中奖机会的权重,如下chance越大,中奖概率越高(大于0) // 示例代码 prizeList: [{id: 1,image: "https://img.alicdn…...
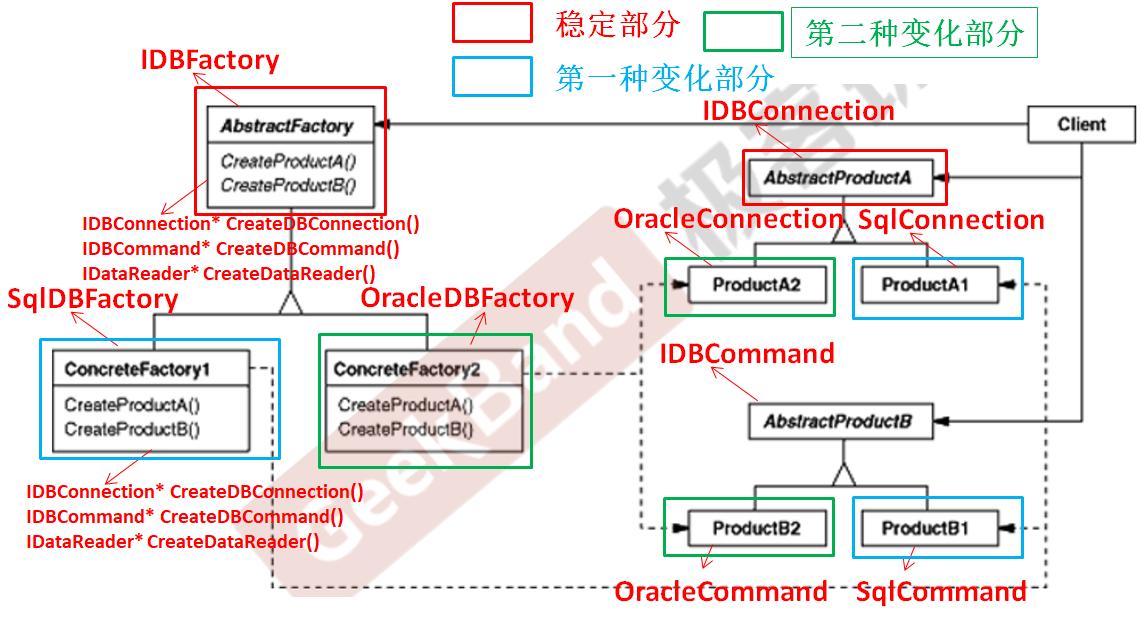
C++设计模式_09_Abstract Factory 抽象工厂
与上篇介绍的Factory Method工厂方法模式一样,Abstract Factory 抽象工厂模式也属于典型的“对象创建模式”模式,解决的问题也极其相似,在理解了Factory Method工厂方法模式的基础上再去理解Abstract Factory 抽象工厂模式就会变得更加容易。…...
一些前端面试思考
回流和重绘 先牢记这句话,回流必将引起重绘,而重绘不一定会引起回流。回流的代价要远大于重绘。 当你给一个元素更换颜色,这样的行为是不会影响页面布局的,DOM树不会变化,但颜色变了,渲染树得重新渲染页面&…...
)
Spring MVC(上)
1、Spring MVC简介: MVC是一种软件架构的思想,将软件按照模型、视图、控制器来划分 M:Model,模型层,指工程中的JavaBean,作用是处理数据 JavaBean分为两类: 一类称为实体类Bean:专…...
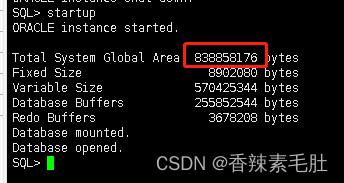
ORACLE内存结构
内存体系结构 目录 内存体系结构 2.1自动内存管理 2.2自动SGA内存管理 2.3手动SGA内存管理 2.3.1数据库缓冲区 2.3.1.1保留池 2.3.1.2回收池 2.3.2共享池 2.3.2.1SQL查询结果和函数查询结果 2.3.2.2库缓存 2.3.2.3数据字典缓存 2.3.3大池 2.3.4 …...

excel常用的几个函数
1、MID函数 通常用来返回返回指定字符串中的子串。 函数公式: MID(string, starting_at, extract_length) String(必填):包含要提取字符的文本字符串 starting_at(必填):文本中要提取的第一个字…...

【Bug】【内存相关】偶然发现一个内存溢出Bug复盘
一、问题 跑自动化用例的时候,uat-sg环境,发现SGW经常会返回 502 Bad Gateway响应 二、原因 经过SRE和BE Dev共同排查,502 是从ALB-- > 后端服务 后端服务无法响应导致,ALB会直接给客户端返回502。 服务端:由于c…...

python读写.pptx文件
1、读取PPT import pptx pptpptx.Presentation(rC:\Users\user\Documents\\2.pptx) # ppt.save(rC:\Users\user\Documents\\1.pptx) # slideppt.slides.add_slide(ppt.slide_layouts[1])# 读取所有幻灯片上的文字 for slide in ppt.slides:for shape in slide.shapes:if shape…...
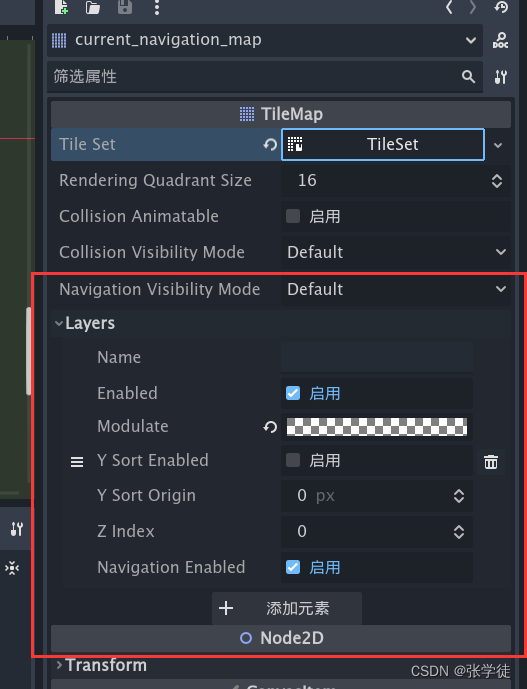
【Godot】【BUG】4.x NavigationAgent 导航不生效
4.2.beta2 试了半天才发现原来默认只对第一个有导航的 TileMap 的第 1 层 生效,而我设置的导航层不是第一层,然后我新建了一个 TileMap 将导航的瓦片设置到这个 TileMap 上了,如图 这样就解决了问题,不用再修改默认设置的东西了&a…...

Rust逆向学习 (1)
文章目录 Hello, Rust Reverse0x01. main函数定位0x02. main函数分析line 1line 2line 3line 4~9 0x03. IDA反汇编0x04. 总结 近年来,Rust语言的热度越来越高,很多人都对Rust优雅的代码和优秀的安全性赞不绝口。对于开发是如此,对于CTF也是如…...

【Golang | reflect】利用反射实现方法的调用
引言 go语言中,如果某个数据类型实现了一系列的方法,如何批量去执行呢,这时候就可以利用反射里的func (v Value) Call(in []Value) []Value 方法。 // Call calls the function v with the input arguments in. // For example, if len(in)…...

Teleport
从官网中获取到的代码如下 App.vue <template><div class"outer"><h3>Tooltips with Vue 3 Teleport</h3><div><MyModal /></div></div> </template> <script setup> import MyModal from "./My…...

flutter与原生 相互通信实战
一、原生和flutter 通信 ios 通信类 CommonUtil.swift import Foundation import Flutterpublic class CommonUtil {public static func emitEvent(channel: FlutterMethodChannel, method: String, type: String, errCode: Int32?, errMsg: String?, data: Any?){safeMa…...

结构光相机原理
结构光相机原理...

ubuntu安装Anaconda
下载 Anaconda 进入 Ubuntu,自己新建下载路径,输入以下命令开始下载 注意,如果不是 x86_64,需要去镜像看对应的版本(https://mirrors.bfsu.edu.cn/anaconda/archive/?CM&OA) wget https://mirrors.…...

【RNA structures】RNA转录的重构和前沿测序技术
文章目录 RNA转录重建1 先简单介绍一下测序相关技术2 Map to Genome Methods2.1 Step1 Mapping reads to the genome2.2 Step2 Deal with spliced reads2.3 Step 3 Resolve individual transcripts and their expression levels 3 Align-de-novo approaches3.1 Step 1: Generat…...

4、Kafka 消费者
5.1 Kafka 消费方式 5.2 Kafka 消费者工作流程 5.2.1 消费者总体工作流程 5.2.2 消费者组原理 Consumer Group(CG):消费者组,由多个consumer组成。形成一个消费者组的条件,是所有消费者的groupid相同。 • 消费者组内…...
CSS3 渐变
CSS3 渐变可以让你在两个或多个指定的颜色之间显示平稳的过渡。 CSS3渐变有两种类型:线性渐变(Linear Gradients)和径向渐变(Radial Gradients)。 线性渐变(Linear Gradients): 线性…...

【Python 千题 —— 基础篇】分割有效信息
题目描述 题目描述 有时候我们需要截取字符串以获取有用的信息,比如对于字符串 “日期:2010-10-29”,我们需要截取后面的 10 个字符来获取日期,以便进行进一步分析。编写一个程序,输入一个字符串,然后输出…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
