【C++】哈希的应用 -- 位图
文章目录
- 一、位图的概念
- 二、位图的实现
- 三、库中的 bitset
- 四、位图的应用
- 五、哈希切割
一、位图的概念
我们以一道面试题来引入位图的概念:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中
我们的第一反应可能是将数据进行排序之后进行二分查找,或者将数据放入unordered_map/unordered_set中,然后再进行查找。但是这两种方式看似能够实现,但是实际上是不行的,因为数据量太大了,在内存中存放不下
40亿个整数,每个整数占4个字节,一共160个字节,而1G大约10亿字节,那么我们存储40个整数就大约需要16G,而我们的内存一般只有4个G,如果我们使用排序之后进行二分查找,那么就需要开辟一个16G大小的数组,显然是无法实现的,如果我们使用红黑树或者哈希表的方式,这也是不行的,因为红黑树每个节点需要存放节点的值,三个指针和颜色,每个节点就需要消耗16个字节,而哈希表中每个桶要存放一个指向下一个节点,也有一定的消耗
我们换一个思考的方式,题目中只要判断一个数在不在,并没有其他的要求,所以我们不需要将这些树存储下来,只需要用一个值来对他们进行标记即可,而标记一个数只需要一个比特位即可,如果二进制比特位为1,则表示存在,为0表示不存在
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
二、位图的实现
对于位图,一般我们只需要提供一下三个接口即可:
1.set : 用于将某一数值对应的比特位置为1,即进行标记(插入数据)
2.reset:将某一数值对应的比特位置为0,即删除标记(删除数据)
3.test : 用于测试某一数值对应的比特位是否为1,即查找数据
这里我们需要一个非类型模板参数–N是给定的数据的范围,不是数据的个数,因为C++中最小的数据类型是char,占一个字节的空间,一个字节占8个比特位,可以用于标记8个位置。我们可以用一个vector来进行存储数据,所以我们在构造函数中我们将vector resize到N/8+1即可,加1是因为C++中的除法是整除法,即直接舍弃余数,而我们这里应该采取进1法,即需要多开辟一个空间。此外,我们还可以将vector中的数据的类型定义为int,此时我们开辟空间的时候应该resize到N/32+1
对于三个重要接口的实现,我们使用目标值x/8就可以得到x应该被映射到哪一个下标,即在第几个char的位置,x%8就可以得到x应该被映射到该下标的第几个比特位,然后再将对应的位置置为1或0即可
对于set:我们可以使用或等的方法,找到一个数,这个数的第j个比特位(j为在下标中的第几个位置)为1,其他的位置为0,我们使用1向左移动j为即可,然后再进行或等
对于reset:我们可以使用与等的方法,找到一个数,第j为0,其他位为1,我们只需要将1向左移动j位i,然后再进行按位取反即可,然后再进行与等
对于test:我们知道,在逻辑关系中,0为假,非0为真,那么我们就可以将那个位置的数进行与,注意是与,不是与等,与1左移j为,如果那个位置为1,那么都为0,判断为假,如果那个位置不为0,与之后也不为0,此时转换为bool类型,为真,这里会进行整形提升,但是将一个数从0提升到非0或者从非0提升到0,所以符号我们的要求
代码实现如下:
namespace hdp
{template<size_t N>class bitset{public:bitset(){_bits.resize(N / 8 + 1, 0);}void set(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] |= (1 << j);}void reset(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 8;size_t j = x % 8;return _bits[i] & (1 << j);}private:vector<char> _bits;};
}
有了位图之后,我们就可以解决上面的面试题了–由于题目中说明了数据是无符号整数,那么我们就可以将N定义为-1(有符号的-1等于无符号的最大值),然后我们只需要将这40亿个数据依次进行set,然后进行test即可
无符号的最大值大约为42亿九千万,也就是需要这么多的比特位来进行标记,计算得大约需要5亿字节,即512M,这是可以在内存中存放得下的
三、库中的 bitset
C++提供了类似于位图的东西–位的集合–bitset,它的功能比我们实现的更加的丰富,但是主要功能还是set,reset和test


四、位图的应用
位图主要运用于一下几个方面:
1.快速查找某个数据是否在一个集合中
2.排序 + 去重
3.求两个集合的交集、并集等
4.操作系统中磁盘块标记
我们来看看下面几道位图应用的题目:
1.给定100亿个整数,设计算法找到只出现一次的整数?
我们发现,使用传统的位图并不能解决这个问题,因为位图只能表示存在和不存在,只能够表示两种状态,这个问题中,就存在多种状态,但是我们可以将上面的问题分为3种状态–没有出现,出现1次,出现一次以上。那么我们就可以使用两个位图结合在一起,使用两个比特位来进行标识,两个比特位最多可以标识4种状态,我们取3种即可:
00:没有出现
01:出现1次
10:出现1次以上
代码实现如下:
template<size_t N>
class twobitset
{
public:void set(size_t x){if (!_bs1.test(x) && !_bs2.test(x)) //00{_bs2.set(x);//01}else if (!_bs1.test(x) && _bs2.test(x)) //01{_bs1.set(x);_bs2.reset(x); //10}}private:bitset<N> _bs1;bitset<N> _bs2;
};
2.1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
这道题和上面求只出现一次的数字的思路一致,这里我们需要将出现0次,1次,2次,2次以上的状态都表示处出来,使用两个标记位即可
template<size_t N>
class twobitset
{
public:void set(size_t x){if (!_bs1.test(x) && !_bs2.test(x)) //00{_bs2.set(x);//01}else if (!_bs1.test(x) && _bs2.test(x)) //01{_bs1.set(x);_bs2.reset(x); //10}else if(_bs1.test(x) && !_bs2.test(x)) // 10{_bs1.set(x);_bs2.set(x); //11}}private:bitset<N> _bs1;bitset<N> _bs2;
};
3.给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
我们可以将第一个文件的数据全部映射到一个位图中,然后再遍历取出第二个位图中的数据进行test即可,返回true的数据即为交集,但是这样就会得到许多重复的数据,所以最终的结果需要进行去重处理。我们也可以使用两个位图分别进行映射,然后进行遍历,两者进行与运算,为1则为交集的数据
五、哈希切割
对于下面这道题目:
给一个超过100G大小的log fifile, log中存着IP地址, 设计算法找到出现次数最多的IP地址?
和前面我们的题目不同,这道题我们不能使用位图来解决,因为我们不知道相同的ip会出现多少次,所以就无法确定使用多少个比特位来进行标记
100G数据太大内存放不下,我们能不能将这个文件平均分为100分大小的文件,这样每个问题都只有一个G的大小,此时再依次插入map中进行统计次数,这样其实也是不行的,因为在统计下一个小的文件时,我们需要将之前的文件的统计结果即map中的数据进行clear,否则就会因为数据过多导致内存不足的情况,这样就不能够很好的统计出IP出现的次数。
我们可以想办法将相同的IP放入同一个小文件中,即我们可以使用哈希切割的方法–先使用字符哈希函数将IP转换为整数,然后再使用除留余数法将100G文件的IP地址划分到不同的小文件中
size_t Ai = HashFunc(IP) % 100;
经过哈希切割之后,相同的IP一定会被划分到同一个小文件中,因为相同的字符串经过哈希映射之后一定会得到相同的整数,那么模出来的结果也也一定相同,即会在同一个小文件中,但是不同的IP也可能会被划分到同一个文件中,因为会发生哈希冲突,此时文件的大小就可能会操作一个G,并且划分非结果有两种:
1.子文件中有许多相同的IP地址,此时我们可以直接使用map统计这些IP地址的数量(所有相同的IP地址一定会出现在同一个子文件中)
2.子文件中有许不同的IP地址,大多是不重复的,map统计不下,那么此时我们就需要换一个哈希函数,递归再切分
使用map统计,如果是第一种情况,可以统计出来的,不会报错
如果是第二种情况,map的insert插入失败,那是没有内存,相当于new节点失败,new失败会抛异常
最终出现次数最多的那个IP地址会被全部映射到某一个子文件中,我们对子文件使用map进行统计就可以得到其出现的次数
相关文章:

【C++】哈希的应用 -- 位图
文章目录 一、位图的概念二、位图的实现三、库中的 bitset四、位图的应用五、哈希切割 一、位图的概念 我们以一道面试题来引入位图的概念: 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中 我…...
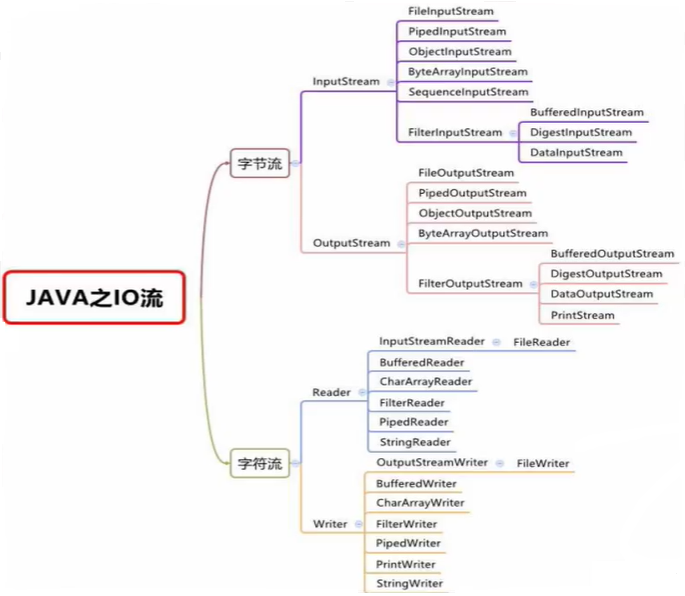
系列二、IO流原理及流的分类
一、概述 IO是Input、Output的缩写,IO流技术是非常实用的技术,用于处理数据传输,例如读写文件,网络通讯等。在Java程序中,对于数据的输入/输出操作以"流(stream)"的方式进行ÿ…...

【算法教程】排列与组合的实现
数据准备 在讲排列与组合之前,我们先定义数据元素类型Fruit class Fruit{constructor(name,price){this.name namethis.price price} }排列 对N个不同元素进行排序,总共有多少不同的排列方式? Step1: 从N个元素中取1个,共N种…...

uniapp实现简单的九宫格抽奖(附源码)
效果展示 uniapp实现大转盘抽奖 实现步骤: 1.该页面可设置8个奖品,每个奖品可设置中奖机会的权重,如下chance越大,中奖概率越高(大于0) // 示例代码 prizeList: [{id: 1,image: "https://img.alicdn…...
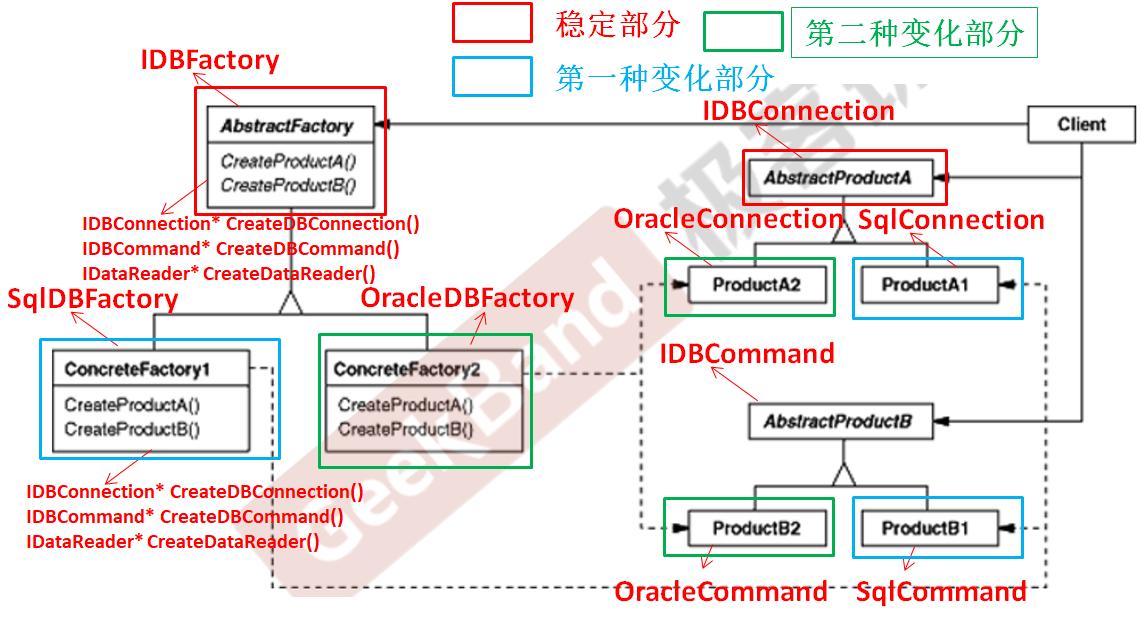
C++设计模式_09_Abstract Factory 抽象工厂
与上篇介绍的Factory Method工厂方法模式一样,Abstract Factory 抽象工厂模式也属于典型的“对象创建模式”模式,解决的问题也极其相似,在理解了Factory Method工厂方法模式的基础上再去理解Abstract Factory 抽象工厂模式就会变得更加容易。…...
一些前端面试思考
回流和重绘 先牢记这句话,回流必将引起重绘,而重绘不一定会引起回流。回流的代价要远大于重绘。 当你给一个元素更换颜色,这样的行为是不会影响页面布局的,DOM树不会变化,但颜色变了,渲染树得重新渲染页面&…...
)
Spring MVC(上)
1、Spring MVC简介: MVC是一种软件架构的思想,将软件按照模型、视图、控制器来划分 M:Model,模型层,指工程中的JavaBean,作用是处理数据 JavaBean分为两类: 一类称为实体类Bean:专…...
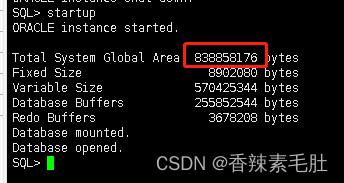
ORACLE内存结构
内存体系结构 目录 内存体系结构 2.1自动内存管理 2.2自动SGA内存管理 2.3手动SGA内存管理 2.3.1数据库缓冲区 2.3.1.1保留池 2.3.1.2回收池 2.3.2共享池 2.3.2.1SQL查询结果和函数查询结果 2.3.2.2库缓存 2.3.2.3数据字典缓存 2.3.3大池 2.3.4 …...

excel常用的几个函数
1、MID函数 通常用来返回返回指定字符串中的子串。 函数公式: MID(string, starting_at, extract_length) String(必填):包含要提取字符的文本字符串 starting_at(必填):文本中要提取的第一个字…...

【Bug】【内存相关】偶然发现一个内存溢出Bug复盘
一、问题 跑自动化用例的时候,uat-sg环境,发现SGW经常会返回 502 Bad Gateway响应 二、原因 经过SRE和BE Dev共同排查,502 是从ALB-- > 后端服务 后端服务无法响应导致,ALB会直接给客户端返回502。 服务端:由于c…...

python读写.pptx文件
1、读取PPT import pptx pptpptx.Presentation(rC:\Users\user\Documents\\2.pptx) # ppt.save(rC:\Users\user\Documents\\1.pptx) # slideppt.slides.add_slide(ppt.slide_layouts[1])# 读取所有幻灯片上的文字 for slide in ppt.slides:for shape in slide.shapes:if shape…...
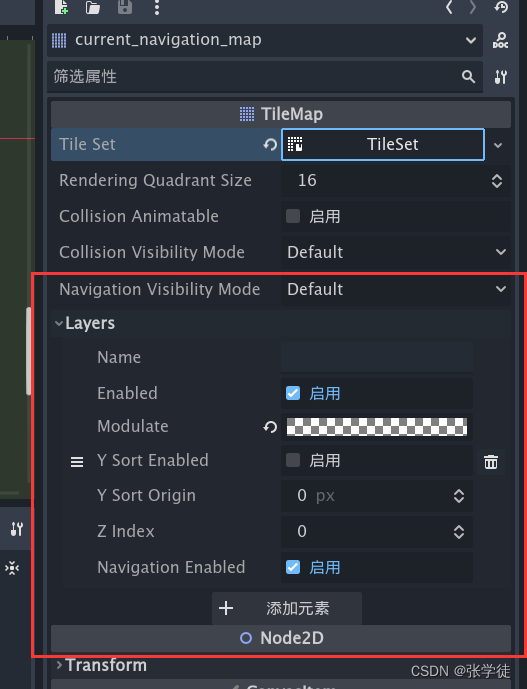
【Godot】【BUG】4.x NavigationAgent 导航不生效
4.2.beta2 试了半天才发现原来默认只对第一个有导航的 TileMap 的第 1 层 生效,而我设置的导航层不是第一层,然后我新建了一个 TileMap 将导航的瓦片设置到这个 TileMap 上了,如图 这样就解决了问题,不用再修改默认设置的东西了&a…...

Rust逆向学习 (1)
文章目录 Hello, Rust Reverse0x01. main函数定位0x02. main函数分析line 1line 2line 3line 4~9 0x03. IDA反汇编0x04. 总结 近年来,Rust语言的热度越来越高,很多人都对Rust优雅的代码和优秀的安全性赞不绝口。对于开发是如此,对于CTF也是如…...

【Golang | reflect】利用反射实现方法的调用
引言 go语言中,如果某个数据类型实现了一系列的方法,如何批量去执行呢,这时候就可以利用反射里的func (v Value) Call(in []Value) []Value 方法。 // Call calls the function v with the input arguments in. // For example, if len(in)…...

Teleport
从官网中获取到的代码如下 App.vue <template><div class"outer"><h3>Tooltips with Vue 3 Teleport</h3><div><MyModal /></div></div> </template> <script setup> import MyModal from "./My…...

flutter与原生 相互通信实战
一、原生和flutter 通信 ios 通信类 CommonUtil.swift import Foundation import Flutterpublic class CommonUtil {public static func emitEvent(channel: FlutterMethodChannel, method: String, type: String, errCode: Int32?, errMsg: String?, data: Any?){safeMa…...

结构光相机原理
结构光相机原理...

ubuntu安装Anaconda
下载 Anaconda 进入 Ubuntu,自己新建下载路径,输入以下命令开始下载 注意,如果不是 x86_64,需要去镜像看对应的版本(https://mirrors.bfsu.edu.cn/anaconda/archive/?CM&OA) wget https://mirrors.…...

【RNA structures】RNA转录的重构和前沿测序技术
文章目录 RNA转录重建1 先简单介绍一下测序相关技术2 Map to Genome Methods2.1 Step1 Mapping reads to the genome2.2 Step2 Deal with spliced reads2.3 Step 3 Resolve individual transcripts and their expression levels 3 Align-de-novo approaches3.1 Step 1: Generat…...

4、Kafka 消费者
5.1 Kafka 消费方式 5.2 Kafka 消费者工作流程 5.2.1 消费者总体工作流程 5.2.2 消费者组原理 Consumer Group(CG):消费者组,由多个consumer组成。形成一个消费者组的条件,是所有消费者的groupid相同。 • 消费者组内…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
