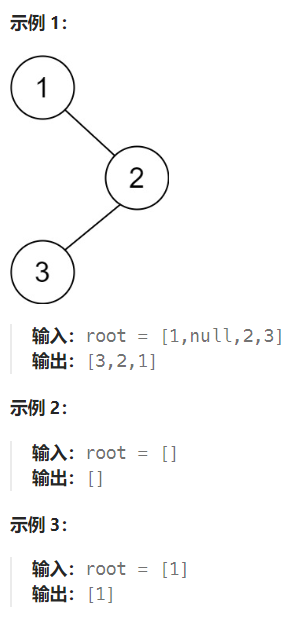
【LeetCode】145. 二叉树的后序遍历 [ 左子树 右子树 根结点]
题目链接
文章目录
- Python3
- C++


Python3
方法一: 递归 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:"""后序遍历 [ 左子树 右子树 根结点 ] 递归 """def postorder(node):if not node:return postorder(node.left) # 左子树 postorder(node.right) # 右子树ans.append(node.val) # 根结点ans = []postorder(root)return ans
方法二: 迭代 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:"""后序遍历 [左子树 右子树 根] 迭代"""ans = []stack = []cur = rootpre = Nonewhile cur or stack:while cur:stack.append(cur)cur = cur.left # 左cur = stack.pop()if not cur.right or cur.right == pre: ## 右边 已遍历完ans.append(cur.val) # 根 pre = cur cur = None else:stack.append(cur)cur = cur.right # 右return ans

方法三: Morris ⟮ O ( n ) 、 O ( 1 ) ⟯ \lgroup O(n)、O(1) \rgroup ⟮O(n)、O(1)⟯

写法一
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:""" 后序遍历 [ 左子树 右子树 根 ] Morris O(N) O(1)"""### 写法一 根 右 左 反转结果列表 # 根据 前序遍历 修改ans = []cur, pre = root, None while cur:if not cur.right:ans.append(cur.val) ##cur = cur.left# 有右孩子else:# 找 pre pre = cur.right while pre.left and pre.left != cur:pre = pre.left if not pre.left: ## 找到 mostleftpre.left = curans.append(cur.val) ## cur = cur.rightelse:pre.left = None cur = cur.leftreturn ans[::-1]
写法二
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:""" 后序遍历 [ 左子树 右子树 根 ] Morris O(N) O(1)"""## 需要 增加 一个 反转模块def addPath(node: TreeNode):count = 0while node:count += 1ans.append(node.val)node = node.righti, j = len(ans) - count, len(ans) - 1while i < j:ans[i], ans[j] = ans[j], ans[i]i += 1j -= 1### ans = []cur, pre = root, None while cur:if not cur.left:cur = cur.right # 有左孩子else:# 找 pre pre = cur.left while pre.right and pre.right != cur:pre = pre.right if not pre.right:pre.right = curcur = cur.left else:pre.right = None addPath(cur.left) ## cur = cur.right addPath(root) ## return ans C++
方法一: 递归 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 子模块void postorder(TreeNode* node, vector<int> &ans){if (node == nullptr){return;}postorder(node->left, ans);postorder(node->right, ans);ans.emplace_back(node->val);}// 主模块vector<int> postorderTraversal(TreeNode* root) {vector<int> ans;postorder(root, ans);return ans;}
};
方法二: 迭代 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> ans;stack<TreeNode*>stk;TreeNode* cur = root;TreeNode* pre = nullptr;while (cur != nullptr || !stk.empty()){while (cur != nullptr){stk.emplace(cur);cur = cur->left;}cur = stk.top();stk.pop();if (cur->right == nullptr || cur->right == pre){// 右子树 遍历完,处理根结点ans.emplace_back(cur->val);pre = cur;cur = nullptr;}else{// 右子树stk.emplace(cur);cur = cur->right;}}return ans;}
};
方法三: Morris ⟮ O ( n ) 、 O ( 1 ) ⟯ \lgroup O(n)、O(1) \rgroup ⟮O(n)、O(1)⟯
写法一
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> ans;TreeNode* cur = root;TreeNode* pre = nullptr;while (cur != nullptr){if (cur->right == nullptr){ans.emplace_back(cur->val);cur = cur->left;}else{// 找 pre pre = cur->right;while (pre->left != nullptr && pre->left != cur){pre = pre->left;}if (pre->left == nullptr){pre->left = cur;ans.emplace_back(cur->val);cur = cur->right;}else{pre->left = nullptr;cur = cur->left;}}}reverse(ans.begin(), ans.end()); // 该函数为 void ,不能直接返回return ans;}
};
写法二
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 子模块void addPath(TreeNode* node, vector<int> &ans){int count = 0;while (node != nullptr){count += 1;ans.emplace_back(node->val);node = node->right;}int i = ans.size() - count, j = ans.size() - 1;while (i < j){swap(ans[i], ans[j]);i += 1;j -= 1;}}// 主模块vector<int> postorderTraversal(TreeNode* root) {vector<int> ans;TreeNode* cur = root;TreeNode* pre = nullptr;while (cur != nullptr){if (cur->left == nullptr){cur = cur->right;}else{//找 pre pre = cur->left;while (pre->right != nullptr && pre->right != cur){pre = pre->right;}if (pre->right == nullptr){pre->right = cur;cur = cur->left;}else{pre->right = nullptr;addPath(cur->left, ans);cur = cur->right;}}}addPath(root, ans);return ans;}
};
相关文章:

【LeetCode】145. 二叉树的后序遍历 [ 左子树 右子树 根结点]
题目链接 文章目录 Python3方法一: 递归 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯方法二: 迭代 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯方法三: Morris ⟮ O ( n ) 、 O ( 1 ) ⟯ \lgroup O(n)、O(1) \rgroup ⟮O(n)、O(1)⟯写…...

Unity之ShaderGraph如何实现触电电流效果
前言 之前使用ASE做过一个电流效果的shader,今天我们通过ShaderGraph来实现一个电流效果。 效果如下: 关键节点 Simple Noise:根据输入UV生成简单噪声或Value噪声。生成的噪声的大小由输入Scale控制。 Power:返回输入A的结果…...
【微信小程序调试工具试用】
【微信小程序调试工具试用】 试用大佬开发的dll拿到某物小程序sign签名 (过于简单 大佬勿喷)本次工具分享到此结束 什么是爬虫逆向? 试用大佬开发的dll拿到某物小程序sign签名 (过于简单 大佬勿喷) 1 如图 下面小程序…...
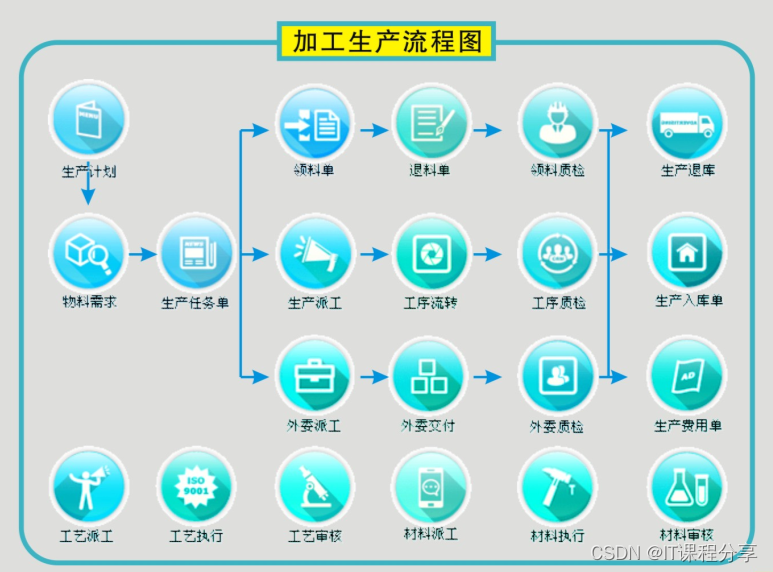
机械生产ERP管理系统
机械生产ERP管理系统 功能介绍: 生产管理: 1.灵活自定义生产车间、成本费用类型、成本项目; 2.方便直观的物料清单(BOM),并可以逆向展开; 3.科学实用的物料需求计划(MRP)&#x…...
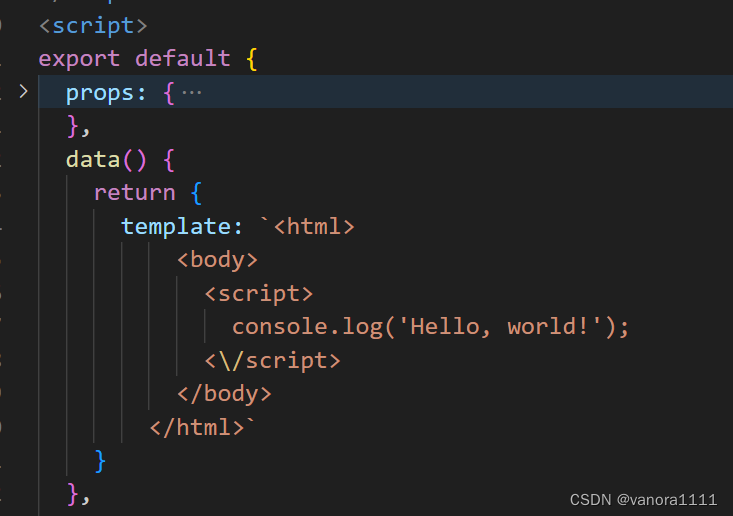
Vue 模板字符串碰到script无法识别,报错Parsing error: Unterminated template.
需求: 将js代码完整的显示在界面上,包括标签 代码如下: 报错信息如下: 我们在上图中可以看到模板字符串加入了script标签后会报错 原因:运行JS的时候由上至下,先识别模板字符串里面的script标签…...

AWS SAP-C02教程5--基础中间件
在AWS中除了计算、存储、网络之外,还有一些组件非常重要,包括基础组件、消息队列组件、日志组件、编排组件等,接下来就通过分成几个不同类别(这个分类按照AWS的大概分类进行分类,并无统一标准,只是具备一定相同功能归类在一起方便记忆) 目录 1 消息中间件1.1 SQS1.1.1 …...

2022年亚太杯APMCM数学建模大赛E题有多少核弹可以摧毁地球求解全过程文档及程序
2022年亚太杯APMCM数学建模大赛 E题 有多少核弹可以摧毁地球 原题再现 1945年8月6日,第二次世界大战即将结束。为了尽快结束战争,美国在日本广岛投下了下一颗名为“小男孩”的原子弹。这样一颗原子弹在广岛炸死了20万人,广岛的所有建筑物都…...

论文阅读[51]通过深度学习快速识别荧光组分
【论文基本信息】 标题:Fast identification of fluorescent components in three-dimensional excitation-emission matrix fluorescence spectra via deep learning 标题译名:通过深度学习快速识别 三维激发-发射矩阵荧光光谱中的荧光组分 期刊与年份&…...

解决Flutter启动一直卡在 Running Gradle task ‘assembleDebug‘...
前言 新建了一个Flutter工程后,Run APP 却一直卡在了Running Gradle task ‘assembleDebug’… 这里。百度查询原因是因为 Gradle 的 Maven 仓库在国外, 因此需要使用阿里云的镜像地址。 1、修改项目中android/build.gradle文件 将 buildscript.repositories 下面…...

c/c++的include机制简述
一 引言 做c/c编程的对#include指令都不会陌生,绝大多数也都知道如何使用,但我相信仍有人对此是一知半解, C: #include <stdio.h>C: #include <iostream> 表示包含C/C标准输入头文件。包含指令不仅仅限于.h头文件,可…...

YOLOv5算法改进(16)— 增加小目标检测层 | 四头检测机制(包括代码+添加步骤+网络结构图)
前言:Hello大家好,我是小哥谈。小目标检测层是指在目标检测任务中用于检测小尺寸目标的特定网络层。由于小目标具有较小的尺寸和低分辨率,它们往往更加难以检测和定位。YOLOv5算法的检测速度与精度较为平衡,但是对于小目标的检测效果不佳,根据一些论文,我们可以通过增加检…...

【计网 EMail】计算机网络 EMail协议详解:中科大郑烇老师笔记 (五)
目录 0 引言1 电子邮件EMail1.1 组成1.2 SMTP协议1.3 案例:Alice给Bob发送报文1.4 SMTP总结1.5 邮件报文格式1.6 POP3协议和IMAP协议 🙋♂️ 作者:海码007📜 专栏:计算机四大基础专栏📜 其他章节…...

算法随想录算法训练营第四十三天|300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组
300.最长递增子序列 题目:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,…...

Nginx配置限流
Nginx配置限流 Nginx有限流功能,是基于漏桶算法实现的 limit_req_zone是配置在http模块中的 #设置限流 zone用来定义ip状态和url访问频率的共享区域,其中mylimit为区域名称,冒号后为区域大小,16000个IP地址的状态信息大约是1M&am…...
】25 - QNX Ethernet MAC 驱动 之 emac_isr_thread_handler 中断处理函数源码分析)
【SA8295P 源码分析 (四)】25 - QNX Ethernet MAC 驱动 之 emac_isr_thread_handler 中断处理函数源码分析
【SA8295P 源码分析】25 - QNX Ethernet MAC 驱动 之 emac_isr_thread_handler 中断处理函数源码分析 一、emac 中断上半部:emac_isr()二、emac 中断下半部:emac_isr_thread_handler()2.1 emac 中断下半部:emac_isr_sw()系列文章汇总见:《【SA8295P 源码分析 (四)】网络模块…...
C#,数值计算——分类与推理Phylo_clc的计算方法与源程序
1 文本格式 using System; using System.Collections.Generic; namespace Legalsoft.Truffer { public class Phylo_clc : Phylagglom { public override void premin(double[,] d, int[] nextp) { } public override double dminfn(double[…...

力扣第455题 分发饼干 c++ 贪心 经典题
题目 455. 分发饼干 简单 相关标签 贪心 数组 双指针 排序 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干…...
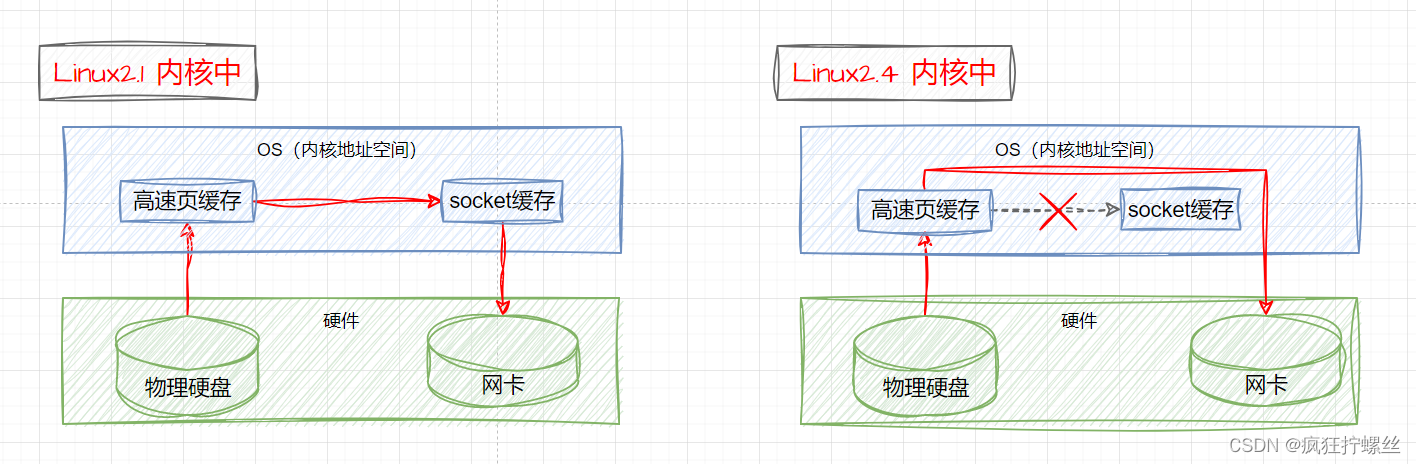
Netty系列教程之NIO基础知识
近30集的孙哥视频课程,看完一集整理一集来的,内容有点多,请大家放心食用~ 1. 网络通讯的演变 1.1 多线程版网络通讯 在传统的开发模式中,客户端发起一个 HTTP 请求的过程就是建立一个 socket 通信的过程,服务端在建立…...

【题解 树形dp 拆位】 树上异或
「KDOI-06-S」树上异或 题目描述 给定一棵包含 n n n 个节点的树,第 i i i 个点有一个点权 x i x_i xi。 对于树上的 n − 1 n-1 n−1 条边,每条边选择删除或不删除,有 2 n − 1 2^{n-1} 2n−1 种选择是否删除每条边的方案。 对于…...
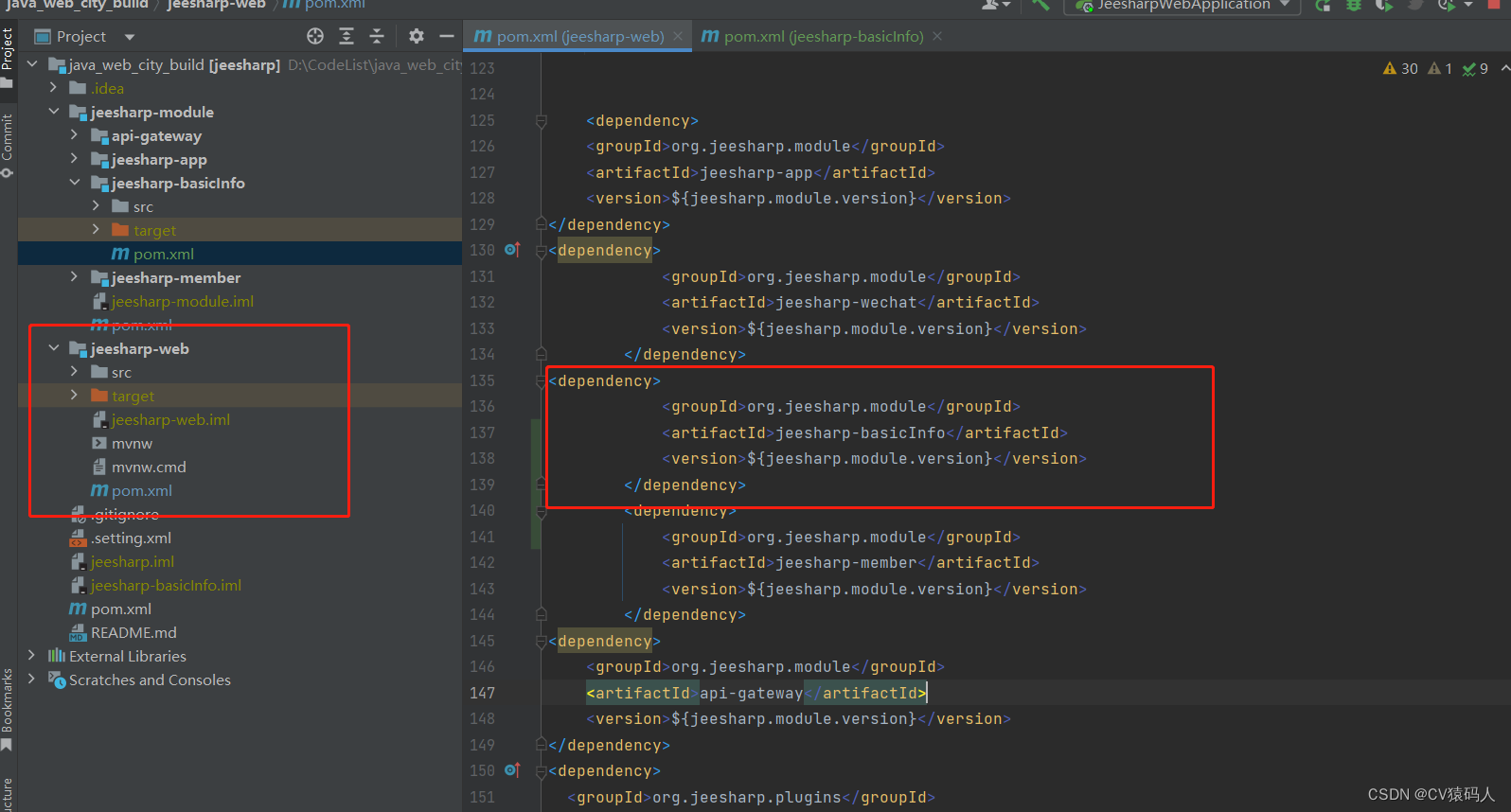
SpringBoot项目访问后端页面404
检查项目的路径和mapper映射路径没问题后,发现本级pom文件没有加入web启动模块的pom文件中 maven做项目控制时,要注意将maven模块加入到web启动模块中...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
