【题解 树形dp 拆位】 树上异或
「KDOI-06-S」树上异或
题目描述
给定一棵包含 n n n 个节点的树,第 i i i 个点有一个点权 x i x_i xi。
对于树上的 n − 1 n-1 n−1 条边,每条边选择删除或不删除,有 2 n − 1 2^{n-1} 2n−1 种选择是否删除每条边的方案。
对于每种删除边的方案,设删除后的图包含 k k k 个连通块,定义这个方案的权值为图中连通块点权异或和的乘积。形式化地说,若这张图包含连通块 C 1 , C 2 , … , C k C_1,C_2,\ldots,C_k C1,C2,…,Ck,其中 C i C_i Ci 是第 i i i 个连通块的顶点集合,设 v i = ⨁ u ∈ C i x u v_i=\bigoplus_{u\in C_i} x_u vi=⨁u∈Cixu,则这个方案的权值为 v 1 × v 2 × ⋯ × v k v_1\times v_2\times \cdots\times v_k v1×v2×⋯×vk。
求这 2 n − 1 2^{n-1} 2n−1 种删除边的方案的权值之和,答案对 998 244 353 998~244~353 998 244 353 取模。
输入格式
从标准输入读入数据。
输入的第一行包含一个正整数 n n n,表示树的节点个数。
第二行 n n n 个非负整数 x 1 , x 2 , … , x n x_1,x_2,\ldots,x_n x1,x2,…,xn,表示每个点的点权。
第三行 n − 1 n-1 n−1 个正整数 f 2 , f 3 , … , f n f_2,f_3,\ldots,f_n f2,f3,…,fn,表示节点 i i i 与 f i f_{i} fi 之间有一条无向边。
输出格式
输出到标准输出。
输出包含一行一个整数,表示所有 2 n − 1 2^{n-1} 2n−1 种删除边的方案的权值之和,答案对 998 244 353 998~244~353 998 244 353 取模。
样例 #1
样例输入 #1
3
1 2 3
1 1
样例输出 #1
19
样例 #2
样例输入 #2
5
3 4 5 6 7
1 1 2 2
样例输出 #2
5985
提示
【样例解释 #1】
有四种删除边的方案:
- 不删除边:图有且仅有一个连通块,权值为 1 ⊕ 2 ⊕ 3 = 0 1\oplus2\oplus3=0 1⊕2⊕3=0。
- 删除 ( 1 , 2 ) (1,2) (1,2) 一条边:图包含两个连通块,权值为 ( 1 ⊕ 3 ) × 2 = 4 (1\oplus3)\times2=4 (1⊕3)×2=4。
- 删除 ( 1 , 3 ) (1,3) (1,3) 一条边:图包含两个连通块,权值为 ( 1 ⊕ 2 ) × 3 = 9 (1\oplus2)\times3=9 (1⊕2)×3=9。
- 删除 ( 1 , 2 ) (1,2) (1,2), ( 1 , 3 ) (1,3) (1,3) 两条边:图包含三个连通块,权值为 1 × 2 × 3 = 6 1\times2\times3=6 1×2×3=6。
所有方案权值的总和为 0 + 4 + 9 + 6 = 19 0+4+9+6=19 0+4+9+6=19。
【样例 #3】
见选手目录下的 xor/xor3.in 与 xor/xor3.ans。
这个样例满足测试点 6 ∼ 7 6\sim7 6∼7 的条件限制。
【样例 #4】
见选手目录下的 xor/xor4.in 与 xor/xor4.ans。
这个样例满足测试点 8 8 8 的条件限制。
【样例 #5】
见选手目录下的 xor/xor5.in 与 xor/xor5.ans。
这个样例满足测试点 9 9 9 的条件限制。
【样例 #6】
见选手目录下的 xor/xor6.in 与 xor/xor6.ans。
这个样例满足测试点 19 ∼ 21 19\sim21 19∼21 的条件限制。
【数据范围】
对于所有数据保证: 1 ≤ n ≤ 5 × 1 0 5 1\leq n\leq5\times10^5 1≤n≤5×105, 0 ≤ x i ≤ 1 0 18 0\leq x_i\leq10^{18} 0≤xi≤1018, 1 ≤ f i < i 1\leq f_i<i 1≤fi<i。
| 测试点编号 | n ≤ n\leq n≤ | x i x_i xi | 特殊性质 |
|---|---|---|---|
| 1 ∼ 2 1\sim2 1∼2 | 12 12 12 | ≤ 1 0 9 \leq10^9 ≤109 | 无 |
| 3 3 3 | 2000 2000 2000 | = 1 =1 =1 | 无 |
| 4 4 4 | 1 0 5 10^5 105 | = 1 =1 =1 | A |
| 5 5 5 | 1 0 5 10^5 105 | = 1 =1 =1 | B |
| 6 ∼ 7 6\sim7 6∼7 | 1 0 5 10^5 105 | = 1 =1 =1 | 无 |
| 8 8 8 | 1 0 5 10^5 105 | ≤ 7 \leq7 ≤7 | A |
| 9 9 9 | 1 0 5 10^5 105 | ≤ 7 \leq7 ≤7 | B |
| 10 ∼ 11 10\sim11 10∼11 | 1 0 5 10^5 105 | ≤ 7 \leq7 ≤7 | 无 |
| 12 ∼ 16 12\sim16 12∼16 | 200 200 200 | ≤ 8191 \leq8191 ≤8191 | 无 |
| 17 17 17 | 1 0 5 10^5 105 | ≤ 1 0 9 \leq10^9 ≤109 | A |
| 18 18 18 | 1 0 5 10^5 105 | ≤ 1 0 9 \leq10^9 ≤109 | B |
| 19 ∼ 21 19\sim21 19∼21 | 1 0 5 10^5 105 | ≤ 1 0 9 \leq10^9 ≤109 | 无 |
| 22 ∼ 25 22\sim25 22∼25 | 5 × 1 0 5 5\times10^5 5×105 | ≤ 1 0 18 \leq10^{18} ≤1018 | 无 |
- 特殊性质 A:保证对于任意 1 < i ≤ n 1< i\le n 1<i≤n, f i = i − 1 f_i=i-1 fi=i−1。
- 特殊性质 B:保证对于任意 1 < i ≤ n 1< i\le n 1<i≤n, f i = 1 f_i=1 fi=1。
【提示】
⊕ \oplus ⊕ 表示按位异或运算。
本题输入输出量较大,请使用适当的 I/O 方式。
请注意常数因子对程序运行效率产生的影响。
分析:
树上问题一下子不好分析,我们首先从链的问题来考虑
一一枚举所有的断边情况,时间复杂度是 O ( 2 n ) O(2^n) O(2n),显然爆炸
我们考虑dp
设 f i f_i fi表示第i个点的答案( ∑ ∏ \sum\prod ∑∏)
我们考虑枚举前面的断边,
f i = ∑ f j ∗ ( s i x o r s j ) f_i=\sum f_j*(s_i xor s_j) fi=∑fj∗(sixorsj)
这样 O ( n 2 ) O(n_2) O(n2)就能把问题全部解决,但是还是不够
怎么办?
我们考虑拆位
设 g i , j , 0 / 1 g_{i,j,0/1} gi,j,0/1表示第i个点,i所在的联通块的点权二进制的第j位为0/1时,与i所在连通块断开的连通块的答案是多少
对于当前边,我们有断和不断两个选择,如果不断,那么i的前一个点也包含在了i所在的连通块上,需要根据情况去转移对应点的01值,如果当前边断掉,那么前一个点的二进制值就当做0来考虑
于是我们进行以下转移:

感谢大佬的博客
而后f加起来即可
#include<bits/stdc++.h>
using namespace std;#define ll long longll Mo = 998244353;const int N = 5e5+10;
int n;
ll a[N],f[N],g[N][64][2];
struct Node{int y,Next;
}e[2*N];
int len , Linkk[N];#define gc getchar()
ll read(){ll s = 0 , ff = 0; char ch = gc;while (ch < '0' || ch > '9') ff|=ch == '-' , ch = gc;while (ch >= '0' && ch <= '9') s = s*10+ch-48 , ch = gc;return ff?-s:s;
} void Insert(int x,int y){e[++len] = (Node){y,Linkk[x]};Linkk[x] = len;
}void Dfs(int x,int faa){for (int i = 0; i < 64; i++){int xx = (a[x]>>i)&1;g[x][i][xx] = 1;}for (int j = Linkk[x]; j; j = e[j].Next){int y = e[j].y;if (y == faa) continue;Dfs(y,x);for (int i = 0; i < 64; i++){int t0 = g[x][i][0] , t1 = g[x][i][1];g[x][i][0] = (t0*((g[y][i][0]+f[y]))+t1*g[y][i][1])%Mo;g[x][i][1] = (t1*((g[y][i][0]+f[y]))+t0*g[y][i][1])%Mo;}}for (int i = 0; i < 64; i++)f[x] = (f[x]+(1ll<<i)%Mo*g[x][i][1])%Mo;return;
}signed main(){n = read();for (int i = 1; i <= n; i++) a[i] = read();for (int i = 2,x; i <= n; i++)x = read(),Insert(i,x),Insert(x,i);Dfs(1,0);printf("%lld",f[1]%Mo);return 0;
}
相关文章:

【题解 树形dp 拆位】 树上异或
「KDOI-06-S」树上异或 题目描述 给定一棵包含 n n n 个节点的树,第 i i i 个点有一个点权 x i x_i xi。 对于树上的 n − 1 n-1 n−1 条边,每条边选择删除或不删除,有 2 n − 1 2^{n-1} 2n−1 种选择是否删除每条边的方案。 对于…...
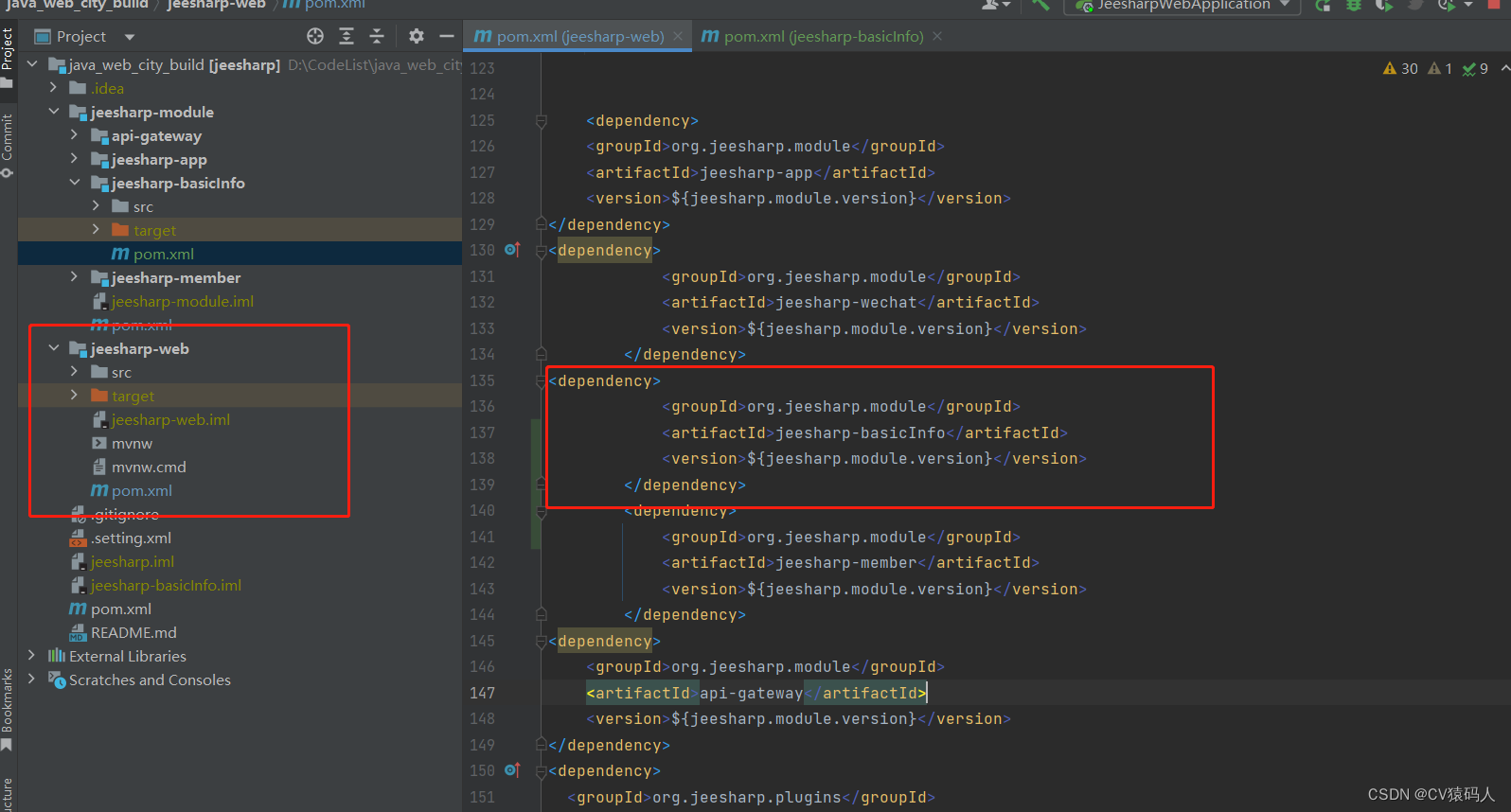
SpringBoot项目访问后端页面404
检查项目的路径和mapper映射路径没问题后,发现本级pom文件没有加入web启动模块的pom文件中 maven做项目控制时,要注意将maven模块加入到web启动模块中...
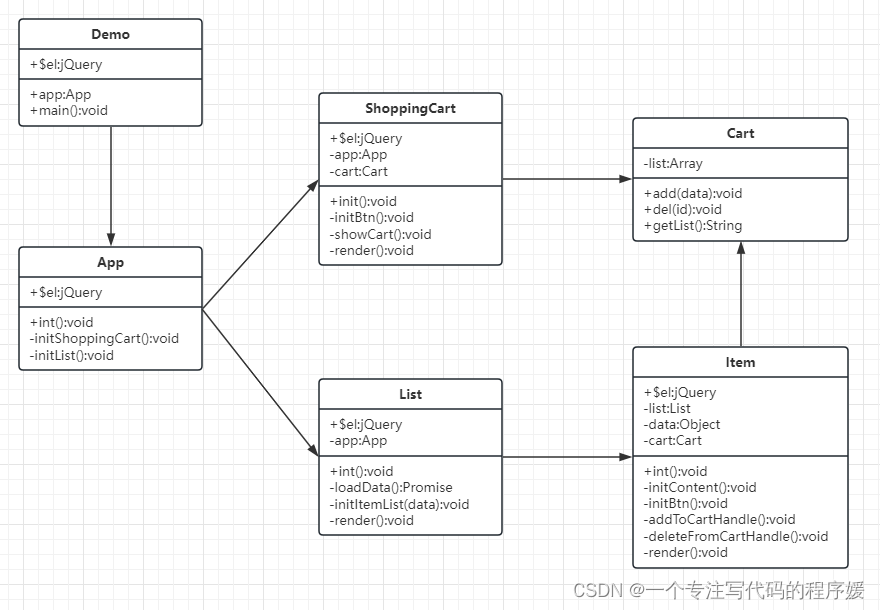
设计模式-综合应用(一)
介绍 使用jQuery做一个模拟购物车的示例 用到的设计模式 工厂模式 单例模式装饰器模式 观察者模式状态模式 模板方法模式 代理模式 UML类图...

大数据Flink(一百):SQL自定义函数(UDF)和标量函数(Scalar Function)
文章目录 SQL自定义函数(UDF)和标量函数(Scalar Function)...

14、Set 和 Map 数据结构
文章目录 14、Set 和 Map 数据结构1. Set1.1 基本用法☆☆☆ 值唯一,没有重复的值☆☆☆ 接受数组、具有 iterable 接口的数据结构☆☆☆ 数组去重1:[...new Set(array)]☆☆☆ 字符串去重:[...new Set(ababbc)].join()☆ 两个对象总是不相等…...
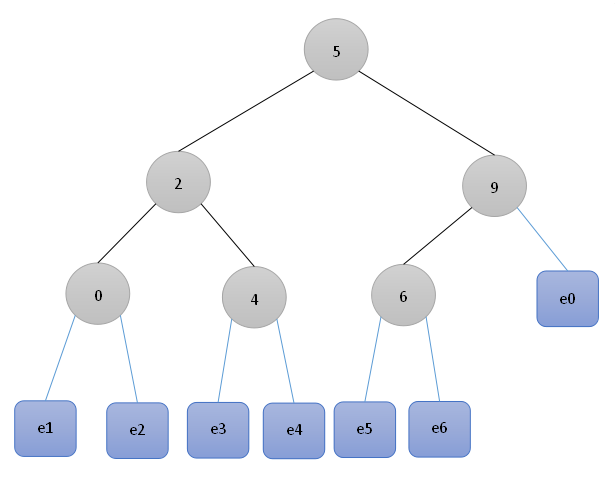
数据结构与算法设计分析——动态规划
目录 一、动态规划的定义二、动态规划的基本要素和主要步骤(一)最优子结构(二)重叠子问题 三、贪心法、分治法和动态规划的对比(一)贪心法(二)分治法(三)动态…...

PHPExcel 字母列不够用,针对 AA、AB、AC ... ZZ 这样的列
在PHPExcel 导出功能中,如果字段超过26个字母时,会出现字母不够用A~Z后 AA~AZ来添加后续字段 php中,chr() 函数从指定 ASCII 值返回字符,可以自定义一个方法来返回对应的字母 // $num 列数 1,2,3,4,5,6,7...... function getCol…...

fastdds源码编译安装
如何根据源码编译 fastdds 如何根据源码编译 fastdds 这里是为了根据源码编译一个 fastdds 。 fastdds 依赖 fastcdr Asio TinyXMl2 下载 fastdds 源码 git clone gitgithub.com:eProsima/Fast-DDS.git 进入 下载好的 fastdds 中执行 git submodule update --init --recurs…...
第二证券:风电概念强势拉升,威力传动“20cm”涨停,双一科技等大涨
风电概念20日盘中强势拉升,到发稿,威力传动“20cm”涨停,双一科技涨超17%,顺发恒业亦涨停,金雷股份、大金重工涨约7%,新强联、海力风电涨超5%。 音讯面上,9月以来江苏、广东海风项目加快推动&a…...

DataFrame窗口函数操作
文章最前: 我是Octopus,这个名字来源于我的中文名--章鱼;我热爱编程、热爱算法、热爱开源。所有源码在我的个人github ;这博客是记录我学习的点点滴滴,如果您对 Python、Java、AI、算法有兴趣,可以关注我的…...

【德哥说库系列】-RHEL8环境源码编译安装MySQL8.0
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...

Sandboxie+Buster Sandbox Analyzer打造个人沙箱
一、运行环境和需要安装的软件 实验环境:win7_x32或win7_x64 用到的软件:WinPcap_4_1_3.exe、Sandboxie-3-70.exe、Buster Sandbox Analyzer 重点是Sandboxie必须是3.70版本。下载地址:https://github.com/sandboxie-plus/sandboxie-old/blo…...

源码解析flink的GenericWriteAheadSink为什么做不到精确一次输出
背景 GenericWriteAheadSink是可以用于几乎是精准一次输出的场景,为什么说是几乎精准一次呢?我们从源码的角度分析一下 GenericWriteAheadSink做不到精准一次输出的原因 首先我们看一下flink检查点完成后通知GenericWriteAheadSink开始进行分段的记录…...
)
C#经典十大排序算法(完结)
C#冒泡排序算法 简介 冒泡排序算法是一种基础的排序算法,它的实现原理比较简单。核心思想是通过相邻元素的比较和交换来将最大(或最小)的元素逐步"冒泡"到数列的末尾。 详细文章描述 https://mp.weixin.qq.com/s/z_LPZ6QUFNJcw…...

C/C++文件操作(细节满满,part2)
该文章上一篇:C/C文件操作(细节满满,part1)_仍有未知等待探索的博客-CSDN博客 个人主页:仍有未知等待探索_C语言疑难,数据结构,小项目-CSDN博客 专题分栏:C语言疑难_仍有未知等待探索的博客-CSDN博客 目录 …...
web前端面试-- 手写原生Javascript方法(new、Object.create)
web面试题 本人是一个web前端开发工程师,主要是vue框架,整理了一些面试题,今后也会一直更新,有好题目的同学欢迎评论区分享 ;-) web面试题专栏:点击此处 手动实现Object.create 通过Object.create&#…...

C++前缀和算法的应用:得到连续 K 个 1 的最少相邻交换次数 原理源码测试用例
本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 滑动窗口 题目 给你一个整数数组 nums 和一个整数 k 。 nums 仅包含 0 和 1 。每一次移动,你可以选择 相邻 两个数字并将它们交换。 请你返回使 nums 中包…...

目标检测YOLO实战应用案例100讲-基于YOLOv5的航拍图像旋转目标检测
目录 前言 国内外研究历史与现状 目标检测技术的研究历史与现状...
H5前端开发——BOM
H5前端开发——BOM BOM(Browser Object Model)是指浏览器对象模型,它提供了一组对象和方法,用于与浏览器窗口进行交互。 通过 BOM 对象,开发人员可以操作浏览器窗口的行为和状态,实现与用户的交互和数据传…...

stable diffusion如何解决gradio外链无法开启的问题
问题确认 为了确认gradio开启不了是gradio库的问题还是stable diffusion的问题,可以先执行这样一段demo代码 import gradio as grdef greet(name):return "Hello " name "!"demo gr.Interface(fngreet, inputs"text", outputs&q…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
