数据结构与算法设计分析——动态规划
目录
- 一、动态规划的定义
- 二、动态规划的基本要素和主要步骤
- (一)最优子结构
- (二)重叠子问题
- 三、贪心法、分治法和动态规划的对比
- (一)贪心法
- (二)分治法
- (三)动态规划
- 四、动态规划的递归和迭代法求解
- (一)由顶向下的递归法
- (二)由底向上的迭代法
- 五、动态规划的应用
- (一)斐波那契数列
- (二)汉诺塔
- (三)最优二叉查找树
- (四)矩阵连乘
- (五)0-1背包
一、动态规划的定义
动态规划的基本思想是将问题分成若干个子问题,先求解子问题,然后从子问题的解进而得到原问题的解。
二、动态规划的基本要素和主要步骤
动态规划算法的两个基本要素是最优子结构和重叠子问题,其主要步骤如下:
①问题需要具有最优子结构性质;
②构造最优值的递归表达式;
③最优值的算法描述;
④构造最优解。
(一)最优子结构
问题可分为若干个子问题,最优子结构指的是问题的最优解可以由其子问题的最优解求解出来,它的也是依据将复杂问题分解成简单子问题的方法。总的来说,某一问题可用动态规划算法求解的显著特征是该问题具有最优子结构性质。
(二)重叠子问题
当划分的子问题中有些子问题重复出现时,这些问题是会被重复计算和求解的,从而会导致算法效率低且造成空间开销,而动态规划的优势在求解划分的重叠子问题的时候,将第一次求解的解通过数组或表存储起来,从而可以避免重复计算后面相同的子问题。
三、贪心法、分治法和动态规划的对比
(一)贪心法
每一步都选择当前最优解,而不考虑该决策对整体的影响。贪心算法通常适用于简单、容易分解的问题,即具有贪心选择性质和最优子结构两个重要的性质的问题求解。贪心法总是做出最好的选择,可以快速地得到近似上的最优解的情况(局部最优选择),时间复杂度较低,但其缺点是不能保证得到全局上的最优解。
(二)分治法
可分为分解、治理两大步骤,其通常适用于优化问题,采用递归的思想,每次将问题分成两个或更多的小问题,由于各个子问题是相互独立的,所以通过递归最终合并可以很容易得到原问题的解,但若各个子问题不是相互独立的时,则会造成重复,从而会有很高的时间复杂度。
(三)动态规划
与分治法不同的是,动态规划通常解决的是重叠子问题性质和最优子结构性质的问题,其中解决子问题只需一次,解决后会将其解保存并重复使用,避免重复计算。动态规划通常采用自底向上的方式,通过先解决子问题,再解决大问题的方式进行求解。动态规划适合用于优化问题,并且能够保证得到全局最优解。但对比贪心法、分治法算法,由于需要存储各种状态,所以其需要的空间更大。
三种算法的对比如下表:
| 名称 | 贪心法 | 分治法 | 动态规划 |
|---|---|---|---|
| 适用性 | 一般问题 | 优化问题 | 优化问题 |
| 求解 | 线性求解 | 递归求解 | 递归和迭代求解 |
| 求解顺序 | 先选择后解决子问题 | 先选择后解决子问题 | 先解决子问题后选择 |
| 特征 | 由顶向下 | 由顶向下 | 由顶向下、由底向上 |
| 最优子结构 | 满足 | 不满足 | 满足 |
| 子问题规模 | 仅一个子问题 | 所有子问题 | 所有子问题 |
| 子问题独立性 | 仅一个子问题 | 每个子问题独立 | 每个子问题重叠不独立 |
| 子问题最优解 | 部分最优解 | 全部最优解 | 部分最优解 |
四、动态规划的递归和迭代法求解
(一)由顶向下的递归法
由顶向下的递归法也被称为带记忆的由顶向下法,可概括为递归+可记忆,是一种自上而下的分治思想,一开始将问题分成子问题,通过递归先解决子问题,这里的可记忆指的是保存每个子问题的解,这些解被保存到一个数组或表格中,其目的是为了避免重复计算,节省时间。该方法通常由递归函数实现,同时,结合记忆化可以消除重复计算,从而大幅度提升计算效率,缩短时间。
(二)由底向上的迭代法
由底向上的迭代方法可概括为迭代+动态规划,是一种自下而上的构建思想。通过将问题分成相互独立、可简单直接求解的子问题,并将子问题的解按由小到大的顺序保存下来,逐步构建出问题的最优解,即当求解某个子问题时,其所依赖的更小的子问题已经是求解了的,从而每个子问题只需求解一次即可。该方法通常由循环语句实现,可以避免采用递归函数时所带来的额外开销。
以上两种方法具有相同的渐进运行时间,仅有的差异是在某些特殊情况下,由顶向下方法并未真正递归地考察所有可能的子问题。由于没有频繁的递归函数调用的开销,由底向上方法的时间复杂性函数通常具有更小的系数。
五、动态规划的应用
(一)斐波那契数列
由斐波那契数列(Fibonacci),可得
递归关系式:F(n) = F(n-1) + F(n-2) ,
其中F(0)=0,F(1) = F(2) = 1。
f(n)的求解可以类比一棵二叉树,以F(5)为例,根据递归关系式可画出二叉树,如下图:
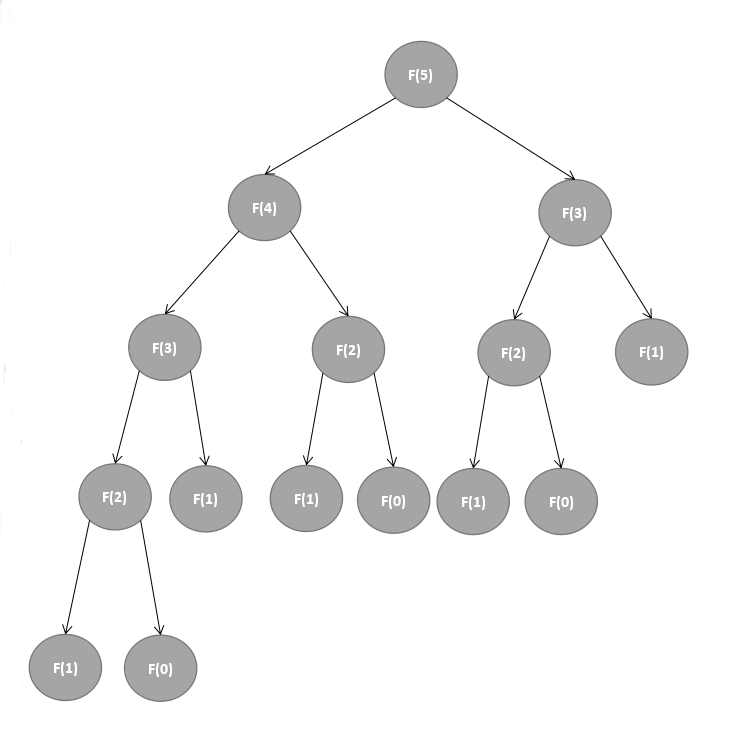
1、若采用不带记忆的由顶向下的递归法时,其中有重复的子问题,会造成重复计算,从而加大开销,且当计算的n值越来越大时,空间开销会更大。
所以,采用带记忆的由顶向下的递归法,通过建立一个一维数组来保存每个子问题的解,当计算时,只需从数组中取出相应的值即可,从而可以避免重复计算【避免子问题重叠】。这种方法只需求需要的相应值即可,该树中,有重复的子问题如下:

创建一个数组,首先将F(0)、F(1)和F(2)的解存在数组中,如下:
| F(0) | F(1) | F(2) | ||
|---|---|---|---|---|
| 数组 | 0 | 1 | 1 |
求解F(3)时,根据递归关系式,F(n) = F(n-1) + F(n-2) ,即F(3) = F(2) + F(1) =1+1=2,直接取数组中F(2)和F(1)的值代入计算即可,然后将F(3)存放在数组中,如下:
| F(0) | F(1) | F(2) | F(3) | ||
|---|---|---|---|---|---|
| 数组 | 0 | 1 | 1 | 2 |
求解F(4)时,根据递归关系式,F(n) = F(n-1) + F(n-2) ,即F(4) = F(3) + F(2) =2+1=3,直接取数组中F(3)和F(2)的值代入计算即可,然后将F(4)存放在数组中,如下:
| F(0) | F(1) | F(2) | F(3) | F(4) | ||
|---|---|---|---|---|---|---|
| 数组 | 0 | 1 | 1 | 2 | 3 |
……依次最终求得F(5)=F(4) + F(3)=3+2=5:
| F(0) | F(1) | F(2) | F(3) | F(4) | F(5) | ||
|---|---|---|---|---|---|---|---|
| 数组 | 0 | 1 | 1 | 2 | 3 | 5 |
2、若采用由底向上的迭代方法,自下而上的构建,通常由循环语句实现,可以避免采用递归函数时所带来的额外开销,如下代码,通过for()循环实现:
#include <stdio.h>
int main()
{int i, n;long long int f1 = 1, f2 = 1, f; //初始值f1=f2=1printf("请输入要输出的斐波那契数列项数:");scanf("%d", &n);printf("斐波那契数列前%d项为:\n", n);printf("%lld %lld ", f1, f2);for (i = 3; i <= n; i++){f = f1 + f2;printf("%lld ", f);f1 = f2;f2 = f;}printf("\n");return 0;
}
(二)汉诺塔
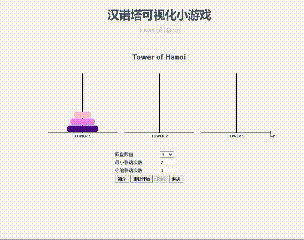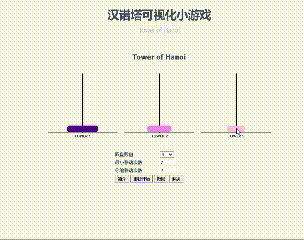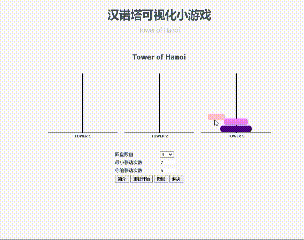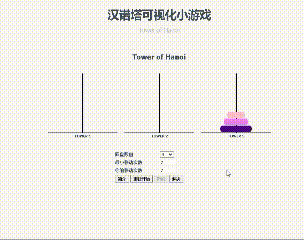
首先,这里简单地以一个三层的汉诺塔,熟悉一下汉诺塔的游戏规则:一共有三根柱子,第一根柱子上有三个从上到下由小到大的圆盘,规定每次在三根柱子之间一次只能移动一个圆盘,且小圆盘上不能放大圆盘,试将第一根的三个圆盘移动到第三根柱子上。
点击链接可以试试,怎么让移动的次数最少?
汉诺塔可视化小游戏 Tower of Hanoi
最终的目的是完成的步数越少越好,我们可以很容易地得到三层的汉诺塔的最少移动步数为7次,移动过程中三个柱子共有8种不同的状态,如下:
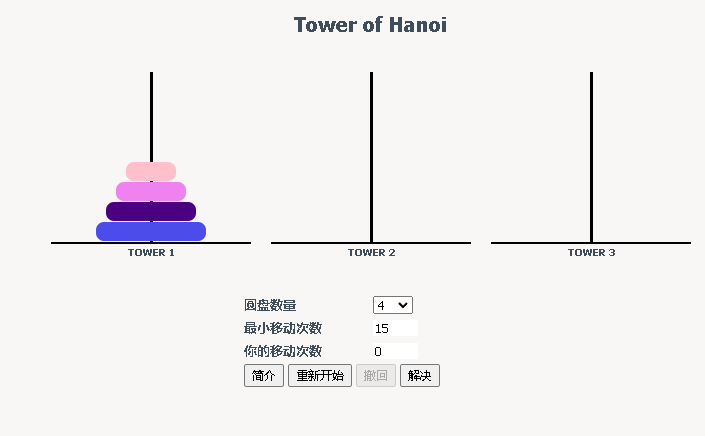
同样的,四层的汉诺塔的最少移动步数为15次,而移动过程中三个柱子共有16种不同的状态:
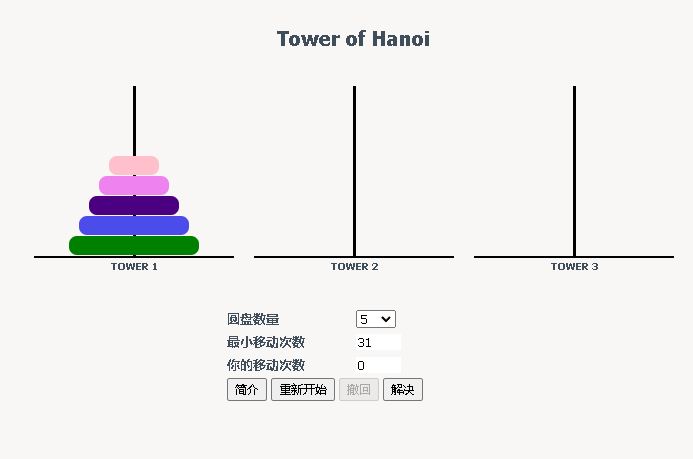
五层的汉诺塔的最少移动步数为31次,而移动过程中三个柱子共有32种不同的状态:
……
通过数学归纳法,可得,当汉诺塔的层数为n时,最少的移动次数为 2n-1次,移动过程中三个柱子共有2n 种不同的状态,其时间复杂度为O(2n) 。
- 汉诺塔问题的动态规划优化问题是通过带记忆的由顶向下法求解,即递归+可记忆,先解决小的问题,然后将问题的规模从小到大逐步扩大,最终得到问题的答案,且过程中避免了重复计算。【
避免子问题重叠】
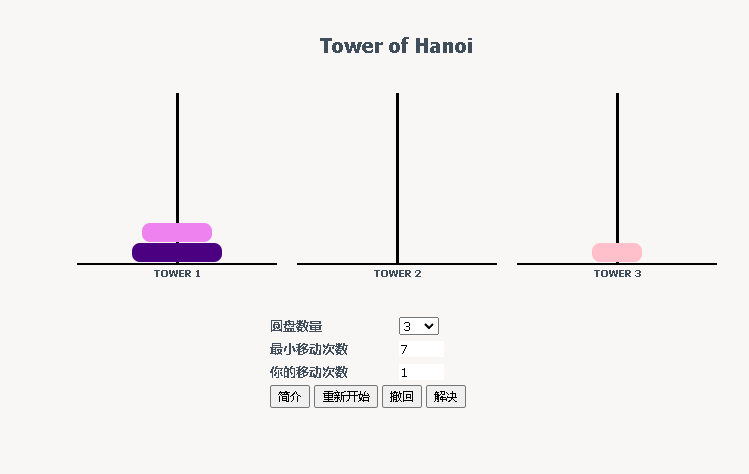
若以f[ n ]表示n个圆盘从TOWER 1移动到TOWER 3的最少步数,则f[1] = 1,即一个圆盘移动到TOWER 3的步数为1,而当n>1时,分析可知:
为了符合规则,需要先将一部分移动到TOWER 2上面,即有n-1个圆盘从TOWER 1经TOWER 3移动到TOWER 2上面,然后再将最大的圆盘移动到TOWER 3上面,由于TOWER 2已经是有序的,所以,需要将这n-1个圆盘从TOWER 2移动到TOWER 1,最终再移动到TOWER 3上。
可得,n个圆盘从TOWER 1移动到TOWER 3的最少步数为f[ n ]=f (n -1) + 1 + f (n - 1)=2f (n - 1)+1= 2n-1+1,即T(n)= 2n-1+1,所以时间复杂度为O(2n) 。
也可以从圆盘的数量来计算,按照规则,一个圆盘从TOWER 1移动到TOWER 3需要1步,两个圆盘从TOWER 1移动到TOWER 3需要3步(小的圆盘移动到中转点,再将大的圆盘移动到终点,最后将小的圆盘移动到终点),三个圆盘从TOWER 1移动到TOWER 3需要7步,……,n个圆盘从TOWER 1移动到TOWER 3需要3步 2n-1步。
(三)最优二叉查找树
1、最优二叉查找树的定义
在n个不同关键字组成的有序序列中,每个关键字被查找的概率为pi,通过关键字构造一棵的二叉查找树,它具有最小平均比较次数,即为最优二叉查找树(OBST),且左右子树也是最优二叉查找树,但最优二叉查找树不一定是高度最小的二叉查找树。
2、二叉查找树平均比较次数的计算
设有n=6个关键字的集合,各个实结点的查找概率分别为5:5%、2:30%、9:10%、0:3%、4:14%、6:25%,假设虚结点的查找概率分别为:e0:2%、e1:10%、e2:5%、e3:5%、e4:11%、e5:15%、e6:10%,计算二叉查找树的平均比较次数:
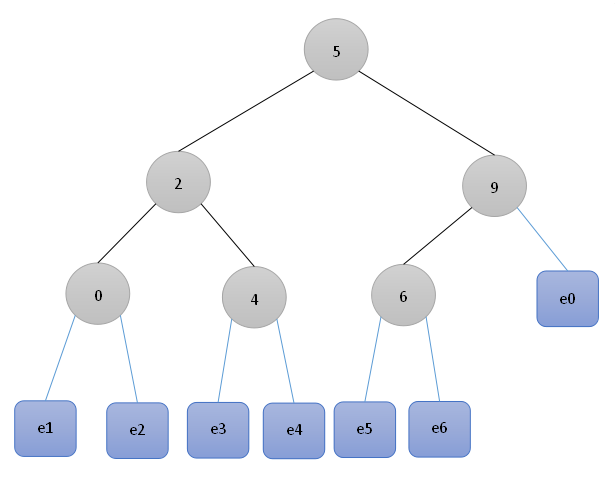
实结点:1×0.05+2×(0.3+0.1)+3×(0.03+0.14+0.25)=2.11;
虚结点:2×0.02+3×(0.1+0.05+0.05+0.11+0.15+0.1)=1.72,
即二叉查找树的平均比较次数为2.11+1.72=3.83。
3、最优子结构
最优二叉查找树中采用了动态规划的思想,分析其最优子结构:若一个二叉查找树是最优二叉查找树,可将其分为根结点、左子树和右子树,所以其左、右子树也是最优二叉查找树。
4、构建最优二叉查找树的分析
构建一个含n个关键字的最优二叉查找树的时间复杂度为O(n3),由于通过使用二维数组,避免重复计算子树的最小权值和【避免子问题重叠】,从而提高了算法的效率,其空间复杂度为O(n2)。
(四)矩阵连乘
问题描述:在《线性代数》里面,学过矩阵的乘法,若干个矩阵相乘时,由于满足结合律,即(AB)C = A (BC),可以通过加括号可以改变乘积的顺序,而结果不改变。若从相乘的计算量上来看,怎么让计算所需要的代价最少,即怎么通过加括号(改变乘积顺序),来使计算量最小,这是通过动态规划来优化问题的所在。
- 可将问题划分成两个子问题,即两个部分的矩阵相乘,分别对两个子问题进行递归求解,通过定义一个二维数组C[i][j]来表示第i个矩阵到第j个矩阵相乘的最小代价,以分界点k分割问题,对于两个子问题可分别表示为C[i][k]和C[k+1][j],然后通过相同的方法继续进行递归求解,由于第i个矩阵的行数在p[i-1],其列数在p[i],所以递归式为C[i][j]=C[i][k]+C[k+1][j]+p[i-1]×p[k]×p[j],该算法的时间复杂度取决于对所有矩阵求优解,即递归式上花费的时间,时间复杂度为O(n3)。
(五)0-1背包
问题描述:有n件物品,对某一物品i,其价值为V,重量为W,怎么选择将物品放入背包中,使得放入背包的物品的总价值最大,而动态规划就是来优化这个问题。
- 通过一个数组C[i][j]表示i个物品放入背包,此时背包容量为j所能得到的最大价值,由于当每个物品放入背包时,都要两种情况,能放进背包的要求是其所占重量要小于或等于当前背包剩余容量,即此时总价值为C[i-1][j-wi]+vi;不能放进背包的情况时,此时总价值为C[i-1][j],然后通过这两种状态取最大值,即C[i][j]=Max{C[i-1][j],C[i-1][j-wi]+vi}。由于得到的是背包的最大价值,设i=n、j=W,再通过一开始的最优解C[n][W]的值反推,确定放入背包的相应物品,即实现放入背包物品价值最大化,该算法的时间复杂度取决于物品个数n的一个for()循环语句和物品的重量W的一个for()循环语句,故其时间复杂度为O(nW)。
相关文章:

数据结构与算法设计分析——动态规划
目录 一、动态规划的定义二、动态规划的基本要素和主要步骤(一)最优子结构(二)重叠子问题 三、贪心法、分治法和动态规划的对比(一)贪心法(二)分治法(三)动态…...

PHPExcel 字母列不够用,针对 AA、AB、AC ... ZZ 这样的列
在PHPExcel 导出功能中,如果字段超过26个字母时,会出现字母不够用A~Z后 AA~AZ来添加后续字段 php中,chr() 函数从指定 ASCII 值返回字符,可以自定义一个方法来返回对应的字母 // $num 列数 1,2,3,4,5,6,7...... function getCol…...

fastdds源码编译安装
如何根据源码编译 fastdds 如何根据源码编译 fastdds 这里是为了根据源码编译一个 fastdds 。 fastdds 依赖 fastcdr Asio TinyXMl2 下载 fastdds 源码 git clone gitgithub.com:eProsima/Fast-DDS.git 进入 下载好的 fastdds 中执行 git submodule update --init --recurs…...
第二证券:风电概念强势拉升,威力传动“20cm”涨停,双一科技等大涨
风电概念20日盘中强势拉升,到发稿,威力传动“20cm”涨停,双一科技涨超17%,顺发恒业亦涨停,金雷股份、大金重工涨约7%,新强联、海力风电涨超5%。 音讯面上,9月以来江苏、广东海风项目加快推动&a…...

DataFrame窗口函数操作
文章最前: 我是Octopus,这个名字来源于我的中文名--章鱼;我热爱编程、热爱算法、热爱开源。所有源码在我的个人github ;这博客是记录我学习的点点滴滴,如果您对 Python、Java、AI、算法有兴趣,可以关注我的…...

【德哥说库系列】-RHEL8环境源码编译安装MySQL8.0
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...

Sandboxie+Buster Sandbox Analyzer打造个人沙箱
一、运行环境和需要安装的软件 实验环境:win7_x32或win7_x64 用到的软件:WinPcap_4_1_3.exe、Sandboxie-3-70.exe、Buster Sandbox Analyzer 重点是Sandboxie必须是3.70版本。下载地址:https://github.com/sandboxie-plus/sandboxie-old/blo…...

源码解析flink的GenericWriteAheadSink为什么做不到精确一次输出
背景 GenericWriteAheadSink是可以用于几乎是精准一次输出的场景,为什么说是几乎精准一次呢?我们从源码的角度分析一下 GenericWriteAheadSink做不到精准一次输出的原因 首先我们看一下flink检查点完成后通知GenericWriteAheadSink开始进行分段的记录…...
)
C#经典十大排序算法(完结)
C#冒泡排序算法 简介 冒泡排序算法是一种基础的排序算法,它的实现原理比较简单。核心思想是通过相邻元素的比较和交换来将最大(或最小)的元素逐步"冒泡"到数列的末尾。 详细文章描述 https://mp.weixin.qq.com/s/z_LPZ6QUFNJcw…...

C/C++文件操作(细节满满,part2)
该文章上一篇:C/C文件操作(细节满满,part1)_仍有未知等待探索的博客-CSDN博客 个人主页:仍有未知等待探索_C语言疑难,数据结构,小项目-CSDN博客 专题分栏:C语言疑难_仍有未知等待探索的博客-CSDN博客 目录 …...
web前端面试-- 手写原生Javascript方法(new、Object.create)
web面试题 本人是一个web前端开发工程师,主要是vue框架,整理了一些面试题,今后也会一直更新,有好题目的同学欢迎评论区分享 ;-) web面试题专栏:点击此处 手动实现Object.create 通过Object.create&#…...

C++前缀和算法的应用:得到连续 K 个 1 的最少相邻交换次数 原理源码测试用例
本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 滑动窗口 题目 给你一个整数数组 nums 和一个整数 k 。 nums 仅包含 0 和 1 。每一次移动,你可以选择 相邻 两个数字并将它们交换。 请你返回使 nums 中包…...

目标检测YOLO实战应用案例100讲-基于YOLOv5的航拍图像旋转目标检测
目录 前言 国内外研究历史与现状 目标检测技术的研究历史与现状...
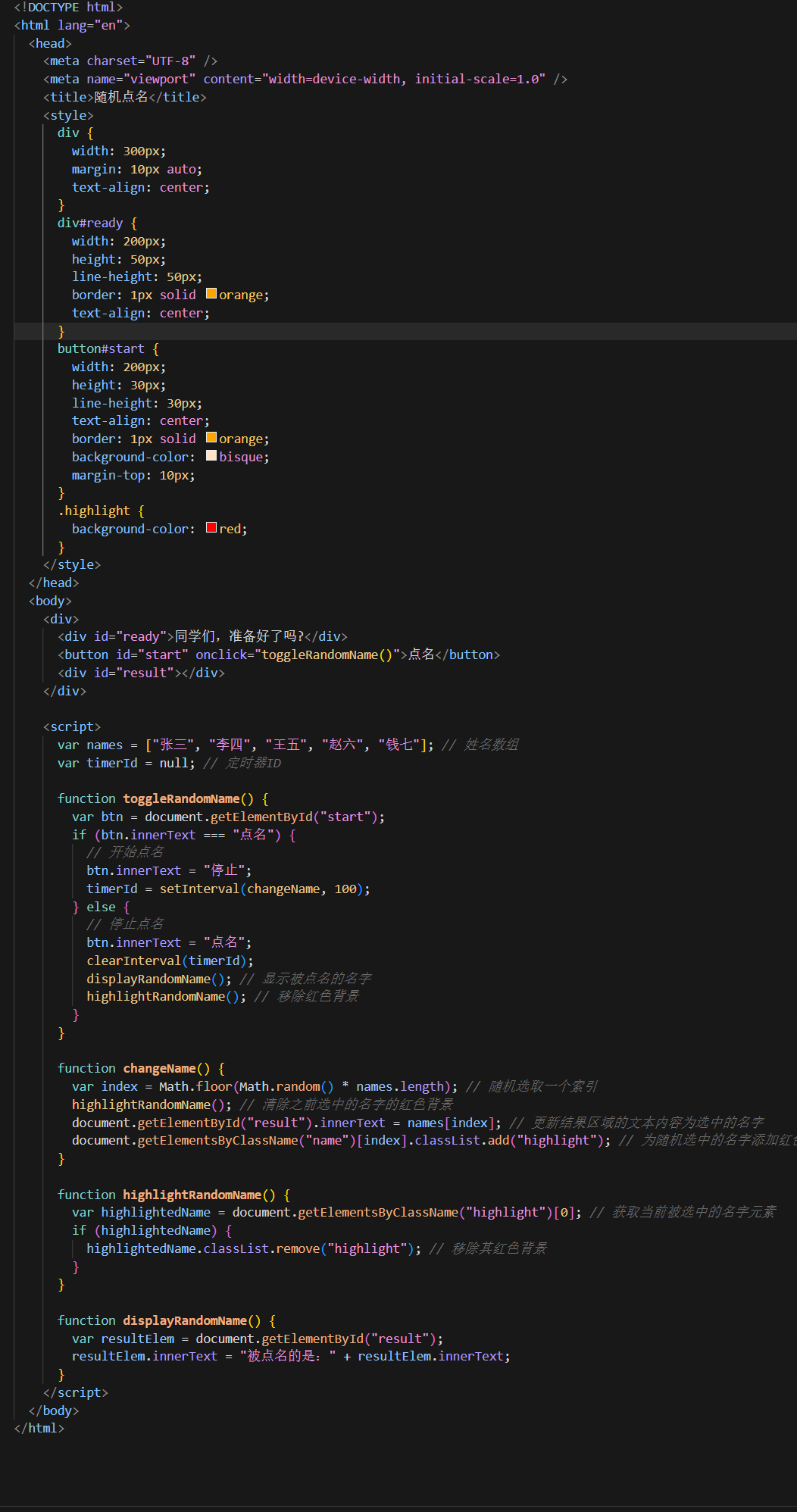
H5前端开发——BOM
H5前端开发——BOM BOM(Browser Object Model)是指浏览器对象模型,它提供了一组对象和方法,用于与浏览器窗口进行交互。 通过 BOM 对象,开发人员可以操作浏览器窗口的行为和状态,实现与用户的交互和数据传…...

stable diffusion如何解决gradio外链无法开启的问题
问题确认 为了确认gradio开启不了是gradio库的问题还是stable diffusion的问题,可以先执行这样一段demo代码 import gradio as grdef greet(name):return "Hello " name "!"demo gr.Interface(fngreet, inputs"text", outputs&q…...

SpringMvc-面试用
一、SpringMvc常用注解 1、修饰在类的 RestController RequestMapping("/test")RestController是什么?其实是一个复合注解 Controller //其实就是Component ResponseBody //独立的注解 public interface RestController {}RequestMapping 也可以认…...

并发编程 # 3
文章目录 一、进程和线程的比较二、GIL全局解释器锁1.引入2.Python解释器的种类结论:在CPython解释其中,同一个进程下开启的多线程,同一时刻只能有一个线程执行,无法利用多核优势。得出结论:GIL锁就是保证在同一时刻只…...

ESP32C3 LuatOS TM1650①驱动测试
合宙TM1650驱动资料 TM1650.lua源码 引脚连接 TM1650ESP32C3SCLGPIO5SDAGPIO4 下载TM1650.lua源码,并以文件形式保存在项目文件夹中 驱动测试源码 --注意:因使用了sys.wait()所有api需要在协程中使用 -- 用法实例 PROJECT "ESP32C3_TM1650" VERSION …...

TCP为什么需要三次握手和四次挥手?
一、三次握手 三次握手(Three-way Handshake)其实就是指建立一个TCP连接时,需要客户端和服务器总共发送3个包 主要作用就是为了确认双方的接收能力和发送能力是否正常、指定自己的初始化序列号为后面的可靠性传送做准备 过程如下ÿ…...
【C++】一些C++11特性
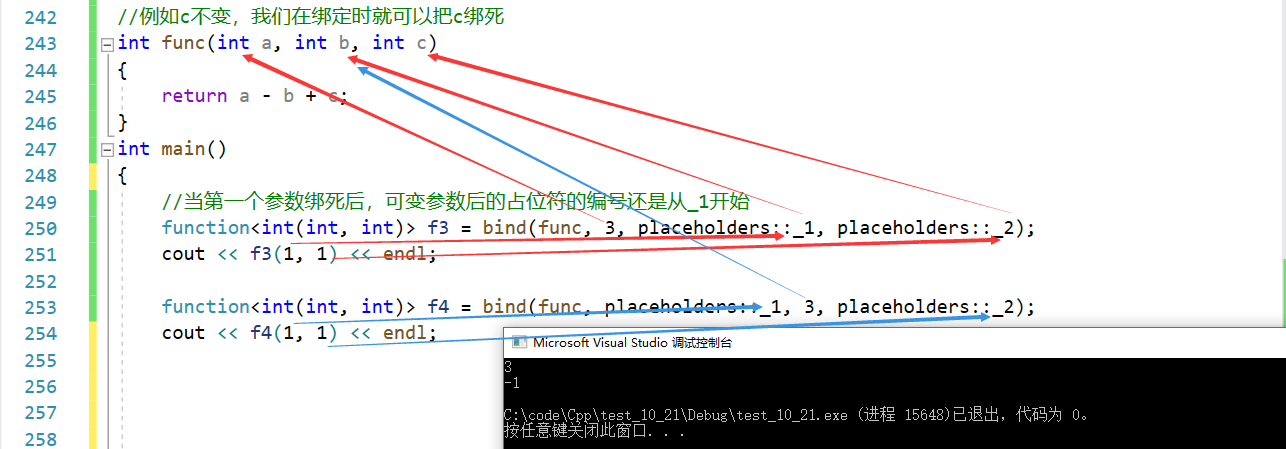
C特性 1. 列表初始化1.1 {}初始化1.2 initializer_list 2. 声明2.1 auto2.2 typeid2.3 decltype2.4 nullptr 3. STL3.1 新容器3.2 新接口 4. 右值引用5. 移动构造与移动赋值6. lambda表达式7. 可变参数模板8. 包装器9. bind 1. 列表初始化 1.1 {}初始化 C11支持所有内置类型和…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
