泰森多边形
泰森多边形
93
泰森多边形又叫沃洛诺伊图(Voronoi diagram),得名于Georgy Voronoi,是一组由连接两邻点线段的垂直平分线组成的连续多边形。一个泰森多边形内的任一点到构成该多边形的控制点的距离小于到其他多边形控制点的距离。
中文名泰森多边形外文名Thiessen Polygon性 质多边形概 念泰森多边形内的点到相应离散点的距离最近,且每个泰森多边形仅有一个离散点。发明者荷兰气候学家A·H·Thiessen
目录
1 简介
2 数学描述
3 建立步骤
4 特征
5 泰森多边形面积
6 作用
简介编辑 播报
泰森多边形是对空间平面的一种剖分,其特点是多边形内的任何位置离该多边形的样点(如居民点)的距离最近,离相邻多边形内样点的距离远,且每个多边形内含且仅包含一个样点。由于泰森多边形在空间剖分上的等分性特征,因此可用于解决最近点、最小封闭圆等问题,以及许多空间分析问题,如邻接、接近度和可达性分析等。
数学描述编辑 播报
[1] 设平面区域B上有一组离散点 (i = 1,2,3,…,k ; j = 1,2,3,…,k ,k为离散点点数),若将区域B用一组直线段分成k个互相邻接的多边形,使得:
(1)每个多边形内含有且仅含有一个离散点;
(2)若区域B 上任意一点 位于含离散点 的多边形内,不等式 (1)
在 时恒成立;
(3)若点 位于含离散点 的两个多边形的公共边上,则等式 (2)
成立。
由此得到的多边形叫泰森多边形。用直线连接每两个相邻多边形内的离散点形成的三角形叫泰森三角形。
建立步骤编辑 播报
泰森多边形的建立:
建立泰森多边形算法的关键是对离散数据点合理地连成三角网,即构建Delaunay三角网。建立泰森多边形的步骤为:
1、离散点自动构建三角网,即构建Delaunay三角网。对离散点和形成的三角形编号,记录每个三角形是由哪三个离散点构成的。
2、找出与每个离散点相邻的所有三角形的编号,并记录下来。这只要在已构建的三角网中找出具有一个相同顶点的所有三角形即可。
3、对与每个离散点相邻的三角形按顺时针或逆时针方向排序,以便下一步连接生成泰森多边形。设离散点为o。找出以o为顶点的一个三角形,设为A;取三角形A除o以外的另一顶点,设为a,则另一个顶点也可找出,即为f;则下一个三角形必然是以of为边的,即为三角形F;三角形F的另一顶点为e,则下一三角形是以oe为边的;如此重复进行,直到回到oa边。
4、计算每个三角形的外接圆圆心,并记录之。
5、根据每个离散点的相邻三角形,连接这些相邻三角形的外接圆圆心,即得到泰森多边形。对于三角网边缘的泰森多边形,可作垂直平分线与图廓相交,与图廓一起构成泰森多边形。 [2]
特征编辑 播报
1、每个泰森多边形内仅含有一个离散点数据;
2、泰森多边形内的点到相应离散点的距离最近;
3、位于泰森多边形边上的点到其两边的离散点的距离相等。
泰森多边形面积编辑 播报
由于泰森多边形面积随点集的分布而发生变化,因此可用多边形面积的变异系数CV值(即泰森多边形面积的标准差与平均值的比)来衡量凸多边形面积的变化程度,从而评估样点的分布类型。
CV值公式见式(1)、式(2):
式(1):
式(2):
CV=
式中,Si是第i个多边形的面积,S为多边形面积的平均值,n是多边形面积的个数,R为方差.当点集分布类型为“均匀”时,多边形面积变化小,CV值就小,当点集为“集群”分布时,集群内的多边形面积较小,而集群间的多边形面积较大,CV值也大.Duyckaert提出了三个建议值:当点集为“随机分布”时,CV=57 %(包括33%.–64% ) ;当点集为“集群”分布时,CV=92%(包括>64% );当点集为“均匀分布”时,CV=29%(包括<<33% )。要注意的是,位于边缘上的点的泰森多边形面积直接受到人为划定边界的影响,边界越大,边缘点的泰森多边形面积也越大,反之边缘点的泰森多边形面积越小,所以在计算泰森多边形面积的CV值时,要考虑边界的影响。 [1]
作用编辑 播报
泰森多边形可用于定性分析、统计分析、邻近分析等。
例如,可以用离散点的性质来描述泰森多边形区域的性质;可用离散点的数据来计算泰森多边形区域的数据;判断一个离散点与其它哪些离散点相邻时,可根据泰森多边形直接得出,且若泰森多边形是n边形,则就与n个离散点相邻;当某一数据点落入某一泰森多边形中时,它与相应的离散点最邻近,无需计算距离。
在泰森多边形的构建中,首先要将离散点构成三角网。这种三角网称为Delaunay三角网。北京奥运会的水立方即是基于此原理设计。
相关文章:

泰森多边形
泰森多边形 93 泰森多边形又叫沃洛诺伊图(Voronoi diagram),得名于Georgy Voronoi,是一组由连接两邻点线段的垂直平分线组成的连续多边形。一个泰森多边形内的任一点到构成该多边形的控制点的距离小于到其他多边形控制点的距离。…...

YOLOV8 进行docker环境配置
修改docker文件 原docekerfile中ADD https://ultralytics.com/assets/Arial.ttf https://ultralytics.com/assets/Arial.Unicode.ttf /root/.config/Ultralytics/下载很慢,可以在外部下载好,放入docker文件夹中,再将源代码改为ADD Arial.ttf…...
)
sealos一键部署K8S环境(sealos3.0时代教程过时了,目前已经4.0了,请移步使用Sealos一键安装K8S)
1 安装Sealos(4.0版本) sealos部署k8s贼方便,只需要一条init命令即可,3分钟部署完(下载安装包的时间不算)。 官方教程:https://www.sealyun.com/instructions/1st #主机名: hostnamectl set-hostname mas…...
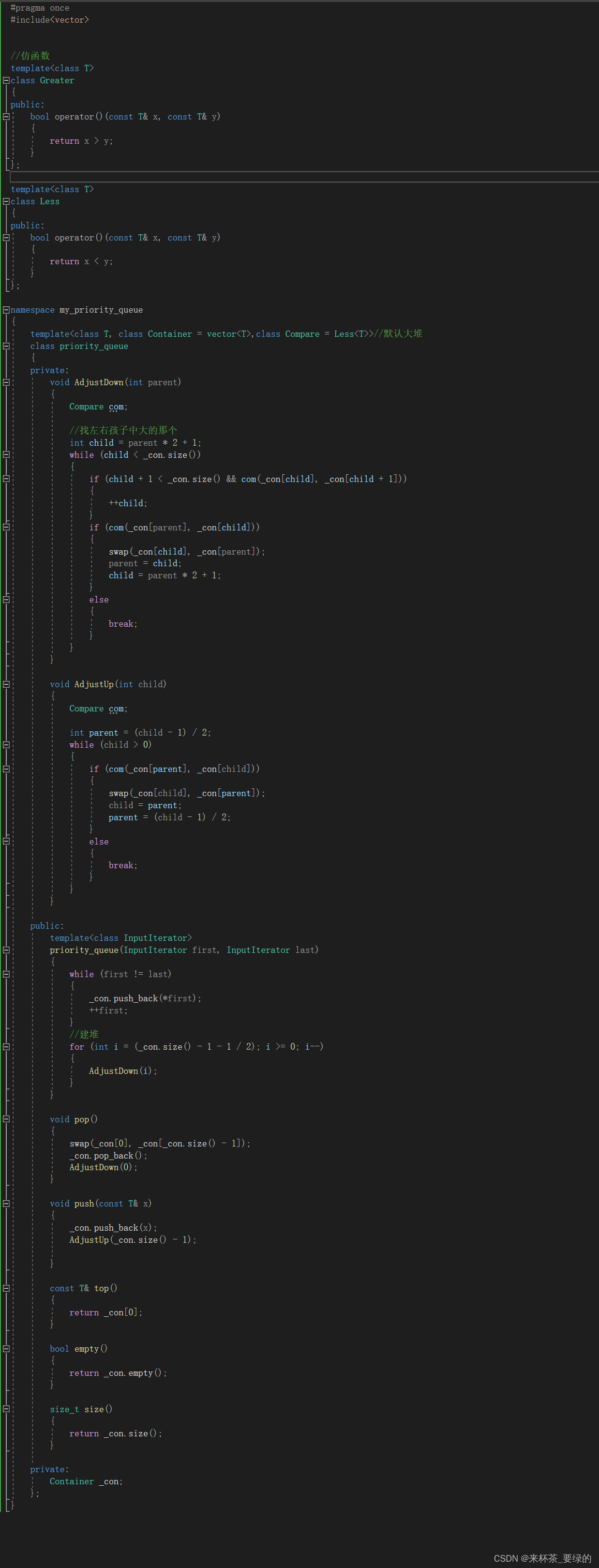
【C++】stackqueue
适配器是一种设计模式 , 该种模式是将一个类的接口转换成客户希望的另外一个接口 。 虽然 stack 和 queue 中也可以存放元素,但在 STL 中并没有将其划分在容器的行列,而是将其称为 容器适配 器 ,这是因为 stack 和队列只是对其他容…...

Hive篇面试题+详解
Hive篇面试题 1.什么是Hive?它的主要功能是什么? Hive是一个基于Hadoop的数据仓库工具,它提供了一个类SQL的查询语言(HiveQL)来查询和分析存储在Hadoop集群中的大规模数据。Hive的主要功能是将结构化数据映射到Hadoop…...

Mysql批量插入更新如何拆分大事务?
拆分大事务 一、解决方案二、遇到问题之前在运行Mysql任务的时候报错:binlog(1610646347 bytes) write threshold exceeded,原因是Mysql任务提交的是个大事务,超出binlog设定阈值,使得系统自动终止事务 一、解决方案 使用limit分页拆分大事务 CREATE PROCEDURE `split_tran…...
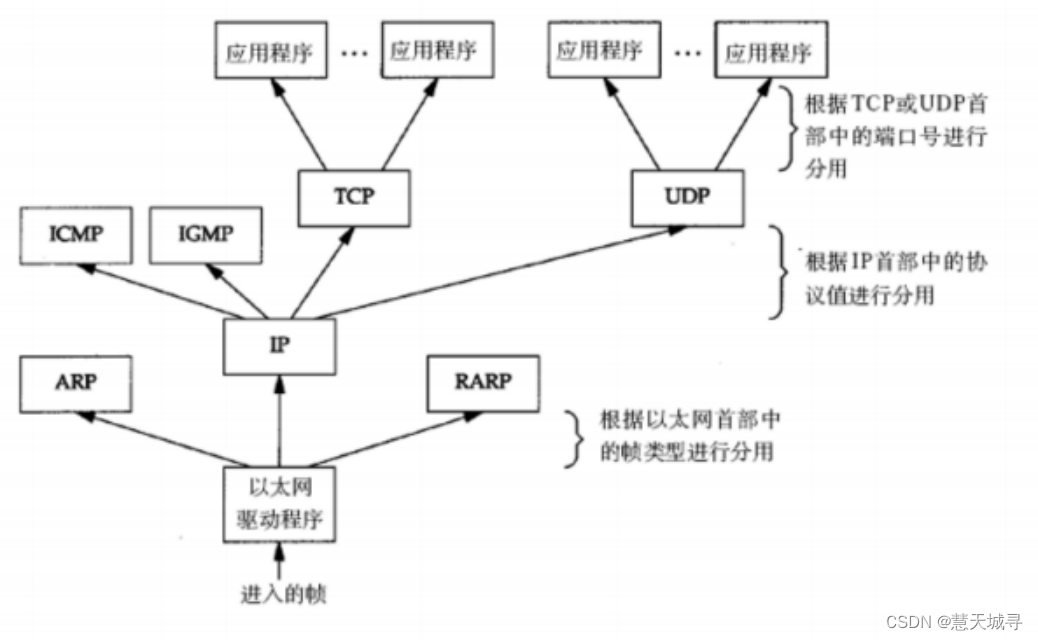
【计算机网络原理】初始网络基础
文章目录 1. 网络发展史1.1 单机时代1.2 网络互连局域网 LAN广域网 WAN 2. 网络通信基础2.1 IP 地址2.2 端口号2.3 协议2.4 五元组2.5 协议分层2.5.1 OSI七层模型2.5.2 TCP/IP五层模型 2.6 封装和分用2.6.1 数据封装(发送方情况)2.6.2 数据分用(接收方情况) 总结 1. 网络发展史…...
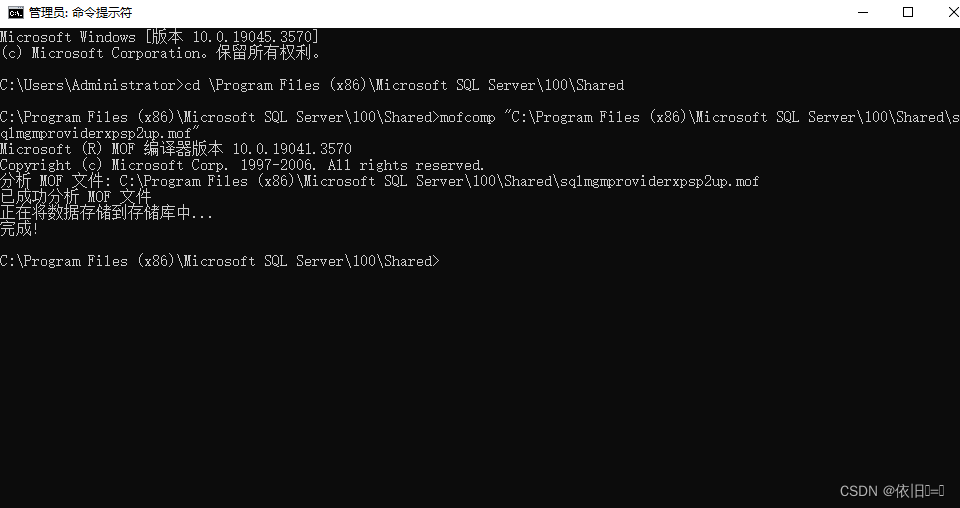
【sqlserver】配置管理器打不开
问题描述 无法连接到 WMI 提供程序。您没有权限或者该服务器无法访问。请注意,您只能使用SQL Server 配置管理器来管理 SQL Server 2005 和更高版本的服务 器。无效类[0x80041010] 解决方式: 命令提示符-右键-以管理员身份运行,再把以下代码执行一遍&…...
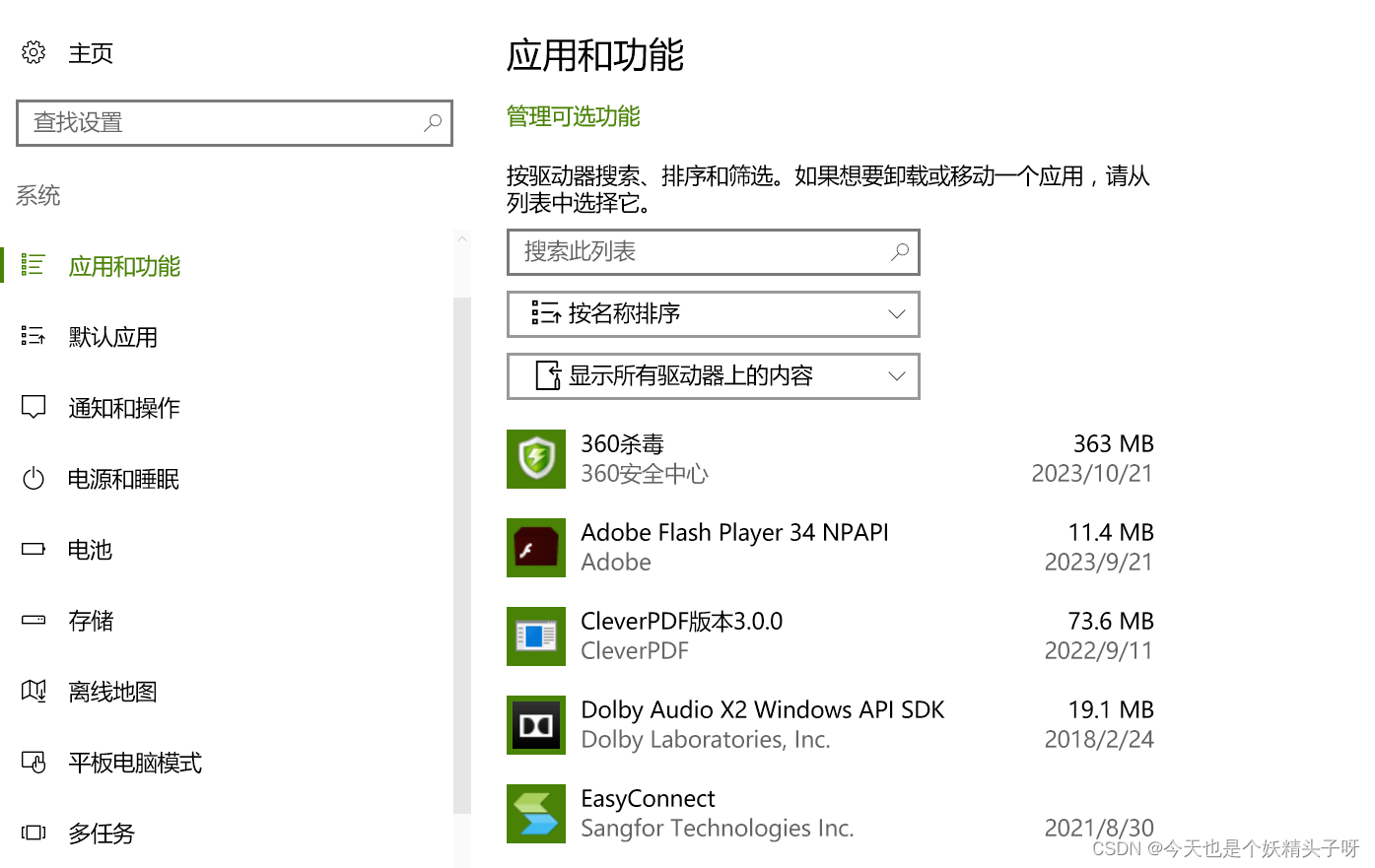
磁盘清理 | 已经卸载的软件还出现在应用和功能里怎么办?
一句话总结解决方法: 安装Geek Uninstaller,删除卸载残留。 问题描述: 最近磁盘满了,需要删除一些平时不常用的软件,但是发现一个问题。就是已经删除的软件,仍然会出现在“应用与功能”中。并且显示卸载图标为灰色&am…...
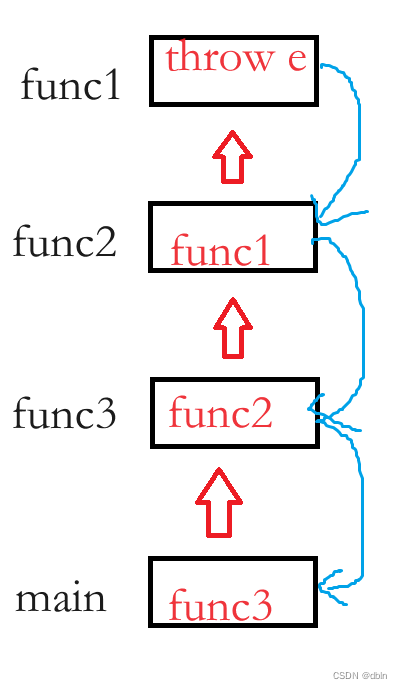
C++之异常
目录 一、C语言传统的处理错误的方式 二、C的异常 1、概念 2、关键字 3、基本格式 三、异常的抛出和捕获 1、异常的抛出和匹配原则 2、 在函数调用链中异常栈展开匹配原则 四、异常抛派生类,基类捕获 五、异常的重新抛出 六、异常安全 七、异常的优缺点…...
动态天气预报:Living Weather HD for Mac
Living Weather HD能够为Mac用户提供及时、准确、个性化的天气信息,并提供了丰富的定制选项,使用户能够更加方便地查看天气状况。 具有以下特点: 显示世界各地的准确天气预报和当地时间。自动探测出用户所在的首个地点,并通过搜…...

深度神经网络时与协方差矩阵
平时训练深度神经网络时,什么时候用到了协方差矩阵 在深度神经网络的平时训练过程中,一般情况下不直接使用协方差矩阵。然而,协方差矩阵的概念和相关性的考虑在某些情况下可以对网络的训练和优化起到一定的指导作用。 下面是一些与协方差矩…...
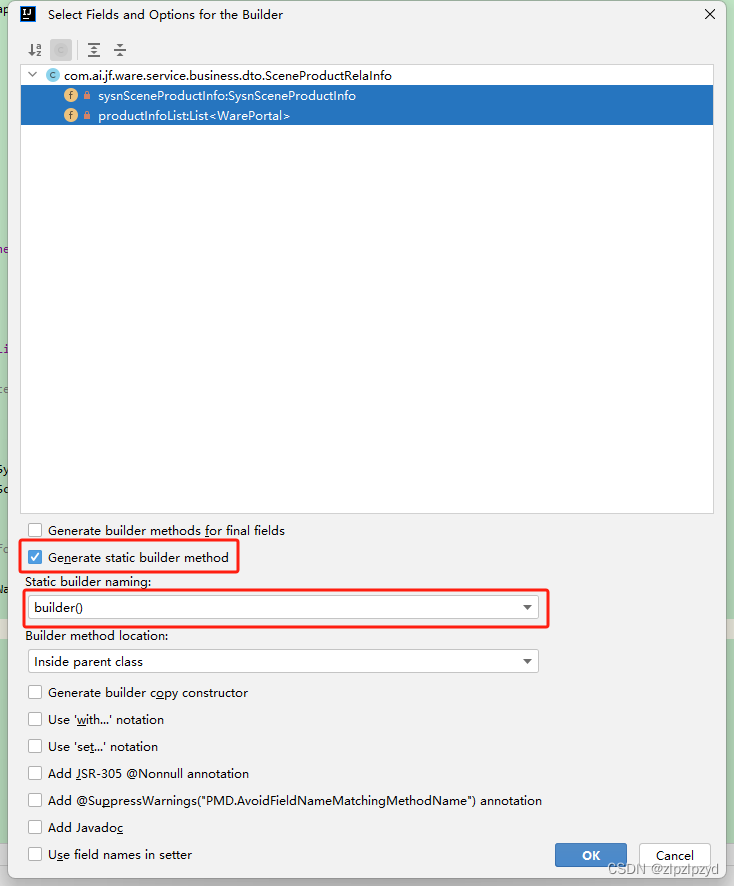
idea中java类属性(字段)链式赋值
很多人看到标题可能会想到 lombok 的 Builder,lombok 在国内用的挺多的,开源的组件中 mybatis-plus 中用到了这个,使用这个有一个问题就是通过对应 get 和 set 方法找不到对应的赋值方法,因为 lombok 使用了 apt 在编译期生成了相…...
)
vue通知(滚动)
1. li宽度不顾定 <template><div id"app"><div id"box" mouseover"clearLeft" mouseleave"setLeft"><ul :style"{ transform: translateX( left px) }" ref"cmdlist"><li v-for&qu…...

linux安装新版本git2、配置github-ssh。(centos、aws)
一、安装Git 1、yum默认版本git #1.安装git sudo yum install git -y #2.确认Git已经安装成功 git --version如果要安装较新版本,可以安装一个repo ,但是我这第一次尝试失败了,执行完提示找不到git2u,ius repo也连不上。而且每次…...

毅速丨3D打印结合拓扑优化 让轻量化制造更容易
制造轻量化对于提高能源利用效率、提高产品性能和减少环境影响,推动制造业的绿色化、高质量发展具有重要的促进作用。 轻量化设计对许多领域都有着重要影响,尤其是那些需要降低能源消耗、提高运输效率或减少对环境影响的领域。如航空航天,轻量…...
)
6252: 【C1】【分支】比较大小(一)
目录 题目描述 输入 输出 样例输入 样例输出 提示 来源 C代码: 题目描述 输入两个整数,输出较大数(两数相等输出任意一个) 输入 两行 第一行一个整数:m 第二行一个整数:n ( -30000 < m , n…...
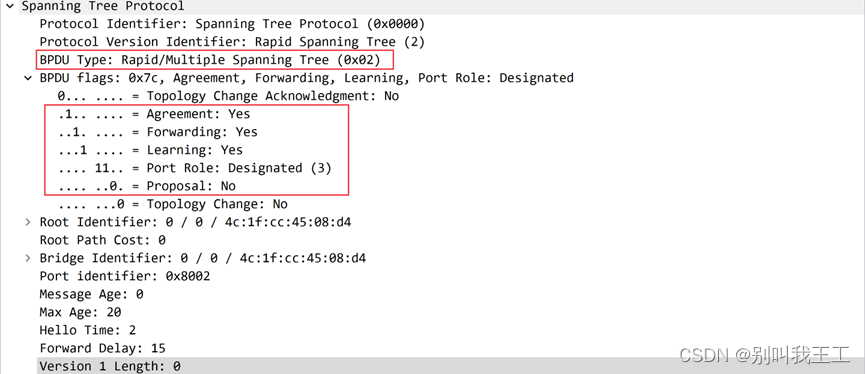
网工实验手册:RSTP如何配置?
1. 实验目的 熟悉RSTP的应用场景掌握RSTP的配置方法 想要华为数通配套实验拓扑和配置笔记的朋友们点赞关注,评论区留下邮箱发给你! 2. 实验拓扑 实验拓扑如图所示: 图:RSTP的配置 3. 实验步骤 (1) …...
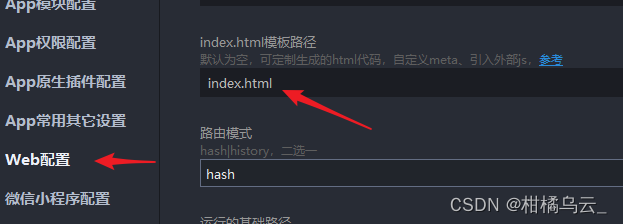
uniapp开发h5引入第三方js(sdk)
manifest.json 应用配置 | uni-app官网 根据文档上描述需要自定义模板的场景为: 方法一: 起初以为是在原有的index.html基础上再新建一个html文件,在项目根目录建立一个template.h5.html(仿照hello-uni-app项目)&…...

Could not find artifact com.sleepycat;je:jar:7.3.7 in aliyunmaven
在编译inlong源码时报的错误,去本地库里发现只有lastupdate的文件,就又去maven库里看了一下Maven Repository: com.sleepycat je (mvnrepository.com),发现没有这个版本,将版本进行修改错误解决...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
