LC-1402. 做菜顺序(记忆化搜索 ==> 动态规划、贪心)
1402. 做菜顺序
困难
一个厨师收集了他 n 道菜的满意程度 satisfaction ,这个厨师做出每道菜的时间都是 1 单位时间。
一道菜的 「 like-time 系数 」定义为烹饪这道菜结束的时间(包含之前每道菜所花费的时间)乘以这道菜的满意程度,也就是 time[i]*satisfaction[i] 。
返回厨师在准备了一定数量的菜肴后可以获得的最大 like-time 系数 总和。
你可以按 任意 顺序安排做菜的顺序,你也可以选择放弃做某些菜来获得更大的总和。
示例 1:
输入:satisfaction = [-1,-8,0,5,-9]
输出:14
解释:去掉第二道和最后一道菜,最大的 like-time 系数和为 (-1*1 + 0*2 + 5*3 = 14) 。每道菜都需要花费 1 单位时间完成。
示例 2:
输入:satisfaction = [4,3,2]
输出:20
解释:可以按照任意顺序做菜 (2*1 + 3*2 + 4*3 = 20)
示例 3:
输入:satisfaction = [-1,-4,-5]
输出:0
解释:大家都不喜欢这些菜,所以不做任何菜就可以获得最大的 like-time 系数。
提示:
n == satisfaction.length1 <= n <= 500-1000 <= satisfaction[i] <= 1000
记忆化搜索 ==> 动态规划
class Solution {int[] satisfaction;int[][] cache;public int maxSatisfaction(int[] satisfaction) {Arrays.sort(satisfaction);this.satisfaction = satisfaction;int n = satisfaction.length;cache = new int[n][n];for(int i = 0; i < n; i++)Arrays.fill(cache[i], -1);return dfs(0, 0);}// 定义dfs(i, cnt) 表示 枚举到i,0-i中选择了cnt个菜,可以获得的最大系数总和// 转移 每个菜肴可以选或者不选public int dfs(int i, int cnt){if(i == satisfaction.length){return 0;}if(cache[i][cnt] >= 0) return cache[i][cnt];int res = 0;res = Math.max(res, dfs(i+1, cnt+1) + (cnt+1) * satisfaction[i]);res = Math.max(res, dfs(i+1, cnt));return cache[i][cnt] = res;}
}
转动态规划
class Solution {public int maxSatisfaction(int[] satisfaction) {Arrays.sort(satisfaction);int n = satisfaction.length;int[][] f = new int[n+1][n+1];int res = 0;for(int i = 0; i < n; i++){for(int j = 0; j <= i; j++){// 选f[i+1][j+1] = f[i][j] + satisfaction[i] * (j+1);if(j+1 < i)// 不选f[i+1][j+1] = Math.max(f[i+1][j+1], f[i][j+1]);res = Math.max(res, f[i+1][j+1]);}}return res;}
}
贪心
https://leetcode.cn/problems/reducing-dishes/solutions/2492854/mei-ju-zuo-ji-dao-cai-tan-xin-pythonjava-k7w2/?envType=daily-question&envId=2023-10-22
class Solution {/**贪心1. a[i]大的菜要后做 1*4+2*3 < 1*3+/*42. 将nums从大到小排序令k表示做的菜f(k) = k*a[0] + (k-1)*a[1] + ... + 2*a[k-2] + a[k-1]每一项去掉一个a[i],得到 f(k-1)(k-1)*a[0] + (k-2)*a[1] + ... + a[k-2]即 f(k) = f(k-1) + (a[0] + a[1] + .. + a[k-1])右边的和式是 a 的前缀和,可以一遍遍历a,一边将a[i]累加到一个变量s中*/public int maxSatisfaction(int[] satisfaction) {Arrays.sort(satisfaction);int f = 0; // f(0) = 0int s = 0;for(int i = satisfaction.length-1; i >= 0; i--){s += satisfaction[i];if(s <= 0){ // 后面不可能找到更大的f(k)break;}f += s; // f(k) = f(k-1) + s}return f;}
}
相关文章:
)
LC-1402. 做菜顺序(记忆化搜索 ==> 动态规划、贪心)
1402. 做菜顺序 困难 一个厨师收集了他 n 道菜的满意程度 satisfaction ,这个厨师做出每道菜的时间都是 1 单位时间。 一道菜的 「 like-time 系数 」定义为烹饪这道菜结束的时间(包含之前每道菜所花费的时间)乘以这道菜的满意程度&#x…...

泰森多边形
泰森多边形 93 泰森多边形又叫沃洛诺伊图(Voronoi diagram),得名于Georgy Voronoi,是一组由连接两邻点线段的垂直平分线组成的连续多边形。一个泰森多边形内的任一点到构成该多边形的控制点的距离小于到其他多边形控制点的距离。…...

YOLOV8 进行docker环境配置
修改docker文件 原docekerfile中ADD https://ultralytics.com/assets/Arial.ttf https://ultralytics.com/assets/Arial.Unicode.ttf /root/.config/Ultralytics/下载很慢,可以在外部下载好,放入docker文件夹中,再将源代码改为ADD Arial.ttf…...
)
sealos一键部署K8S环境(sealos3.0时代教程过时了,目前已经4.0了,请移步使用Sealos一键安装K8S)
1 安装Sealos(4.0版本) sealos部署k8s贼方便,只需要一条init命令即可,3分钟部署完(下载安装包的时间不算)。 官方教程:https://www.sealyun.com/instructions/1st #主机名: hostnamectl set-hostname mas…...
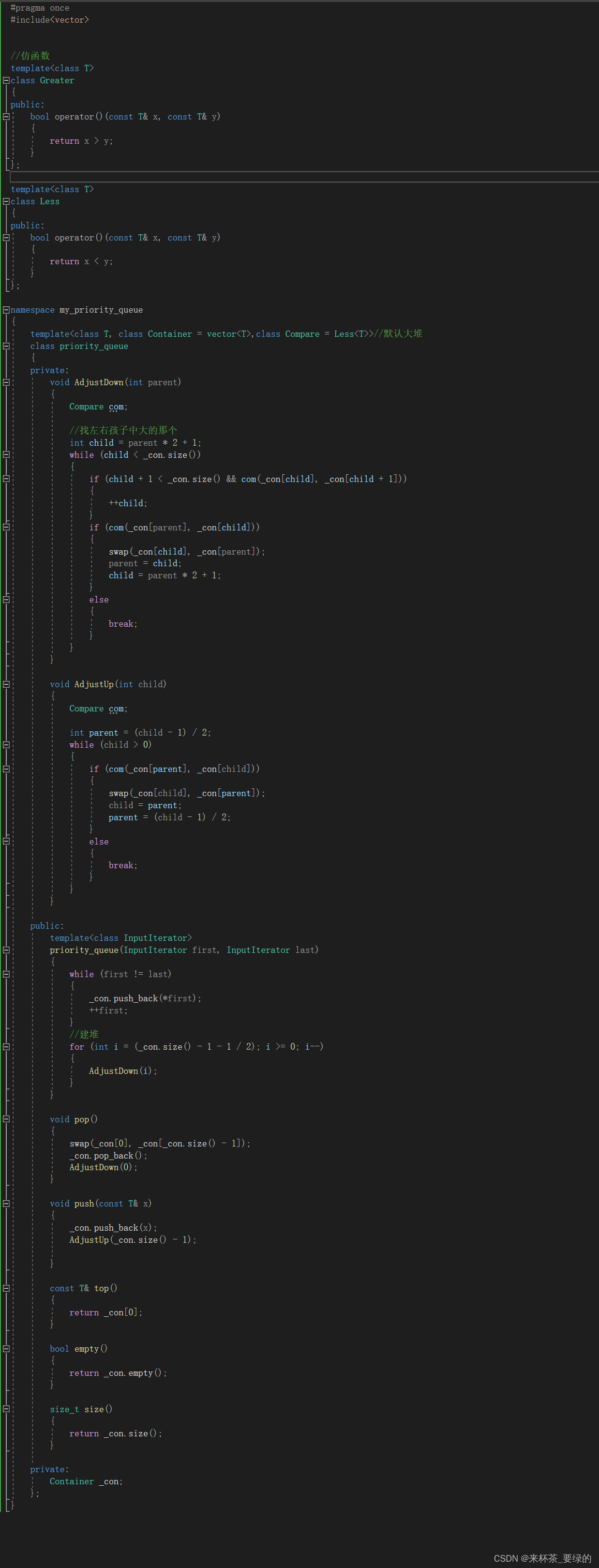
【C++】stackqueue
适配器是一种设计模式 , 该种模式是将一个类的接口转换成客户希望的另外一个接口 。 虽然 stack 和 queue 中也可以存放元素,但在 STL 中并没有将其划分在容器的行列,而是将其称为 容器适配 器 ,这是因为 stack 和队列只是对其他容…...

Hive篇面试题+详解
Hive篇面试题 1.什么是Hive?它的主要功能是什么? Hive是一个基于Hadoop的数据仓库工具,它提供了一个类SQL的查询语言(HiveQL)来查询和分析存储在Hadoop集群中的大规模数据。Hive的主要功能是将结构化数据映射到Hadoop…...

Mysql批量插入更新如何拆分大事务?
拆分大事务 一、解决方案二、遇到问题之前在运行Mysql任务的时候报错:binlog(1610646347 bytes) write threshold exceeded,原因是Mysql任务提交的是个大事务,超出binlog设定阈值,使得系统自动终止事务 一、解决方案 使用limit分页拆分大事务 CREATE PROCEDURE `split_tran…...
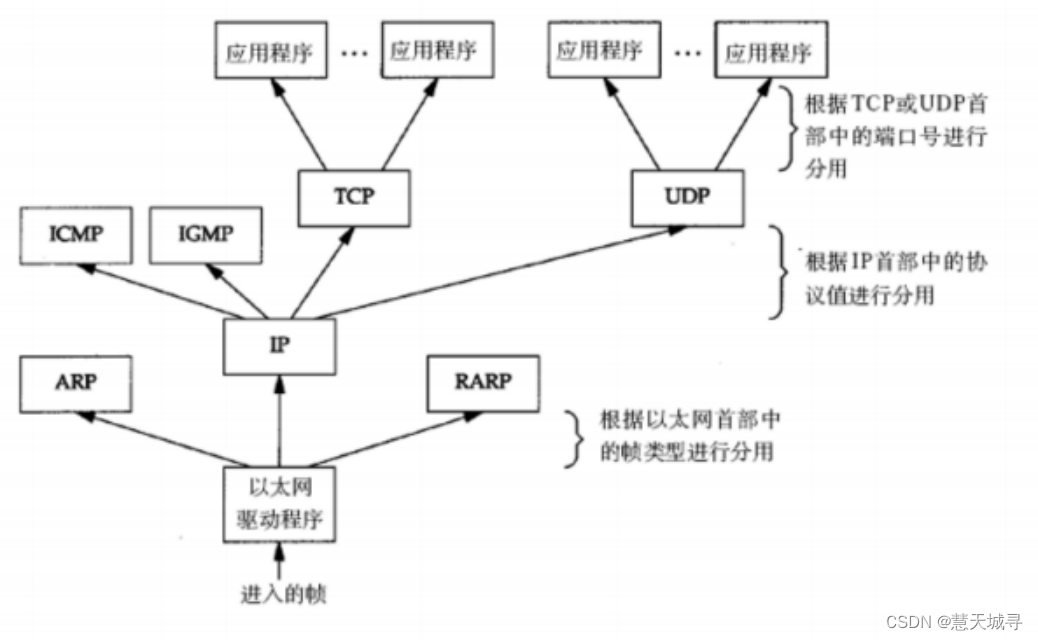
【计算机网络原理】初始网络基础
文章目录 1. 网络发展史1.1 单机时代1.2 网络互连局域网 LAN广域网 WAN 2. 网络通信基础2.1 IP 地址2.2 端口号2.3 协议2.4 五元组2.5 协议分层2.5.1 OSI七层模型2.5.2 TCP/IP五层模型 2.6 封装和分用2.6.1 数据封装(发送方情况)2.6.2 数据分用(接收方情况) 总结 1. 网络发展史…...
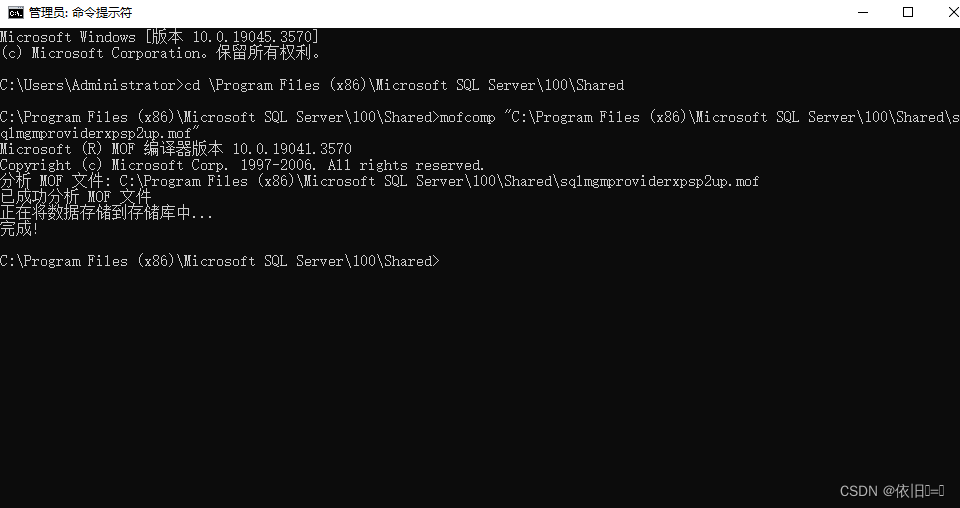
【sqlserver】配置管理器打不开
问题描述 无法连接到 WMI 提供程序。您没有权限或者该服务器无法访问。请注意,您只能使用SQL Server 配置管理器来管理 SQL Server 2005 和更高版本的服务 器。无效类[0x80041010] 解决方式: 命令提示符-右键-以管理员身份运行,再把以下代码执行一遍&…...
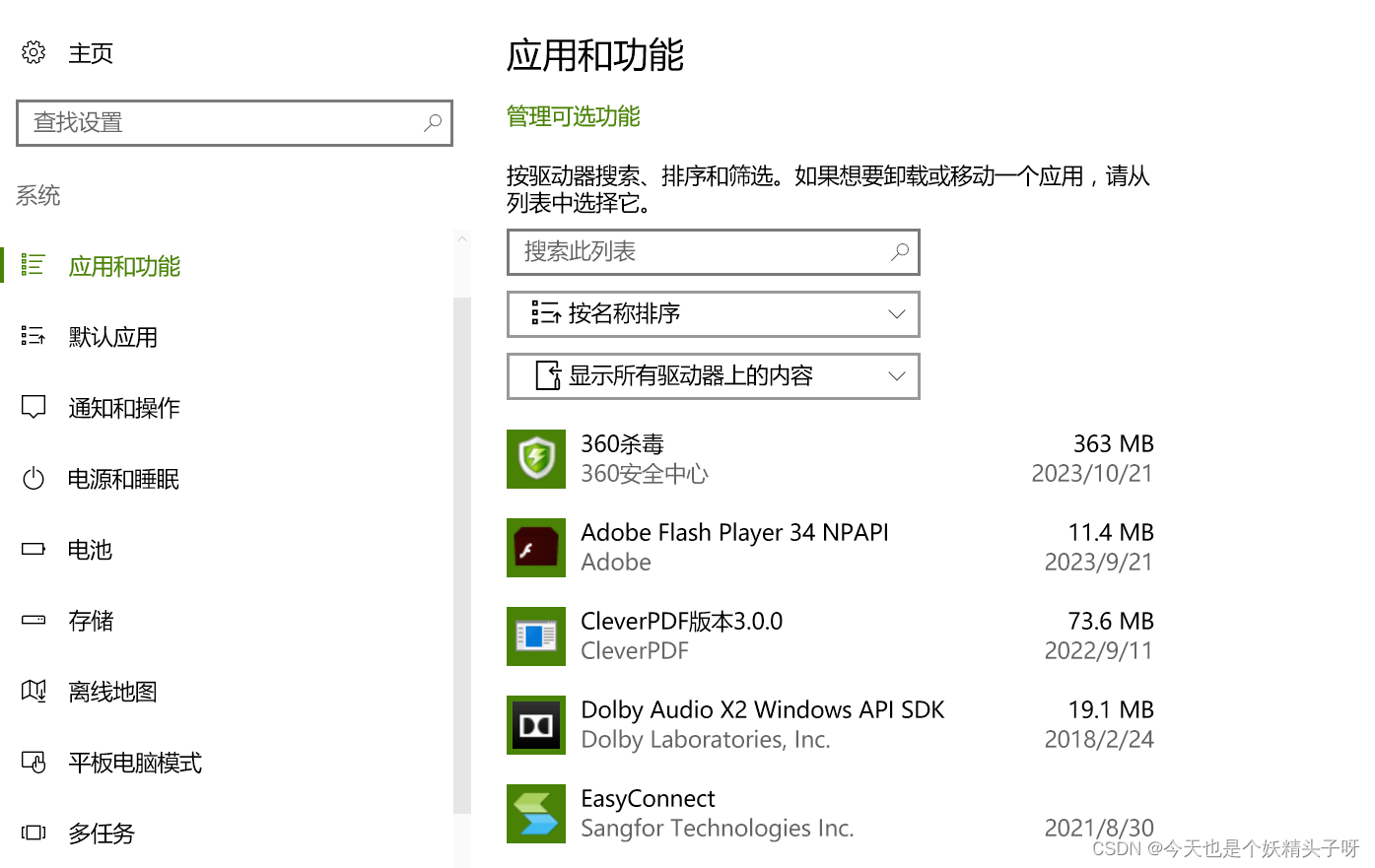
磁盘清理 | 已经卸载的软件还出现在应用和功能里怎么办?
一句话总结解决方法: 安装Geek Uninstaller,删除卸载残留。 问题描述: 最近磁盘满了,需要删除一些平时不常用的软件,但是发现一个问题。就是已经删除的软件,仍然会出现在“应用与功能”中。并且显示卸载图标为灰色&am…...
C++之异常
目录 一、C语言传统的处理错误的方式 二、C的异常 1、概念 2、关键字 3、基本格式 三、异常的抛出和捕获 1、异常的抛出和匹配原则 2、 在函数调用链中异常栈展开匹配原则 四、异常抛派生类,基类捕获 五、异常的重新抛出 六、异常安全 七、异常的优缺点…...
动态天气预报:Living Weather HD for Mac
Living Weather HD能够为Mac用户提供及时、准确、个性化的天气信息,并提供了丰富的定制选项,使用户能够更加方便地查看天气状况。 具有以下特点: 显示世界各地的准确天气预报和当地时间。自动探测出用户所在的首个地点,并通过搜…...

深度神经网络时与协方差矩阵
平时训练深度神经网络时,什么时候用到了协方差矩阵 在深度神经网络的平时训练过程中,一般情况下不直接使用协方差矩阵。然而,协方差矩阵的概念和相关性的考虑在某些情况下可以对网络的训练和优化起到一定的指导作用。 下面是一些与协方差矩…...
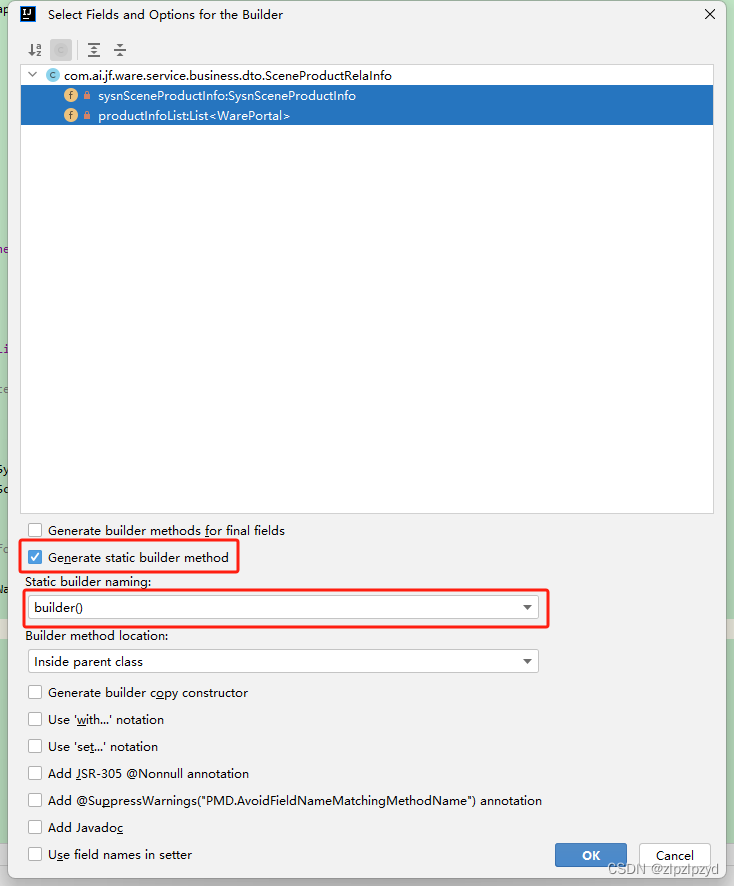
idea中java类属性(字段)链式赋值
很多人看到标题可能会想到 lombok 的 Builder,lombok 在国内用的挺多的,开源的组件中 mybatis-plus 中用到了这个,使用这个有一个问题就是通过对应 get 和 set 方法找不到对应的赋值方法,因为 lombok 使用了 apt 在编译期生成了相…...
)
vue通知(滚动)
1. li宽度不顾定 <template><div id"app"><div id"box" mouseover"clearLeft" mouseleave"setLeft"><ul :style"{ transform: translateX( left px) }" ref"cmdlist"><li v-for&qu…...

linux安装新版本git2、配置github-ssh。(centos、aws)
一、安装Git 1、yum默认版本git #1.安装git sudo yum install git -y #2.确认Git已经安装成功 git --version如果要安装较新版本,可以安装一个repo ,但是我这第一次尝试失败了,执行完提示找不到git2u,ius repo也连不上。而且每次…...

毅速丨3D打印结合拓扑优化 让轻量化制造更容易
制造轻量化对于提高能源利用效率、提高产品性能和减少环境影响,推动制造业的绿色化、高质量发展具有重要的促进作用。 轻量化设计对许多领域都有着重要影响,尤其是那些需要降低能源消耗、提高运输效率或减少对环境影响的领域。如航空航天,轻量…...
)
6252: 【C1】【分支】比较大小(一)
目录 题目描述 输入 输出 样例输入 样例输出 提示 来源 C代码: 题目描述 输入两个整数,输出较大数(两数相等输出任意一个) 输入 两行 第一行一个整数:m 第二行一个整数:n ( -30000 < m , n…...
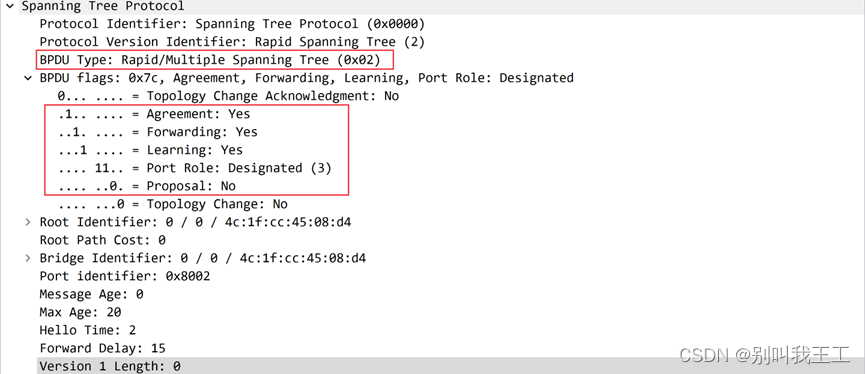
网工实验手册:RSTP如何配置?
1. 实验目的 熟悉RSTP的应用场景掌握RSTP的配置方法 想要华为数通配套实验拓扑和配置笔记的朋友们点赞关注,评论区留下邮箱发给你! 2. 实验拓扑 实验拓扑如图所示: 图:RSTP的配置 3. 实验步骤 (1) …...
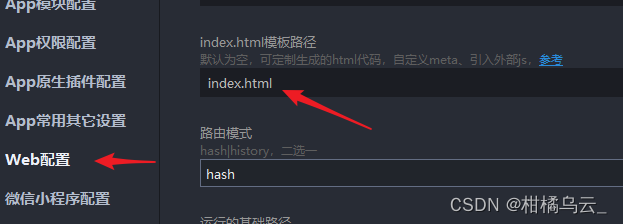
uniapp开发h5引入第三方js(sdk)
manifest.json 应用配置 | uni-app官网 根据文档上描述需要自定义模板的场景为: 方法一: 起初以为是在原有的index.html基础上再新建一个html文件,在项目根目录建立一个template.h5.html(仿照hello-uni-app项目)&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
