代码随想录打卡第四十六天|完全背包 ● 518. 零钱兑换 II ● 377. 组合总和 Ⅳ
完全背包理论
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
完全背包的物品是可以添加多次的,所以要从小到大去遍历
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
遍历物品和背包的循环是否可以颠倒?
在纯完全背包中,是可以的
循环顺序与排列组合的关系
外层for循环遍历物品,内层for遍历背包的情况 是组合数 不考虑元素顺序 因为后面的物品拿了就不能再取前面的了 所以无法生成排列数
外层for循环遍历背包,内层for遍历物品的情况 是排列数 考虑元素顺序 这个时候 前后物品顺序被打乱可以被随便排列
链接
518.零钱兑换II
**题目:**给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整数。
题目链接: 518.零钱兑换II
代码如下:
class Solution {public int change(int amount, int[] coins) {//可以凑成的方式//先背包再物品//dp[i]表示凑成i的方式if(amount==0){return 1;}if(amount==1){return 1;}int[] dp=new int[amount+1];dp[0]=1;for(int i=0;i<coins.length;i++){for(int j=coins[i];j<=amount;j++){dp[j]=dp[j]+dp[j-coins[i]];}}return dp[amount];}
}
377. 组合总和 Ⅳ
题目: 给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
题目链接: 377. 组合总和 Ⅳ
代码如下:
此题是排列 所以背包在外 物品在内
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.length; j++) {if (i >= nums[j]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
}
相关文章:

代码随想录打卡第四十六天|完全背包 ● 518. 零钱兑换 II ● 377. 组合总和 Ⅳ
完全背包理论 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。 完全背包和01背包问题唯一…...
【BP-Adaboost预测】基于BP神经网络的Adaboost的单维时间序列预测研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
Origami Studio for Mac:塑造未来,掌握原型设计之巅
在当今高度竞争的设计领域,原型设计的重要性不言而喻。它不仅是沟通想法,也是测试和改进设计的关键环节。而现在,一款强大的原型设计工具——Origami Studio for Mac,正在席卷设计界,以其独特的功能和卓越的性能&#…...
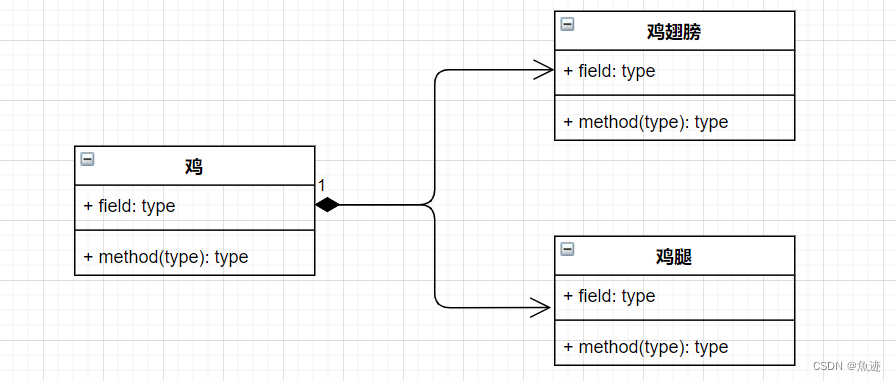
UML类图中各箭头表示总结
UML类图中各箭头表示总结 1、泛化2、实现3、依赖4、关联5、聚合6、组合 在UML类图中,箭头关系是用来表示类之间的关系的。箭头关系的种类有以下几种: 1、泛化 泛化:表示类之间的继承关系。箭头从子类指向父类。箭头:实线空心三角…...
神经网络量化----为了部署而特别设计
引言:一般神经网络量化有两个目的: 为了加速,在某些平台上浮点数计算比较耗费时间,替换为整形可以加快运算为了部署,某些平台上只支持整形运算,比如在芯片中如果是第1个目的,则使用常规的量化手段就可以满足,将浮点数运算变成整形运算+较少的浮点运算 但是如果是第2个目…...

代码随想录算法训练营Day60|单调栈01
代码随想录算法训练营Day60|单调栈01 文章目录 代码随想录算法训练营Day60|单调栈01一、739. 每日温度二、496.下一个更大元素 I 一、739. 每日温度 class Solution {public int[] dailyTemperatures(int[] temperatures) {//单调栈int lenstemperatures.length;int result[]n…...

openMP学习笔记 -编程模型
OpenMP模型 gcc编译openmp指令:gcc test.cpp -o test -fopenmp 定积分计算 函数面积 给定一个定积分,计算其面积: ∫ 0 1 4.0 ( 1 x 2 ) d x \int^{1}_{0}{\frac{4.0}{(1x^2)}dx} ∫01(1x2)4.0dx omp 概念 并行区域 并行区域用于…...

【Hive SQL 每日一题】环比增长率、环比增长率、复合增长率
文章目录 环比增长率同比增长率复合增长率测试数据需求说明需求实现 环比增长率 环比增长率是指两个相邻时段之间某种指标的增长率。通常来说,环比增长率是比较两个连续时间段内某项数据的增长量大小的百分比。 环比增长率反映了两个相邻时间段内某种经济指标的变…...
)
Java设计模式之外观模式(Facade Pattern)
外观模式(Facade Pattern)是一种结构型设计模式,它提供了一个统一的接口,用于访问子系统中的一组接口。外观模式通过隐藏子系统的复杂性,简化了客户端与子系统之间的交互,提供了一个更简单、更直观的接口。…...

【大疆智图】大疆智图(DJI Terra 3.0.0)安装及使用教程
大疆智图是一款以二维正射影像与三维模型重建为主的软件,同时提供二维多光谱重建、激光雷达点云处理、精细化巡检等功能。它能够将无人机采集的数据可视化,实时生成高精度、高质量三维模型,满足事故现场、工程监测、电力巡线等场景的展示与精确测量需求。 文章目录 1. 安装D…...
腾讯地图基本使用(撒点位,点位点击,弹框等...功能) 搭配Vue3
腾讯地图的基础注册账号 展示地图等基础功能在专栏的上一篇内容 大家有兴趣可以去看一看 今天说的是腾讯地图的在稍微一点的基础操作 话不多说 直接上代码 var marker ref(null) var map var center ref(null) // 地图初始化 const initMap () > {//定义地图中心点坐标…...
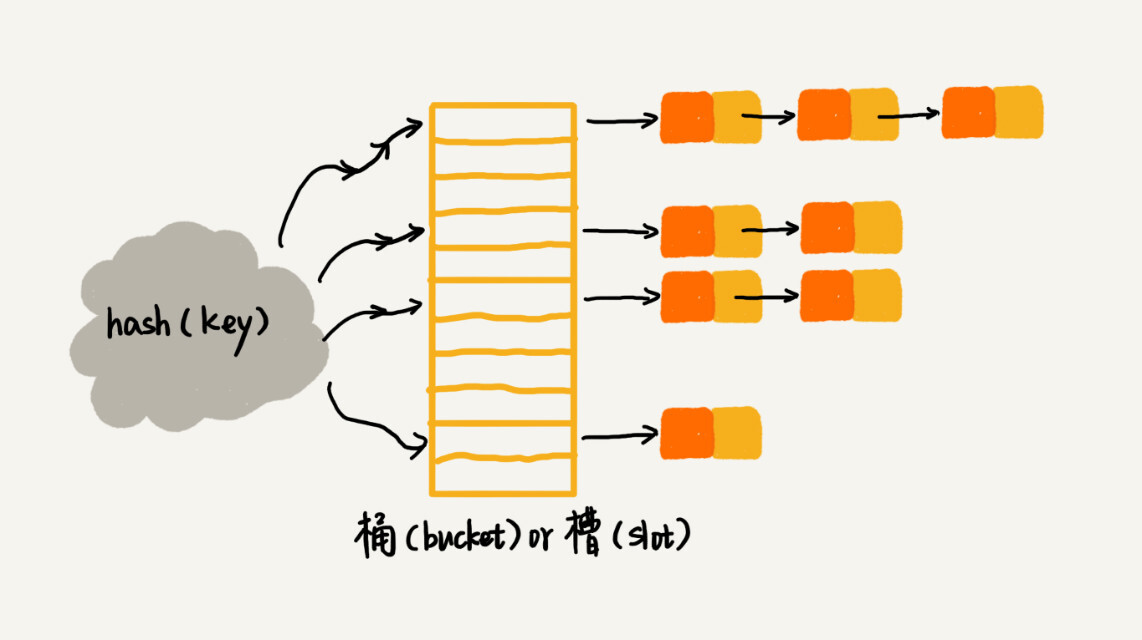
散列表:Word文档中的单词拼写检查功能是如何实现的?
文章来源于极客时间前google工程师−王争专栏。 一旦我们在Word里输入一个错误的英文单词,它就会用标红的方式提示“编写错误”。Word的这个单词拼写检查功能,虽然很小但却非常实用。这个功能是如何实现的? 散列别(Hash Table&am…...

智慧公厕蜕变多功能城市智慧驿站公厕的创新
随着城市发展的不断推进,对公共设施的便利性和智能化要求也日益提高。为满足市民对高品质、便捷、舒适的公共厕所的需求,智慧公厕行业的领航厂家广州中期科技有限公司,全新推出了一体化智慧公厕驿站。凭借着“高科技碳中和物联网创意设计新经…...

R语言清洗与处理数据常用代码段
去掉数据框df的某一列: # 删除不必要的变量 data$unnecessary_var <- NULL 选择需要的列进行读入数据框: # 选择需要的列 selected_cols <- c("col1", "col2", "col3") data <- fread("data.csv", s…...

centos 7.9 安装python 3.10的tls问题,
本地开发升级成了py3.10.6,服务器测试时安装py3.10.4 发现无法正常使用pip3 pip is configured with locations that require TLS/SSL, however the ssl module in Python is not available. 印象中py3的高版本依赖高版本的openssl,centos 7下默认的openssl为1.0.x, 问题很简…...

pytorch,tf维度理解RNN
input_t input_t.squeeze(1) 这行代码用于从 input_t 中去除尺寸为1的维度。在深度学习中,经常会出现具有额外尺寸为1的维度,这些维度通常是为了匹配模型的期望输入维度而添加的。 在这里,input_t可能具有形状 (batch_size, 1, feature_dim…...

算法刷题-数组
算法刷题 209. 长度最小的子数组-二分或者滑动窗口 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数…...
可视化数学分析软件 MATLAB R2021b mac中文版软件介绍
MATLAB R2021b mac作为数学类科技应用软件中首屈一指的商业数学软件,可以帮助您进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。…...

罗技摄像头左右翻转
需要下载驱动lws(我的是c310) LWS 罗技摄像头驱动下载 打开驱动程序,高级设置。有个镜像。...
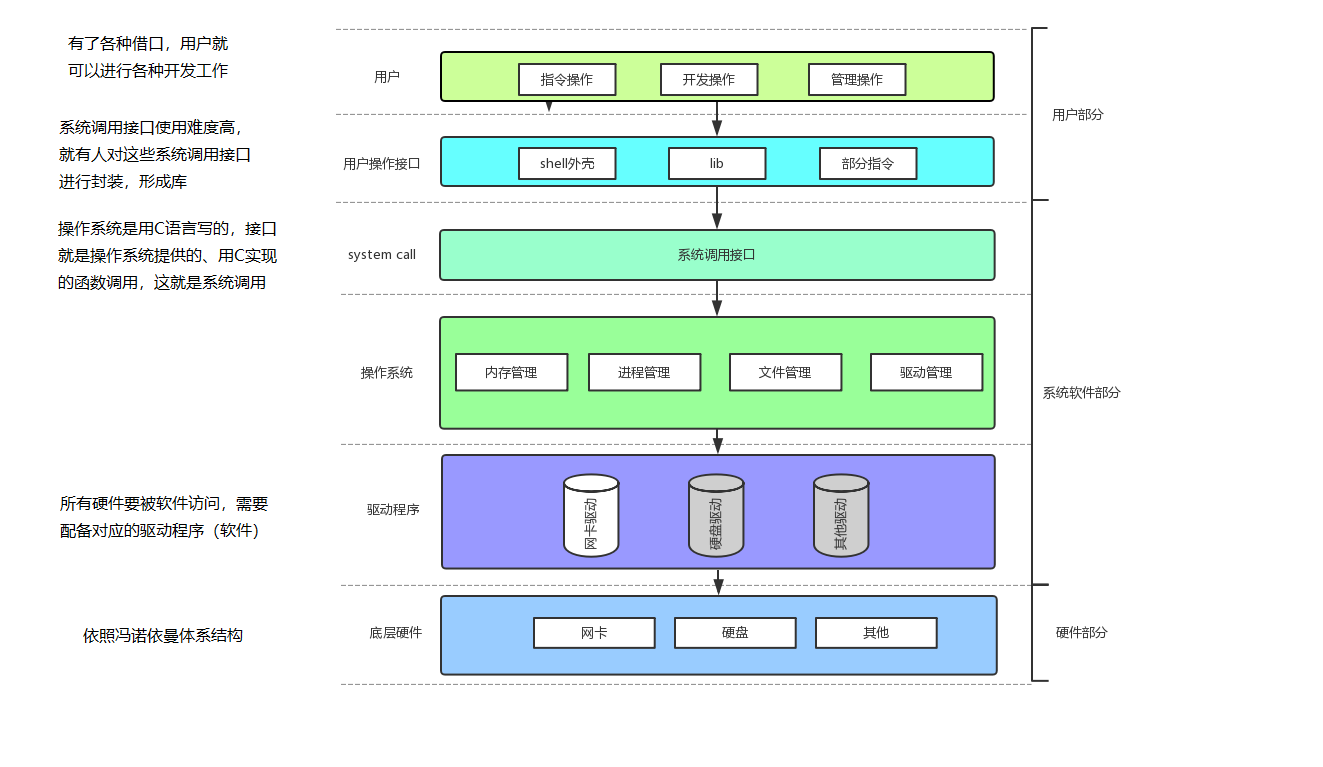
【Linux】操作系统的认识
操作系统 1. 冯诺依曼体系结构2. 操作系统 1. 冯诺依曼体系结构 冯诺依曼体系结构的介绍 冯.诺依曼结构消除了原始计算机体系中,只能依靠硬件控制程序的状况(程序作为控制器的一部分,作为硬件存在),将程序编码存储在…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
