代码随想录Day24 LeetCode T491 递增子序列 LeetCode T46 全排列 LrrtCode T47 全排列II
LeetCode T491 递增子序列

题目链接:491. 递增子序列 - 力扣(LeetCode)
题目思路:
首先这里的测试用例很容易误导我们,这道题不能使用上次子集的思路对数组先排序,使用一个used数组来解决问题.
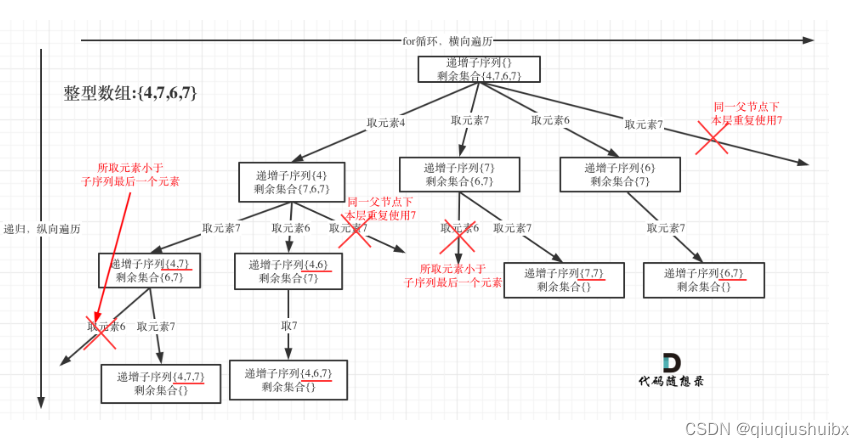
我们用[4,7,6,7]举例这道题的递增序列不存在[4,6,7,7]这个子序列,而如果我们对数组先进行排序,就会得到错误答案.
这题的实质是让我们在数组中递增的取出元素,实际上是我们取出的元素是有序的,这里我们可以定义一个set来解决问题,实际上我们要做的仍然是树层去重,这里只要对每一层的元素进行一次去重即可
1.函数定义
其他的都定义为全局变量了,只需这两个参数即可
public void backtracking(int[] nums,int startIndex)2.终止条件
这题跟之前一样,不需要终止条件,因为我们收集的是树的所有节点,而不是叶子结点,但是题目要求我们的path至少要大于等于2,所以我们就以这个为条件来收集结果.
if(path.size()>=2){result.add(new ArrayList(path));}3.一次搜索逻辑(for循环)
注:为什么set不需要回溯?
因为set是每一层都会重置的,无需回溯,每一层回溯会自动置空
Set<Integer> set = new HashSet<>();//每一层用来记录,去重for(int i = startIndex;i<nums.length;i++){if( !path.isEmpty() && path.get(path.size()-1) > nums[i] || set.contains(nums[i])){continue;}set.add(nums[i]);path.add(nums[i]);backtracking(nums,i+1);path.remove(path.size()-1);}
题目代码:
class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backtracking(nums,0);return result;}public void backtracking(int[] nums,int startIndex){if(path.size()>=2){result.add(new ArrayList(path));}Set<Integer> set = new HashSet<>();for(int i = startIndex;i<nums.length;i++){if( !path.isEmpty() && path.get(path.size()-1) > nums[i] || set.contains(nums[i])){continue;}set.add(nums[i]);path.add(nums[i]);backtracking(nums,i+1);path.remove(path.size()-1);}}
}LeetCode T46 全排列

题目链接:46. 全排列 - 力扣(LeetCode)
题目思路:
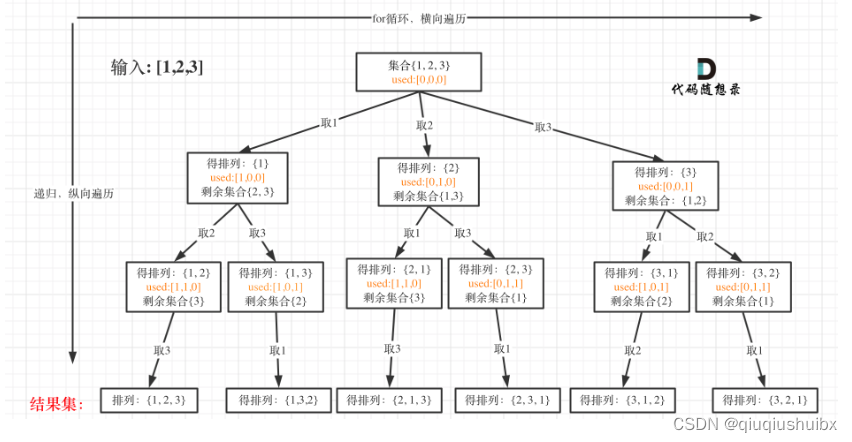
首先这题我们可以先画出树状图,这题的重点就是used数组的使用
因为排列是有序的,所以[1,2]和[2,1]是两个完全不同的排列,这里可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex,但是需要使用used数组,因为一个排列中nums数组中的每个元素都只能出现一次,这里我们就需要标记已经出现的元素,如果它还想出现,就可以直接continues这次循环即可,下面我们进行回溯三部曲
1.回溯函数参数
这里不需要根据startIndex来判断取值区间,也是和子集不同的地方,这里我们直接传入nums数组即可
public void backtracking(int[] nums)2.确定终止条件
这里是在叶子结点取值而不是取每个节点的值,所以需要终止条件,因为我们需要获得的是数组的排列,所以当path收集的元素长度到达数组的长度,即是一次有效的排列
if(path.size() == nums.length){result.add(new ArrayList(path));return;}3.一次搜索逻辑
这里我们首先不能再一次排列中重复出现某元素,所以在添加元素之前先判断该元素是否出现过,出现过那么该次全排列无效,则跳出本轮循环,下面就是经典的递归和回溯过程
for(int i = 0;i<nums.length;i++){if(used[i]){continue;}path.add(nums[i]);used[i] = true;backtracking(nums);path.remove(path.size()-1);used[i] = false;}
题目代码:
class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> result = new ArrayList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {used = new boolean[nums.length];backtracking(nums);return result;}public void backtracking(int[] nums){if(path.size() == nums.length){result.add(new ArrayList(path));return;}for(int i = 0;i<nums.length;i++){if(used[i]){continue;}path.add(nums[i]);used[i] = true;backtracking(nums);path.remove(path.size()-1);used[i] = false;}}
}LeetCode T47 全排列II

题目链接:47. 全排列 II - 力扣(LeetCode)
题目思路:
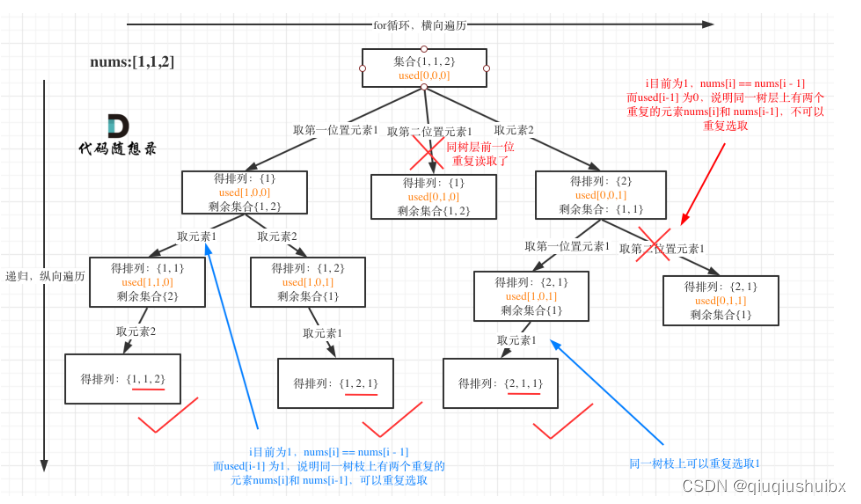
这题的思路和上一题类似,由于本题可能存在重复元素,所以比上一题多了一个去重的逻辑,这题的去重逻辑和之前组合的逻辑是一样的,我们只需要先将数组排序,让相同的元素排在一起,使用一个used数组来标记已经使用过的元素,这里我们还是先画出树状图来帮助理解
我们发现相邻元素如果是相等的,那么相同元素中的第二个元素开始的路径就重复了,也就是我们说的树层去重,下面我摆出树层去重的逻辑
if(i>0 && nums[i] == nums[i-1] && !used[i-1])其余代码和上面一样,我们依然按照回溯三部曲来操作
1.函数参数
由于其他元素都定义为全局变量了,所以直接使用一个nums即可,本题不需要startIndex来帮助我们规定选择元素的区间
public void backtracking(int[] nums)2.终止条件
这题终止条件仍然是path收集的长度到达nums的长度即可
if(path.size() == nums.length){result.add(new ArrayList(path));}3.一次搜索逻辑
这里就涉及我们的去重逻辑了,下面由于没有startIndex约束,所以我们对选取的元素增加一个条件,就是选取的元素必须没有被使用过
for(int i = 0;i<nums.length;i++){if(i>0 && nums[i] == nums[i-1] && !used[i-1]){continue;}if (!used[i]) {used[i] = true;//标记同⼀树⽀nums[i]使⽤过,防止同一树枝重复使用path.add(nums[i]);backtracking(nums);path.remove(path.size() - 1);//回溯,说明同⼀树层nums[i]使⽤过,防止下一树层重复used[i] = false;//回溯}}
题目代码:
class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> result = new ArrayList<>();boolean used[];public List<List<Integer>> permuteUnique(int[] nums) {used = new boolean[nums.length];Arrays.sort(nums);backtracking(nums);return result;}public void backtracking(int[] nums){if(path.size() == nums.length){result.add(new ArrayList(path));}for(int i = 0;i<nums.length;i++){if(i>0 && nums[i] == nums[i-1] && !used[i-1]){continue;}if (!used[i]) {used[i] = true;//标记同⼀树⽀nums[i]使⽤过,防止同一树枝重复使用path.add(nums[i]);backtracking(nums);path.remove(path.size() - 1);//回溯,说明同⼀树层nums[i]使⽤过,防止下一树层重复used[i] = false;//回溯}}}
}相关文章:
代码随想录Day24 LeetCode T491 递增子序列 LeetCode T46 全排列 LrrtCode T47 全排列II
LeetCode T491 递增子序列 题目链接:491. 递增子序列 - 力扣(LeetCode) 题目思路: 首先这里的测试用例很容易误导我们,这道题不能使用上次子集的思路对数组先排序,使用一个used数组来解决问题. 我们用[4,7,6,7]举例这道题的递增序列不存在[4,6,7,7]这个…...
【六:(mock数据)spring boot+mybatis+yml】
目录 1.1、代码编写Demo类User类启动类 APplication 1.2、配置类查询语句的配置 mysql.ymlspringboot的配置 application.yml日志的配置 logback.xml数据库的配置 mybatis-config.xml 1.3、测试:1.3.1、测试获取用户数1.3.2、添加用户1.3.3、数据的更新1.3.4、数据的…...

51单片机KeyWard
eg1: 单片机键盘的分类 键盘分为编码键盘和非编码键盘,键盘上闭合键的识别由专用的硬件编码器实现,并产生键编码号或键值得称为编码键盘,如计算机键盘,而靠软件来识别的称为非编码键盘,在单片机组成的各种…...

【简记】getprop, setprop 命令使用
getprop, setprop 命令使用 1、终端设置、读取系统属性 // 例 adb shell setprop "test" "1" adb shell getprop "test"2、安卓读取系统配置 部分属性需要通过反射 android.os.SystemProperties 的方法获取,参见 android 获取手机…...

Ubuntu22.04安装nvidia-docker
安装docker 参考这篇文章:Ubuntu22.04安装docker - 掘金 安装nvidia-docker 参考这篇文章:Ubuntu 22.04 LTS : NVIDIA Container Toolkit : Install : Server World 流程: curl -s -L https://nvidia.github.io/nvidia-docker/gpgkey | …...
)
简单的代码优化(后端)
上一篇谈了谈简单的前端的优化,这次就以下几点谈谈后端的优化。 书写时常见的。 循环里面不要走IO流。 走IO,是要对硬盘进读写操作的。就结论而言,硬盘的读写速度是低于内存的,比如说硬盘上读一次数据,需要1秒&#…...

3.Node-事件循环的用法
题记 node.js事件循环的使用方法 Node.js 是单进程单线程应用程序,但是因为 V8 引擎提供的异步执行回调接口,通过这些接口可以处理大量的并发,所以性能非常高。 Node.js 几乎每一个 API 都是支持回调函数的。 Node.js 基本上所有的事件机制都…...
2525.根据规则将箱子分类/并查集/动态规划
2525. 根据规则将箱子分类 - 力扣(LeetCode) 给你四个整数 length ,width ,height 和 mass ,分别表示一个箱子的三个维度和质量,请你返回一个表示箱子 类别 的字符串。 如果满足以下条件,那么…...
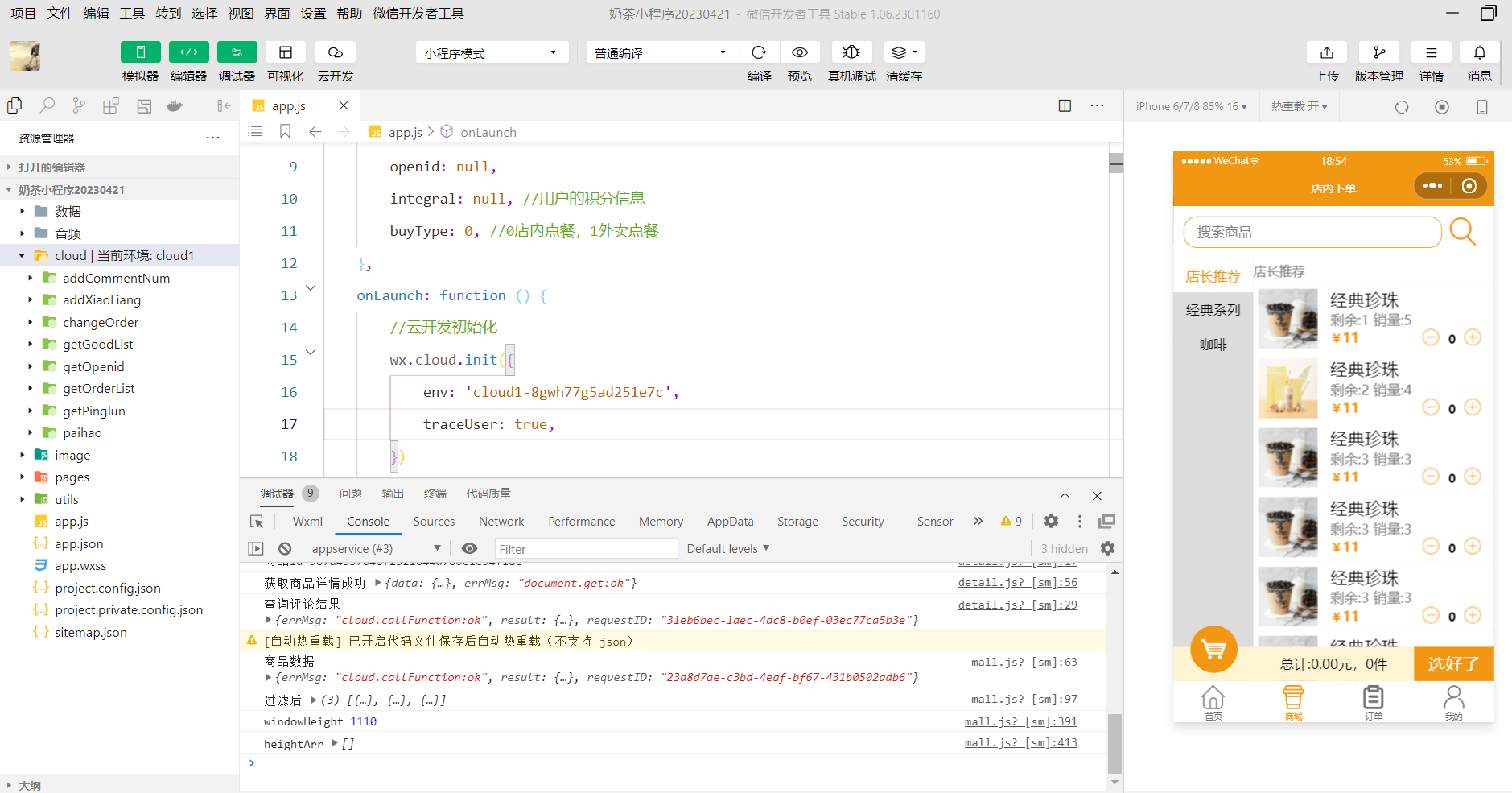
2023年10月小程序云开发cms内容管理无法使用,无法同步内容模型到云开发数据库的解决方案
一,问题描述 最近越来越多的同学找石头哥,说cms用不了,其实是小程序官方最近又搞大动作了,偷偷的升级的云开发cms(内容管理)以下都称cms,不升级不要紧,这一升级,就导致我…...

无论有没有按钮,iPhone都可以进行截屏操作!如何在iPhone上截屏
通过简单的按键组合,可以很容易地将iPhone屏幕的图片捕获到图像文件中,并保存到照片库中。以下是操作方法。 什么是屏幕截图 屏幕截图是指通常包含你在设备屏幕上看到的内容的精确副本的图像。在设备内拍摄的数字屏幕截图通常使用相机拍摄物理屏幕的照…...

笔记本平台信号讲解
1、power button:这个信号会引起SMI#或者SCI来表示系统请求进入到睡眠状态。如果系统已经处于睡眠状态,这将导致唤醒事件信号。 如果PWRBTN#键超过4秒,这将导致一个无条件的过渡(电源按钮替代)到S5状态。即使系统是在S1-S4的状态,覆盖也会发生。 这个信号有一个内部上拉…...
什么是Sectigo证书?
Sectigo证书,早前被称为Comodo证书,是一种SSL(安全套接层)证书,用于保护互联网上的数据传输的安全性和隐私性。这些证书由全球领先的SSL证书颁发机构Sectigo颁发,被广泛用于网站、应用程序和服务器上。本文…...

虹科 | 测试方案 | 汽车示波器 通讯网络(LIN/CAN/FlexRay)测试方案
通讯网络(LIN/CAN/FlexRay)测试 虹科CAN总线示波器把你的PC电脑变成一台功能强大的汽车测试工具,用于检测车辆网络各类通讯信号,如CAN Bus、CAN FD、LIN、FlexRay,还可以检测车上所有传感器和执行器的信号 串行译码 …...

ubuntu20.04安装MySQL8、MySQL服务管理、mysql8卸载
ubuntu20.04安装MySQL8 #更新源 sudo apt-get update #安装 sudo apt-get install mysql-serverMySQL服务管理 # 查看服务状态 sudo service mysql status # 启动服务 sudo service mysql start # 停止服务 sudo service mysql stop # 重启服务 sudo service mysql restart登…...

曾仕强老师视频+音频+电子书合集百度网盘资源
需要的扫码添加获取:...
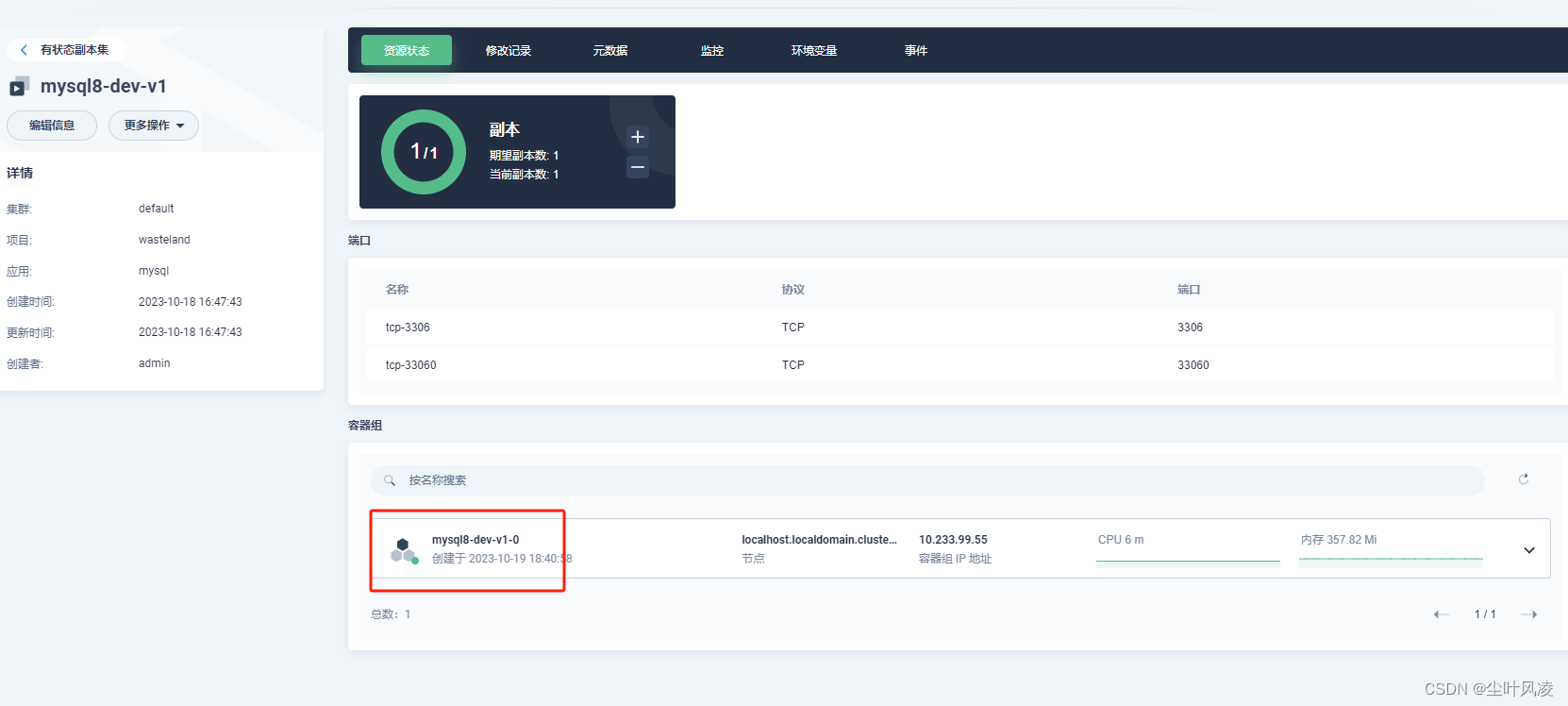
KubeSphere安装mysql8
需要持久化储存数据的,建立有状态服务。 无状态服务是不会持久化的,重启就归零 KubeSphere 创建自建应用后,创建有状态服务,但是自己应用的有状态服务不能外放端口,需要在服务哪里删除pod,在创建负载指定相…...

相似度loss汇总,pytorch code
用于约束图像生成,作为loss。 可梯度优化 pytorch structural similarity (SSIM) loss https://github.com/Po-Hsun-Su/pytorch-ssimhttps://github.com/harveyslash/Facial-Similarity-with-Siamese-Networks-in-Pytorch/blob/master/Siamese-networks-medium.ip…...
python中的yolov5结合PyQt5,使用QT designer设计界面没正确启动的解决方法
python中的yolov5结合PyQt5,使用QT designer设计界面没正确启动的解决方法 一、窗体设计test: 默认你已经设计好了窗体后: 这时你需要的是保存生成的untitle.ui到某个文件夹下,然后在命令行中奖.ui转换为.py(,通过…...

Milk-V Duo移植rt-thread smart
前言 (1)PLCT实验室实习生长期招聘:招聘信息链接 (2)首先,我们拿到Milk-V Duo板子之后,我个人建议先移植大核Linux。因为那个资料相对多一点,也简单很多,现象也容易观察到…...

会声会影2024有哪些新功能?好不好用
比如会声会影视频编辑软件,既加入光影、动态特效的滤镜效果,也提供了与色彩调整相关的LUT配置文件滤镜,可选择性大,运用起来更显灵活。会声会影在用户的陪伴下走过20余载,经过上百个版本的优化迭代,已将操作…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...