力扣每日一题48:旋转图像
题目描述:
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
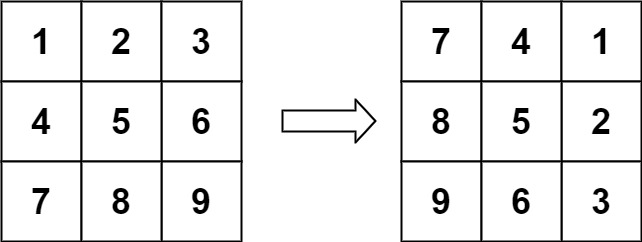
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
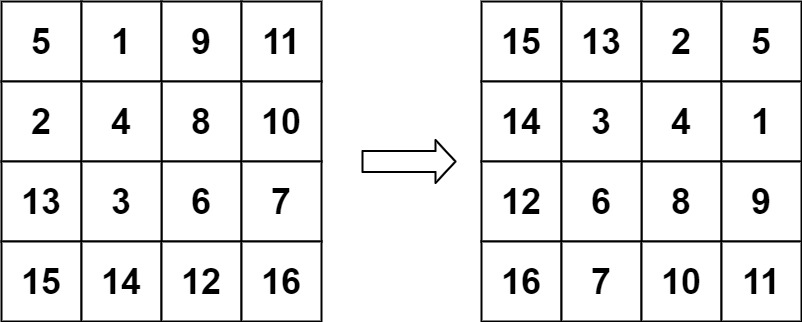
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
通过次数
495.6K
提交次数
659.8K
通过率
75.1%
题解和思路:
方法一:外层旋转然后向内层收缩。
做一个循环,每次循环时旋转矩阵最外层回字型,然后矩阵向内收缩,直到收缩到一个2*2矩阵或一个1*1矩阵时就停止。
代码:
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n=matrix.size();int lo=0,hi=n-1;while(lo<hi){vector<int> temp(hi-lo,0);//先换四个角,再换其它的int t=matrix[lo][lo];matrix[lo][lo]=matrix[hi][lo];matrix[hi][lo]=matrix[hi][hi];matrix[hi][hi]=matrix[lo][hi];matrix[lo][hi]=t;///去角后的四条边for(int i=0;i<hi-lo-1;i++) temp[i]=matrix[lo][lo+1+i];for(int i=0;i<hi-lo-1;i++) matrix[lo][hi-1-i]=matrix[lo+1+i][lo];//左边-》上面for(int i=0;i<hi-lo-1;i++) matrix[lo+1+i][lo]=matrix[hi][lo+1+i];//下面-->左边for(int i=0;i<hi-lo-1;i++) matrix[hi][lo+1+i]=matrix[hi-1-i][hi];//右边-->下面for(int i=0;i<hi-lo-1;i++) matrix[lo+1+i][hi]=temp[i];//上面-->右边lo++;hi--;}}
};方法二:反转代替旋转
先将矩阵通过水平轴翻转(即第一行和最后一行换,第二行和倒数第二行换......),再通过主对角线翻转,最后得到的矩阵和将原数组顺时针旋转90°的矩阵是一样的。不信的话可以自己拿一个长方形的纸片试一试。官方题解有这种思路,我直接放官方题解代码吧。
代码:
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();// 水平翻转for (int i = 0; i < n / 2; ++i) {for (int j = 0; j < n; ++j) {swap(matrix[i][j], matrix[n - i - 1][j]);}}// 主对角线翻转for (int i = 0; i < n; ++i) {for (int j = 0; j < i; ++j) {swap(matrix[i][j], matrix[j][i]);}}}
};相关文章:

力扣每日一题48:旋转图像
题目描述: 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 1: 输入:matrix [[1,2,3],…...
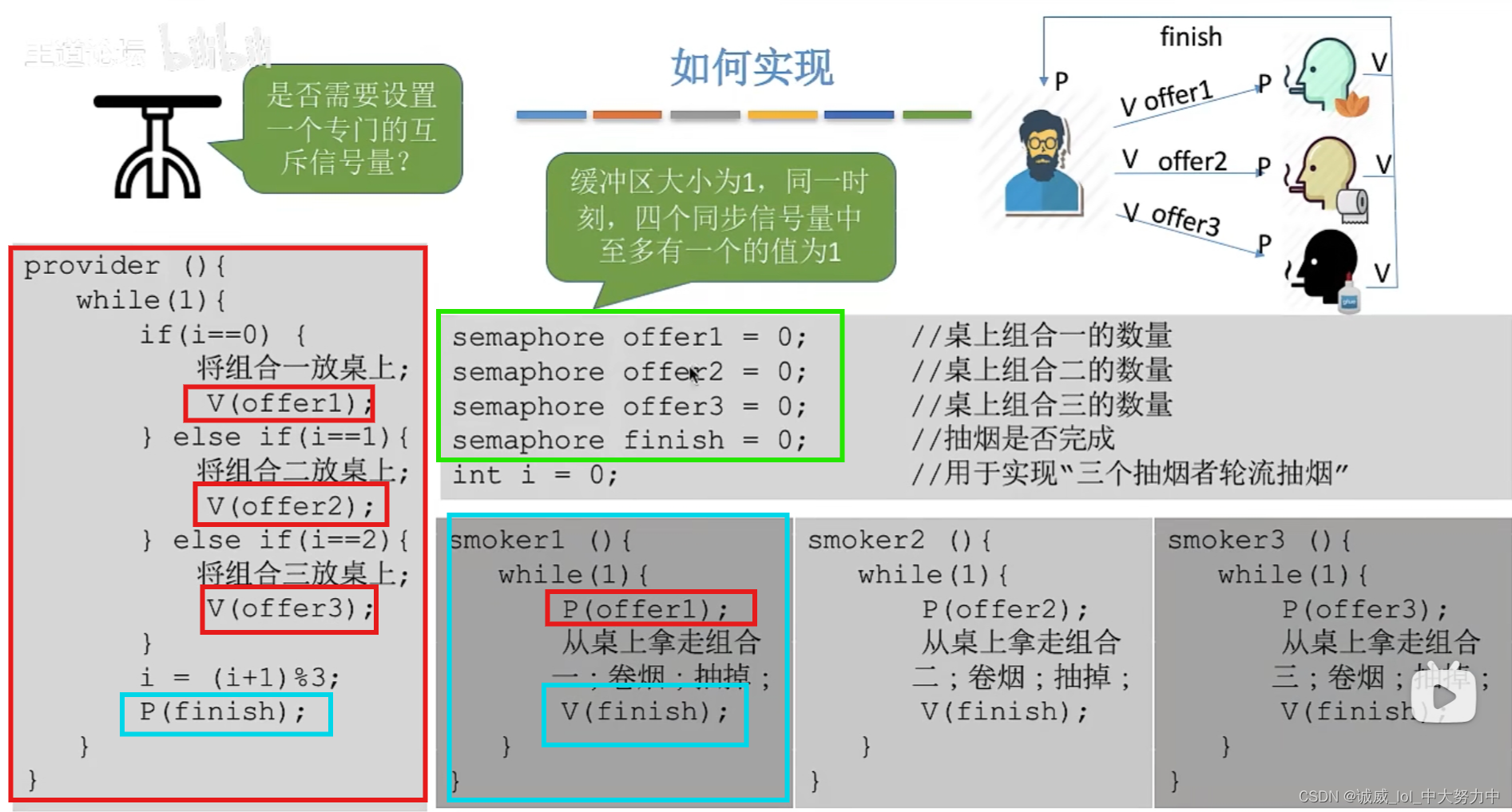
操作系统——吸烟者问题(王道视频p34、课本ch6)
1.问题分析:这个问题可以看作是 可以生产多种产品的 单生产者-多消费者问题 2.代码——这里就是由于同步信号量的初值都是1,所以没有使用mutex互斥信号, 总共4个同步信号量,其中一个是 finish信号量...
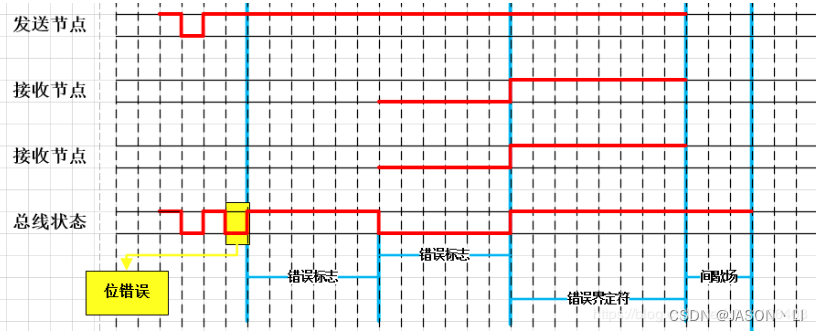
通讯协议学习之路:CAN协议理论
通讯协议之路主要分为两部分,第一部分从理论上面讲解各类协议的通讯原理以及通讯格式,第二部分从具体运用上讲解各类通讯协议的具体应用方法。 后续文章会同时发表在个人博客(jason1016.club)、CSDN;视频会发布在bilibili(UID:399951374) 序、…...

Redis常用配置详解
目录 一、Redis查看当前配置命令二、Redis基本配置三、RDB全量持久化配置(默认开启)四、AOF增量持久化配置五、Redis key过期监听配置六、Redis内存淘汰策略七、总结 一、Redis查看当前配置命令 # Redis查看当前全部配置信息 127.0.0.1:6379> CONFIG…...

卷积神经网络CNN学习笔记-MaxPool2D函数解析
目录 1.函数签名:2.学习中的疑问3.代码 1.函数签名: torch.nn.MaxPool2d(kernel_size, strideNone, padding0, dilation1, return_indicesFalse, ceil_modeFalse) 2.学习中的疑问 Q:使用MaxPool2D池化时,当卷积核移动到某位置,该卷积核覆盖区域超过了输入尺寸时,MaxPool2D会…...

基于图像字典学习的去噪技术研究与实践
图像去噪是计算机视觉领域的一个重要研究方向,其目标是从受到噪声干扰的图像中恢复出干净的原始图像。字典学习是一种常用的图像去噪方法,它通过学习图像的稀疏表示字典,从而实现对图像的去噪处理。本文将详细介绍基于字典学习的图像去噪技术…...
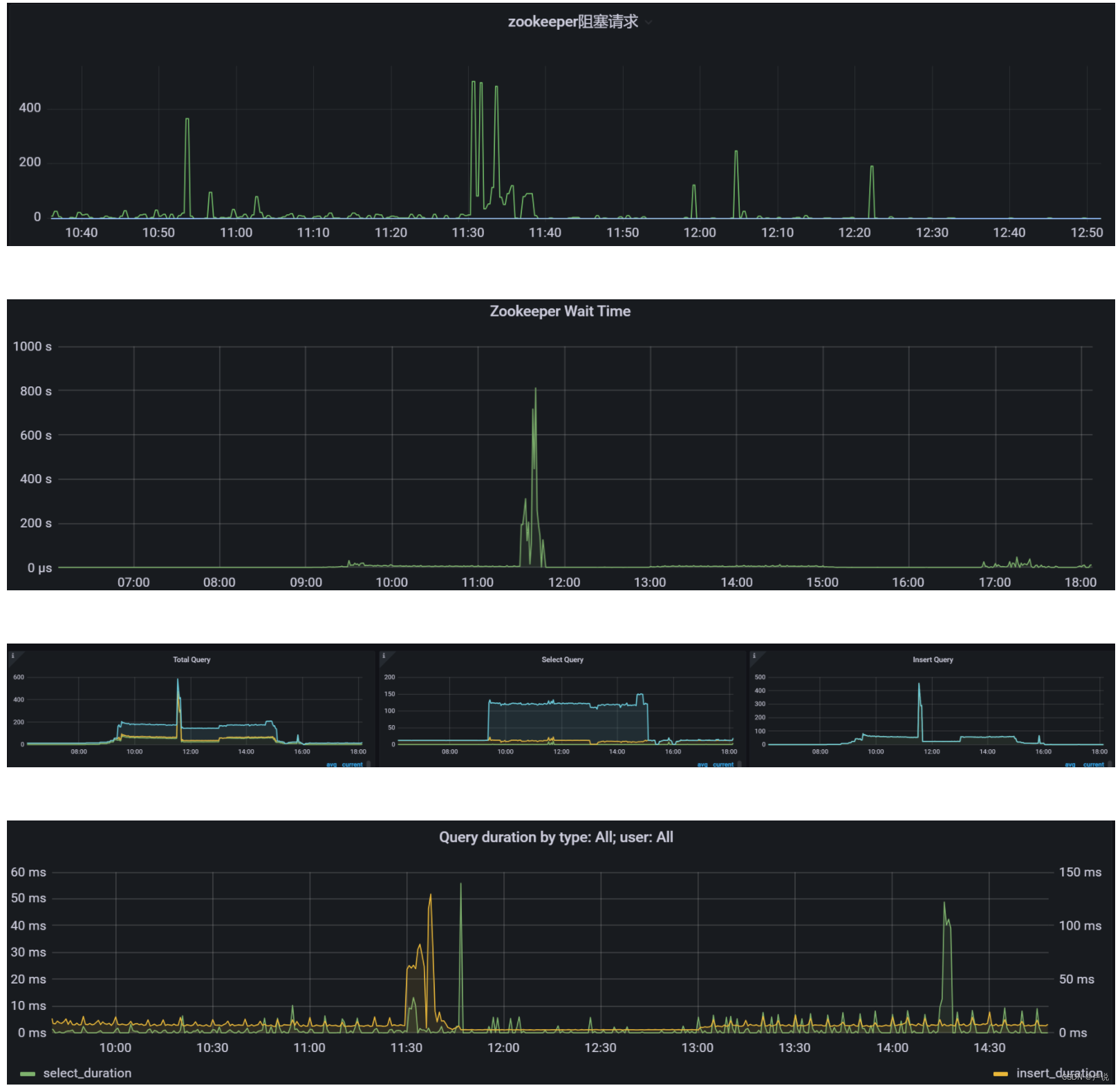
记一次Clickhouse 复制表同步延迟排查
现象 数据从集群中一个节点写入之后,其他两个节点无法及时查询到数据,等了几分钟。因为我们ck集群是读写分离架构,也就是一个节点写数据,其他节点供读取。 排查思路 从业务得知,数据更新时间点为:11:30。…...

Maven的详细安装步骤说明
Step 1: 下载Maven 首先,您需要从Maven官方网站(https://maven.apache.org/)下载Maven的最新版本。在下载页面上,找到与您操作系统对应的二进制文件(通常是.zip或.tar.gz格式),下载到本地。 St…...
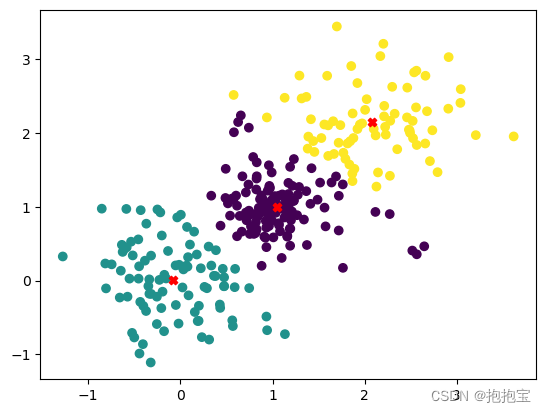
金融机器学习方法:K-均值算法
目录 1.算法介绍 2.算法原理 3.python实现示例 1.算法介绍 K均值聚类算法是机器学习和数据分析中常用的无监督学习方法之一,主要用于数据的分类。它的目标是将数据划分为几个独特的、互不重叠的子集或“集群”,以使得同一集群内的数据点彼此相似&…...

移远通信携手MIKROE推出搭载LC29H系列模组的Click boards开发板,为物联网应用带来高精定位服务
近日,移远通信与MikroElektronika(以下简称“MIKROE”)展开合作,基于移远LC29H系列模组推出了多款支持实时动态载波相位差分技术(RTK)和惯性导航(DR)技术的Click Boards™ 开发板&am…...
Spring Cloud 之 Sentinel简介与GATEWAY整合实现
简介 随着微服务的流行,服务和服务之间的稳定性变得越来越重要。Sentinel 是面向分布式服务架构的流量控制组件,主要以流量为切入点,从限流、流量整形、熔断降级、系统负载保护、热点防护等多个维度来帮助开发者保障微服务的稳定性。 熔断 …...

搭建网站七牛云CDN加速配置
打开七牛云后台;添加域名; 添加需要加速的域名,比如我添加的是motoshare.cn 源站配置,这里要用IP地址,访问的目录下面要有能访问测试的文件,尽量不要用源站域名,这个只能用加速二级域名&#x…...

算法|每日一题|做菜顺序|贪心
1402. 做菜顺序 原题地址: 力扣每日一题:做菜顺序 一个厨师收集了他 n 道菜的满意程度 satisfaction ,这个厨师做出每道菜的时间都是 1 单位时间。 一道菜的 「 like-time 系数 」定义为烹饪这道菜结束的时间(包含之前每道菜所花…...
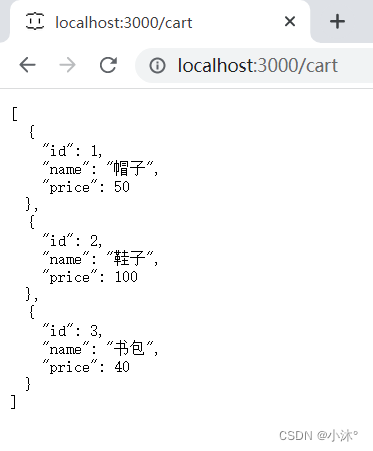
json-server工具准备后端接口服务环境
1.安装全局工具json-server(全局工具仅需要安装一次) 官网:json-server - npm 点击Getting started可以查看使用方法 在终端中输入yarn global add json-server或npm i json-server -g 如果输入json-server -v报错 再输入npm install -g j…...

文心一言 VS 讯飞星火 VS chatgpt (118)-- 算法导论10.3 3题
三、用go语言,在ALLOCATE-OBJECT和 FREE-OBJECT过程的实现中,为什么不需要设置或重置对象的 prev 属性呢? 文心一言: 在 Go 语言中,ALLOCATE-OBJECT 和 FREE-OBJECT 过程的实现通常不需要显式地设置或重置对象的 prev 属性。这…...

numpy矩阵画框框
在n>5(n是奇数)的nn数组中,用*画外方框和内接菱形。 (本笔记适合熟悉numpy的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”教程《 python 完全自学教程》,不仅仅是基础那…...

三十六、【进阶】show profiles分析
1、profiles (1)详情 可以帮助清楚的展现,每一条SQL语句的执行耗时,以及时间都耗费到哪里去了 (2)基础语句 2、查看是否支持profiles mysql> select have_profiling; ------------------ | have_prof…...
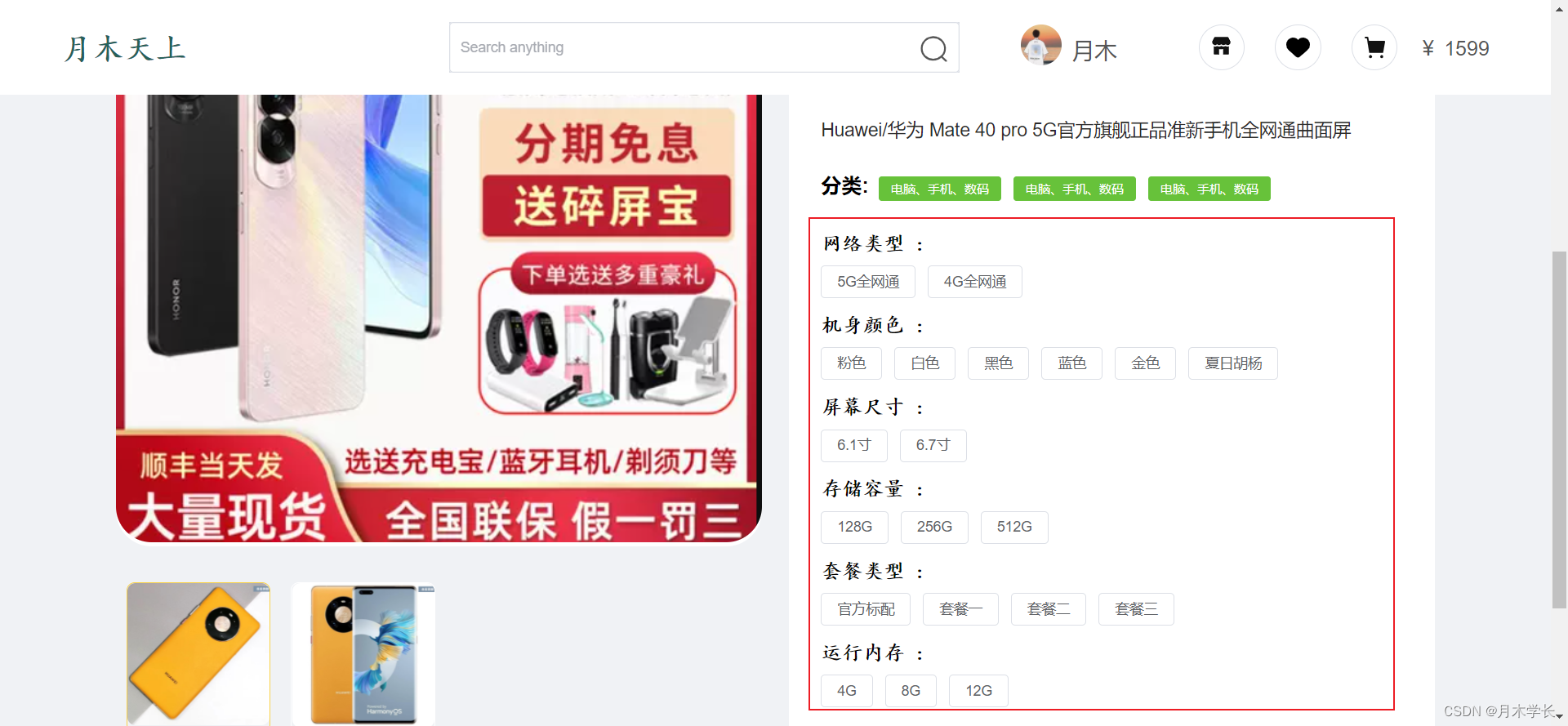
商品规格项数据的遍历以及添加
简介 今天在处理规格项的数据时遇到了一些问题,接下来就给大家分享一下 规格项数据设计 "specifications": [{"goodsSpecificationId": 6,"goodsSpecificationName": "网络类型","goodsTypeId": 24,"goods…...
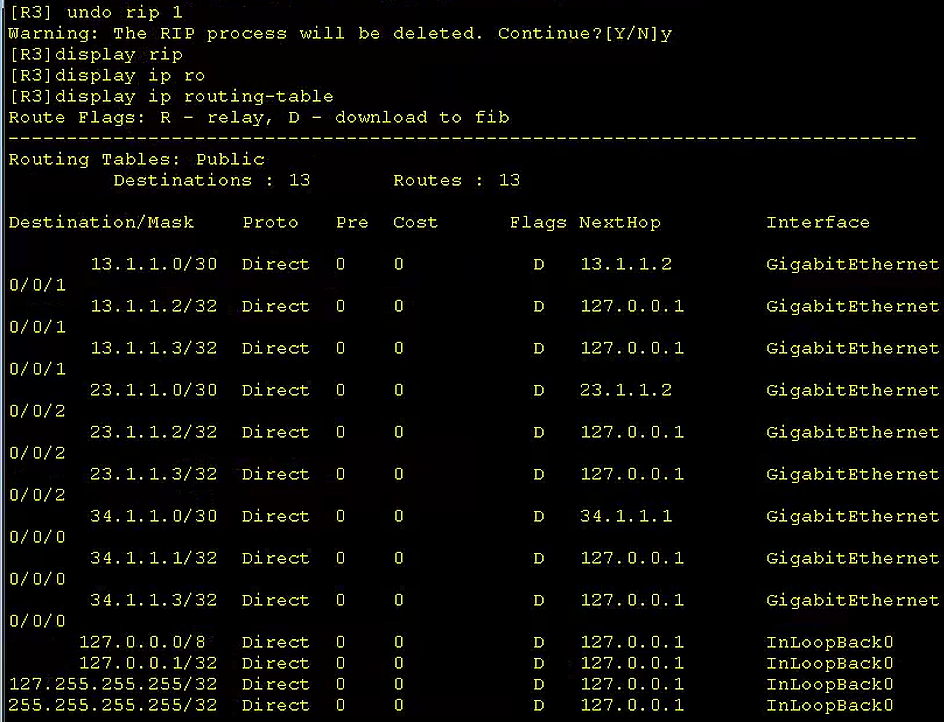
华为eNSP配置专题-RIP路由协议的配置
文章目录 华为eNSP配置专题-RIP路由协议的配置0、概要介绍1、前置环境1.1、宿主机1.2、eNSP模拟器 2、基本环境搭建2.1、终端构成和连接2.2、终端的基本配置 3、RIP路由的配置3.1、RIP路由的配置3.2、RIP路由的删除 华为eNSP配置专题-RIP路由协议的配置 0、概要介绍 路由信息…...

【软考】软件开发中不同对象之间的关系
1. 关联(Association): 关联表示两个或多个对象之间的关系。这种关系可以是双向的,也可以是单向的。关联关系通常用于描述两个对象之间的连接,但不涉及对象之间的所有权或整体-部分的关系。 例子: 考虑一…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
