力扣100114. 元素和最小的山形三元组 II(中等)
题目描述:
给你一个下标从 0 开始的整数数组 nums 。
如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 :
i < j < knums[i] < nums[j]且nums[k] < nums[j]
请你找出 nums 中 元素和最小 的山形三元组,并返回其 元素和 。如果不存在满足条件的三元组,返回 -1 。
示例 1:
输入:nums = [8,6,1,5,3] 输出:9 解释:三元组 (2, 3, 4) 是一个元素和等于 9 的山形三元组,因为: - 2 < 3 < 4 - nums[2] < nums[3] 且 nums[4] < nums[3] 这个三元组的元素和等于 nums[2] + nums[3] + nums[4] = 9 。可以证明不存在元素和小于 9 的山形三元组。
示例 2:
输入:nums = [5,4,8,7,10,2] 输出:13 解释:三元组 (1, 3, 5) 是一个元素和等于 13 的山形三元组,因为: - 1 < 3 < 5 - nums[1] < nums[3] 且 nums[5] < nums[3] 这个三元组的元素和等于 nums[1] + nums[3] + nums[5] = 13 。可以证明不存在元素和小于 13 的山形三元组。
示例 3:
输入:nums = [6,5,4,3,4,5] 输出:-1 解释:可以证明 nums 中不存在山形三元组。
提示:
3 <= nums.length <= 1051 <= nums[i] <= 108
思路:
题目的意思是求元素和最小 的山形三元组,而且这三个数满足:
i < j < knums[i] < nums[j]且nums[k] < nums[j]
也就是说中间那个数大于左右两边就行。
k的范围是1-nums.size()-2,我们遍历数组下标为1-nums.size()-2,当前的nums[i]表示的是山形三元组最中间的那个数,由于答案求元素和最小 ,每次遍历nums[i],都去找i前面最小的数,再去找i后面最小的数,这样求得的和对于nums[i]做山形三元组中间的数的所有三元组的和来说是最小的,遍历整个数组再对这个和取min就是答案了。
为什么这样求得的ans会是所有山形三元组的和的最小值呢?假设a[i]表示下标为i的元素作为山形三元组中间元素的最小和,a[i]=nums[i]+左边最小的数+右边最小的数,ans=min(a[i],ans).
所以ans是所有可能答案中的最小值。
代码:
class Solution {
public:int minimumSum(vector<int>& nums) {int len=nums.size();int lmi=nums[0];//左边最小的值vector<int> s(len+10);s[len-1]=nums[len-1];for(int i=len-2;i>=0;i--){s[i]=min(nums[i],s[i+1]);}//s[i]表示的是i-len-1的最小值int ans=1e9;for(int i=1;i<len-1;i++){if(nums[i]>lmi&&nums[i]>s[i+1]){ans=min(ans,nums[i]+lmi+s[i+1]);}lmi=min(lmi,nums[i]);//更新左边最小值}if(ans==1e9)return -1;//如果ans没有更新,说明不存在三元组return ans;}
};相关文章:
)
力扣100114. 元素和最小的山形三元组 II(中等)
题目描述: 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 : i < j < knums[i] < nums[j] 且 nums[k] < nums[j] 请你找出 nums 中 元素和最小 的山形三元组…...
--lcdseg - 段式lcd)
LuatOS-SOC接口文档(air780E)--lcdseg - 段式lcd
常量 常量 类型 解释 lcdseg.BIAS_STATIC number 没偏置电压(bias) lcdseg.BIAS_ONEHALF number 1/2偏置电压(bias) lcdseg.BIAS_ONETHIRD number 1/3偏置电压(bias) lcdseg.BIAS_ONEFOURTH number 1/4偏置电压(bias) lcdseg.DUTY_STATIC number 100%占空比(d…...

实现图像处理和分析的关键技术
在计算机视觉中,我们可以利用摄像头捕捉到的图像来进行各种分析和处理。以下是一些常见的计算机视觉任务: 对象检测:识别图像中的特定对象并标注其位置。人脸识别:识别和验证人脸身份。姿态估计:估计人体的姿态和动作…...

【C++学习笔记】内联函数
1. 概念 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调 用建立栈帧的开销,内联函数提升程序运行的效率。 如果在上述函数前增加inline关键字将其改成内联函数,在编译期间编译器会用函数…...
macOS Sonoma 14.1RC(23B73)发布
黑果魏叔10 月 18 日消息,苹果今日向 Mac 电脑用户推送了 macOS 14.1 RC更新(内部版本号:23B73),本次更新距离上次发布隔了 7 天。 macOS Sonoma 14.1RC(23B73)的更新内容主要包括以下方面&…...
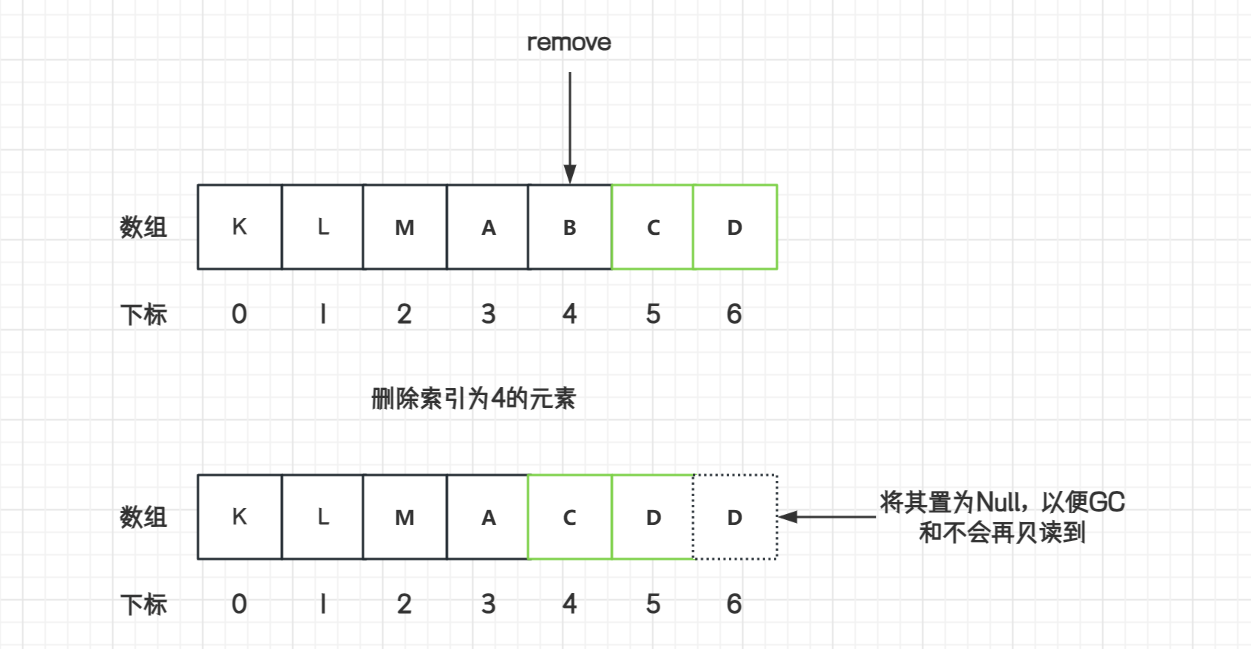
数据结构数组 Array 手写实现,扩容原理
数组数据结构 数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型数据的集合。 数组的特点: 数组是相同数据类型的元素集合(int 不能存放 double)数组中各元素的存储是有先…...
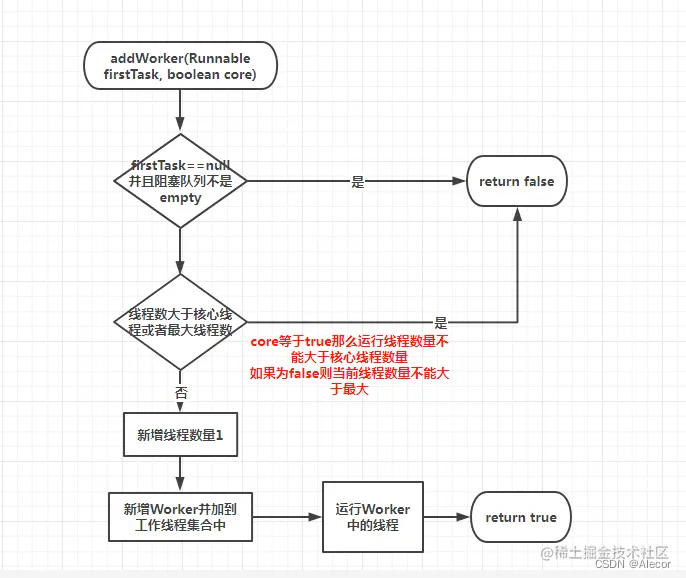
工作中几个问题的思考
对于需要并行多公司并行处理的任务,方案是什么? 多线程、并行流、并发库(ExecutorService、Futrue、Callable),分布式计算(1)按照公司ID分片 (2)按照业务类型分片 处理…...
Jmeter的性能测试
性能测试的概念 定义:软件的性能是软件的一种非功能特性,它关注的不是软件是否能够完成特定的功能,而是在完成该功能时展示出来的及时性。 由定义可知性能关注的是软件的非功能特性,所以一般来说性能测试介入的时机是在功能测试…...
IntelliJ IDEA 2020.2.1白票安装使用方法
先安装好idear Plugins 内手动添加第三方插件仓库地址:https://plugins.zhile.io 搜索:IDE Eval Reset插件进行安装 输入https://plugins.zhile.io 手动安装离线插件方法 安装包可以去笔者的CSDN资源库下载 安装mybaties插件...

【UCAS自然语言处理作业一】利用BeautifulSoup爬取中英文数据,计算熵,验证齐夫定律
文章目录 前言中文数据爬取爬取界面爬取代码 数据清洗数据分析实验结果 英文数据爬取爬取界面动态爬取 数据清洗数据分析实验结果 结论 前言 本文分别针对中文,英文语料进行爬虫,并在两种语言上计算其对应的熵,验证齐夫定律github: ShiyuNee…...

微信小程序之个人中心授权登录
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《Spring与Mybatis集成整合》《Vue.js使用》 ⛺️ 越努力 ,越幸运。 1.了解微信授权登录 微信登录官网: 小程序登录https://developers.weixin.qq.com/miniprogram/d…...
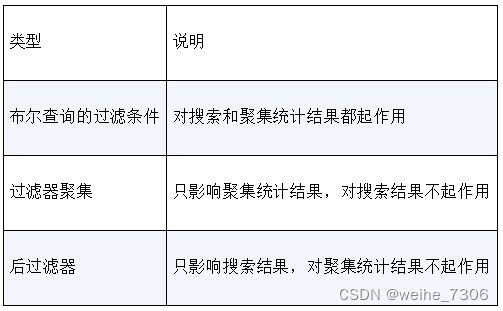
Elasticsearch的聚集统计,可以进行各种统计分析
说明: Elasticsearch不仅是一个大数据搜索引擎,也是一个大数据分析引擎。它的聚集(aggregation)统计的REST端点可用于实现与统计分析有关的功能。Elasticsearch提供的聚集分为三大类。 度量聚集(Metric aggregation):度量聚集可以用于计算搜…...

Webpack 理解 input output 概念
一、介绍 如果还没用过 Webpack 请先阅读 Webpack & 基础入门 再回头看本文。 Webpack 的核心只做两件事,输入管理(Input Management)和输出管理(Output Management),什么花里胡哨的插件和配置都离不…...

【字符函数】
✨博客主页:小钱编程成长记 🎈博客专栏:进阶C语言 🎈相关博文:字符串函数(一)、字符串函数(二) 字符函数 字符函数1.字符分类函数1.1 iscntrl - 判断是否是控制字符1.2 i…...
git创建与合并分支
文章目录 创建与合并分支分支管理的概念实际操作 解决冲突分支管理策略Bug分支Feature分支多人协作 创建与合并分支 分支管理的概念 分支在实际中有什么用呢?假设你准备开发一个新功能,但是需要两周才能完成,第一周你写了50%的代码…...

【电子通识】USB TYPE-A 2.0/3.0连接器接口
基础知识 USB TYPE-A连接器又可称为USB-A,现在不少PC、PC周边、手机充电器等等都依然采用了这种扁平的矩形接口,是目前普及度最高的USB接口了。 USB-A亦有分为插头与插座。常见的USB-A数据线的A端就是插头,而充电器上的则是插座。插头和插座…...

org.apache.sshd的SshClient客户端 连接服务器执行命令 示例
引入依赖 <dependency><groupId>org.apache.sshd</groupId><artifactId>sshd-core</artifactId><version>2.9.1</version></dependency>示例代码,可以直接执行,也可以做替换命令、维护session等修改 p…...

STM32 裸机编程 03
MCU 启动和向量表 当 STM32F429 MCU 启动时,它会从 flash 存储区最前面的位置读取一个叫作“向量表”的东西。“向量表”的概念所有 ARM MCU 都通用,它是一个包含 32 位中断处理程序地址的数组。对于所有 ARM MCU,向量表前 16 个地址由 ARM …...

Python ‘list‘ object is not callable错误
我尝试着解决“TypeError: ‘list’ object is not callable”这个错误。在Python编程中,我有时会遇到这个错误。这个错误通常是由于我错误地尝试像函数一样调用一个列表对象。为了解决这个问题,我需要找出错误发生的具体位置,然后进行修正。…...

原生php 实现redis登录五次被禁,隔天再登陆
<?php /*** Created by PhpStorm.* User: finejade* Date: 2023-10-18* Time: 11:08*/ session_start();include_once(header.php); include_once(connect.php); include_once(common.php); include_once(redis.php); try {// 常量 用户错误次数记录define("USER_LOGI…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
