nginx tomcat 动静分离
动静分离:
访问静态和动态页面分开
实现动态和静态页面负载均衡。
五台虚拟机
实验1,动静分离
思路:
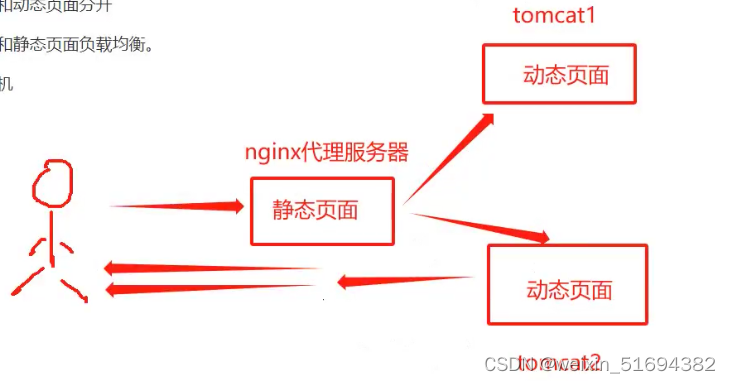
需要设备:三台虚拟机
一台nginx 代理又是静态
两台tomcat 请求动态页面
在全局模块中配置upstream tomcat

新建location
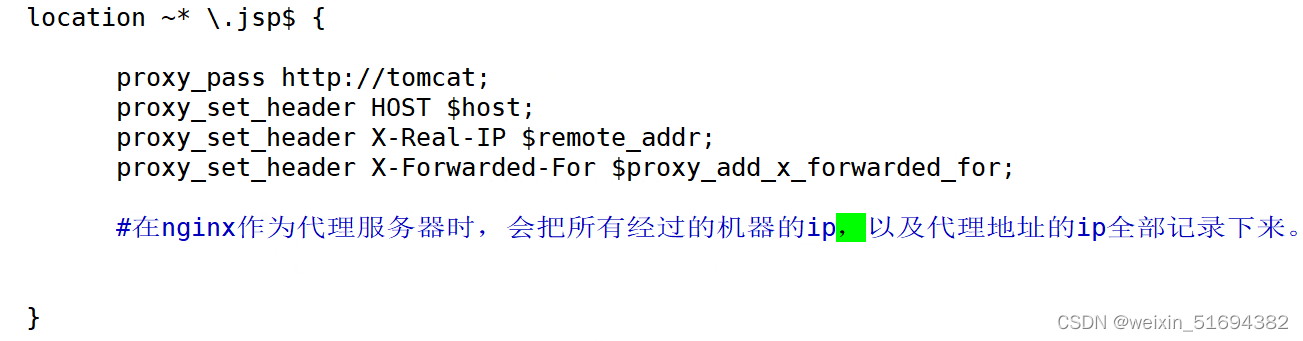
location ~ .*\.jsp$ {
proxy_pass http://tomcat;
proxy_set_header HOST $host;
proxy_set_header X-Real-IP $remote_addr;
proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
}
在html中配置前端页面

在tomcat 的server.xml 配置一个新的host文件,指定工作目录

实验2,四层加七层加动静分离
思路:
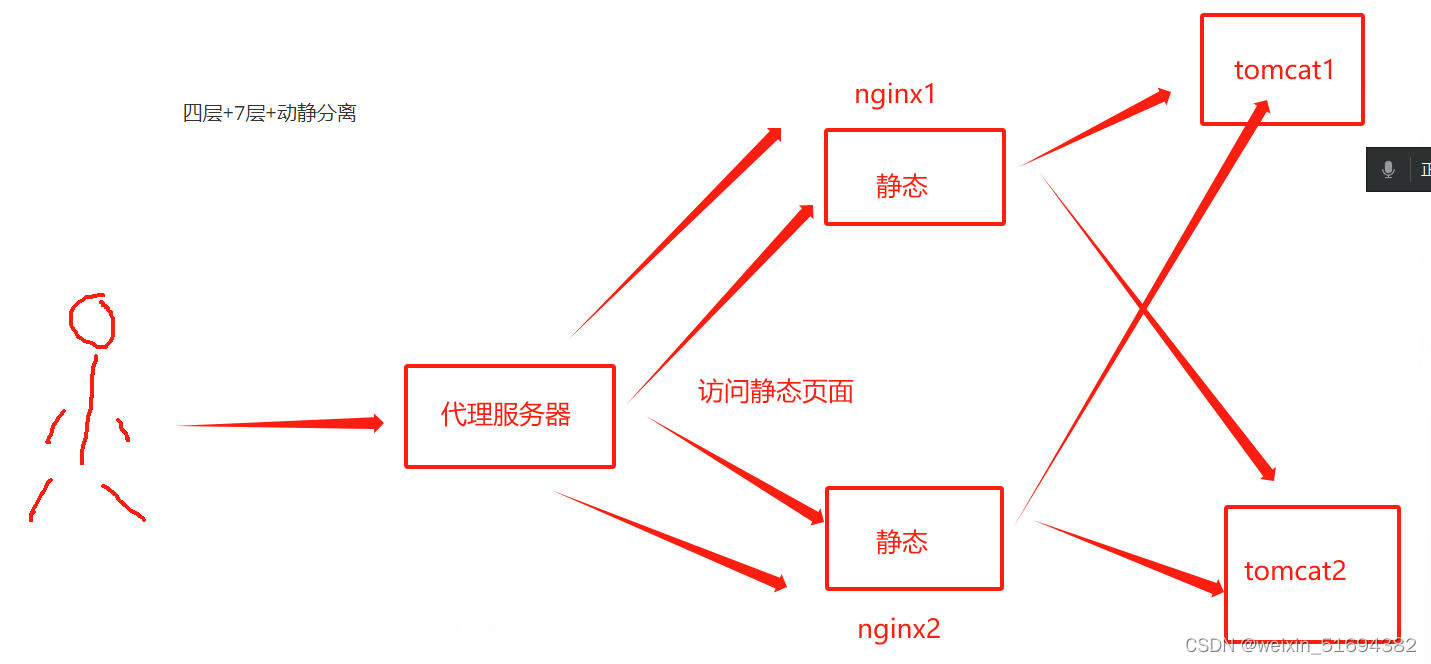
设备:
一台nginx代理
两台nginx做静态页面和动态请求服务转发器
两台tomcat做动态页面

1,在第一台nginx中配置stream ,只转发数据到两个静态页面

2,配置第一个代理服务器的前端页面
![]()
3,在后面两台nginx配置静态页面内容

4,再用这两台nginx做代理服务器指向动态页面

相关文章:

nginx tomcat 动静分离
动静分离: 访问静态和动态页面分开 实现动态和静态页面负载均衡。 五台虚拟机 实验1,动静分离 思路: 需要设备:三台虚拟机 一台nginx 代理又是静态 两台tomcat 请求动态页面 在全局模块中配置upstream tomcat 新建location…...

java读取指定文件夹下的全部文件,并输出文件名,文件大小,文件创建时间
import java.io.IOException; import java.nio.file.*; import java.nio.file.attribute.*; import java.util.ArrayList; import java.util.List; public class Main { public static void main(String[] args) { try { Path startingDir Paths.get("你的目…...

leetcode 105. 从前序与中序遍历序列构造二叉树
2023.10.21 本题需要根据前序遍历序列和中序遍历序列来构造出一颗二叉树。类似于从中序与后序遍历序列构造二叉树 。使用递归, java代码如下: /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* …...

【试题039】 多个逻辑或例题
题目:设int n;,执行表达式(n0)||(n1)||(n2)||(n3)后,n的值是?代码分析: //设int n; , 执行表达式(n 0) || (n 1) ||(n 2) ||(n 3)后, n的值是?int n;printf("n%d\n", (n 0) || (n 1) || (n 2) || (n 3));//分析࿱…...

打卡go学习第一天
8.1 下面展示一些 代码。 package mainimport ("fmt""net""os""time" )type Clock struct {Name stringAddr string } func main() {clocks : []Clock{{Name: "New York", Addr: "localhost:8000"…...

julia 笔记: 流程控制
1 复合表达式 用一个表达式有序地计算若干子表达式,并返回最后一个子表达式的值 1.1 begin代码块 z beginx 1y 2x yend z #3begin x 1; y 2; x y end #3 1.2 ;链 (x 1; y 2; x y) #3(x 1; y 2; x y) 3 2 条件表达式 x1 y2if x < yprintln(&q…...

【c++】 跟webrtc学周期性任务:tgcalls 5 网络超时检查
tgcalls 网络超时检查 G:\CDN\P2P-DEV\tdesktop-offical\Telegram\ThirdParty\tgcalls\tgcalls\NetworkManager.cppPostDelayedTask 使用的是rtc thread 方法 PostDelayedTask :G:\CDN\P2P-DEV\Libraries\tg_owt\src\rtc_base\thread.htemplate <class Closure,typename st…...

面试算法33:变位词组
题目 给定一组单词,请将它们按照变位词分组。例如,输入一组单词[“eat”,“tea”,“tan”,“ate”,“nat”,“bat”],这组单词可以分成3组,分别是[“eat”,“…...

【C语言】每日一题(旋转数组)
旋转数组,链接奉上 目录 方法:创建额外的数组:整体思路:代码实现: 数组反转:整体思路:代码实现:小插曲: 方法: 创建额外的数组: 整体思路: 创建一个额外的…...

系统架构师考试科目一:综合知识
某软件公司欲开发一个 Windows 平台上的公告板系统。在明确用户需求后,该公司的 架构师决定采用 Command 模式实现该系统的界面显示部分,并设计 UML 类图如下 图所示。图中与 Command 模式中的 Invoker 角色相对应的类是( ) ,与 ConcreteComm…...

面向对象与面向过程讲解
目录 简介 面向过程编程(Procedural Programming) 什么是面向过程编程? 特点: 面向对象编程(Object-Oriented Programming) 什么是面向对象编程? 特点: 面向对象 vs. 面向过程…...
】23 - QNX Ethernet MAC 驱动 之 emac1_config.conf 配置文件解析)
【SA8295P 源码分析 (四)】23 - QNX Ethernet MAC 驱动 之 emac1_config.conf 配置文件解析
【SA8295P 源码分析】23 - QNX Ethernet MAC 驱动 之 emac1_config.conf 配置文件解析 系列文章汇总见:《【SA8295P 源码分析 (四)】网络模块 文章链接汇总 - 持续更新中》 本文链接:《【SA8295P 源码分析 (四)】23 - QNX Ethernet MAC 驱动 之 emac1_config.conf 配置文件解…...

Python【list列表去重】
目录 要求: 将list中的重复数据去重,至少使用两种方案 方案一: 方案二: 要求: 将list中的重复数据去重,至少使用两种方案 方案一: 使用set ,可以将list转换为set࿰…...

Leetcode——字符
520. 检测大写字母 class Solution { public:bool detectCapitalUse(string word) {int big 0, small 0, len word.length();for (int i 0; i < len; i) {if (word[i] > 65 && word[i] < 90) {big;}else {small;}}if (big len || small len) {return tr…...
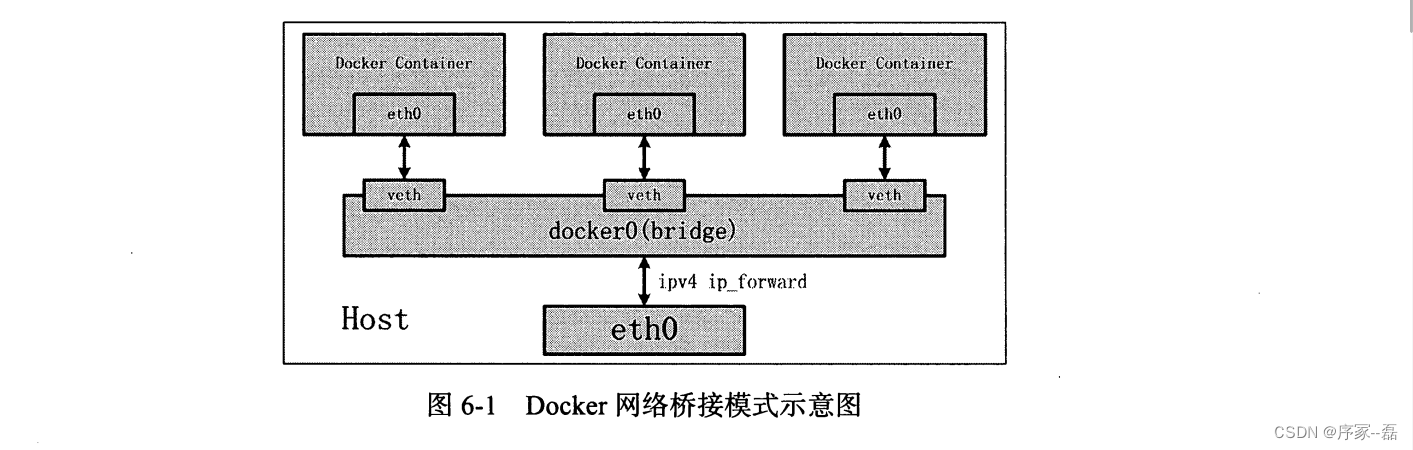
深入解析docker内核网桥
今天做虚拟桌面,朋友问我,为什么vnc 连接另一个docker 容器一直超时,原因是在docker 启动的时候没有组网,那么接下来我就要解析下docker的内核网络。 我们思考几个问题,带你了解linux 中docker 网络实现的基本原理。 文…...

ubuntu18.04服务器双网口配置上外网
记录一下配置服务器过程,本以为简单,结果整了一天。 服务器有2个网口,网口2是用来上外网的,原来用的01-netcfg.yaml进行ip地址设置,主要就用2条命令: vi /etc/netplan/01-netcfg.yaml (打开后…...

【安全体系架构】——防御深度架构
防御深度架构: 防御深度架构是一种多层次的安全模型,旨在通过在网络和系统的各个层次上部署多个安全措施,以抵御不同类型的威胁和攻击。这个模型承认单一的安全措施可能无法全面防御所有潜在威胁,因此采用了多层次的安全防御策略…...

Opencv之RANSAC算法用于直线拟合及特征点集匹配详解
Opencv之RANSAC算法用于直线拟合及特征点集匹配详解 讲述Ransac拟合与最小二乘在曲线拟合上的优缺点 讲述在进行特征点匹配时,最近邻匹配与Ransac匹配的不同之处 另外,Ransac也被用于椭圆拟合、变换矩阵求解等 1. 直线拟合 1.1 原理 RANSAC(RANdom …...

Jenkins环境部署与任务构建
一、CI/CD 1、CI/CD 概念: CI/CD 是一种软件开发和交付方法,旨在加速应用程序的开发、测试和部署过程,以提高软件交付的质量和效率。 (1) 持续集成 (CI Continuous Integration): 持续集成是开发团队频繁集成其代码更改的过程。开发者将其…...
ES6 Class和Class继承
1.class的基本语法 class可以理解为是一个语法糖,将js只能通过构造函数创建实例的方法进行了补充 构造函数: function Person ({ name, age18 }) {this.name namethis.age age } new Person({name: 张三}) Class类: class Person {con…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
