自学SLAM(4)《第二讲:三维物体刚体运动》作业
前言

小编研究生的研究方向是视觉SLAM,目前在自学,本篇文章为初学高翔老师课的第二次作业。
文章目录
- 前言
- 1.熟悉 Eigen 矩阵运算
- 2.几何运算练习
- 3.旋转的表达
- 4.罗德里格斯公式的证明
- 5.四元数运算性质的验证
- 6.熟悉 C++11
1.熟悉 Eigen 矩阵运算
设线性⽅程 Ax = b,在 A 为⽅阵的前提下,请回答以下问题:
- 在什么条件下, x 有解且唯⼀?
- ⾼斯消元法的原理是什么?
- QR 分解的原理是什么?
- Cholesky 分解的原理是什么?
- 编程实现 A 为 100 × 100 随机矩阵时,⽤ QR 和 Cholesky 分解求 x 的程序。你可以参考本次课⽤到的 useEigen 例程。
1.当r(A)=r([A|b])=n时,也就是A满秩,A可逆,方程组有唯一解。
2.高斯消元法如图所示:

3.QR的分解原理如图所示:
4.Cholesky分解的原理如下图:
5. 编程实现 A 为 100 × 100 随机矩阵时,⽤ QR 和 Cholesky 分解求 x 的程序。你可以参考本次课⽤到的 useEigen 例程。提⽰:你可能需要参考相关的数学书籍或⽂章。请善⽤搜索引擎。 Eigen 固定⼤⼩矩阵最⼤⽀持到 50,所以你会⽤到动态⼤⼩的矩阵。
其实这题就是让我们自己建立一个AX=B,利用Eigen的内置函数求解X
代码如下:
#include <iostream>
using namespace std;
#include <ctime>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace Eigen;#define MATRIX_SIZE 100//宏定义int main(int argc, char **argv)
{//建立一个动态矩阵AMatrixXd A;//建立一个100*100的随机矩阵A A = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE); //保证A为正定矩阵,A=A*A的转置(正定)A = A * A.transpose(); //建立一个float类型的动态矩阵BMatrix<double, Dynamic, 1> B; //建立一个100*1的随机矩阵BB = MatrixXd::Random(MATRIX_SIZE, 1); //建立一个动态矩阵XMatrix<double, Dynamic, 1> X;//建立一个100*1的随机矩阵X X = MatrixXd::Random(MATRIX_SIZE, 1); //QR分解X = A.colPivHouseholderQr().solve(B); cout << "QR: X = " << X.transpose() << endl;//cholesky分解X = A.ldlt().solve(B); cout << "cholesky: X = " << X.transpose() << endl;return 0;
}
运行结果如下:
Eigen的语法规则,及其用法参考如下:
#include <iostream>
using namespace std;
#include <ctime>
// Eigen 部分
#include <Eigen/Core>
// 稠密矩阵的代数运算(逆,特征值等)
#include <Eigen/Dense>#define MATRIX_SIZE 50/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/int main( int argc, char** argv )
{// Eigen 中所有向量和矩阵都是Eigen::Matrix,它是一个模板类。它的前三个参数为:数据类型,行,列// 声明一个2*3的float矩阵Eigen::Matrix<float, 2, 3> matrix_23;// 同时,Eigen 通过 typedef 提供了许多内置类型,不过底层仍是Eigen::Matrix// 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>,即三维向量Eigen::Vector3d v_3d;// 这是一样的Eigen::Matrix<float,3,1> vd_3d;// Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero(); //初始化为零// 如果不确定矩阵大小,可以使用动态大小的矩阵Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > matrix_dynamic;// 更简单的Eigen::MatrixXd matrix_x;// 这种类型还有很多,我们不一一列举// 下面是对Eigen阵的操作// 输入数据(初始化)matrix_23 << 1, 2, 3, 4, 5, 6;// 输出cout << matrix_23 << endl;// 用()访问矩阵中的元素for (int i=0; i<2; i++) {for (int j=0; j<3; j++)cout<<matrix_23(i,j)<<"\t";cout<<endl;}// 矩阵和向量相乘(实际上仍是矩阵和矩阵)v_3d << 3, 2, 1;vd_3d << 4,5,6;// 但是在Eigen里你不能混合两种不同类型的矩阵,像这样是错的// Eigen::Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d;// 应该显式转换Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;cout << result << endl;Eigen::Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;cout << result2 << endl;// 同样你不能搞错矩阵的维度// 试着取消下面的注释,看看Eigen会报什么错// Eigen::Matrix<double, 2, 3> result_wrong_dimension = matrix_23.cast<double>() * v_3d;// 一些矩阵运算// 四则运算就不演示了,直接用+-*/即可。matrix_33 = Eigen::Matrix3d::Random(); // 随机数矩阵cout << matrix_33 << endl << endl;cout << matrix_33.transpose() << endl; // 转置cout << matrix_33.sum() << endl; // 各元素和cout << matrix_33.trace() << endl; // 迹cout << 10*matrix_33 << endl; // 数乘cout << matrix_33.inverse() << endl; // 逆cout << matrix_33.determinant() << endl; // 行列式// 特征值// 实对称矩阵可以保证对角化成功Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver ( matrix_33.transpose()*matrix_33 );cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;// 解方程// 我们求解 matrix_NN * x = v_Nd 这个方程// N的大小在前边的宏里定义,它由随机数生成// 直接求逆自然是最直接的,但是求逆运算量大Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );Eigen::Matrix< double, MATRIX_SIZE, 1> v_Nd;v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );clock_t time_stt = clock(); // 计时// 直接求逆Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;cout <<"time use in normal inverse is " << 1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC << "ms"<< endl;// 通常用矩阵分解来求,例如QR分解,速度会快很多time_stt = clock();x = matrix_NN.colPivHouseholderQr().solve(v_Nd);cout <<"time use in Qr decomposition is " <<1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;return 0;
}2.几何运算练习
下⾯我们来练习如何使⽤ Eigen/Geometry 计算⼀个具体的例⼦。 设有⼩萝⼘ 1⼀号和⼩萝⼘⼆号位于世界坐标系中。⼩萝⼘⼀号的位姿为: q1 = [0:55; 0:3; 0:2; 0:2]; t1 =[0:7;1:1; 0:2]T(q 的第⼀项为实部)。这⾥的 q 和 t 表达的是 Tcw,也就是世界到相机的变换关系。⼩萝⼘⼆号的位姿为 q2 = [−0:1; 0:3; −0:7; 0:2]; t2 = [−0:1; 0:4;0:8]T。现在,⼩萝⼘⼀号看到某个点在⾃⾝的坐标系下,坐标为 p1 = [0:5; −0:1; 0:2]T,求该向量在⼩萝⼘⼆号坐标系下的坐标。请编程实现此事,并提交你的程序。
提⽰:
- 四元数在使⽤前需要归⼀化。
- 请注意 Eigen 在使⽤四元数时的虚部和实部顺序。
- 参考答案为 p2 = [1:08228; 0:663509; 0:686957]T。你可以⽤它验证程序是否正确。
#include <iostream>
using namespace std;
#include <Eigen/Core>
#include <Eigen/Geometry>
using namespace Eigen;
int main(int argc, char ** argv)
{//创建小萝卜1和2的位姿q1和q2Quaterniond q1(0.55, 0.3, 0.2, 0.2), q2(-0.1, 0.3, -0.7, 0.2);//四元数归一化(高博的SLAM视屏中的代码解释没有归一化)q1.normalize();q2.normalize();//创建小萝卜1和2的另一个位姿量t1和t2Vector3d t1(0.7, 1.1, 0.2), t2(-0.1, 0.4, 0.8);//创建p1坐标Vector3d p1(0.5, -0.1, 0.2); //欧式变换矩阵Tc1w和Tc2wIsometry3d Tc1w(q1), Tc2w(q2);Tc1w.pretranslate(t1);// 把平移向量设成(t1)Tc2w.pretranslate(t2);// 把平移向量设成(t2)//计算p2Vector3d p2 = Tc2w*Tc1w.inverse()*p1;cout << p2.transpose() << endl;return 0;
}
运行结果如下,我们可以看到答案正确:
Eigen/四元数的语法规则,及其用法参考如下:
#include <iostream>
#include <cmath>
using namespace std;
#include <Eigen/Core>
// Eigen 几何模块
#include <Eigen/Geometry>/****************************
* 本程序演示了 Eigen 几何模块的使用方法
****************************/int main ( int argc, char** argv )
{// Eigen/Geometry 模块提供了各种旋转和平移的表示// 3D 旋转矩阵直接使用 Matrix3d 或 Matrix3fEigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();// 旋转向量使用 AngleAxis, 它底层不直接是Matrix,但运算可以当作矩阵(因为重载了运算符)Eigen::AngleAxisd rotation_vector ( M_PI/4, Eigen::Vector3d ( 0,0,1 ) ); //沿 Z 轴旋转 45 度cout .precision(3);cout<<"rotation matrix =\n"<<rotation_vector.matrix() <<endl; //用matrix()转换成矩阵// 也可以直接赋值rotation_matrix = rotation_vector.toRotationMatrix();// 用 AngleAxis 可以进行坐标变换Eigen::Vector3d v ( 1,0,0 );Eigen::Vector3d v_rotated = rotation_vector * v;cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;// 或者用旋转矩阵v_rotated = rotation_matrix * v;cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;// 欧拉角: 可以将旋转矩阵直接转换成欧拉角Eigen::Vector3d euler_angles = rotation_matrix.eulerAngles ( 2,1,0 ); // ZYX顺序,即roll pitch yaw顺序cout<<"yaw pitch roll = "<<euler_angles.transpose()<<endl;// 欧氏变换矩阵使用 Eigen::IsometryEigen::Isometry3d T=Eigen::Isometry3d::Identity(); // 虽然称为3d,实质上是4*4的矩阵T.rotate ( rotation_vector ); // 按照rotation_vector进行旋转T.pretranslate ( Eigen::Vector3d ( 1,3,4 ) ); // 把平移向量设成(1,3,4)cout << "Transform matrix = \n" << T.matrix() <<endl;// 用变换矩阵进行坐标变换Eigen::Vector3d v_transformed = T*v; // 相当于R*v+tcout<<"v tranformed = "<<v_transformed.transpose()<<endl;// 对于仿射和射影变换,使用 Eigen::Affine3d 和 Eigen::Projective3d 即可,略// 四元数// 可以直接把AngleAxis赋值给四元数,反之亦然Eigen::Quaterniond q = Eigen::Quaterniond ( rotation_vector );cout<<"quaternion = \n"<<q.coeffs() <<endl; // 请注意coeffs的顺序是(x,y,z,w),w为实部,前三者为虚部// 也可以把旋转矩阵赋给它q = Eigen::Quaterniond ( rotation_matrix );cout<<"quaternion = \n"<<q.coeffs() <<endl;// 使用四元数旋转一个向量,使用重载的乘法即可v_rotated = q*v; // 注意数学上是qvq^{-1}cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;return 0;
}
3.旋转的表达

1. 设有旋转矩阵 R,证明 RT R = I 且 det R = +12。

2. 设有四元数 q,我们把虚部记为ε,实部记为 η,那么 q = (ε,η)。请说明 ε 和 η 的维度。
四元数q有三个虚部和一个实部。
即q=q0+q1i+q2j+q3k
因此ε的维度为3, η的维度为1。
3.第三问

4.罗德里格斯公式的证明
罗德⾥格斯公式描述了从旋转向量到旋转矩阵的转换关系。设旋转向量长度为 θ,⽅向为 n,那么旋转矩阵 R 为:
R = cos θI − (1 − cos θ)nnT + sin θn^. ------------------------------------------------------------(4)
我们在课程中仅指出了该式成⽴,但没有给出证明。请你证明此式。

参考:
链接: 罗德里格斯公式的证明
5.四元数运算性质的验证


6.熟悉 C++11
请注意本题为附加题。 C++ 是⼀门古⽼的语⾔,但它的标准⾄今仍在不断发展。在 2011 年、 2014 年和 2017 年, C++的标准又进⾏了更新,被称为 C++11, C++14, C++17。其中, C++11 标准是最重要的⼀次更新,让C++发⽣了重要的改变,也使得近年来的 C++ 程序与你在课本上(⽐如谭浩强)学到的 C++ 程序有很⼤的不同。你甚⾄会惊叹这是⼀种全新的语⾔。 C++14 和 C++17 则是对 11 标准的完善与扩充。
越来越多的程序开始使⽤11 标准,它也会让你在写程序时更加得⼼应⼿。本题中,你将学习⼀些 11标准下的新语法。请参考本次作业 books/⽬录下的两个pdf,并回答下⾯的问题。 设有类 A,并有 A 类的⼀组对象,组成了⼀个 vector。现在希望对这个 vector进⾏排序,但排序的⽅式由 A.index 成员⼤⼩定义。那么,在 C++11 的语法下,程序写成:
1#include <iostream>
2#include <vector>
3#include <algorithm>
4
5 using namespace std;
6
7 class A {
8 public:
9 A(const int& i ) : index(i) {}
10 int index = 0;
11};
12
13 int main() {
14 A a1(3), a2(5), a3(9);
15 vector<A> avec{a1, a2, a3};
16 std::sort(avec.begin(), avec.end(), [](const A&a1, const A&a2) {return a1.index<a2.index;});
17 for ( auto& a: avec ) cout<<a.index<<" ";
18 cout<<endl;
19 return 0;
20 }
请说明该程序中哪些地⽅⽤到了 C++11 标准的内容。提⽰:请关注范围 for 循环、⾃动类型推导、 lambda表达式等内容。
该程序中使用了C++11标准的以下内容:
iostream:使用了C++11中引入的iostream库,用于输入输出流操作。
vector:使用了C++11中引入的vector容器,用于存储和操作A类的实例。
algorithm:使用了C++11中引入的algorithm库,其中的sort函数用于对vector容器中的元素进行排序。
using namespace std;:使用了C++11中引入的namespace别名声明,用于简化对std命名空间的使用。
class A:使用了C++11中引入的类初始化列表语法,用于对A类的成员变量进行初始化。
vector avec{a1, a2, a3}; :使用了C++11中引入的列表初始化语法,用于初始化vector容器avec并添加元素。
[] (const A&a1, const A&a2) { return a1.index < a2.index; }:使用了C++11中引入的lambda表达式,用作sort函数的排序准则。其中:const A&a1, const A&a2是参数列表,return a1.index<a2.index;是函数体,返回值是布尔型的大小比较结果。
for (auto& a : avec):使用了C++11中引入的范围for循环语法,用于遍历vector容器avec中的元素。用auto关键字实现了自动类型推导,让编译器自动设置变量a的类型;C++引入了基于范围的for循环,不用下标就能访问元素;

相关文章:

自学SLAM(4)《第二讲:三维物体刚体运动》作业
前言 小编研究生的研究方向是视觉SLAM,目前在自学,本篇文章为初学高翔老师课的第二次作业。 文章目录 前言1.熟悉 Eigen 矩阵运算2.几何运算练习3.旋转的表达4.罗德里格斯公式的证明5.四元数运算性质的验证6.熟悉 C11 1.熟悉 Eigen 矩阵运算 设线性⽅程 …...
)
C++:容量适配器(栈、队列、优先级队列)
目录 1.容器适配器 4.1 什么是适配器 4.2 STL标准库中的容器适配器 2.stack的使用 2.1 STL库中对stack的实现 3.queue的使用 3.1 STL库中对queue的实现 4.priority_queue使用 4.1模拟实现 priority_queue 5.deque 的简介 1.容器适配器 4.1 什么是适配器 适配器是一种…...

Java-IO流
文章目录 Java-IO流文件字节流文件字符流File类缓冲流转换流打印流数据流对象流 Java-IO流 JDK提供了一套用于IO操作的框架,为了方便我们开发者使用,就定义了一个像水流一样,根据流的传输方向和读取单位,分为字节流InputStream和…...
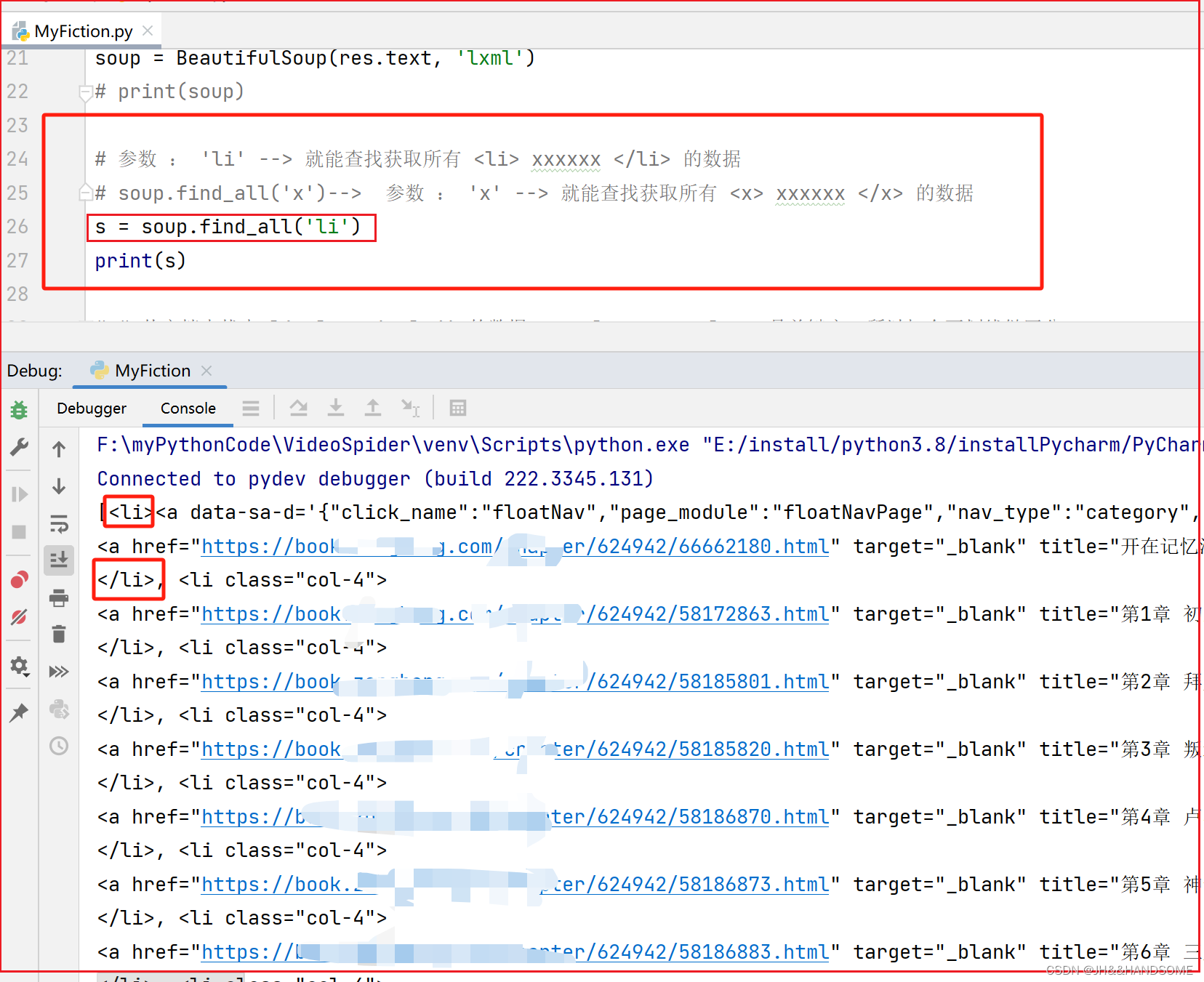
04、Python 爬取免费小说思路
目录 Python 爬取免费小说思路代码解析爬取东西基本的四行代码:user-agent安装模块从 bs4 导入 BeautifulSoup ,查询某个标签开头的数据筛选遍历获取小说的章节名称每章小说的链接获取请求网址的响应获取小说的内容筛选内容整理内容爬取下载到指定文件夹完整代码:Python 爬取…...
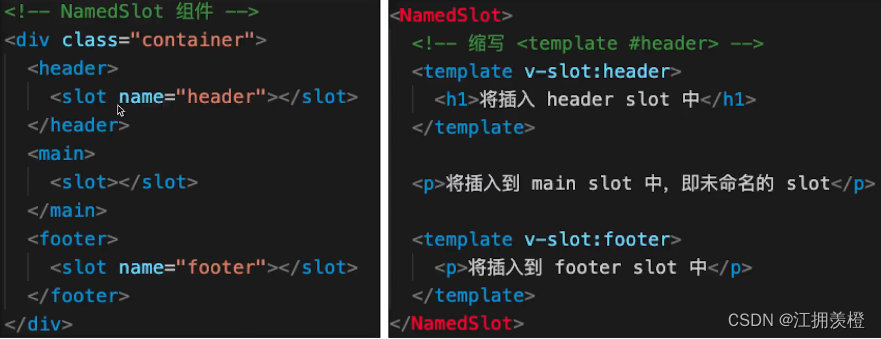
【前端vue面试】vue2
目录 computed和watchv-show和v-ifkey 的重要性v-for 和 v-if 不能一起使用!click的event修饰符事件修饰符表单项修饰符 父子组件通讯生命周期父子组件生命周期顺序 $nextTickslot 插槽动态组件异步组件keep-alivemixin computed和watch computed 有缓存࿰…...

自然语言处理---Transformer机制详解之GPT模型介绍
1 GPT介绍 GPT是OpenAI公司提出的一种语言预训练模型.OpenAI在论文<< Improving Language Understanding by Generative Pre-Training >>中提出GPT模型.OpenAI后续又在论文<< Language Models are Unsupervised Multitask Learners >>中提出GPT2模型.…...
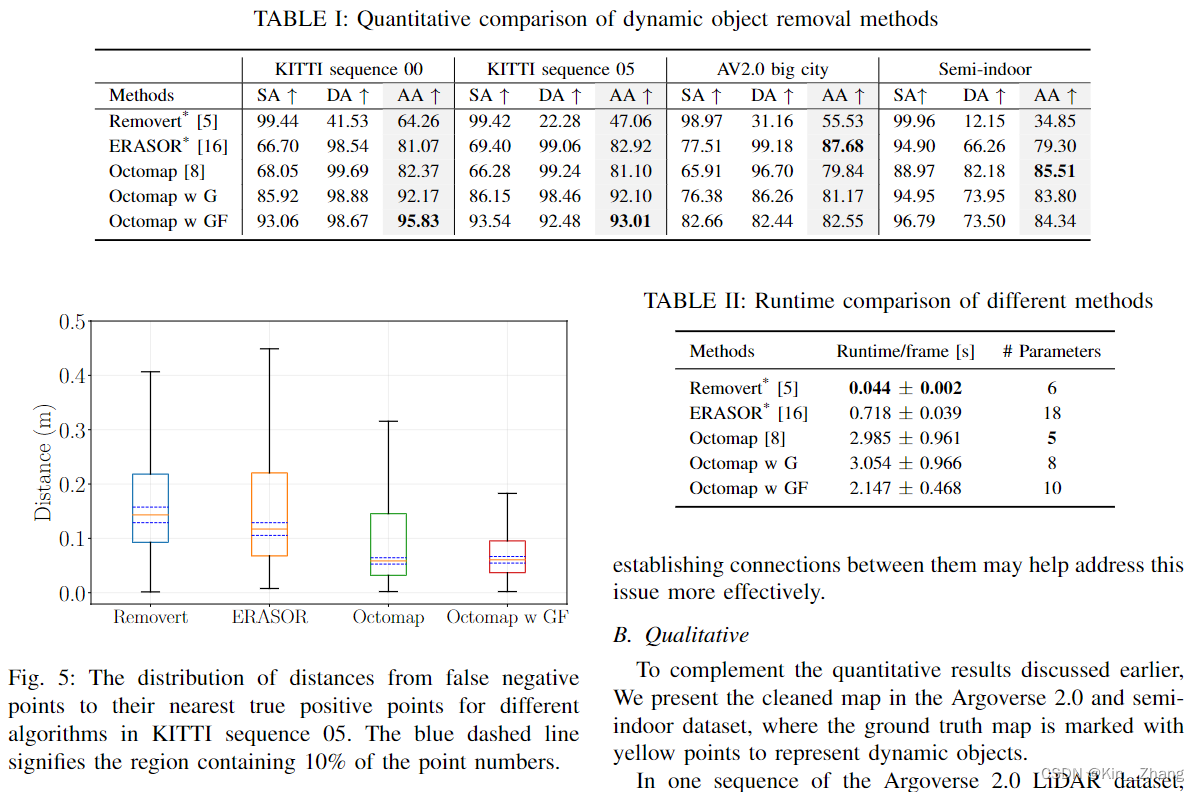
【论文阅读】点云地图动态障碍物去除基准 A Dynamic Points Removal Benchmark in Point Cloud Maps
【论文阅读】点云地图动态障碍物去除基准 A Dynamic Points Removal Benchmark in Point Cloud Maps 终于一次轮到了讲自己的paper了 hahaha,写个中文的解读放在博客方便大家讨论 Title Picture Reference and prenotes paper: https://arxiv.org/abs/2307.07260 …...
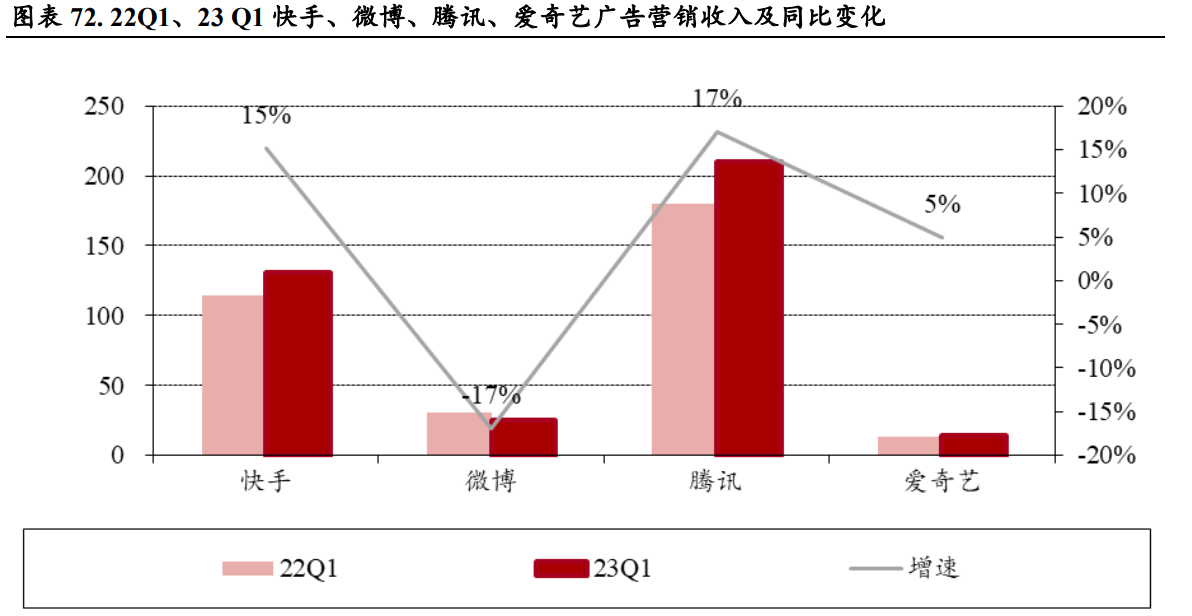
2023年传媒行业中期策略 AIGC从三个不同层次为内容产业赋能
基本面和新题材共振,推动传媒互联网行情上涨 AIGC 概念带动,传媒板块领涨 A 股 2023 年第一个交易日(1 月 3 日)至 6 月 2 日,申万传媒指数区间涨幅高达 48.38%,同时期沪深 300 跌幅为 0.25%,…...

iOS上架App Store的全攻略
iOS上架App Store的全攻略 第一步:申请开发者账号 在开始将应用上架到App Store之前,你需要申请一个开发者账号。 1.1 打开苹果开发者中心网站:https://developer.apple.com/ 1.2 使用Apple ID和密码登录(如果没有账号则需要注册…...
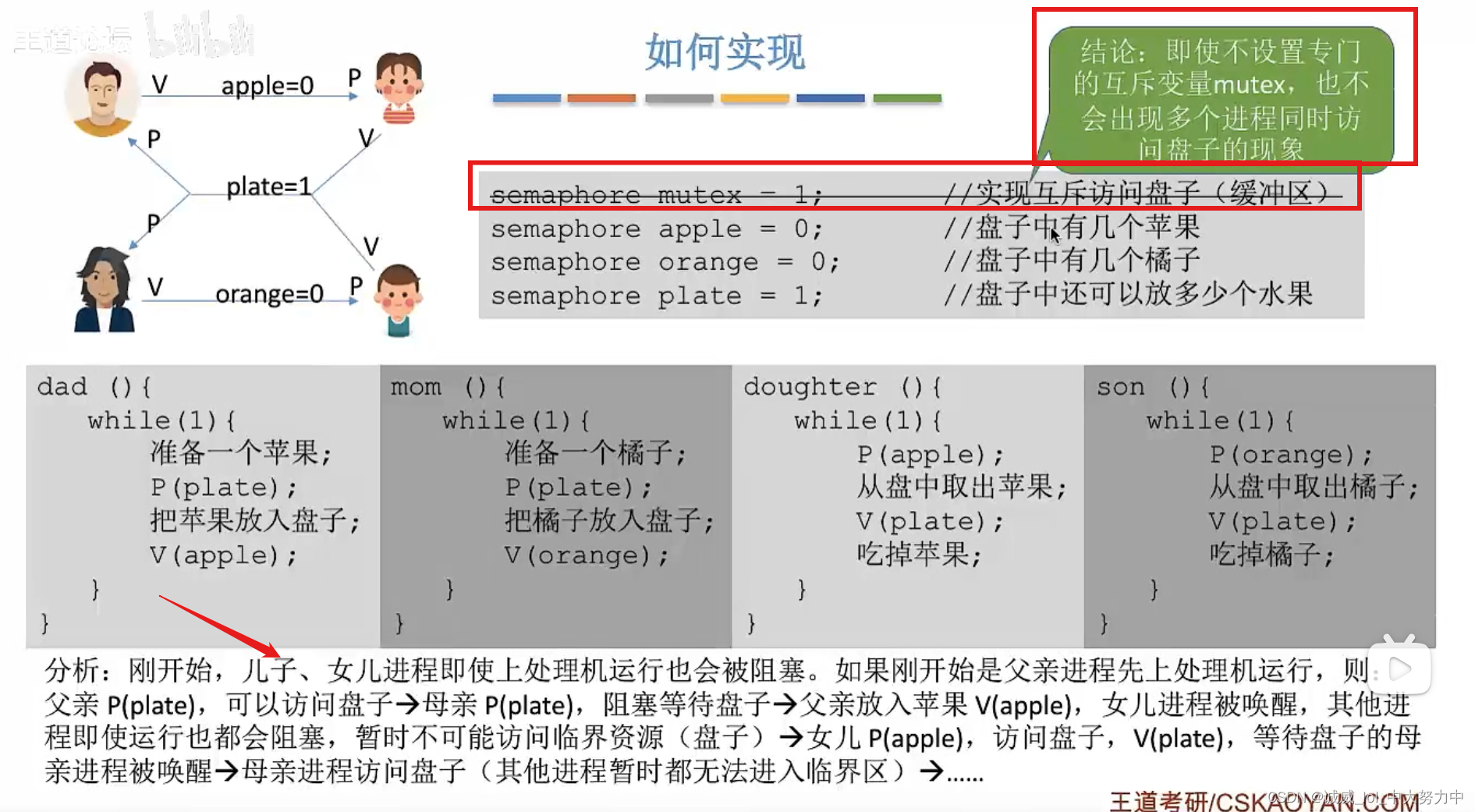
操作系统——多个类别产品的生产者-消费者问题(王道视频p33、课本ch6)
1.问题解剖——得到的是 1个“互斥信号量” 3个“同步信号量” 其中特别注意,对于盘子plate可以清空的设计4个对象的,但是只用这一个同步信号量就可以实现 2.代码—— 3.由于这里的同步信号量的初值都是1,所以,即使不设置互斥信…...
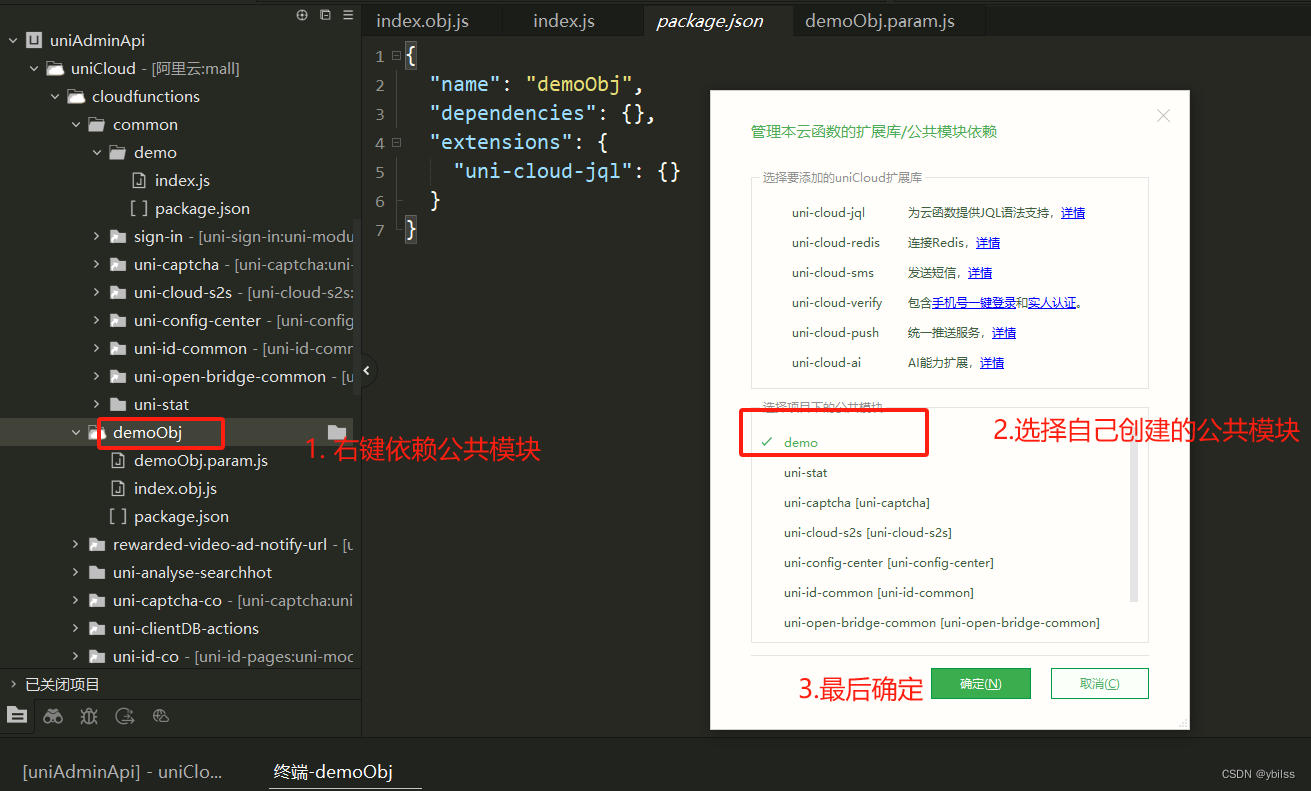
uniapp(uncloud) 使用生态开发接口详情5(云公共模块)
1.uniCloud官网 云对象中云公共模块: 网站: https://uniapp.dcloud.net.cn/uniCloud/cf-common.html // 官网介绍 cloudfunctions├─common // 云函数公用模块目录| └─hello-common // 云函数公用模块| ├─package.json| └─index.js // 公用模块代码࿰…...
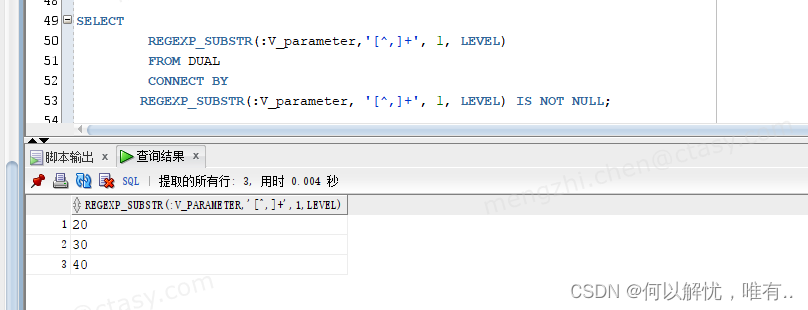
Oracle数据中如何在 where in() 条件传参
一、问题场景描述 在sql 条件中,如何在 where in()中想传入参数,如果直接 where in(:seqList),当传入单个值,seqList: ‘80’ 是没问题的,但是初入多个值时,seqList: ‘80,90’ ,因缺少单引号&…...

Python:函数篇(每周练习)
编程题: Python第四章作业(初级) (educoder.net) 题一:无参无返回值函数 def print_hi_human(): # 函数名用小写字母print("人类,你好!")if __name__ __main__:print_hi_human() 题二&#…...

为Element Plus封装业务组件FormDialog,将所有需要填写表单的弹窗组件封装,方便快速配置
使用FormDialog组件能够对表单弹窗进行快速配置,不用每次单独写弹窗表单业务组件,快速实现表单弹窗业务功能。 调用页面demo.vue validateRules.js引用 <script setup lang"ts"> import FormDialog from /components/FormDialog/index…...

ubuntu 设置和取消代理
背景 因为国内环境限制,在 linux 上安装一些软件的时候,因为限制就安装不了, 此时就可以通过设置代理的方式来规避这种问题,下面是具体的设置方式 步骤 sudo vim /etc/profile.d/proxy.sh添加以下内容到文件中 export http_pro…...
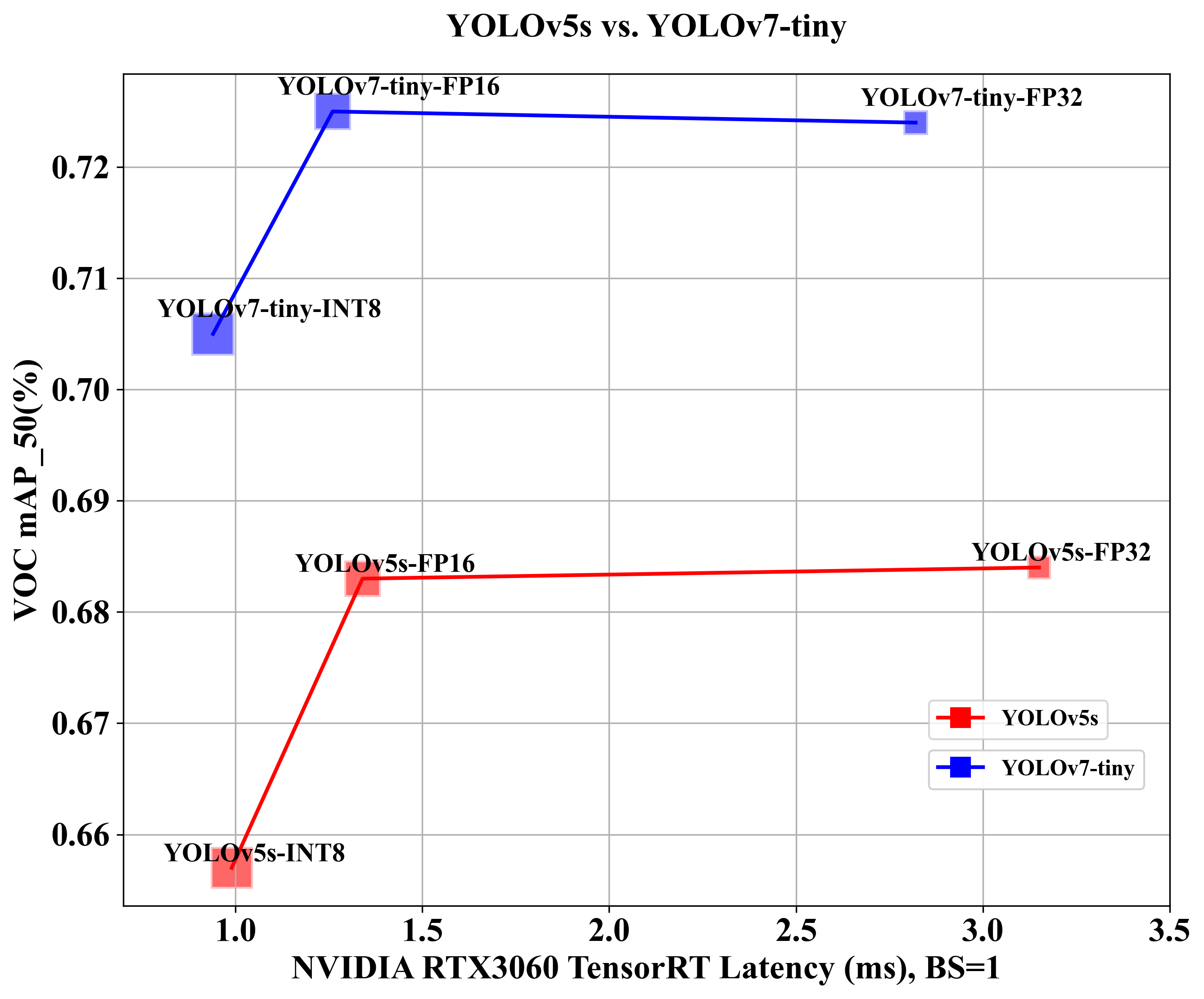
YOLOv7-PTQ量化部署
目录 前言一、PTQ量化浅析二、YOLOv7模型训练1. 项目的克隆和必要的环境依赖1.1 项目的克隆1.2 项目代码结构整体介绍1.3 环境安装 2. 数据集和预训练权重的准备2.1 数据集2.2 预训练权重准备 3. 训练模型3.1 修改模型配置文件3.2 修改数据配置文件3.3 训练模型3.4 mAP测试 三、…...
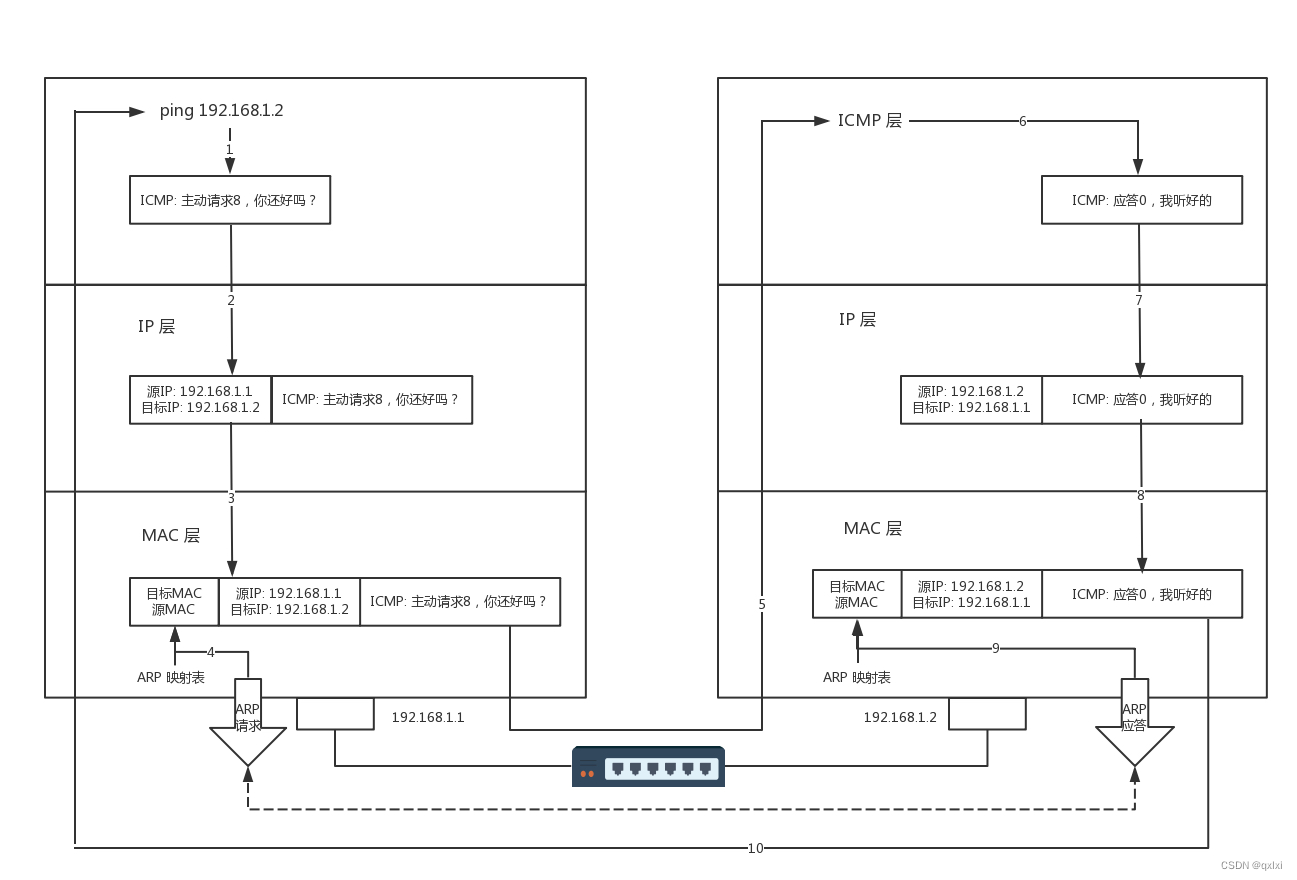
【网络协议】聊聊ICMP与ping是如何测试网络联通性
ICMP协议格式 ping是基于iCMP协议工作的,ICMP全称Internet Control Message Protocol,就是互联网控制报文协议。其实就是有点类似于古代行军打仗,哨探进行前方探明具体情况。 IMCP本身处于网络层,将报文封装在IP包里,…...

nginx tomcat 动静分离
动静分离: 访问静态和动态页面分开 实现动态和静态页面负载均衡。 五台虚拟机 实验1,动静分离 思路: 需要设备:三台虚拟机 一台nginx 代理又是静态 两台tomcat 请求动态页面 在全局模块中配置upstream tomcat 新建location…...

java读取指定文件夹下的全部文件,并输出文件名,文件大小,文件创建时间
import java.io.IOException; import java.nio.file.*; import java.nio.file.attribute.*; import java.util.ArrayList; import java.util.List; public class Main { public static void main(String[] args) { try { Path startingDir Paths.get("你的目…...

leetcode 105. 从前序与中序遍历序列构造二叉树
2023.10.21 本题需要根据前序遍历序列和中序遍历序列来构造出一颗二叉树。类似于从中序与后序遍历序列构造二叉树 。使用递归, java代码如下: /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* …...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
