[swift刷题模板] 树状数组(BIT/FenwickTree)
@[TOC]([swift刷题模板] 树状数组(BIT/FenwickTree) )
一、 算法&数据结构
1. 描述
- [python刷题模板] 树状数组
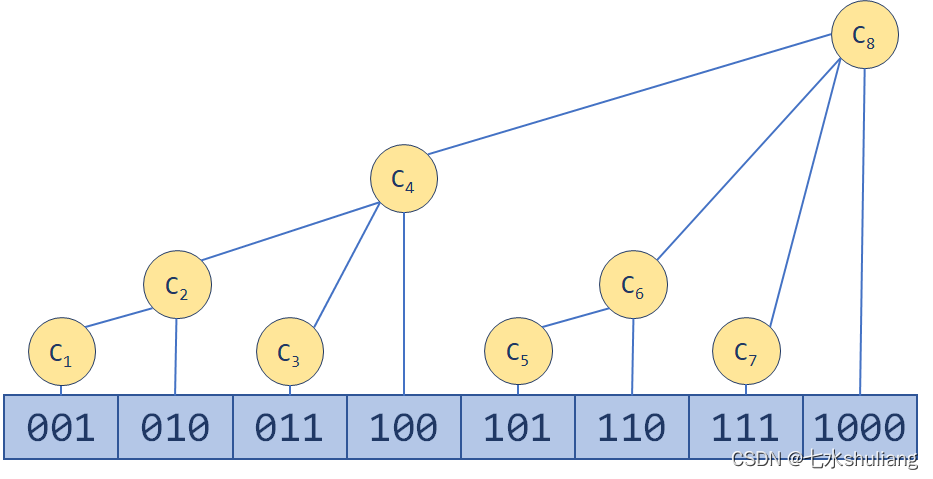
二、 模板代码
1. 单点赋值(增加),区间求和(PURQ)
例题: 307. 区域和检索 - 数组可修改
class BIT {var c: [Int]var n: Int init(_ n: Int){c = Array(repeating:0, count: n + 1)self.n = n }func add(_ i: Int, _ v: Int){var i = i while i <= n {c[i] += v i += i & -i }}func sum(_ i: Int) -> Int {var i = i var s = 0 while i > 0 {s += c[i] i &= i - 1}return s}
}class NumArray {let tree: BIT var nums: [Int]init(_ nums: [Int]) { tree = BIT(nums.count + 1)self.nums = nums for (i, v) in nums.enumerated() {tree.add(i + 1, v)}} func update(_ index: Int, _ val: Int) {tree.add(index+1, val - nums[index])nums[index] = val}func sumRange(_ left: Int, _ right: Int) -> Int {return tree.sum(right + 1) - tree.sum(left) }
}
- 以下待施工
2. 区间更新,单点询值(RUPQ)
例题: 1589. 所有排列中的最大和
这题其实应该用差分数组,可以省一层log。思想就是树状数组的IUPQ模型。
树状数组经典案例,要用差分数组理解:
这个实际上是用树状数组维护原数组的差分数组c[i]=a[i]-a[i-1]
求原数组的值a[i]实际上是差分数组的前缀sum(c[0]…c[i]),所以get a[i]可以用sum c[i]表示,
而原数组a区间[x,y]更新+v,产生的效果是:x位置比x-1位置大了v,y+1位置比y小了v;
对差分数组c来说,产生变化的就是c[x]增加了v,c[y+1]减小了v,因为c数组代表的是a中每个数比前一个数的差。
- sum[i]代替get[i],单点求值
- 两步add(l,v)和add(r+1,-v),区间更新
3.区间更新,区间求和(RURQ)
题目: P3372 【模板】线段树 1
- 记sigma(r,i)表示r数组的前i项和。
- 我们知道,在区间求和的BIT中,实际维护了原数组a的差分数组d。
- 于是有a[n] = d[1]+d[2]+…+d[n]
- 观察式子:
a[1]+a[2]+…+a[n]
= (d[1]) + (d[1]+d[2]) + … + (d[1]+d[2]+…+d[n])
= n * d[1] + (n-1) * d[2] +… +d[n]
= n * (d[1]+d[2]+…+d[n]) - (0 * d[1]+1 * d[2]+…+(n-1) * d[n])(式子①)
维护一个数组d2[n],其中d2[i] = (i-1)*d[i]
每当修改c的时候,就同步修改一下d2,这样复杂度就不会改变
那么 sigma(a,n) = 式子①=n*sigma(d,n) - sigma(d2,n)
5. 单点更新区间求极值
例题: CF522 D. Closest Equals
这是20220923的茶。
- 相同元素组成可以看成线段,问题转化为求区间内最短线段。
- 询问离线,按r排序,计算每个线段长度,记在左端点上。
- 查询区间最小值即可。
- 正常用线段树,但是py线段树过不了,于是上网查了个树状数组的模板
6. 单点赋值,区间询问最大(LIS II)
例题: 2407. 最长递增子序列 II
周赛T4,当时用线段树做的;实际测试线段树的表现甚至优于树状数组,奇怪极了。
7. 二维树状数组(IUPQ)
例题: 6292. 子矩阵元素加 1
- 周赛T2,这题卡一维树状数组;但是可以差分过;可以二维树状数或二维差分过。
相关文章:

[swift刷题模板] 树状数组(BIT/FenwickTree)
[TOC]([swift刷题模板] 树状数组(BIT/FenwickTree) ) 一、 算法&数据结构 1. 描述 [python刷题模板] 树状数组 二、 模板代码 1. 单点赋值(增加),区间求和(PURQ) 例题: 307. 区域和检索 - 数组可修改 class BIT {var c: [Int]var n: Int init(_ n: Int){c…...

CUDA学习笔记(三)CUDA简介
本篇博文转载于https://www.cnblogs.com/1024incn/tag/CUDA/,仅用于学习。 前言 线程的组织形式对程序的性能影响是至关重要的,本篇博文主要以下面一种情况来介绍线程组织形式: 2D grid 2D block 线程索引 矩阵在memory中是row-major线性…...
RK3568笔记三:基于ResNet18的Cifar-10分类识别训练部署
若该文为原创文章,转载请注明原文出处。 本篇文章参考的是野火-lubancat的rk3568教程,本篇记录了在正点原子的ATK-DLK3568部署。 一、介绍 ResNet18 是一种卷积神经网络,它有 18 层深度,其中包括带有权重的卷积层和全连接层。它…...

块状数据结构学习笔记
分块 分块的思想和珂朵莉树很类似,就是把原序列分成若干个块,对块进行操作的奇妙思想。复杂度通常带根号。分块的块长也有讲究,通常对于大小为 n n n 的数组,取距离 n \sqrt n n 最近的 2 2 2 的幂数或直接取 n \sqrt n n…...
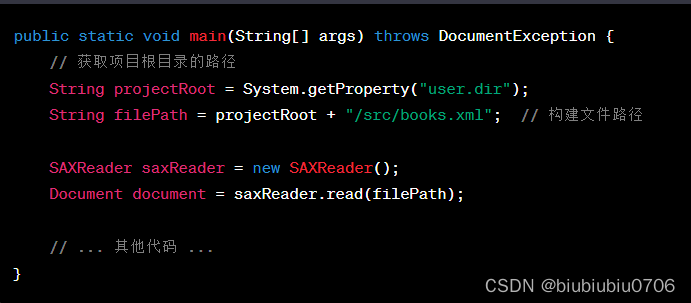
DOM4J解析.XML文件
<?xml version"1.0" encoding"utf-8" ?> <books><book id"SN123123413241"><name>java编程思想</name><author>华仔</author><price>9.9</price></book><book id"SN1234…...
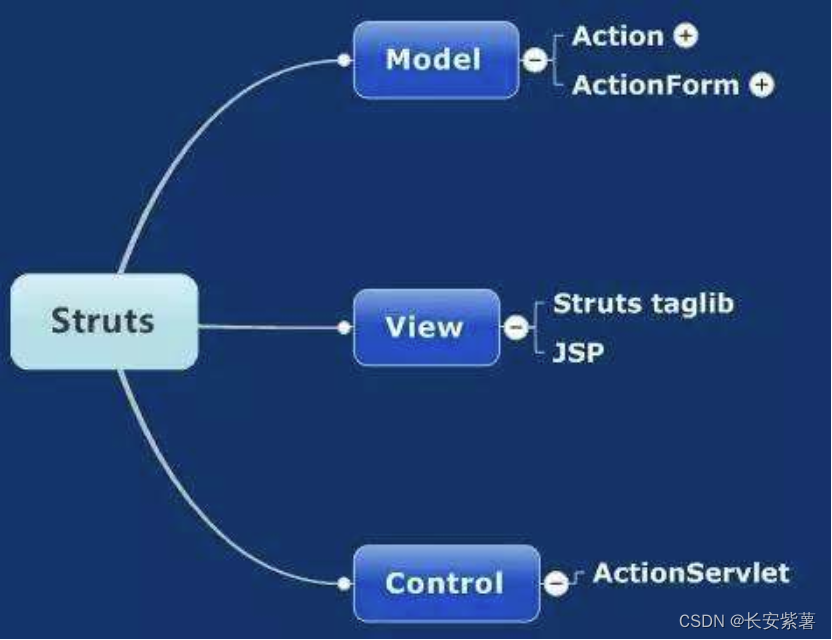
黑豹程序员-架构师学习路线图-百科:MVC的演变终点SpringMVC
MVC发展史 在我们开发小型项目时,我们代码是混杂在一起的,术语称为紧耦合。 如最终写ASP、PHP。里面既包括服务器端代码,数据库操作的代码,又包括前端页面代码、HTML展现的代码、CSS美化的代码、JS交互的代码。可以看到早期编程就…...
二、BurpSuite Intruder暴力破解
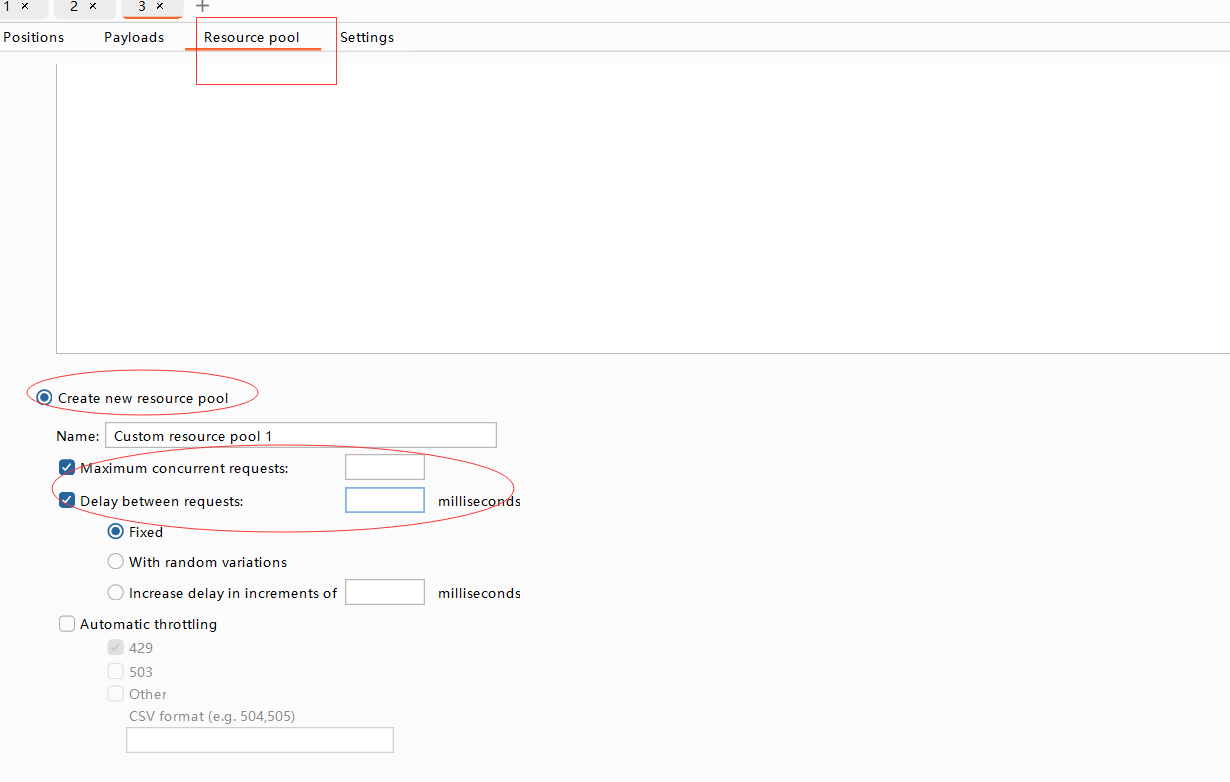
一、介绍 解释: Burp Suite Intruder是一款功能强大的网络安全测试工具,它用于执行暴力破解攻击。它是Burp Suite套件的一部分,具有高度可定制的功能,能够自动化和批量化执行各种攻击,如密码破解、参数枚举和身份验证…...
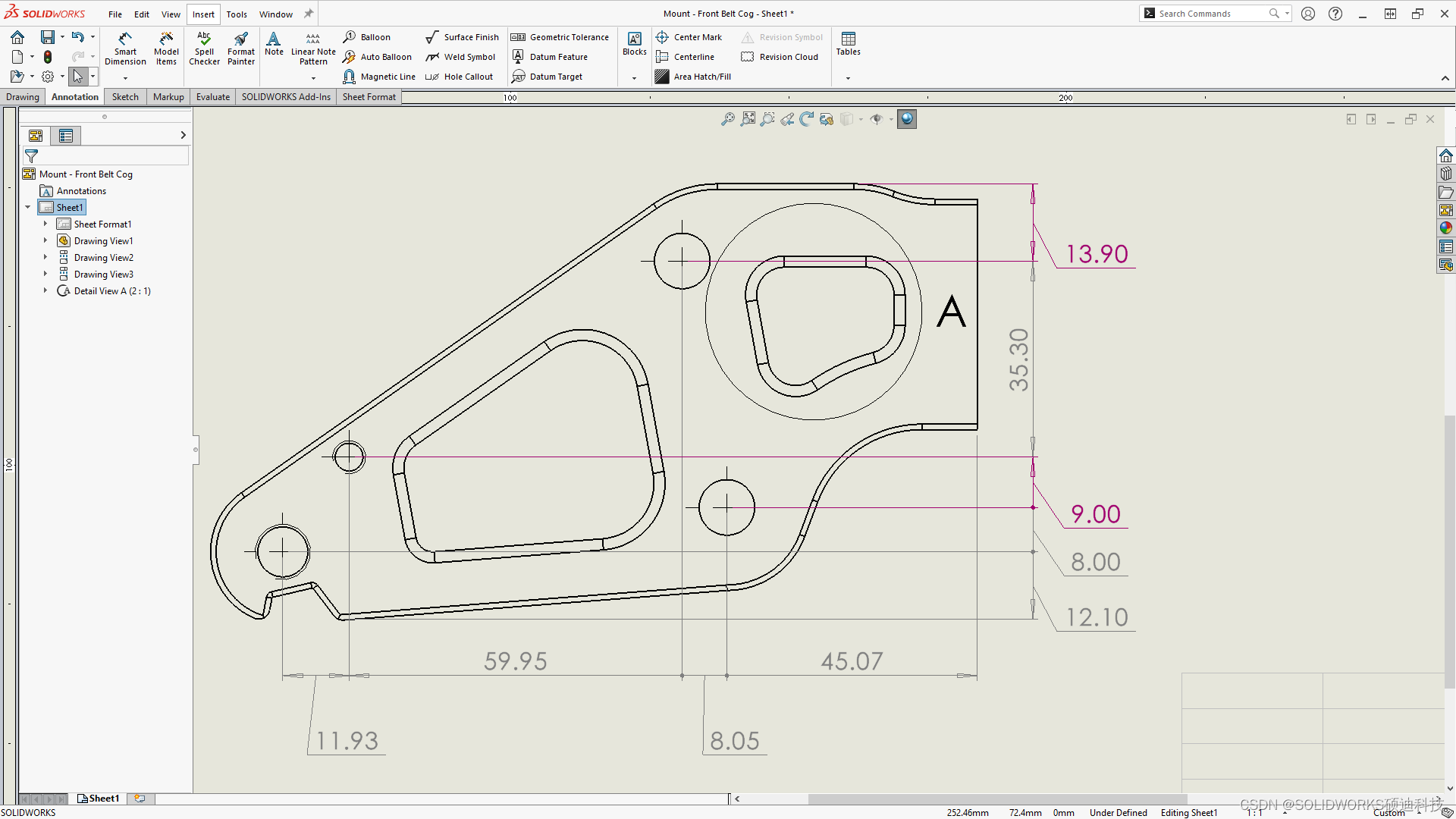
solidworks 2024新功能之-让您的工作更加高效
您可以创建杰出的设计,并将这些杰出的设计将融入产品体验中。为了帮您简化和加快由概念到成品的产品开发流程,SOLIDWORKS 2024 涵盖全新的用户驱动型增强功能,致力于帮您实现更智能、更快速地与您的团队和外部合作伙伴协同工作。 SOLIDWORKS…...
华为eNSP配置专题-VRRP的配置
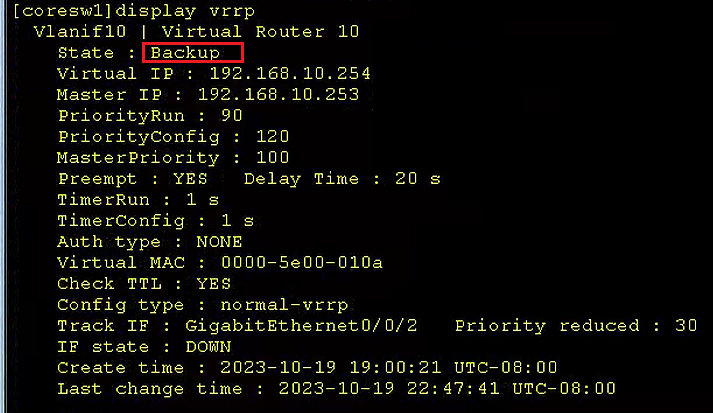
文章目录 华为eNSP配置专题-VRRP的配置0、参考文档1、前置环境1.1、宿主机1.2、eNSP模拟器 2、基本环境搭建2.1、基本终端构成和连接 2.VRRP的配置2.1、PC1的配置2.2、接入交换机acsw的配置2.3、核心交换机coresw1的配置2.4、核心交换机coresw2的配置2.5、配置VRRP2.6、配置出口…...
--lcd - lcd驱动模块)
LuatOS-SOC接口文档(air780E)--lcd - lcd驱动模块
常量 常量 类型 解释 lcd.font_opposansm8 font 8号字体 lcd.font_unifont_t_symbols font 符号字体 lcd.font_open_iconic_weather_6x_t font 天气字体 lcd.font_opposansm10 font 10号字体 lcd.font_opposansm12 font 12号字体 lcd.font_opposansm16 font…...
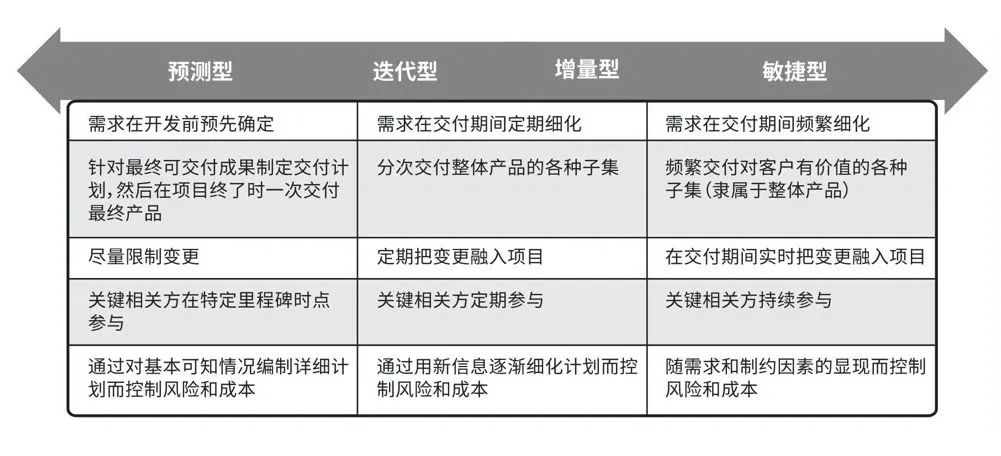
敏捷是怎么提高工作效率的
敏捷管理是一门极力减少不必要工作量的艺术。 谷歌、亚马逊、苹果、微信、京东等全球 500 强企业都在用的管理方法,适用于各行各业,被盛赞为应获“管理学的诺贝尔奖”。 它专注于让员工不受种种杂事的羁绊,激发个体斗志,释放出巨大…...

【C++】哈希的应用 -- 布隆过滤器
文章目录 一、布隆过滤器提出二、布隆过滤器概念三、布隆过滤器哈希函数个数的选择四、布隆过滤器的实现1.布隆过滤器的插入2.布隆过滤器的查找3.布隆过滤器删除4.完整代码实现 五、布隆过滤器总结1.布隆过滤器优点2.布隆过滤器缺陷3.布隆过滤器的应用4.布隆过滤器相关面试题 一…...

如何在Git中修改远程仓库地址
原文(可不登录复制代码):如何在Git中修改远程仓库地址-北的杂货间 Git是广泛使用的分布式版本控制系统,它允许开发者在本地仓库上工作,并将更改上传到远程仓库。然而,有时候你可能需要修改远程仓库的地址&…...
函数)
Go语言的sync.Once()函数
sync.Once 是 Go 语言标准库 sync 包提供的一个类型,它用于确保一个函数只会被执行一次,即使在多个 goroutine 中同时调用。 sync.Once 包含一个 Do 方法,其签名如下: func (o *Once) Do(f func()) Do 方法接受一个函数作为参数…...

修改 Stable Diffusion 使 api 接口增加模型参数
参考:https://zhuanlan.zhihu.com/p/644545784 1、修改 modules/api/models.py 中的 StableDiffusionTxt2ImgProcessingAPI 增加模型名称 StableDiffusionTxt2ImgProcessingAPI PydanticModelGenerator("StableDiffusionProcessingTxt2Img",StableDiff…...
微信小程序自定义组件及会议管理与个人中心界面搭建
一、自定义tabs组件 1.1 创建自定义组件 新建一个components文件夹 --> tabs文件夹 --> tabs文件 创建好之后win7 以上的系统会报个错误:提示代码分析错误,已经被其他模块引用,只需要在 在project.config.json文件里添加两行配置 &…...
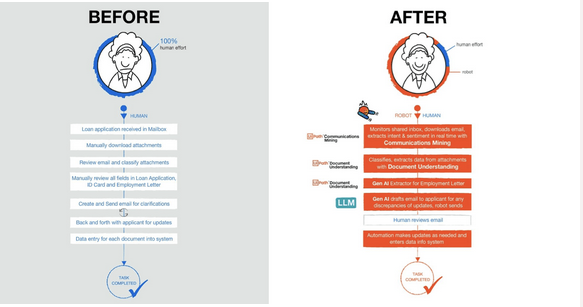
UiPath:一家由生成式AI驱动的流程自动化软件公司
来源:猛兽财经 作者:猛兽财经 总结: (1)UiPath(PATH)的股价并没有因为生成式AI的炒作而上涨,但很可能会成为主要受益者。 (2)即使在严峻的宏观环境下,UiPath的收入还在不…...

使用AI编写测试用例——详细教程
随着今年chatGPT的大热,每个行业都试图从这项新技术当中获得一些收益我之前也写过一篇测试领域在AI技术中的探索:软件测试中的AI——运用AI编写测试用例现阶段AI还不能完全替代人工测试用例编写,但是如果把AI当做一个提高效率的工具ÿ…...
又哭又笑,这份面试宝典要是早遇到就好了
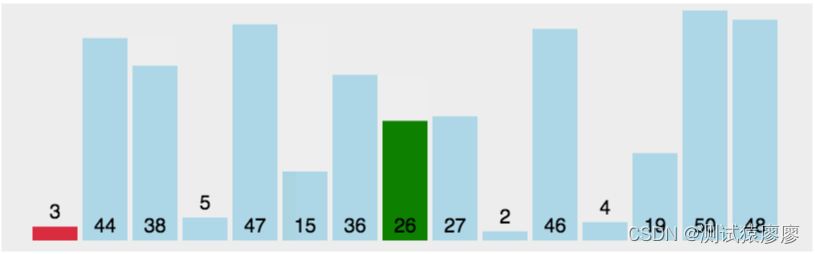
01、算法原理 选择排序(Selection sort)是一种简单直观的排序算法。 第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素&#…...
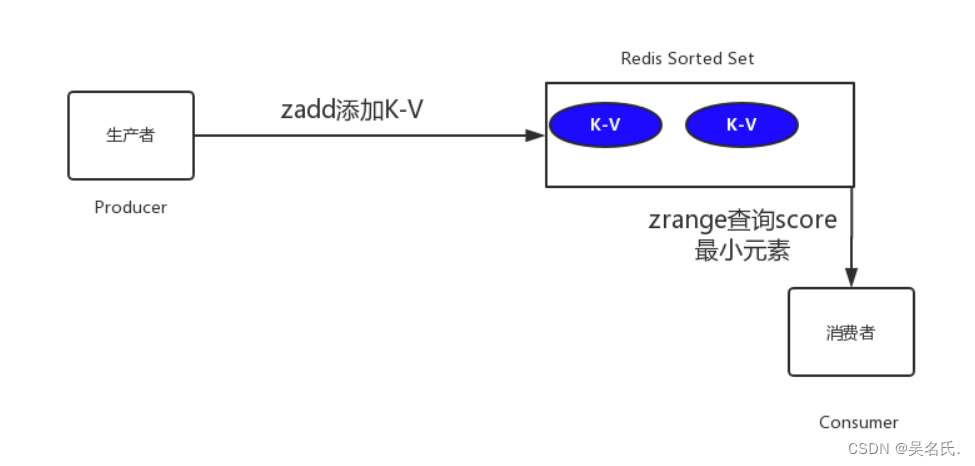
订单30分钟自动关闭的五种解决方案
1 前言 在开发中,往往会遇到一些关于延时任务的需求。例如 生成订单30分钟未支付,则自动取消生成订单60秒后,给用户发短信 对上述的任务,我们给一个专业的名字来形容,那就是延时任务 。那么这里就会产生一个问题,这…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
