力扣每日一题59:螺旋矩阵||
题目描述:
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:

输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 20
通过次数
361.6K
提交次数
503.1K
通过率
71.9%
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:

输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 20
通过次数
361.6K
提交次数
503.1K
通过率
71.9%
思路和题解:
与第54题一样的方法,也是从最外层到最里层的方法,第54题是矩阵生成序列,这个是序列生成矩阵。螺旋矩阵
代码:
class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> ans(n,vector<int>(n,0));int up=0,down=n-1,right=n-1,left=0;int num=1;while(true){for(int i=left;i<=right;i++){ans[up][i]=num;num++;}if(++up>down) break;for(int i=up;i<=down;i++){ans[i][right]=num;num++;}if(--right<left) break;for(int i=right;i>=left;i--){ans[down][i]=num;num++;}if(--down<up) break;for(int i=down;i>=up;i--){ans[i][left]=num;num++;}if(++left>right) break;}return ans;}
};相关文章:

力扣每日一题59:螺旋矩阵||
题目描述: 给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。 示例 1: 输入:n 3 输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2: 输入&am…...
codeforces (C++ In Love )
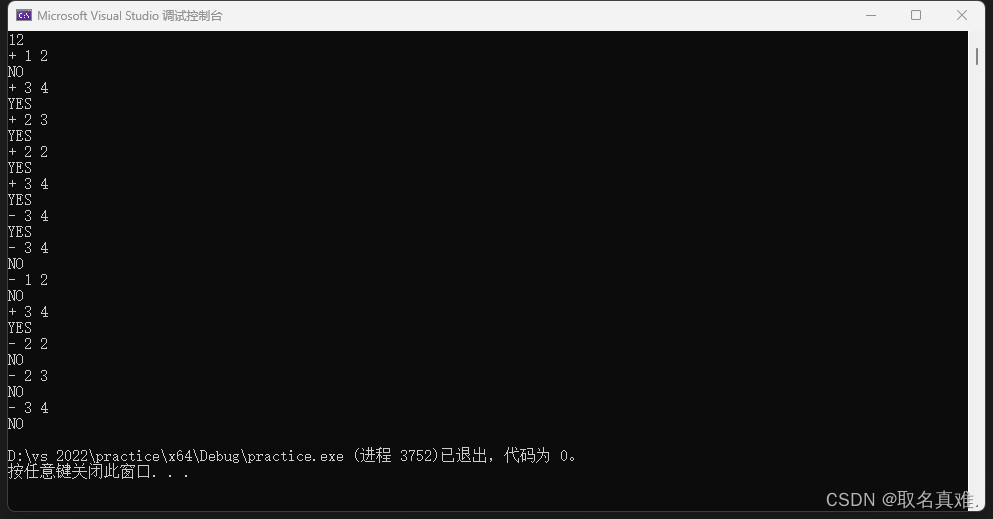
题目: 翻译: 思路: 1、在一个集合中有多组线段,如果有不相交的两组线段,则输出YES,否则输出NO。 2、每次操纵可以选择增加一组线段或者删除一组线段后,输出YES或者NO。 3、用flag标记该线段是否…...

【python】py文件全自动打包成spec文件
说明: 自动获取当前根目录下所有py文件生成spec文件,直接运行pyinstaller进行打包即可。直接打包成单执行文件。 直接上代码 import ospathex []def recursion(path, main):if path[:1] ! /:path /listpath os.listdir(path)for item in listpath:if…...
YOLOv5-调用官方权重进行检验(目标检测)
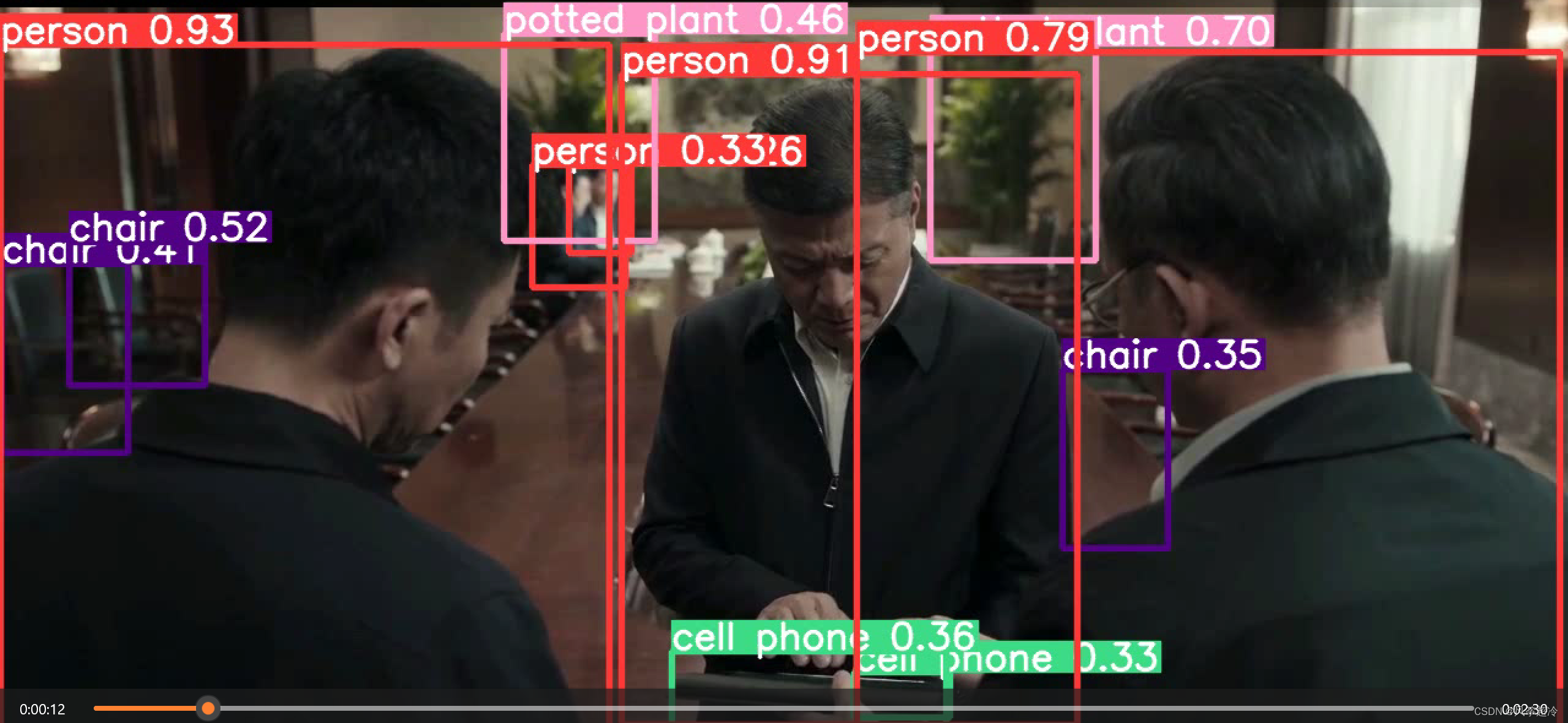
🍨 本文为[🔗365天深度学习训练营学习记录博客 🍦 参考文章:365天深度学习训练营-第7周:咖啡豆识别(训练营内部成员可读) 🍖 原作者:[K同学啊 | 接辅导、项目定制](https…...

springMVC中统一异常处理@ControllerAdvice
1.在DispatcherServlet中初始化HandlerExceptionResolver 2.controller执行完成后执行processDispatchResult(processedRequest,response,mappedHandler,mv,dispatchException),有异常则处理异常 3.ExcepitonHandlerExceptionResolver中执行方法doResolveHandlerMethodExceptio…...

【Java】<泛型>,在编译阶段约束操作的数据结构,并进行检查。
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ JAVA泛型 泛型介绍: ①泛型&#…...

解决谷歌学术bib信息不全的问题
在我们撰写学术论文时,经常需要引用参考文献。如果用latex撰写论文,势必会用到文献的bib信息,大部分的教程都会告诉我们去google scholar上去搜索。 一、问题描述 搜索一篇文章,然后选择cite,再选择bib。 很明显&…...

初始Redis 分布式结构的发展演变
目录 Redis的特点和使用场景 分布式系统的引入 单机系统 分布式系统 应用服务器的增多(处理更多的请求) 数据库读写分离(数据服务器的增多) 引入缓存 应对更大的数据量 业务拆分:微服务 Redis的特点和使用场景 我们先来…...

关于动态内存管理中的常见练习题
文章目录 前言练习1:练习2:练习3:练习4: 前言 学习完C语言中的动态内存管理,大家开始利用动态内存管理来去开辟空间,经过一顿狂敲代码后,发现了问题,程序要么崩掉,要么运…...

冒泡排序、插入排序、选择排序和快速排序的原理
下面是对冒泡排序、插入排序、选择排序和快速排序的原理的简要解释: 冒泡排序(Bubble Sort):冒泡排序是一种简单的排序算法。它通过多次迭代比较相邻的元素,并交换它们的位置,使得较大(或较小&…...

VB.NET之SqlCommand详解
目录 一.前言 二.SqlCommand的背景方法 1.构造函数 2.属性 3.方法 三.SqlCommand的使用实例 1.创建SqlCommand对象 2.执行SQL查询语句 3.执行存储过程 四.总结 一.前言 VB.NET的SqlCommand是ADO.NET的一部分,主要用于执行SQL语句并返回受影响的行数、查询…...

.NET主流的ORM框架 2023年
1. Entity Framework Entity Framework是Microsoft开发的一款强大的ORM框架。适用于.NET开发,支持多种数据库,并提供了广泛的文档和教程。Entity Framework基于面向对象的数据模型,使用LINQ进行查询。它的强大功能和易用性使得它成为.NET开发…...

第三节——Vue 基础语法
vue语法分为选项是API(Option api)和组合式api(Composition Api),我们以选项式Api入门 一、基本构成 template、script、style三部分构成。template可以理解成编写html的地方,script编写逻辑js的地方,sty…...
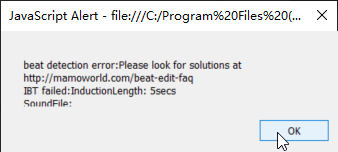
PR BeatEdit 节奏卡点神器 的报错 beat detection error: IBT failed 和解决路径
环境:DELL Latitude 笔记本 16G内衬,Win10,PR 2021,BeatEdit Pr 2.1.003 安装PR BeatEdit 节奏卡点神器没有问题,可以调出。 导入音频时报错:beat detection error: IBT failed 根据 BeatEdit for Premi…...

LeetCode75——Day13
文章目录 一、题目二、题解 一、题目 1679. Max Number of K-Sum Pairs You are given an integer array nums and an integer k. In one operation, you can pick two numbers from the array whose sum equals k and remove them from the array. Return the maximum num…...
)
【单元测试】--测试驱动开发(TDD)
一、什么是测试驱动开发 测试驱动开发(Test-Driven Development,TDD)是一种软件开发方法,其核心思想是在编写实际代码之前,首先编写测试用例。TDD 的主要步骤如下: 编写测试用例:首先…...

【计算机网络】UDP的报文结构和注意事项
UDP(User Datagram Protocol,用户数据报协议)是一种无连接的协议,它在传输层中提供了简单、不可靠的数据传输服务。与TCP(Transmission Control Protocol,传输控制协议)不同,UDP不需要建立连接&…...
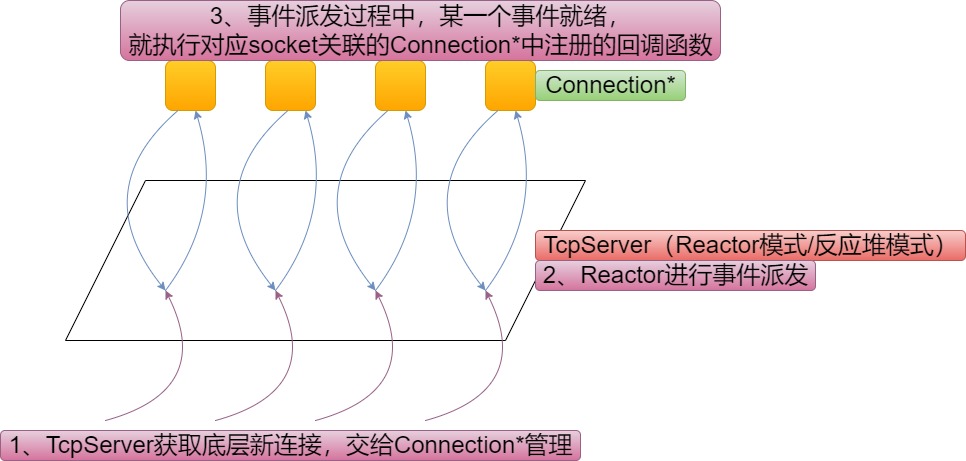
【网络编程】基于epoll的ET模式下的Reactor
需要云服务器等云产品来学习Linux的同学可以移步/-->腾讯云<--/-->阿里云<--/-->华为云<--/官网,轻量型云服务器低至112元/年,新用户首次下单享超低折扣。 目录 一、Reactor介绍 二、基于epoll的ET模式下的Reactor计算器代码 1、Tcp…...

位操作符^以及正负数在计算机中的存储
(数据是怎么在计算机中存储的) 正数和负数在内存中都是以补码的形式存储的,但不同的是正数的原码,补码,反码都是相同的,而负数的原码,补码和反码是不同的。 负数的原码,补码,反码之间存在什么…...
Linux系统管理:虚拟机Kylin OS安装
目录 一、理论 1.Kylin OS 二、实验 1.虚拟机Kylin OS安装准备阶段 2.安装Kylin OS 3.进入系统 一、理论 1.Kylin OS (1)简介 麒麟操作系统(Kylin OS)亦称银河麒麟,是由中国国防科技大学、中软公司、联想公司…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
