大厂秋招真题【贪心】美团20230826秋招T2-小美的数组重排
文章目录
- 【贪心】美团2023秋招-小美的数组重排
- 题目描述与示例
- 题目描述
- 输入描述
- 输出描述
- 示例
- 输入
- 输出
- 说明
- 解题思路
- 代码
- Python
- Java
- C++
- 时空复杂度
- 华为OD算法/大厂面试高频题算法练习冲刺训练
【贪心】美团2023秋招-小美的数组重排
题目描述与示例
题目描述
小美有两个长度为n的数组a和b。
小美想知道,能不能通过重排a数组使得对于任意1 <= i <= n, 1 <= ai+bi <= m?
将会有q次询问。
输入描述
第一行一个整数q (1 <= q <= 30)。表示询问次数。
对于每一个询问:
第一行输入两个整数n, m (1 <= n, m <= 500)
第二行输入n个整数ai (-500 <= ai <= 500)
第三行输入n个整数bi (-500 <= bi <= 500)
输出描述
q行,每行输出一个字符串,如果能通过重排满足条件则输出"Yes"(不含引号),否则输出"No"。
示例
输入
2
5 3
-1 -2 3 4 5
-1 3 4 2 5
5 6
-1 -2 3 4 5
-1 3 4 2 5
输出
No
Yes
说明
对于第一个用例,无论怎么重排都不满足条件。
对于第二个用例,将数组a重排为[5,3,-2,4,-1]时满足条件。
解题思路
注意,本题和LeetCode881. 救生艇 的思路非常相似。
贪心地思考问题,首先选择a数组中的最小值和b数组中的最大值相加,若结果不满足1 <= ai+bi <= m,如
ai+bi > m,则说明b数组中的最大值太大,a数组中选择其他值与b中的最大值相加更不可能满足条件ai+bi < 1,则说明a数组中的最小值太大,b数组中选择其他值与a中的最小值相加更不可能满足条件
若上述结果满足1 <= ai+bi <= m,则同样地考虑a中的次小值,b中的次大值,依次类推。
故我们只需要对a数组和b数组分别进行升序和降序排序,考虑同一位置的两个元素相加是否满足1 <= ai+bi <= m即可。
代码
Python
# 题目:【贪心】美团2023秋招-小美的数组重排
# 作者:闭着眼睛学数理化
# 算法:贪心/排序
# 代码有看不懂的地方请直接在群上提问# 对于每组询问,求解的函数
def solve(n, m, a, b):# 对a升序排序,对b逆序排序a.sort()b.sort(reverse = True)# 遍历a和b中同一位置的元素for i in range(n):# 若同一个位置的元素相加大于m,# 则无法满足重排要求,返回"No"if a[i] + b[i] > m or a[i] + b[i] < 1:return "No"# 若成功退出循环,则返回"Yes"return "Yes"# 询问次数q
q = int(input())
ans = list()for _ in range(q):# 对于每一次询问,输入三行# 分别为数组长度n,整数m,数组a和bn, m = map(int, input().split())a = list(map(int, input().split()))b = list(map(int, input().split()))ans.append(solve(n, m, a, b))for s in ans:print(s)
Java
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int q = scanner.nextInt();List<String> ans = new ArrayList<>();for (int t = 0; t < q; t++) {int n = scanner.nextInt();int m = scanner.nextInt();int[] a = new int[n];for (int i = 0; i < n; i++) {a[i] = scanner.nextInt();}int[] b = new int[n];for (int i = 0; i < n; i++) {b[i] = scanner.nextInt();}ans.add(solve(n, m, a, b));}for (String s : ans) {System.out.println(s);}}private static String solve(int n, int m, int[] a, int[] b) {List<Integer> aList = new ArrayList<>();List<Integer> bList = new ArrayList<>();for (int num : a) {aList.add(num);}for (int num : b) {bList.add(num);}Collections.sort(aList);Collections.sort(bList, Collections.reverseOrder());for (int i = 0; i < n; i++) {if (aList.get(i) + bList.get(i) > m || aList.get(i) + bList.get(i) < 1) {return "No";}}return "Yes";}
}
C++
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;string solve(int n, int m, vector<int>& a, vector<int>& b) {sort(a.begin(), a.end());sort(b.begin(), b.end(), greater<int>());for (int i = 0; i < n; i++) {if (a[i] + b[i] > m || a[i] + b[i] < 1) {return "No";}}return "Yes";
}int main() {int q;cin >> q;vector<string> ans;for (int t = 0; t < q; t++) {int n, m;cin >> n >> m;vector<int> a(n);for (int i = 0; i < n; i++) {cin >> a[i];}vector<int> b(n);for (int i = 0; i < n; i++) {cin >> b[i];}ans.push_back(solve(n, m, a, b));}for (const string& s : ans) {cout << s << endl;}return 0;
}
时空复杂度
时间复杂度:O(NlogN)。排序所需的时间复杂度。
空间复杂度:O(1)。不考虑排序所需要的空间,只需要若干常数变量。
华为OD算法/大厂面试高频题算法练习冲刺训练
-
华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名!目前已服务100+同学成功上岸!
-
课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化
-
每期人数维持在20人内,保证能够最大限度地满足到每一个同学的需求,达到和1v1同样的学习效果!
-
60+天陪伴式学习,40+直播课时,300+动画图解视频,300+LeetCode经典题,200+华为OD真题/大厂真题,还有简历修改、模拟面试、专属HR对接将为你解锁
-
可上全网独家的欧弟OJ系统练习华子OD、大厂真题
-
可查看链接 大厂真题汇总 & OD真题汇总(持续更新)
-
绿色聊天软件戳
od1336了解更多
相关文章:

大厂秋招真题【贪心】美团20230826秋招T2-小美的数组重排
文章目录 【贪心】美团2023秋招-小美的数组重排题目描述与示例题目描述输入描述输出描述示例输入输出 说明 解题思路代码PythonJavaC时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 【贪心】美团2023秋招-小美的数组重排 题目描述与示例 题目描述 小美有两个长度为n…...

UnitTest框架的使用
文章目录 一、UnitTest框架是什么?二、UnitTest核心要素三、TestCase四、TestSuite & TestRunner 一、UnitTest框架是什么? UnitTest框架是python自带的一个单元测试框架,主要用它来做单元测试,它有以下特点: 能…...

软件开发项目文档系列之四如何成功撰写一份引人注目的投标文件
目录 前言1 分析招标文件1.1 投标的基础要求分析1.2 投标重点要求分析1.3 评分标准分析1.4 技术需求分析 2 撰写完整的投标文件2.1 明确文件用途2.2 提供评分指引2.3 内容完整重点突出2.4 重视图表和图示 3 认真检查和经验积累3.1 深入的准备3.2 反复检查3.3 咨询和确认3.4 积累…...

Django设置跨域
1, 安装 pip install django-cors-headers 2, 添加应用 INSTALLED_APPS (...corsheaders,... ) 3, 中间层设置 MIDDLEWARE [corsheaders.middleware.CorsMiddleware,... ] 4, 添加白名单 # CORS CORS_ORIGIN_WHITELIST (127.0.0.1:8080,localhost:8080,www.meiduo.si…...
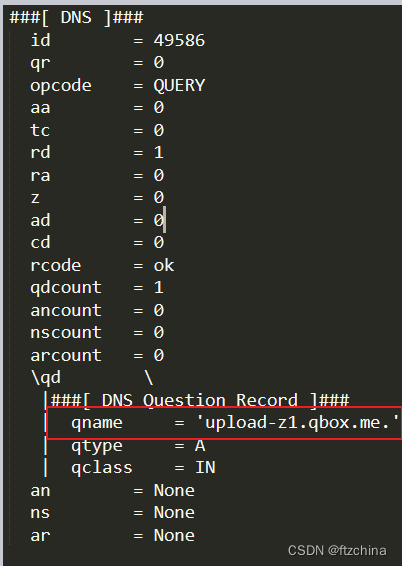
基于Python3的Scapy构造DNS报文
一:DNS协议 DNS(Domain Name System)协议是计算机网络中的一种基础协议,它用于将域名(如www.baidu.com)转换为IP地址(如192.168.0.1),从而实现计算机之间的通信。 DNS 分…...

Jupyter Notebook修改默认浏览器方法
Jupyter Notebook修改默认浏览器方法 Create a Jupyter Notebook Config file jupyter notebook --generate-config打开配置文件.jupyter/jupyter_notebook_config.py找到c.NotebookApp.browser 改成只向自己喜欢的浏览器路径’,这里给出选择google浏览器方法&…...

云计算系统与传统计算系统的比较
随着技术的不断发展,云计算系统逐渐成为了企业和个人使用的主要计算方式之一。然而,很多人对云计算系统与传统计算系统之间的区别和相似之处还存在一些疑惑。本文将以云计算系统和传统计算系统为方向,探讨它们之间的异同点。 首先࿰…...
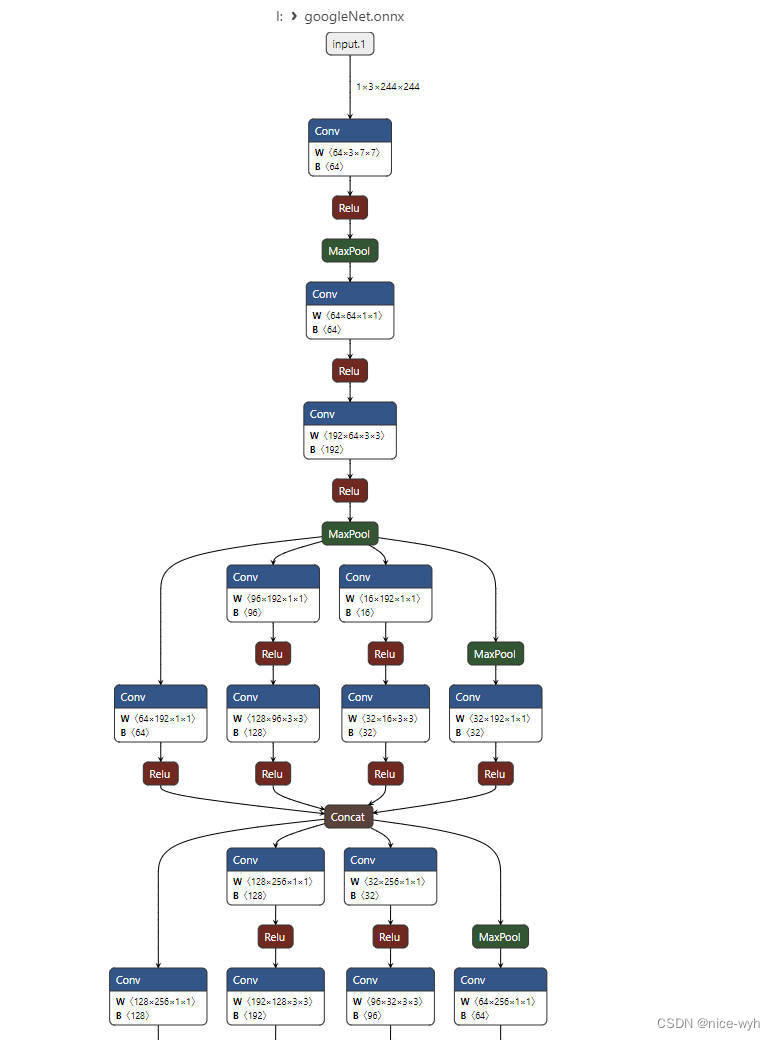
使用GoogleNet网络实现花朵分类
一.数据集准备 新建一个项目文件夹GoogleNet,并在里面建立data_set文件夹用来保存数据集,在data_set文件夹下创建新文件夹"flower_data",点击链接下载花分类数据集https://storage.googleapis.com/download.tensorflow.org/exampl…...

STM32之Bootloader、USB、IAP/DFU下载
STM32 IAP应用开发——通过内置DFU实现USB升级(方式2) STM32 IAP应用开发——通过内置DFU实现USB升级(方式1) STM32程序下载4:通过STM32CubePro-USB下载 STM32程序下载3:通过STM32CubePro-UART下载 STM…...

解决 Element-ui中 表格(Table)使用 v-if 条件控制列显隐时数据展示错乱的问题
本文 Element-ui 版本 2.x 问题 在 el-table-column 上需根据不同 v-if 条件来控制列显隐时,就会出现列数据展示错乱的情况(要么 A 列的数据显示在 B 列上,或者后端返回有数据的但是显示的为空),如下所示。 <tem…...

Android JNI笔记
JNI、java native interface 。可以实现Java和C、C之间的调用。 在Android开发中是必须要掌握的内容。 在应用开发中,编写JNI代码的注册可分为动态注册和静态注册 动态注册: 声明好方法、注意这些签名 在JNI_OnLoad中进行注册。 static const JNINativ…...
方法)
Web开发中会话跟踪的隐藏表单字段(隐藏input)方法
隐藏表单字段是一种会话跟踪方法,通过在HTML表单中添加一个隐藏字段来存储会话标识符。 这样,每次用户提交表单时,会话标识符将与请求一起发送到服务器,以便服务器可以跟踪用户的会话状态。 以下是一个隐藏表单字段的示例&#…...

线性代数相关笔记
线性基 导入 线性基,顾名思义,就是一个包含数字最少的集合,使得原集合中的任何数都能用线性基中的元素表示。 集合中的元素满足一些性质: 原集合中的任意元素都可以用线性基中的若干元素的异或和表示线性基中任意数异或和不为…...
】69 - Android 侧添加支持 busybox telnetd 服务)
【SA8295P 源码分析 (四)】69 - Android 侧添加支持 busybox telnetd 服务
【SA8295P 源码分析】69 - Android 侧添加支持 busybox telnetd 服务 一、下载 busybox-1.36.1.tar.bz2 源码包二、编译 busybox 源码三、将编译后的 busybox 打包编入Android 镜像中系列文章汇总见:《【SA8295P 源码分析 (四)】网络模块 文章链接汇总 - 持续更新中》 本文链接…...
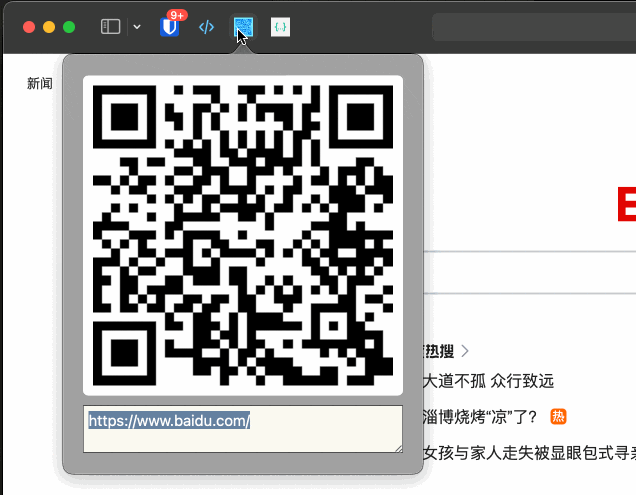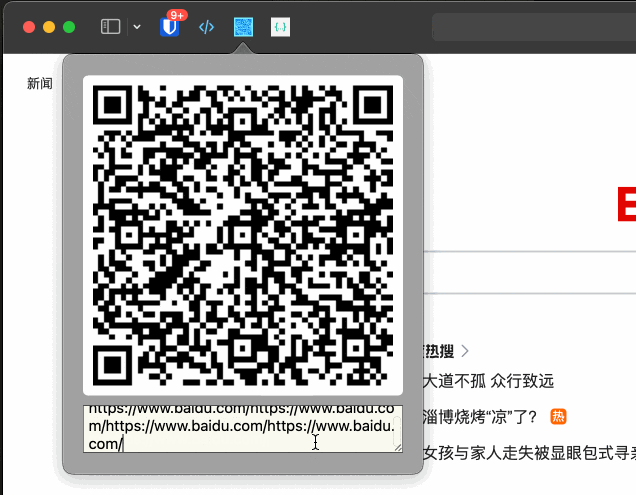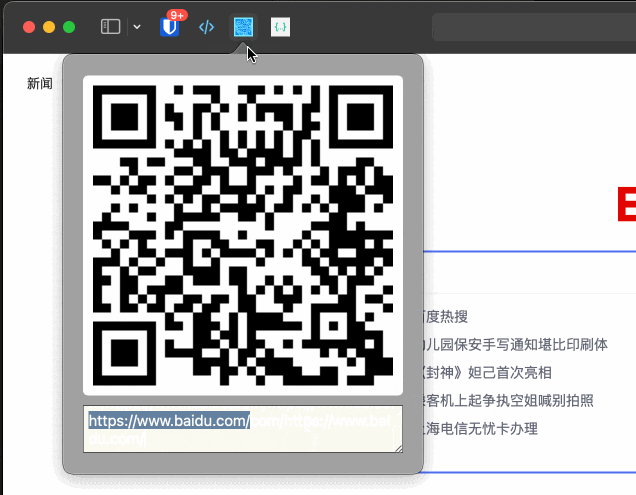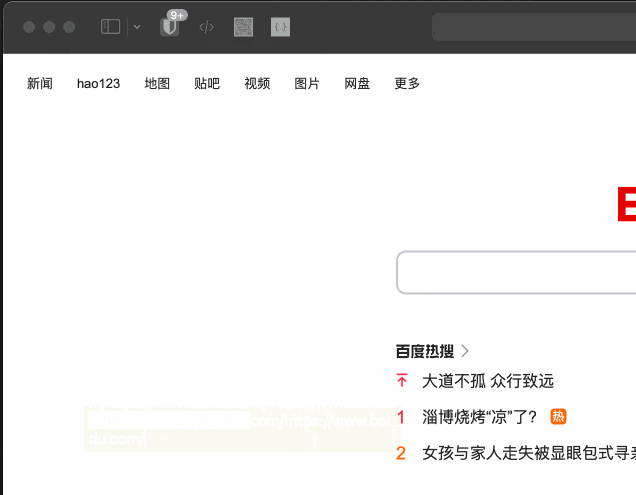
如何开发一个 Safari 插件
本文字数:2493字 预计阅读时间:15分钟 由于常用浏览器是Safari,而Safari浏览器的插件比不上Chrome,所以就有了自己开发常用的Safari插件的想法。 打算开发当前页面生成二维码的Extension,因为网络原因,AirD…...

n皇后问题,不用递归
注释如下: class Solution:def totalNQueens(self, n: int) -> int:if n < 1: # 如果 n 小于 1,直接返回 0return 0count 0 # 初始化解的个数为 0stack [(0, set(), set(), set())] # 初始化一个栈,元素为当前处理的行数、已经放…...
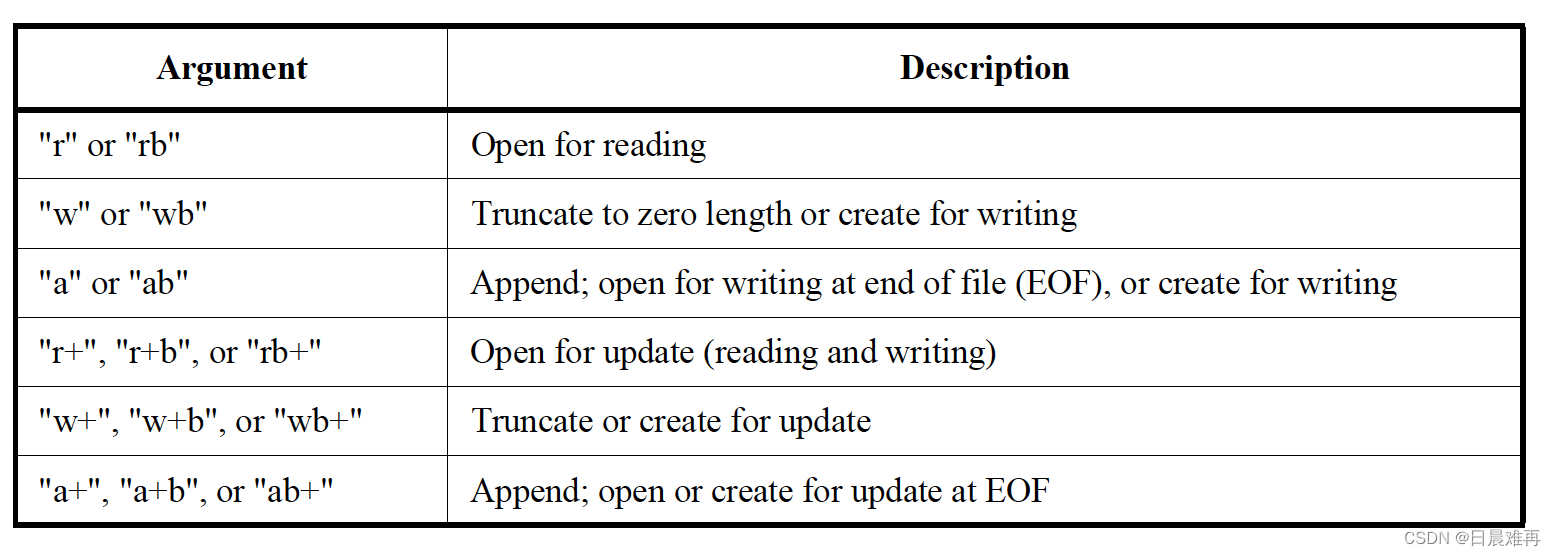
Verilog基础:$fopen和$fclose系统函数、任务的使用
相关阅读 Verilog基础https://blog.csdn.net/weixin_45791458/category_12263729.html?spm1001.2014.3001.5482 $fopen和$fclose是两个用于打开和关闭文件的系统函数、任务。最初,在Verilog-1995标准中,最多只能同时打开32个文件,其所使用的…...

python之字典的用法
python之字典的用法 Python中的字典是一种无序、可变、可迭代的数据类型,它由键值对组成,每个键都映射到一个值。字典在Python中被视为可变对象,这意味着我们可以随时更新、添加或删除字典中的键值对。 以下是一些关于Python字典的基本用法&a…...
Leetcode1971. 寻找图中是否存在路径
Every day a Leetcode 题目来源:1971. 寻找图中是否存在路径 解法1:并查集 并查集介绍:并查集详解 代码: /** lc appleetcode.cn id1971 langcpp** [1971] 寻找图中是否存在路径*/// lc codestart class UnionFind {vector&…...

程序可以创建多少个用户界面对象?
有人提到这样一个问题:”一个程序最多可以注册多少个窗口类?” 问题的答案不是一个具体的数字。因为大多数用户界面对象都来自一个共享的内存池,我们称之为”桌面堆内存”。尽管我们可以计算一个最大的理论值,但是在实际的场景中࿰…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
