ZKP6.1 Discrete-log-based Polynomial Commitments (Preliminary)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 6: Discrete-log-based Polynomial Commitments (Yupeng Zhang)
- Recall
- How to build an efficient SNARK?
- A polynomial commitment scheme + A polynomial interactive oracle proof (IOP) = SNARK for general circuits
- Plonk
- Univariate polynomial commitment + Plonk Polynomial IOP = SNARK for general circuits
- Interactive proofs
- Multivariate polynomial commitment + Sumcheck protocol = SNARK for general circuits
- polynomial commitment

- How to build an efficient SNARK?

6.1 Background
- Group: Closure, Associativity, Identity, Inverse.
- Generator of a group: An element g g g that generates all elements in the group by taking all powers of g g g
- Discrete logarithm assumption
- A group G G G has an alternative representation as the powers of the generator g g g: { g , g 2 , g 3 , . . . , g p − 1 } \{g, g^2, g^3,...,g^{p-1}\} {g,g2,g3,...,gp−1}
- Discrete logarithm problem: given y ∈ G y \in G y∈G, find x x x s.t. g x = y g^x = y gx=y
- Discrete-log assumption: discrete-log problem is computationally hard.
- (Computational) Diffie-Hellman assumption: Given G , g , g x , g y G, g, g^x, g^y G,g,gx,gy, cannot compute g x y g^{xy} gxy
- Bilinear pairing:
- ( p , G , g , G T , e ) (p, G, g, G_T, e) (p,G,g,GT,e)
- G G G and G T G_T GT are both multiplicative cyclic groups of order p p p, g g g is the generator of G G G.
- G G G: base group, G T G_T GT target group
- Pairing: e ( P x , Q y ) = e ( P , Q ) x y e(P^x,Q^y) = e(P,Q)^{xy} e(Px,Qy)=e(P,Q)xy
- Example: e ( g x , g y ) = e ( g , g ) x y = e ( g x y , g ) e(g^x,g^y) = e(g,g)^{xy} = e(g^{xy},g) e(gx,gy)=e(g,g)xy=e(gxy,g)
- Given g x g^x gx and g y g^y gy , a pairing can check that some element h = g x y h = g^{xy} h=gxy without knowing x x x and y y y.
- BLS signature [Boneh–Lynn–Shacham’2001]

相关文章:

ZKP6.1 Discrete-log-based Polynomial Commitments (Preliminary)
ZKP学习笔记 ZK-Learning MOOC课程笔记 Lecture 6: Discrete-log-based Polynomial Commitments (Yupeng Zhang) Recall How to build an efficient SNARK? A polynomial commitment scheme A polynomial interactive oracle proof (IOP) SNARK for general circuits Plo…...
五金经营小程序商城的作用体现在哪
对消费者而言,如今线上购买五金是很多人的选择,传统线下购买,不仅需要跑路,而且店内未必有所需品,但线上平台则一目了然购买所需品,本地/外地均可以触达到,同时还可对用户/会员进行高效管理&…...

今年这行情,不会自动化的要做好心理准备了
李强是一名软件测试工程师,入行之后在一家小型公司工作了五年。这段时间里,他主要负责手工测试和一些简单的自动化测试工作。由于公司项目也相对简单,他逐渐陷入了工作的舒适区,没有积极追求新的知识和技能。 然而随着身边朋友发展…...

汽车保养笔记
汽车保养笔记 汽车小保养汽车大保养五油:机油变速箱油刹车油转向助力油离合器油 四滤:机油滤芯更换空气滤芯更换空调滤芯更换汽油滤芯更换 三水防冻液(水)玻璃水电瓶水 其他刹车片球头减震器火花塞 4S店的4大套路---没必要清洗节气门更换火花塞和高压线圈…...

【斗破年番】官方改编用心了,彩鳞怀孕并未删,萧潇肯定登场,真相在丹药身上
【侵权联系删除】 【文/郑尔巴金】 斗破苍穹年番动画已经更新了,相信不少人都感觉到不可思议,萧炎跟随美杜莎女王回蛇人族的剧情,居然魔改成这样。好好的腹中孕育出新生命,变成了陨落心炎残余能量,不及时处理的话&…...

英语——分享篇——每日200词——3201-3400
3201——air-conditioning——[eərkəndɪʃnɪŋ]——n.空调设备;vt.给…装上空调——air-conditioning——air-condition空调(熟词)ing鹰(谐音)——空调设备的噪音让鹰不得安宁——The trains dont even have proper air-conditioning, grumbles Mr So. ——地铁…...
)
合并区间(C++解法)
题目 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 1: 输入:intervals …...
CUDA学习笔记(十四) Constant Memory
转载至https://www.cnblogs.com/1024incn/tag/CUDA/ CONSTANT MEMORY constant Memory对于device来说只读但是对于host是可读可写。constant Memory和global Memory一样都位于DRAM,并且有一个独立的on-chip cache,比直接从constant Memory读取要快得多…...
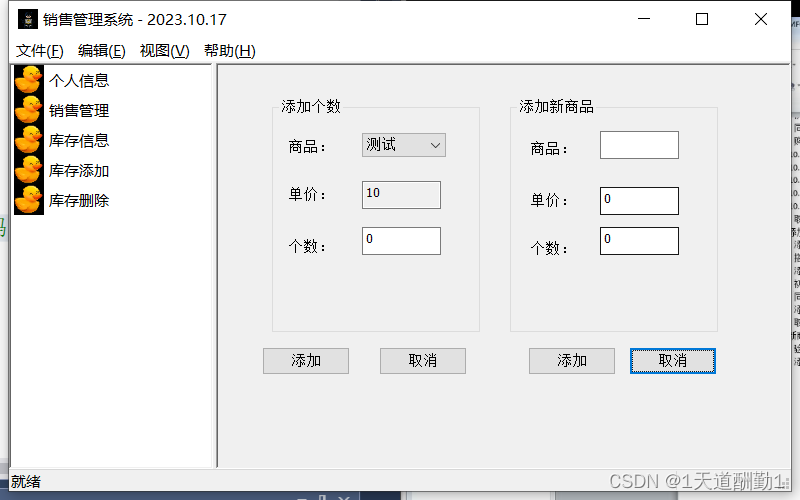
使用MFC创建一个SaleSystem
目录 1、项目的创建: 2、项目的配置: 3、设置窗口属性: (1)、设置图标 1)、添加导入资源 2)、代码初始化图标 (2)、设置标题 (3)、设置窗口…...
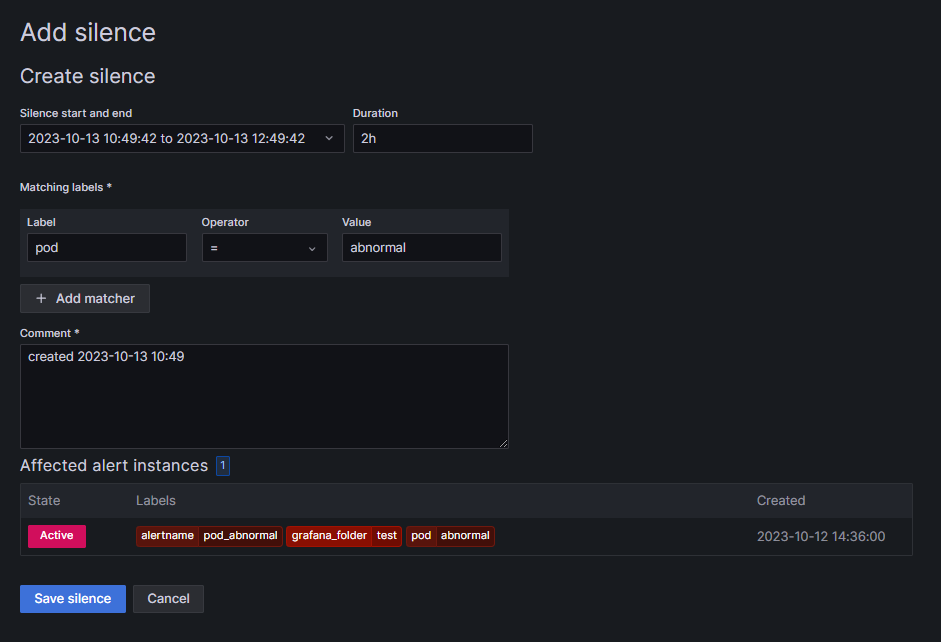
grafana v10.1版本设置告警
1. 相关概念概述 如图所示,点击切换菜单标志,可以看到警报相关子选项。 警报规则:通过PromQL语句定义告警规则,即达到怎样的状态触发告警。 联络点: 设置当警报规则实例触发时,如何通知联系人,…...

Python+Requests+PyTest+Excel+Allure 接口自动化测试实战
本文主要介绍了PythonRequestsPyTestExcelAllure 接口自动化测试实战,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧 Unittest是Python标准库中自带的单元测试框架…...
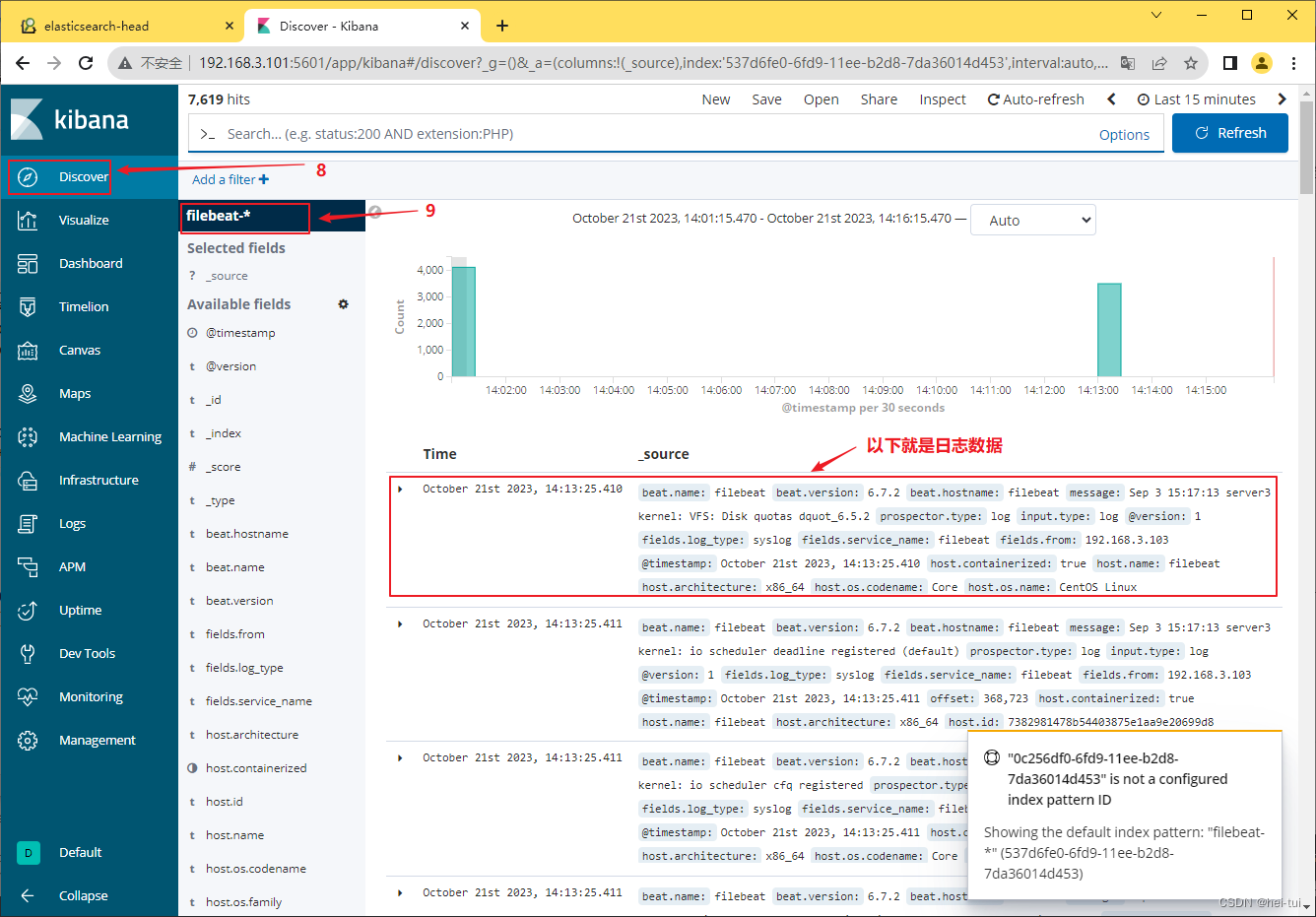
日志分析系统——ELK
目录 一、ELK概述 ELK的组成 1、ElasticSearch 2、Logstash 3、Kiabana 完整日志采集系统基本特征 ELK的工作原理 二、ELK的部署 1、环境准备 2、部署ElasticSearch软件 3、安装Elasticsearch-head插件 4、Logstash部署 5、Kibana部署 三、FilebeatELK部署 1、安…...
Ubuntu小知识总结
Ubuntu相关的小知识总结 一、Ubuntu系统下修改用户开机密码二、Vmware虚拟机和主机之间复制、粘贴内容、拖拽文件的详细方法问题描述Vmware tools灰色不能安装解决方法小知识点:MarkDown的空格 三、Ubuntu虚拟机网络无法连接的几种解决方法1.重启网络编辑器2. 重启虚…...

2023年全球市场新能源汽车车载充电器总体规模、主要生产商、主要地区、产品和应用细分研究报告
按收入计,2022年全球新能源汽车车载充电器收入大约 百万美元,预计2029年达到 百万美元,2023至2029期间,年复合增长率CAGR为 %。同时2022年全球新能源汽车车载充电器销量大约 ,预计2029年将达到 。2022年中国市场规模大…...

基于stm32控制的ESP8266在设备模式下通讯
一、文章中要用的指令 指令作用ATUART115200,8,1,0,0之前的51通讯是9600,这里的321用的是115200,需要改一下波特率ATCWMODEXX是1代表station(设备)模式 ,X是2代表AP(路由)模式 ,X是…...

用PHP组合数组,生成笛卡尔积。写几个例子
#创作灵感# [红色,白色,黄色,蓝色] [128G,256G,512G] [国行,港版,美版,韩版] 用PHP组合数组,生成笛卡尔积。写几个例子 你可以使用嵌套的循环来生成这些数组的笛卡尔积。以下是一些示例代码: // 示例…...

软设上午题错题知识点7
软设上午题错题知识点7 1、数据流图摆脱系统的物理内容,在逻辑上描述系统的功能、输入、输出和数据存储等,是系统逻辑模型的重要组成部分。 2、HTTPS(Secure Hypertext Transfer Protocol)安全超文本传输协议。 它是一个安全通信…...
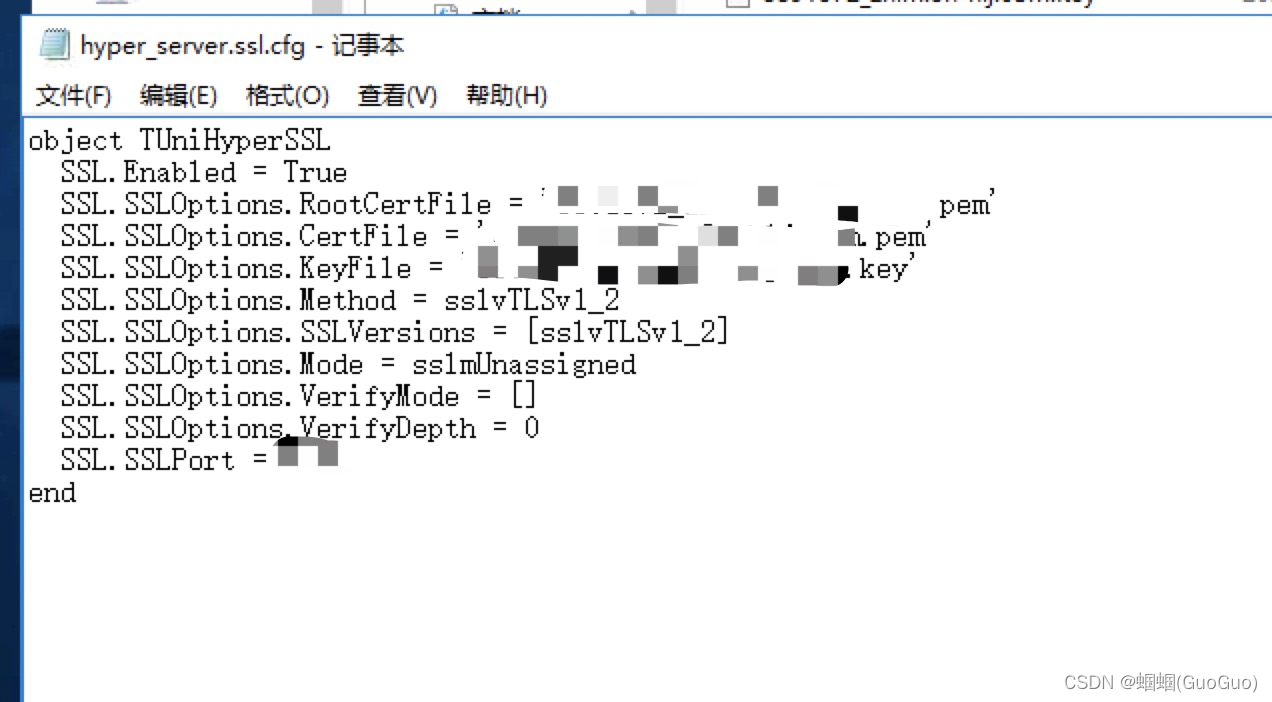
让uniGUI支持https
今天在专家的帮助下,成功的让uniGUI支持https了。 首先,去申请个**的证书。我同事去阿里申请的,申请回是一个zip文件,里面有两个文件,一个扩展是per,一个key 然后,把这两个证书文件放到uniGUI…...
iPhone怎么导出微信聊天记录?3个值得收藏的方法
随着时间的推移,微信占用的内存空间会“膨胀”得越来越大。当手机内存不足时,清理微信中的聊天记录是一个可行的方法。但是很多小伙伴觉得有些重要的聊天记录还有用,可能以后需要进行查看。 因此,他们想将一些聊天记录进行导出或…...
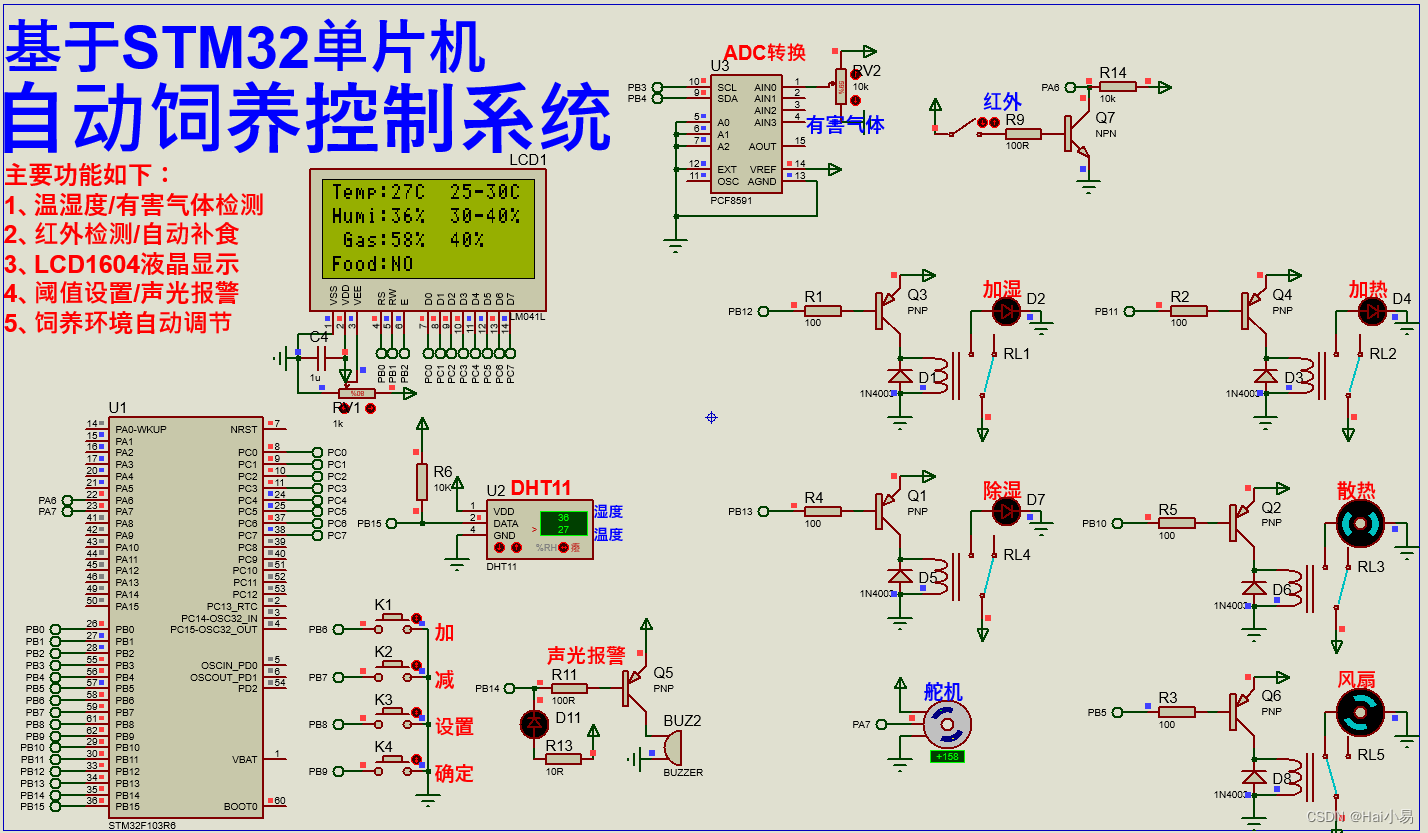
【Proteus仿真】【STM32单片机】自动饲养控制系统
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真STM32单片机控制器,使用LCD1604显示模块、红外传感器、有害气体检测模块、PCF8591 ADC模块,蜂鸣器、DHT11温湿度、SG90舵机、风扇加热加湿等。 主要功能&a…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
