数据结构:各种排序方法的综合比较
排序方法的选用应视具体场合而定。一般情况下考虑的原则有:(1)待排序的记录个数 n;(2)记录本身的大小;(3)关键字的分布情况:(4)对排序稳定性的要求等。
1.时间性能
(1) 按平均的时间性能来分,有三类排序方法:
时间复杂度为 O(nlogn)的方法有:快速排序、堆排序和归并排序,其中快速排序目前被认为是最快的一种排序方法,后两者比较,在n值较大的情况下,归并排序较堆排序更快。
时间复杂度为 O(n2)的有:插入排序、起泡排序和选择排序,其中以插入排序为最常用,特别是对于已按关键字基本有序排列的记录序列尤为如此,选择排序过程中记录移动次数最少。
时间复杂度为 O(n)的排序方法只有基数排序一种。
(2) 当待排记录序列按关键字顺序有序时,插入排序和起泡排序能达到 O(n)的时间复杂度;而对于快速排序而言,这是最不好的情况,此时的时间性能蜕化为 O(n2),因此应尽量避免。
(3) 选择排序、堆排序和归并排序的时间性能不随记录序列中关键字的分布而改变在大多数情况下,人们应事先对要排序的记录关键字的分布情况有所了解,才可对症下药,选择有针对性的排序方法。
(4) 以上对排序的时间复杂度的讨论主要考虑排序过程中所需进行的关键字间的比较次数,当待排序记录中其他各数据项比关键字占有更大的数据量时,还应考虑到排序过程中移动记录的操作时间,有时这种操作的时间在整个排序过程中占的比例更大,从这个观点考虑,简单排序的三种排序方法中起泡排序效率最低。
2.空间性能
空间性能指的是排序过程中所需的辅助空间大小。
(1) 所有的简单排序方法(包括: 插入、起泡和选择排序)和堆排序的空间复杂度均为O(1)
(2) 快速排序为 O(logn),为递归程序执行过程中栈所需的辅助空间
(3) 归并排序和基数排序所需辅助空间最多,其空间复杂度为 O(n)。
3.排序方法的稳定性能
(1) 稳定的排序方法指的是对于两个关键字相等的记录在经过排序之后,不改变它们在排序之前在序列中的相对位置。
(2) 除快速排序和堆排序是不稳定的排序方法外,其他排序方法都是稳定的。例如:对关键字序列(41,3,42,2)进行快速排序,其结果为(2,3,42,41)。
(3)“稳定性”是由方法本身决定的。一般来说,排序过程中所进行的比较操作和交换数据仅发生在相邻的记录之间,没有大步距的数据调整时,则排序方法是稳定的。
综合上述,可得下表:
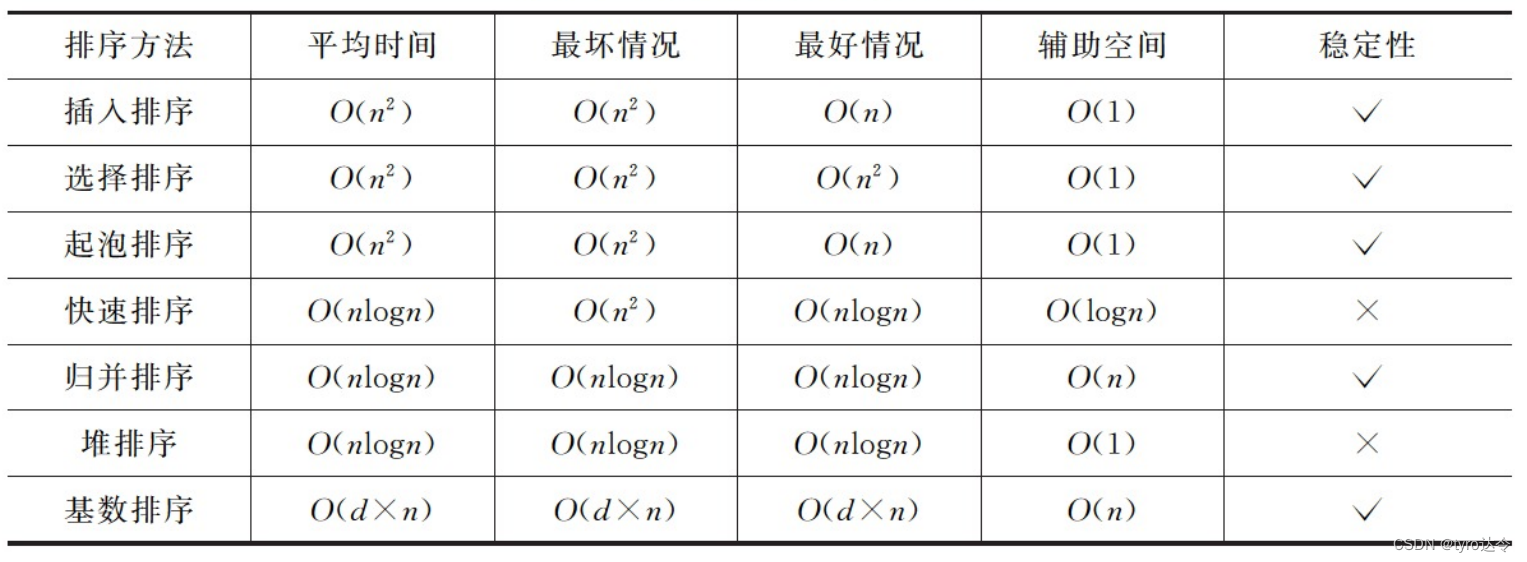
由此,在选择排序方法时,可有下列几种选择:
(1) 若待排序的记录个数 n值较小(例如 n<30),则可选用插入排序法,但若记录所含数据项较多,所占存储量大时,应选用选择排序法。反之,若待排序的记录个数n值较大时应选用快速排序法。但若待排序记录关键字有“有序”倾向时,就慎用快速排序,而宁可选用归并排序或堆排序。
(2) 快速排序和归并排序在 n 值较小时的性能不及插入排序,因此在实际应用时,可将它们和插人排序“混合”使用。如在快速排序划分子区间的长度小于某值时。转而调用插入排序;或者对待排记录序列先逐段进行插入排序,然后再利用“归并操作”进行两两归并直至整个序列有序为止。
(3) 基数排序的时间复杂度为 O(dXn),因此特别适合于待排记录数 n 值很大,而关键字“位数 d”较小的情况。并且还可以调整“基数”(如将基数定为 100 或 1000 等)以减少基数排序的趟数 d 的值。
(4) 一般情况下,进行排序的记录的“排序码”各不相同,则排序时所用的排序方法是否稳定无关紧要。但在有些情况下的排序必须选用稳定的排序方法。例如,一组学生记录已按学号的顺序有序,由于某种需要,希望根据学生的身高进行一次排序,并且排序结果应保证相同身高的同学之间的学号具有有序性。显然,在对“身高”进行排序时必须选用稳定的排序方法。
相关文章:

数据结构:各种排序方法的综合比较
排序方法的选用应视具体场合而定。一般情况下考虑的原则有:(1)待排序的记录个数 n;(2)记录本身的大小;(3)关键字的分布情况:(4)对排序稳定性的要求等。 1.时间性能 (1) 按平均的时间性能来分,有三类排序方法: 时间复杂度为 O(nlogn)的方法有:快速排序、堆排序和归并排序,其中…...
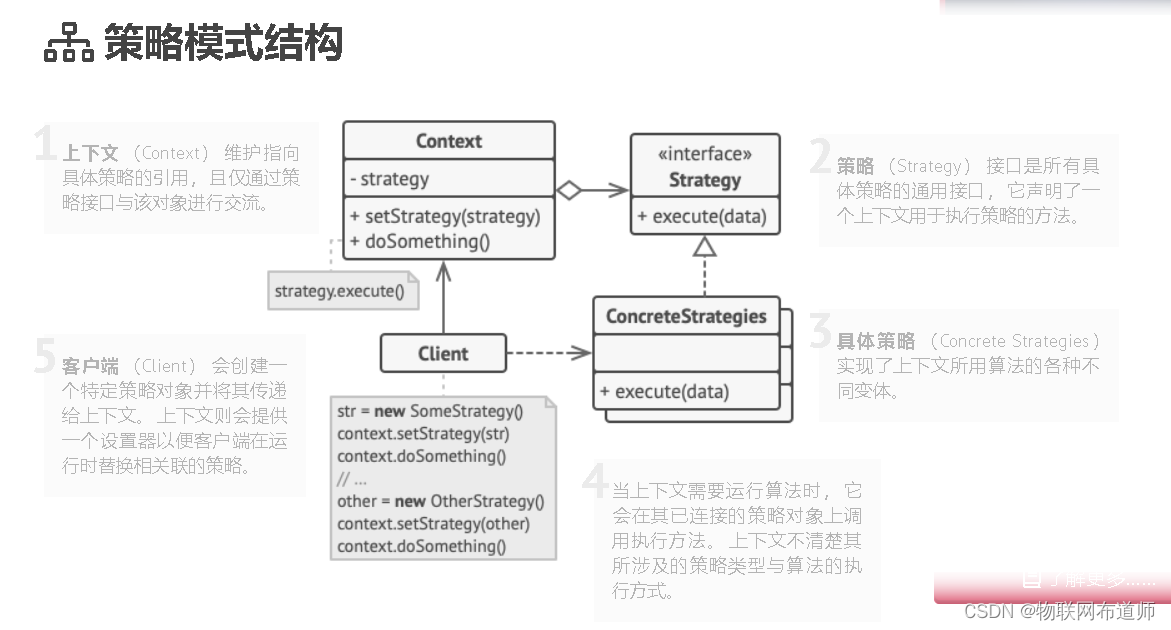
【设计模式】 策略模式介绍及C代码实现
【设计模式】 策略模式介绍及C代码实现 背景 在软件构建过程中,某些对象使用的算法可能多种多样,经常改变,如果将这些算法都编码到对象中,将会使对象变得异常复杂,而且有时候支持不使用的算法也是一个性能负担。 如何…...

【数据库】第二章 关系数据库
第二章 关系数据库 2.1关系数据结构及形式化定义 关系 域(domain) :域是一组具有相同数据类型的值的集合,可以取值的个数叫基数 笛卡尔积 :一个记录叫做一个元组(tuple),元组中每一个属性值,叫一个分量 基数&…...

oracle和mysql的分页
oracle的分页:rownum 注意:: 对 ROWNUM 只能使用 < 或 <, 用 、 >、 > 都不能返回任何数据。 rownum是对结果集的编序排列,始终是从1开始,所以rownum直接使用时不允许使用>、> 所以当查询中间部分的信息时&…...

深拷贝与浅拷贝的理解
浅拷贝的理解浅拷贝的话只会拷贝基本数据类型,例如像string、Number等这些,类似:Object、Array 这类的话拷贝的就是对象的一个指针(通俗来讲就是拷贝一个引用地址,指向的是一个内存同一份数据),也就是说当拷贝的对象数…...

Shell变量
一、变量分类 根据作用域分三种 (一)只在函数内有效,叫局部变量 (二)只在当前shell进程中有效,叫做全局变量 (三)在当前shell进程与子进程中都有效,叫做环境变量 shell进…...
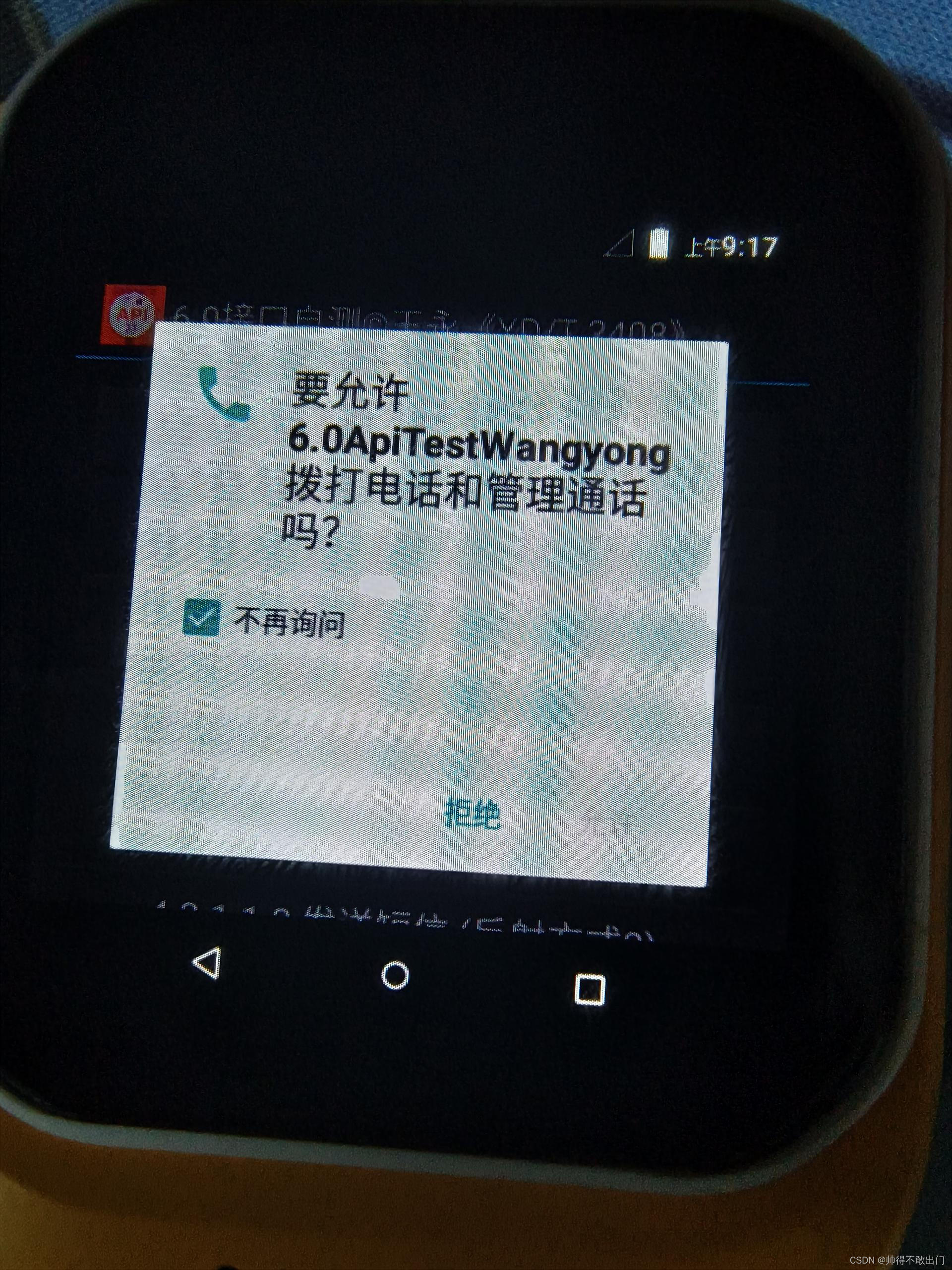
Android 8请求权限时弹窗BUG
弹窗BUG 应用使用requestPermissions申请权限时,系统会弹出一个选择窗口,可进行允许或拒绝, 此窗口中有一个”不再询问“的选择框, ”拒绝”及“允许”的按钮。 遇到一个Bug,单点击“不再询问”,“允许”这个按钮会变…...

路漫漫:网络空间的监管趋势
网络空间是“以相互依存的网络基础设施为基本架构,以代码、信息与数据的流动为环境,人类利用信息通讯技术与应用开展活动,并与其他空间高度融合与互动的空间”。随着信息化技术的发展,网络空间日益演绎成为与现实人类生存空间并存…...

洛谷 P1208 [USACO1.3]混合牛奶 Mixing Milk
最后水一篇水题题解(实在太水了) # [USACO1.3]混合牛奶 Mixing Milk ## 题目描述 由于乳制品产业利润很低,所以降低原材料(牛奶)价格就变得十分重要。帮助 Marry 乳业找到最优的牛奶采购方案。 Marry 乳业从一些奶农手…...

数据库的基本查询
注意:LIMIT的两个参数,第一个是起始位置,第二个是一次查询到多少页。注意:什么类型的数字都是可以排序的。日期的降序是从现在到以前,MySQL ENUM值如何排序?在MYSQL中,我们知道每个ENUM值都与一…...
10 分钟把你的 Web 应用转为桌面端应用
在桌面端应用上,Electron 也早已做大做强,GitHub桌面端、VSCode、Figma、Notion、飞书、剪映、得物都基于此。但最近后起之秀的 Tauri 也引人注目,它解决了 Electron 一个大的痛点——打包产物特别大。 我们知道 Electron 基于谷歌内核 Chro…...
Delphi RSA加解密(二)
dll开发环境: Delphi XE 10.1 Berlin exe开发环境: Delphi 6 前提文章: Delphi RSA加解密(一) 目录 1. 概述 2. 准备工作 2.1 下载DEMO程序 2.2 字符编码说明 3. Cryption.dll封装 3.1 接口概况 3.2 uPub.pas单元代码 3.3 uInterface.pas单元代码 3.4 特别注意 4. 主程序…...

pytorch 深度学习早停设置
当你设置早停的时候你需要注意的是你可能得在几个epoch后才开始判断早停。 早停参数设置 早停(Early Stopping)是一种常用的防止深度学习模型过拟合的方法。早停的设置需要根据具体情况进行调整,常见的做法是在模型训练过程中使用验证集&am…...
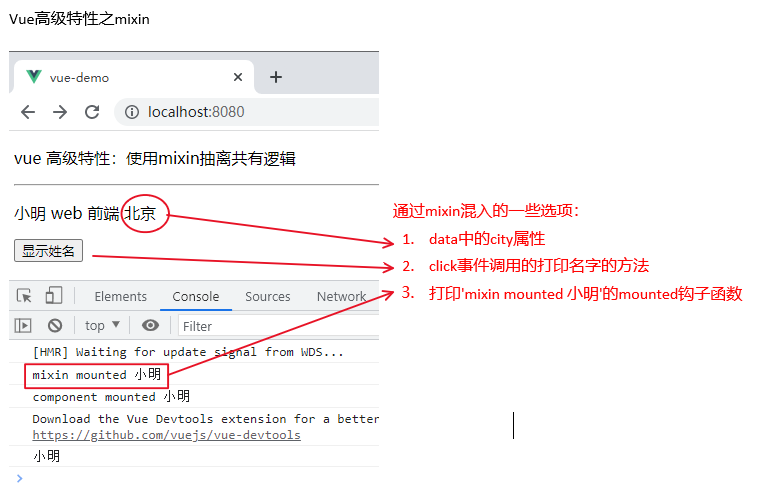
【Vue学习】Vue高级特性
1. 自定义v-model Vue中的自定义v-model指的是在自定义组件中使用v-model语法糖来实现双向绑定。在Vue中,通过v-model指令可以将表单元素的值与组件实例的数据进行双向绑定。但是对于自定义组件,如果要实现v-model的双向绑定,就需要自定义v-…...

Android 12.0 系统Settings去掉开发者模式功能
1.概述 在12.0的系统rom产品定制化开发中,在系统Settings中的关于手机的选项中,系统默认点击版本号5次会自动打开开发者模式,但是在某些产品开发过程中,禁止打开开发者模式,需要去掉开发者模式的功能,所以需要在系统Settings中查看开发者模式的相关流程代码,然后禁用掉开…...
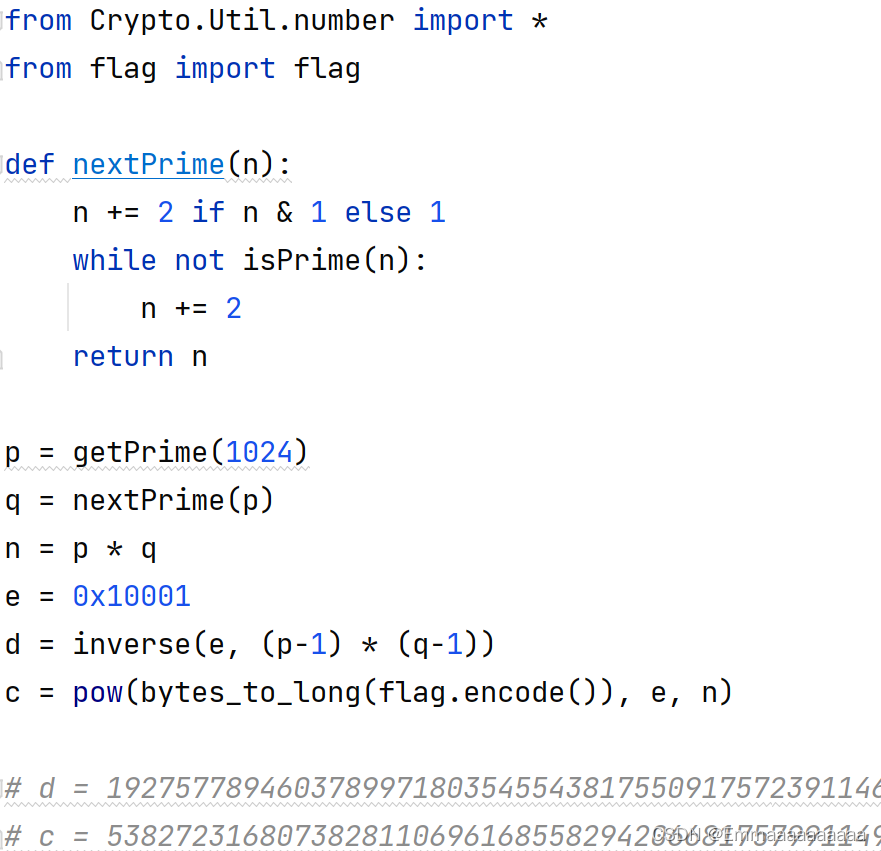
buu [NCTF2019]babyRSA 1
题目描述: 题目分析: 首先明确两个公式: e*d 1 mod (p-1)(q-1) ed1 e*d - 1 k(p-1)(q-1)想要解出此题,我们必须知道n,而要知道n,我们要知道p和q的值通过 e*d 的计算,我们知道其长度为2066位,而生成p的…...

Java:如何选择一个Java API框架
Java编程语言是一种高级的、面向对象的语言,它使开发人员能够创建健壮的、可重用的代码。Java以其可移植性和平台独立性而闻名,这意味着Java代码可以在任何支持Java运行时环境(JRE)的系统上运行。Java和Node js一样,是一种功能强大的通用编程…...

mt6735 MIC 音量的调整及原理介绍
[DESCRIPTION] MIC 音量的调整及原理介绍[SOLUTION] audio_ver1_volume_custom_default.h#define VER1_AUD_VOLUME_MIC \ 64,112,192,144,192,192,184,184,184,184,184,0,0,0,0,\ 255,192,192,180,192,192,196,184,184,184,184,0,0,0,0,\ 255,208,208,180,255,208,196,0,0,0,0,…...
【深度学习】什么是线性回归逻辑回归单层神经元的缺陷
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录逻辑回归&线性回归单层神经元的缺陷单层神经元的缺陷逻辑回归&线性回归 线性回归预测的是一个连续值, 逻辑回归给出的”是”和“否”的回答. 等…...
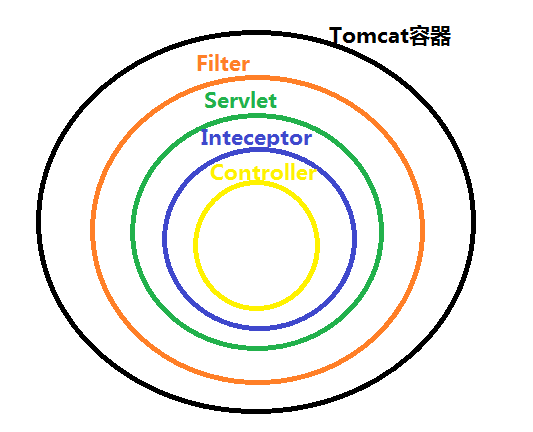
Spring拦截器
SpringMVC提供了拦截器机制,允许运行目标方法之前进行一些拦截工作或者目标方法运行之后进行一下其他相关的处理。自定义的拦截器必须实现HandlerInterceptor接口。preHandle():这个方法在业务处理器处理请求之前被调用,在该方法中对用户请求…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...
