P1196 [NOI2002] 银河英雄传说 带权并查集
[NOI2002] 银河英雄传说
题目背景
公元 580158015801 年,地球居民迁至金牛座 α\alphaα 第二行星,在那里发表银河联邦创立宣言,同年改元为宇宙历元年,并开始向银河系深处拓展。
宇宙历 799799799 年,银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征,气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。
题目描述
杨威利擅长排兵布阵,巧妙运用各种战术屡次以少胜多,难免恣生骄气。在这次决战中,他将巴米利恩星域战场划分成 300003000030000 列,每列依次编号为 1,2,…,300001, 2,\ldots ,300001,2,…,30000。之后,他把自己的战舰也依次编号为 1,2,…,300001, 2, \ldots , 300001,2,…,30000,让第 iii 号战舰处于第 iii 列,形成“一字长蛇阵”,诱敌深入。这是初始阵形。当进犯之敌到达时,杨威利会多次发布合并指令,将大部分战舰集中在某几列上,实施密集攻击。合并指令为 M i j,含义为第 iii 号战舰所在的整个战舰队列,作为一个整体(头在前尾在后)接至第 jjj 号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。
然而,老谋深算的莱因哈特早已在战略上取得了主动。在交战中,他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。
在杨威利发布指令调动舰队的同时,莱因哈特为了及时了解当前杨威利的战舰分布情况,也会发出一些询问指令:C i j。该指令意思是,询问电脑,杨威利的第 iii 号战舰与第 jjj 号战舰当前是否在同一列中,如果在同一列中,那么它们之间布置有多少战舰。
作为一个资深的高级程序设计员,你被要求编写程序分析杨威利的指令,以及回答莱因哈特的询问。
输入格式
第一行有一个整数 TTT(1≤T≤5×1051 \le T \le 5 \times 10^51≤T≤5×105),表示总共有 TTT 条指令。
以下有 TTT 行,每行有一条指令。指令有两种格式:
-
M i j:iii 和 jjj 是两个整数(1≤i,j≤300001 \le i,j \le 300001≤i,j≤30000),表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令,并且保证第 iii 号战舰与第 jjj 号战舰不在同一列。 -
C i j:iii 和 jjj 是两个整数(1≤i,j≤300001 \le i,j \le 300001≤i,j≤30000),表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。
输出格式
依次对输入的每一条指令进行分析和处理:
- 如果是杨威利发布的舰队调动指令,则表示舰队排列发生了变化,你的程序要注意到这一点,但是不要输出任何信息。
- 如果是莱因哈特发布的询问指令,你的程序要输出一行,仅包含一个整数,表示在同一列上,第 iii 号战舰与第 jjj 号战舰之间布置的战舰数目。如果第 iii 号战舰与第 jjj 号战舰当前不在同一列上,则输出 −1-1−1。
样例 #1
样例输入 #1
4
M 2 3
C 1 2
M 2 4
C 4 2
样例输出 #1
-1
1
提示
战舰位置图:表格中阿拉伯数字表示战舰编号
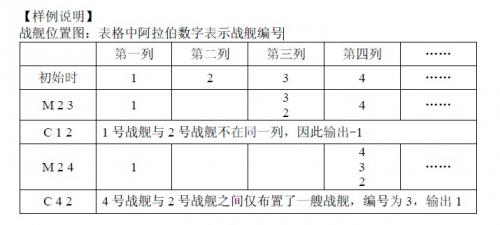
带权并查集
我一开始的代码:
#include <bits/stdc++.h>using namespace std;const int maxn=30000;int pre[maxn+5],d[maxn+5],lazy[maxn+5],num[maxn+5],ind[maxn+5];
int T;
char op;void init()
{for(int i=0;i<=maxn;i++){pre[i]=i;d[i]=0;lazy[i]=0;num[i]=1;ind[i]=0;}
}int findroot(int x)
{if(pre[x]==x) return x;int y= pre[x];int rooty=findroot(y);d[x]+= lazy[y];lazy[x]+= lazy[y];if(--ind[y]==0){lazy[y]=0;}pre[x]=rooty;ind[rooty]++;return rooty;
}
void join(int x,int y)
{int rootx=findroot(x);int rooty=findroot(y);pre[rootx]=rooty;d[rootx]+=num[rooty];lazy[rootx]+=num[rooty];num[rooty]+=num[rootx];ind[rooty]++;
}void query(int x,int y)
{int rootx=findroot(x);int rooty=findroot(y);if (rootx!=rooty){puts("-1");return;}int maxi=max(d[x],d[y]);int mini=min(d[x],d[y]);printf("%d\n", max(maxi-mini-1,0) );}
int main()
{int x,y;while(~scanf("%d",&T)){init();while(T--){scanf(" %c%d%d",&op,&x,&y);if(op=='M'){join(x,y);}else if(op=='C'){query(x,y);}}}return 0;
}
看了题解,发现不用使用lazy数组。
因为d[]维护的是当前结点相对于根结点的距离。
每个结点x的d[x]初始化时是0,只有一次机会作为根结点合并到其它根结点rooty,此时d[x]会有更新。
同时当x的父亲节点y=pre[x]指向新的父结点时,会更新d[y],之后调用findroot(x)也会更新d[x]。
#include<iostream>
#include<cmath>
using namespace std;
int f[30001],s[30001],b[30001];
int find(int o)//查找
{if(f[o]==o) return o;int k=f[o];f[o]=find(f[o]);//路径压缩s[o]+=s[k];//更新当前节点到根的距离return f[o];
}
int main()
{int n;cin>>n;for(int i=1;i<=30000;i++) {f[i]=i;s[i]=0;b[i]=1;}for(int i=1;i<=n;i++){char ch;int x,y,dx,dy;cin>>ch>>x>>y;if(ch=='M'){dx=find(x);//查找x的根dy=find(y);//查找y的根f[dx]=dy;//把x放在y后面s[dx]+=b[dy];//更新x的根到新的根的距离b[dx]+=b[dy];//更新集合大小b[dy]=b[dx];//更新集合大小}if(ch=='C'){dx=find(x);dy=find(y);if(dx!=dy){cout<<-1<<endl;continue;}//不在同一个集合中cout<<abs(s[x]-s[y])-1<<endl;//中间战舰的数量等于x到根的距离减y到根的距离减一。}}return 0;
}
总结:
- 使用并查集,当一个结点x指向的结点变化时pre[x]
无非一下两种情况: 1) x作为根结点 合并到 另一个树的根结点。
- x或其子树内结点调用查找操作,将x指向了根结点rootx。
相关文章:

P1196 [NOI2002] 银河英雄传说 带权并查集
[NOI2002] 银河英雄传说 题目背景 公元 580158015801 年,地球居民迁至金牛座 α\alphaα 第二行星,在那里发表银河联邦创立宣言,同年改元为宇宙历元年,并开始向银河系深处拓展。 宇宙历 799799799 年,银河系的两大军…...

【项目实战】快来入门Groovy的基础语法吧
一、Groovy是什么? 1.1 与Java语言的关系 下一代的Java 语言,增强Java平台的唯一的脚本语言跟java一样,它也运行在 JVM 中。支持Java平台,无缝的集成了Java 的类和库;Groovy是一种运行在JVM上的动态语言,跑在JVM中的另一种语言编译后的.groovy也是以class的形式出现的。1…...
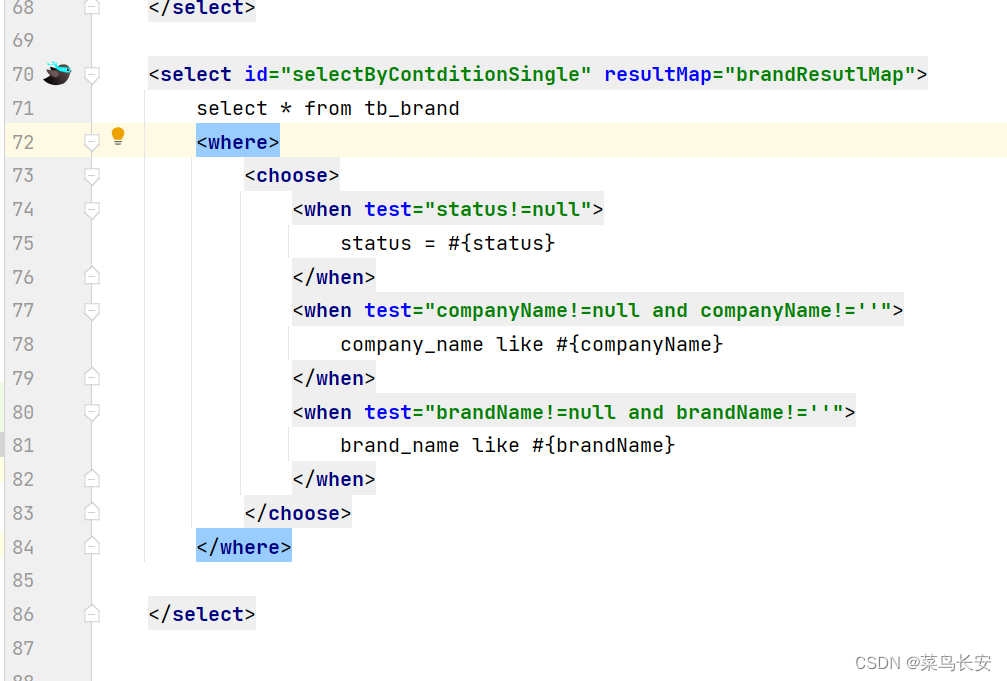
Mybatis中的动态SQL
Mybatis中的动态SQL 当存在多条件查询的SQL时,当用户某个条件的属性没有写时,就会存在问题,在test中则不能很好的运行 所以Mybatis提出了动态SQL。 即判断用户是否输入了某个属性 动态SQL中的一些问题 方法一 这个里的and是为了确保if条…...

VUE常用API
1.$set数据变了,视图没变 this.$set(targe,key,value)2.$nextTick:返回参数[函数]。是一个异步的,功能获得更新后DOM$nextTick(callback){return Promise.resolve().then(()>{callback();}) }3.$refs获取dom4.$el获取当前组件根…...

25 openEuler管理网络-使用nmcli命令配置ip
文章目录25 openEuler管理网络-使用nmcli命令配置ip25.1 nmcli介绍25.2 设备管理25.2.1 连接到设备25.2.2 断开设备连接25.3 设置网络连接25.3.1 配置动态IP连接25.3.1.1 配置IP25.3.1.2 激活连接并检查状态25.3.2 配置静态IP连接25.3.2.1 配置IP25.3.2.2 激活连接并检查状态25…...

如何安装和使用A-ops工具?
一、pip配置 1.配置信任域 pip3 config set global.trusted-host mirrors.tools.huawei.com2.配置pip源的url地址pip3 config set global.index-url http://mirrors.tools.huawei.com/pypi/simple 二、npm安装及配置 npm -v检测系统有无安装npm,如果没有的话需要配置ope…...
MySql数据库环境部署
MySql基础与Sql数据库概述基础环境的建立MYSQL数据库的连接方法MySql的默认数据库数据库端口号数据库概述 数据库(DataBase,DB)∶存储在磁带、磁盘、光盘或其他外存介质上、按定结构组织在一起的相关数据的集合。数据库管理系统〈DataBase Management S…...
极品笔记,阿里P7爆款《K8s+Jenkins》技术笔记,职场必备
前些日子从阿里的朋友那里取得这两份K8sJenkins的爆款技术笔记:《K8S(kubernetes)学习指南》《Jenkins持续集成从入门到精通》,非常高质量的干货,我立马收藏! 而今天咱们文章的主角就是这非常之干货的技术笔记:K8SJenk…...
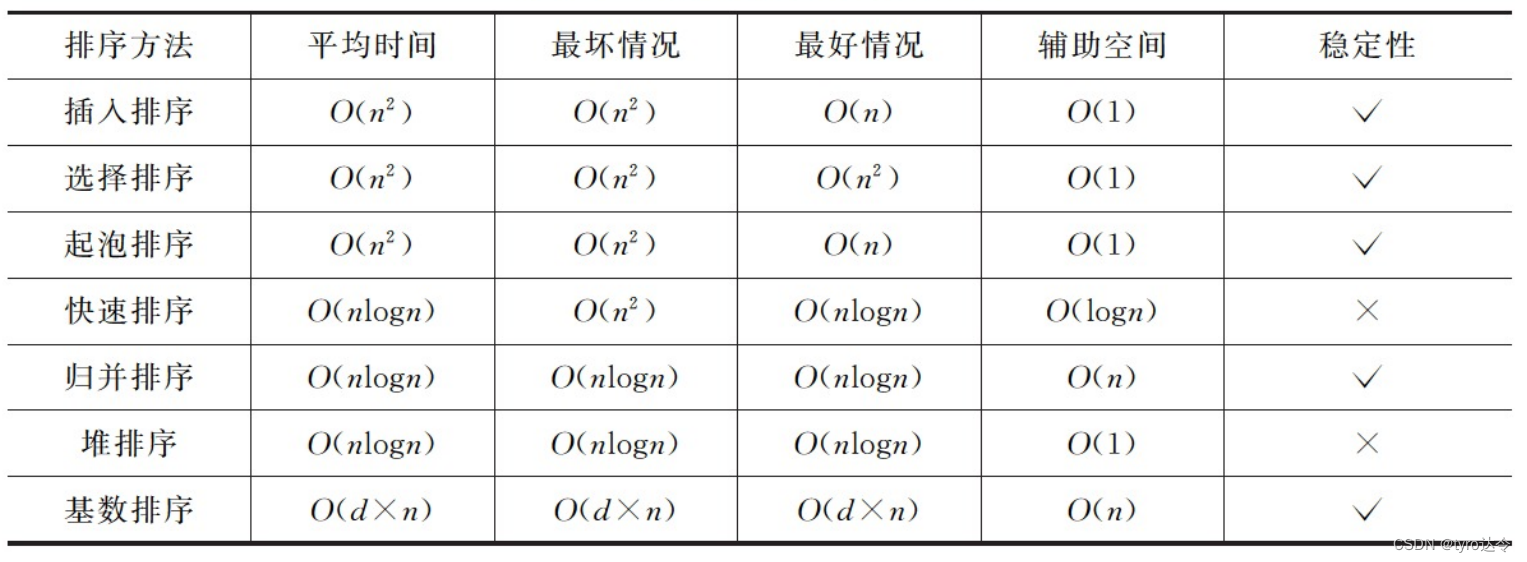
数据结构:各种排序方法的综合比较
排序方法的选用应视具体场合而定。一般情况下考虑的原则有:(1)待排序的记录个数 n;(2)记录本身的大小;(3)关键字的分布情况:(4)对排序稳定性的要求等。 1.时间性能 (1) 按平均的时间性能来分,有三类排序方法: 时间复杂度为 O(nlogn)的方法有:快速排序、堆排序和归并排序,其中…...
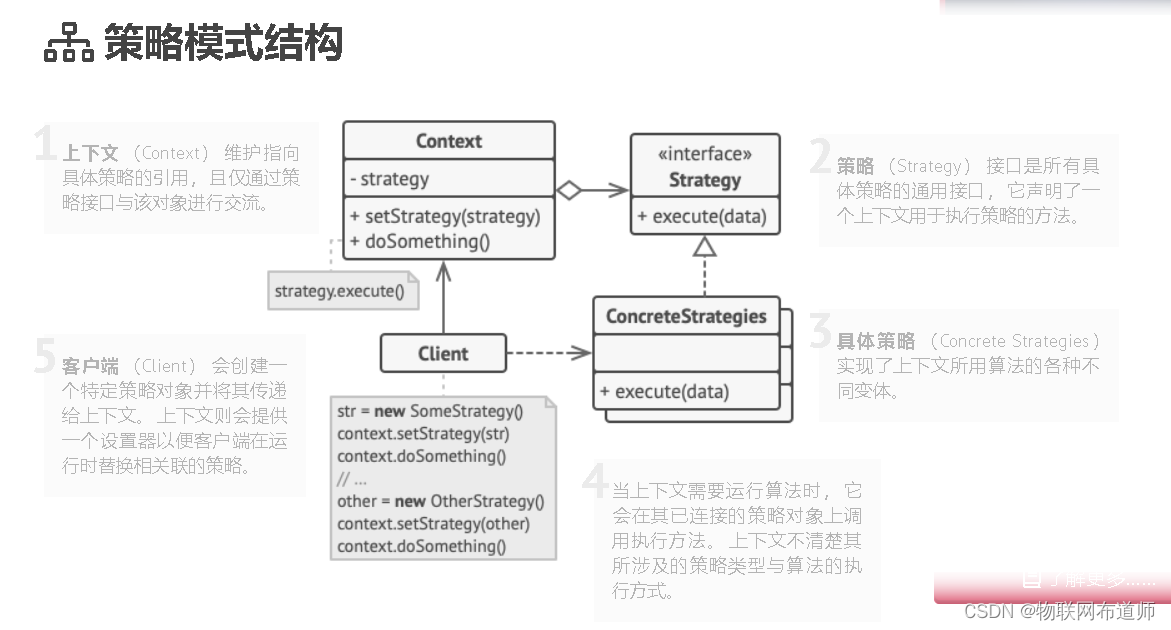
【设计模式】 策略模式介绍及C代码实现
【设计模式】 策略模式介绍及C代码实现 背景 在软件构建过程中,某些对象使用的算法可能多种多样,经常改变,如果将这些算法都编码到对象中,将会使对象变得异常复杂,而且有时候支持不使用的算法也是一个性能负担。 如何…...

【数据库】第二章 关系数据库
第二章 关系数据库 2.1关系数据结构及形式化定义 关系 域(domain) :域是一组具有相同数据类型的值的集合,可以取值的个数叫基数 笛卡尔积 :一个记录叫做一个元组(tuple),元组中每一个属性值,叫一个分量 基数&…...

oracle和mysql的分页
oracle的分页:rownum 注意:: 对 ROWNUM 只能使用 < 或 <, 用 、 >、 > 都不能返回任何数据。 rownum是对结果集的编序排列,始终是从1开始,所以rownum直接使用时不允许使用>、> 所以当查询中间部分的信息时&…...

深拷贝与浅拷贝的理解
浅拷贝的理解浅拷贝的话只会拷贝基本数据类型,例如像string、Number等这些,类似:Object、Array 这类的话拷贝的就是对象的一个指针(通俗来讲就是拷贝一个引用地址,指向的是一个内存同一份数据),也就是说当拷贝的对象数…...

Shell变量
一、变量分类 根据作用域分三种 (一)只在函数内有效,叫局部变量 (二)只在当前shell进程中有效,叫做全局变量 (三)在当前shell进程与子进程中都有效,叫做环境变量 shell进…...
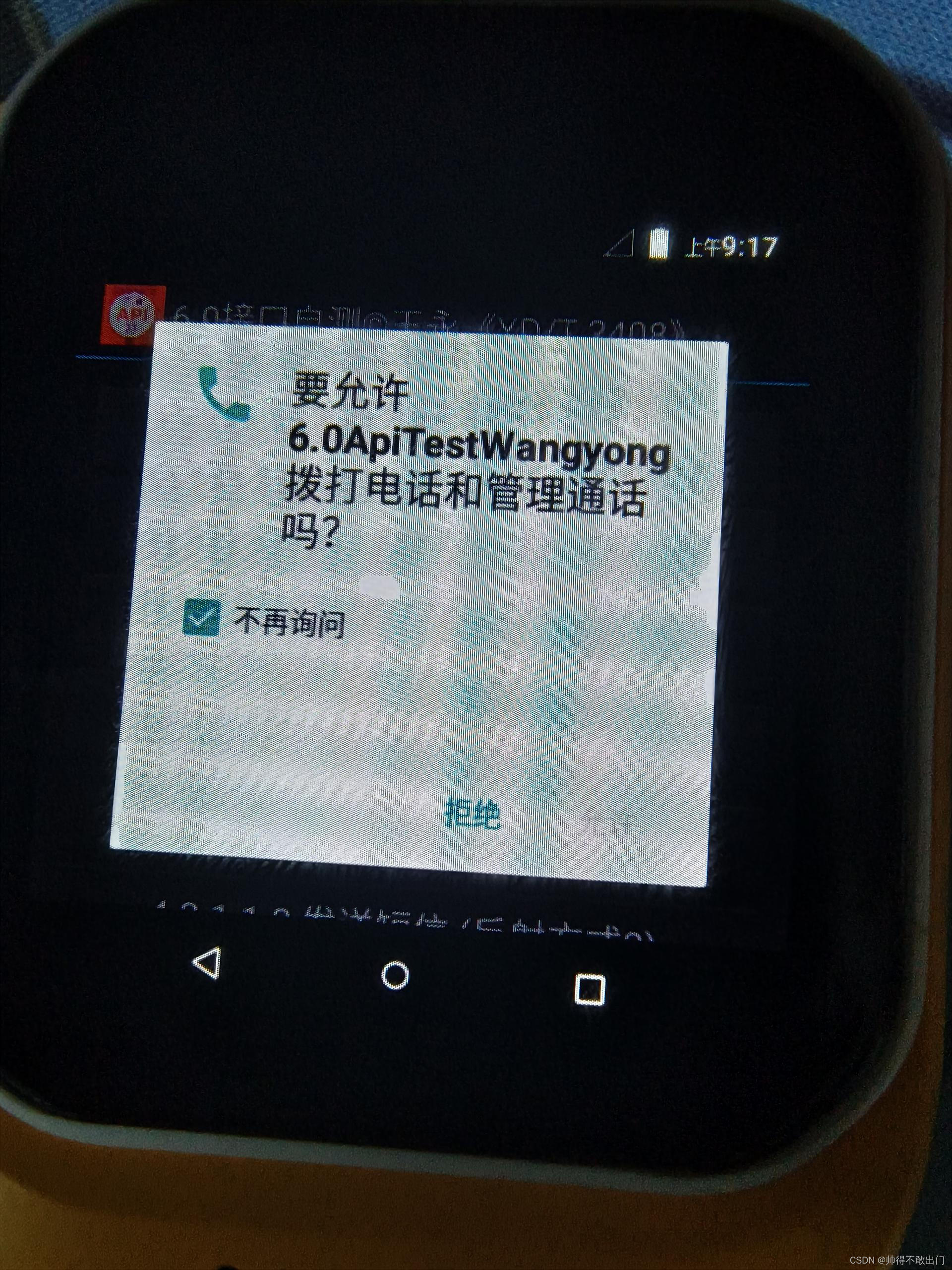
Android 8请求权限时弹窗BUG
弹窗BUG 应用使用requestPermissions申请权限时,系统会弹出一个选择窗口,可进行允许或拒绝, 此窗口中有一个”不再询问“的选择框, ”拒绝”及“允许”的按钮。 遇到一个Bug,单点击“不再询问”,“允许”这个按钮会变…...

路漫漫:网络空间的监管趋势
网络空间是“以相互依存的网络基础设施为基本架构,以代码、信息与数据的流动为环境,人类利用信息通讯技术与应用开展活动,并与其他空间高度融合与互动的空间”。随着信息化技术的发展,网络空间日益演绎成为与现实人类生存空间并存…...

洛谷 P1208 [USACO1.3]混合牛奶 Mixing Milk
最后水一篇水题题解(实在太水了) # [USACO1.3]混合牛奶 Mixing Milk ## 题目描述 由于乳制品产业利润很低,所以降低原材料(牛奶)价格就变得十分重要。帮助 Marry 乳业找到最优的牛奶采购方案。 Marry 乳业从一些奶农手…...

数据库的基本查询
注意:LIMIT的两个参数,第一个是起始位置,第二个是一次查询到多少页。注意:什么类型的数字都是可以排序的。日期的降序是从现在到以前,MySQL ENUM值如何排序?在MYSQL中,我们知道每个ENUM值都与一…...
10 分钟把你的 Web 应用转为桌面端应用
在桌面端应用上,Electron 也早已做大做强,GitHub桌面端、VSCode、Figma、Notion、飞书、剪映、得物都基于此。但最近后起之秀的 Tauri 也引人注目,它解决了 Electron 一个大的痛点——打包产物特别大。 我们知道 Electron 基于谷歌内核 Chro…...
Delphi RSA加解密(二)
dll开发环境: Delphi XE 10.1 Berlin exe开发环境: Delphi 6 前提文章: Delphi RSA加解密(一) 目录 1. 概述 2. 准备工作 2.1 下载DEMO程序 2.2 字符编码说明 3. Cryption.dll封装 3.1 接口概况 3.2 uPub.pas单元代码 3.3 uInterface.pas单元代码 3.4 特别注意 4. 主程序…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
