存储优化知识复习二详细版解析
存储优化 知识复习二
一、 选择题
1、 对数据库调优的方法中,最困难但是最有成效的是( )。
A、优化表的架构设计 B、添加内存 C、索引优化 D、查询语句优化
【参考答案】A
2、 防止与处理死锁的方法有( )。
A、尽量避免或尽快处理阻塞 B、访问数据的顺序要相同
C、让不同的连接使用相同的锁 D、提供不同的数据访问路径
【参考答案】ABCD
3、 查询语句的执行顺序为( )。
A、select B、from C、where D、group by E、having F、order by
【参考答案】BCDEAF
4、 下面属于提高数据库运行效率的方法有( )。
A、降低范式 B、增加冗余
C、少用触发器 D、多用存储过程
【参考答案】ABCD
5、 SQL Serve的性能分析工具有( )。
A、Windows 系统监视器 B、SQL Serve事件探查器 C、动态管理视图
D、性能仪表板报表 E、活动监视器 F、SQL Server 代理警报
G、数据引擎优化顾问 H、查询执行计划
【参考答案】ABCDEFGH
二、 判断题
1、一个事务读取到了另一个事务未提交的数据操作结果称为脏读。这是相当危险的,因为很可能所有的操作都被回滚。
【参考答案】对
2、当内存数据页与磁盘数据页内容不一致的时,这个内存页称为“脏页”。
【参考答案】对
3、冗余的字段会占用数据库空间,因此我们反对数据库的冗余。
【参考答案】错
4、当表的元组数超过千万时,为提高查询速度,最好将表进行水平分割。
【参考答案】对
5、当表的属性超过一百个,最好将表进行垂直分割。
【参考答案】对
6、如果学生成绩表中有学号和课程号,根据最左前缀原则,建立多列索引(学号,课程号)比(课程号,学号)更优。
【参考答案】对
7、查询分析器可确定SQL语句预执行的步骤,进而确定最耗性能的步骤。
【参考答案】对
8、避免在索引列上使用计算。语句SELECT … FROM DEPT WHERE SAL * 12 > 25000; 会导致优化器将不使用索引而使用全表扫描。
【参考答案】对
9、WHERE子句中,用>=替代>更优。如语句:SELECT * FROM EMP WHERE DEPTNO >=4 比语句: SELECT * FROM EMP WHERE DEPTNO >3 低效。
【参考答案】错
10、优化UPDATE事务时,尽量将需要更新的数据放在一张较小的表中。
【参考答案】对
三、 简答题
1、 简述索引碎片产生的原因、影响及解决方法。
原因:
数据的变动导致页分离
Insert操作导致空间不够
修改数据导致空间不够
影响:
Disk I/O增加
查询时间变长
性能下降
解决方法:
定期整理索引碎片(碎片<30% )
定期重建索引(碎片>30% )
使用填充因子(减缓碎片的产生 )
2、 试简述数据库调优可采取的方法。
架构设计
表
查询优化
•存储过程
•视图
索引优化
•覆盖查询
并发控制
•锁
•事务
存储优化
•文件组
•分区
服务器优化
•内存
•处理器亲和度
3、 索引通常采用树结构,试简述二叉树、最优二叉树、平衡二叉树、红黑树、B树、B+树的定义及区别。
二叉树:
二叉树(binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。
最优二叉树
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树。
平衡二叉树
平衡二叉树(Balanced Binary Tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
红黑树
红黑树是每个结点都带有颜色属性的二叉查找树,颜色或红色或黑色。 [3] 在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
结点是红色或黑色。
根结点是黑色。
所有叶子都是黑色。(叶子是NIL结点)
每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
从任一节结点其每个叶子的所有路径都包含相同数目的黑色结点。
B树
一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树,或者是满足下列性质的树:
1. 根结点至少有两个子女;
2. 每个非根节点所包含的关键字个数 j 满足:┌m/2┐ - 1 <= j <= m - 1;
3. 除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1,故内部子树个数 k 满足:┌m/2┐ <= k <= m ;
4. 所有的叶子结点都位于同一层。
B+树
B+树是B树的一种变形形式,B+树上的叶子结点存储关键字以及相应记录的地址,叶子结点以上各层作为索引使用。一棵m阶的B+树定义如下:
(1)每个结点至多有m个子女;
(2)除根结点外,每个结点至少有[m/2]个子女,根结点至少有两个子女;
(3)有k个子女的结点必有k个关键字。
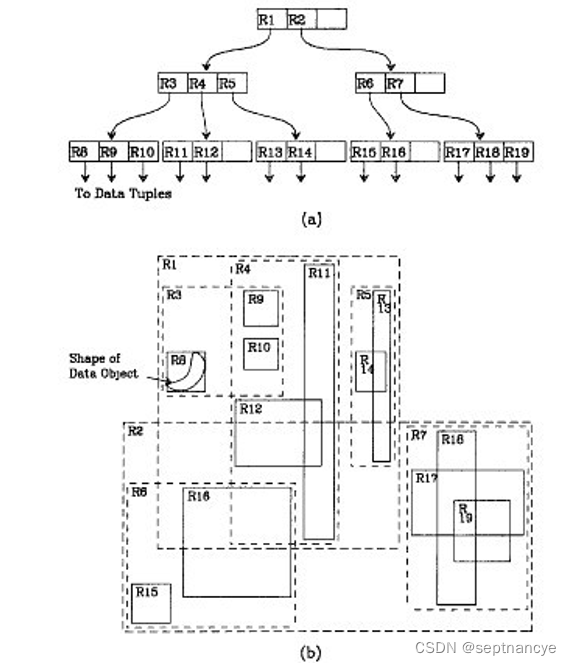
4、 试简述空间数据库的R树索引原理。
- 为实现R树结构,用最小边界矩形恰好框住各数据围成的一个区域(在图中用实线矩形表示),得到若干个最小边界矩形,如R8,R9,R10,R11等。
- 其中R8,R9,R10三个矩形距离最近,用一个更大的矩形R3(在图中用虚线矩形表示)框住三个矩形。
- 通过不断的迭代,用更大的矩形框住所有矩形。将所有大大小小的矩形存入R树中。
相关文章:
存储优化知识复习二详细版解析
存储优化 知识复习二 一、 选择题 1、 对数据库调优的方法中,最困难但是最有成效的是( )。 A、优化表的架构设计 B、添加内存 C、索引优化 D、查询语句优化 【参考答案】A2、 防止与处理死锁的方法有( )。 A、尽量避免或尽快处理阻塞 B、访…...
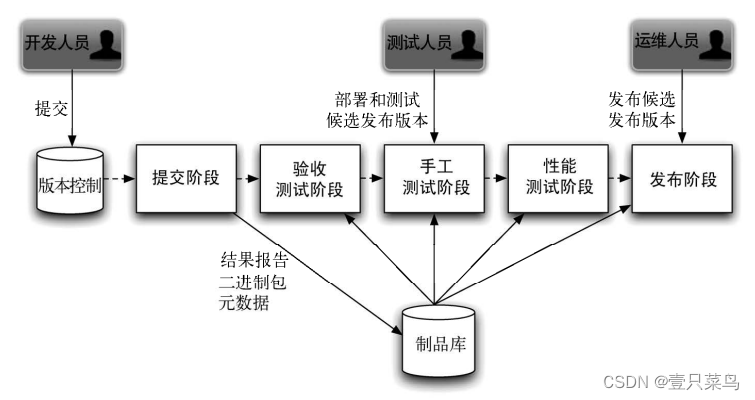
《持续交付:发布可靠软件的系统方法》- 读书笔记(七)
持续交付:发布可靠软件的系统方法(七) 第 7 章 提交阶段7.1 引言7.2 提交阶段的原则和实践7.2.1 提供快速有用的反馈7.2.2 何时令提交阶段失败7.2.3 精心对待提交阶段7.2.4 让开发人员也拥有所有权7.2.5 在超大项目团队中指定一个构建负责人 …...

Go源码实现使用多线程并发下载大文件的功能
摘要:Go语言编码实现了使用多线程并发下载文件的功能。 1. 代码流程介绍 1. 获取系统的CPU核心数量,并将其作为线程数的参考值,并打印出来。 2. 定义要下载的文件的URL、线程数和输出文件名。 3. 使用getFileSize()函数获取文件大小…...

Python基础入门例程1-NP1 Hello World!
描述 将字符串 Hello World! 存储到变量str中,再使用print语句将其打印出来。 输入描述: 无 输出描述: 一行输出字符串Hello World! 解答: str "Hello World!" print(str) 解释说明: 赋值变量&…...

前端面试题10.23
解决的最复杂的前端问题,介绍一下 最复杂的前端问题之一是浏览器兼容性,不同浏览器对网页的渲染方式存在差异,需要针对不同浏览器做兼容性处理。此外,前端性能优化也是一个复杂的问题,需要综合考虑网页加载速度、渲染…...

DYC算法开发与测试(基于ModelBase实现)
ModelBase是经纬恒润开发的车辆仿真软件,包含两个大版本:动力学版本、智能驾驶版本。动力学版包含高精度动力学模型,能很好地复现车辆在实际道路中运行的各种状态变化,可用于乘用车、商用车动力底盘系统算法开发、控制器仿真测试&…...
第四章 路由基础
目录 4.1 路由器概述 4.1.1 路由器定义 4.1.2 路由器工作原理 4.1.3 路由表的生成方式 (1)直连路由 (2)静态路由 (3)动态路由 4.1.4 路由器的接口 (1)配置接口 ࿰…...
Java逻辑运算符(、||和!),Java关系运算符
逻辑运算符把各个运算的关系表达式连接起来组成一个复杂的逻辑表达式,以判断程序中的表达式是否成立,判断的结果是 true 或 false。 逻辑运算符是对布尔型变量进行运算,其结果也是布尔型,具体如表 1 所示。 表 1 逻辑运算符的用…...
三个设备文件
...
Java赋值运算符(=)
赋值运算符是指为变量或常量指定数值的符号。赋值运算符的符号为“”,它是双目运算符,左边的操作数必须是变量,不能是常量或表达式。 其语法格式如下所示: 变量名称表达式内容 在 Java 语言中,“变量名称”和“表达式…...
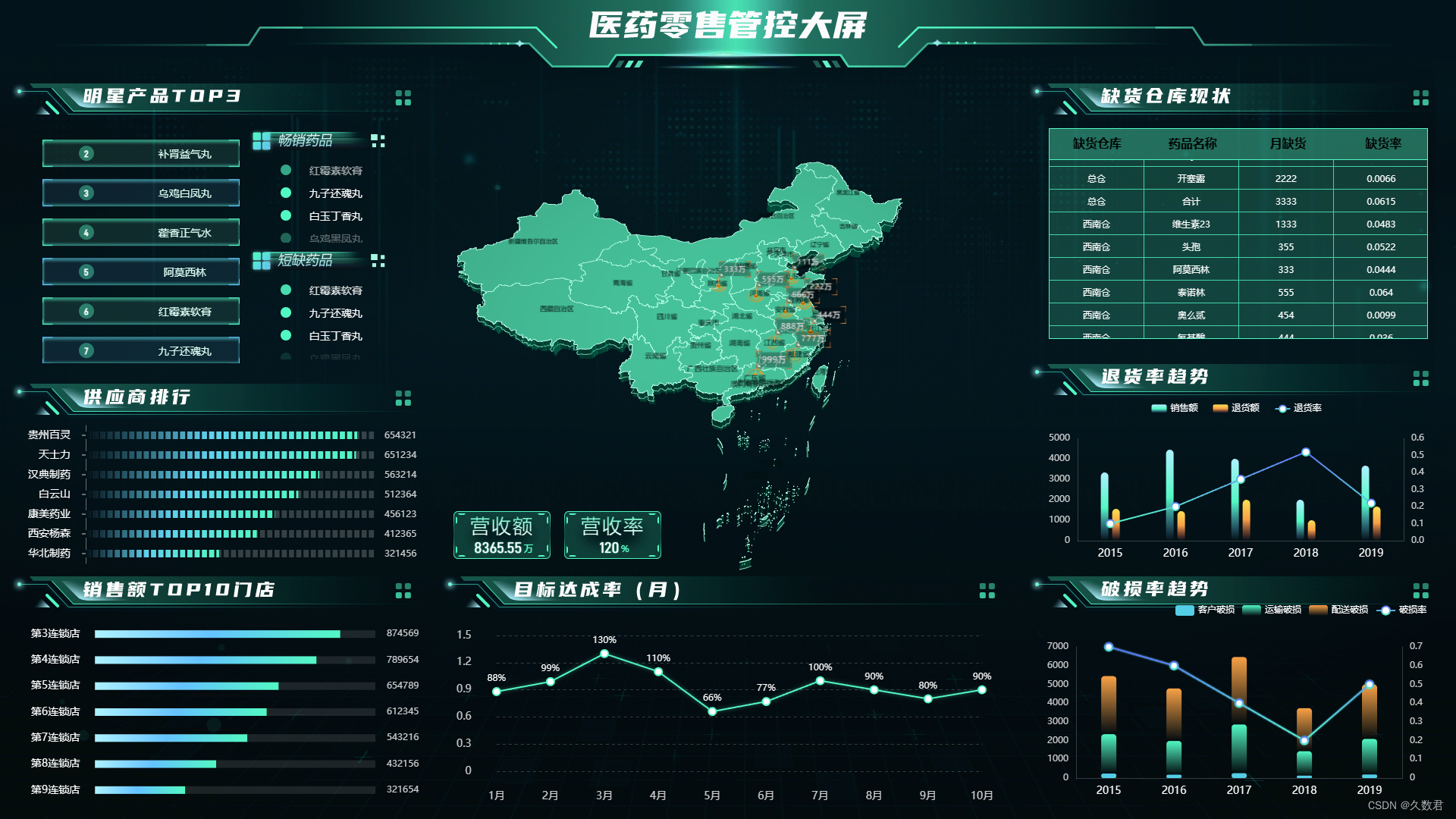
提升药店效率:山海鲸医药零售大屏的成功案例
在医药行业中,特别是医药零售领域,高效的药品管理和客户服务至关重要。随着科技的飞速发展,数字化解决方案已经成为提高医药零售管控效率的有效工具之一。其中,医药零售管控大屏作为一种强大的工具,正在以独特的方式改…...
)
使用Fragement(碎片)
一、Fragment简介 屏幕大小的差距可能会使同样的界面在不同设备上显示出不同的效果,为了能同时兼顾到手机和平板电脑的开发,从Android3.0版本开始提供了Fragment。 Fragment(碎片)是一种嵌入在Activity中的UI片段,它…...
)
种花问题(Python题目)
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。 给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 …...

STM32入门F4
学习资料:杨桃电子,官网:洋桃电子 | 杜洋工作室 www.doyoung.net 嵌入式开发核心宗旨:以最适合的性能、功能、成本来完成最有性价比的产品开发。 1.为什么要学F407 STM32F103系列与STM32F407系列对照表: 2.F4系列命…...
【30】c++设计模式——>状态模式
状态模式概述 状态模式是一种行为型设计模式,它可以让一个对象在其内部状态发生变化时更改其行为。通过将每个状态封装成一个独立的类,我们可以使状态之间互相独立,并且使得状态的切换变得更加灵活、可扩展。(多个状态之间可以相…...

中文编程开发语言编程实际案例:程序控制灯电路以及桌球台球室用这个程序计时计费
中文编程开发语言编程实际案例:程序控制灯电路以及桌球台球室用这个程序计时计费 上图为:程序控制的硬件设备电路图 上图为:程序控制灯的开关软件截图,适用范围比如:台球厅桌球室的计时计费管理,计时的时候…...

【python】高斯日记
题目: """ 题目描述: 高斯出生于1777年4月30日,记作1777-4-30。在此基础上,我们希望你写一个程序,给定一个数字n,表示从高斯出生的那天算起的第n天,输出这一天的具体日期。例如&…...

[论文笔记]MobileBERT
引言 今天带来一篇关于量化的论文MobileBERT,题目翻译过来是:一种适用于资源有限设备的紧凑型任务无关BERT模型。模型的简称是MobileBERT,意思是作者的这个BERT模型可以部署到手机端。 本篇工作,作者提出了MobileBERT用于压缩和加速BERT模型。与原始BERT一样,MobileBERT…...
【Spring Cloud】如何确定微服务项目的Spring Boot、Spring Cloud、Spring Cloud Alibaba的版本
文章目录 1. 版本选择2. 用脚手架快速生成微服务的pom.xml3. 创建一个父工程4. 代码地址 本文描述如何确定微服务项目的Spring Boot、Spring Cloud、Spring Cloud Alibaba的版本。 1. 版本选择 我们知道Spring Boot、Spring Cloud、Spring Cloud Alibaba的版本选择一致性非常重…...
Power BI 傻瓜入门 1. 数据分析术语:Power BI风格
本章内容包括: 了解Power BI可以处理的不同类型的数据了解您的商业智能工具选项熟悉Power BI术语 数据无处不在。从你醒来的那一刻到你睡觉的时候,某个系统会代表你收集数据。即使在你睡觉的时候,也会产生与你生活的某些方面相关的数据。如…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
