[论文笔记]MobileBERT
引言
今天带来一篇关于量化的论文MobileBERT,题目翻译过来是:一种适用于资源有限设备的紧凑型任务无关BERT模型。模型的简称是MobileBERT,意思是作者的这个BERT模型可以部署到手机端。
本篇工作,作者提出了MobileBERT用于压缩和加速BERT模型。与原始BERT一样,MobileBERT也是任务无关的,即它仅需简单的微调就能广泛地应用于不同的下游任务。本质上,MobileBERT是一个精简版的BERT-large,配备了瓶颈结构(bottleneck structure)和精心设计的自注意力和前馈网络之间的平衡。
要训练MobileBERT,作者首先训练一个特别的教师模型,一个集成了倒置瓶颈的BERT-large模型。然后,将知识从教师模型转移到MobileBERT上。
总体介绍
BERT自提出来之后在各种NLP任务上的效果惊人,但由于BERT的规模较大,存在参数量过大和高延迟问题,使它不可能部署到资源受限的移动设备上,来进行手机上的机器翻译、对话管理等。
已经有一些工作将BERT压缩为任务相关的紧凑模型。但还没有任何工作来构建一个任务无关的轻量级预训练模型,即一个可以像原始的BERT一样在不同的下游任务上进行通用微调的模型。本篇工作,作者提出MobileBERT来填补这个空白。实际上,任务无关的BERT压缩是可行的。
任务相关的压缩需要先将原始大BERT模型微调为任务相关的教师模型,然后进行蒸馏。这个过程比直接微调任务无关的紧凑模型更复杂,且成本更高。
但获得一个任务无关的紧凑BERT可能没有想象的那么简单,比如简单地选择一个更窄或更浅的BERT模型&#
相关文章:

[论文笔记]MobileBERT
引言 今天带来一篇关于量化的论文MobileBERT,题目翻译过来是:一种适用于资源有限设备的紧凑型任务无关BERT模型。模型的简称是MobileBERT,意思是作者的这个BERT模型可以部署到手机端。 本篇工作,作者提出了MobileBERT用于压缩和加速BERT模型。与原始BERT一样,MobileBERT…...
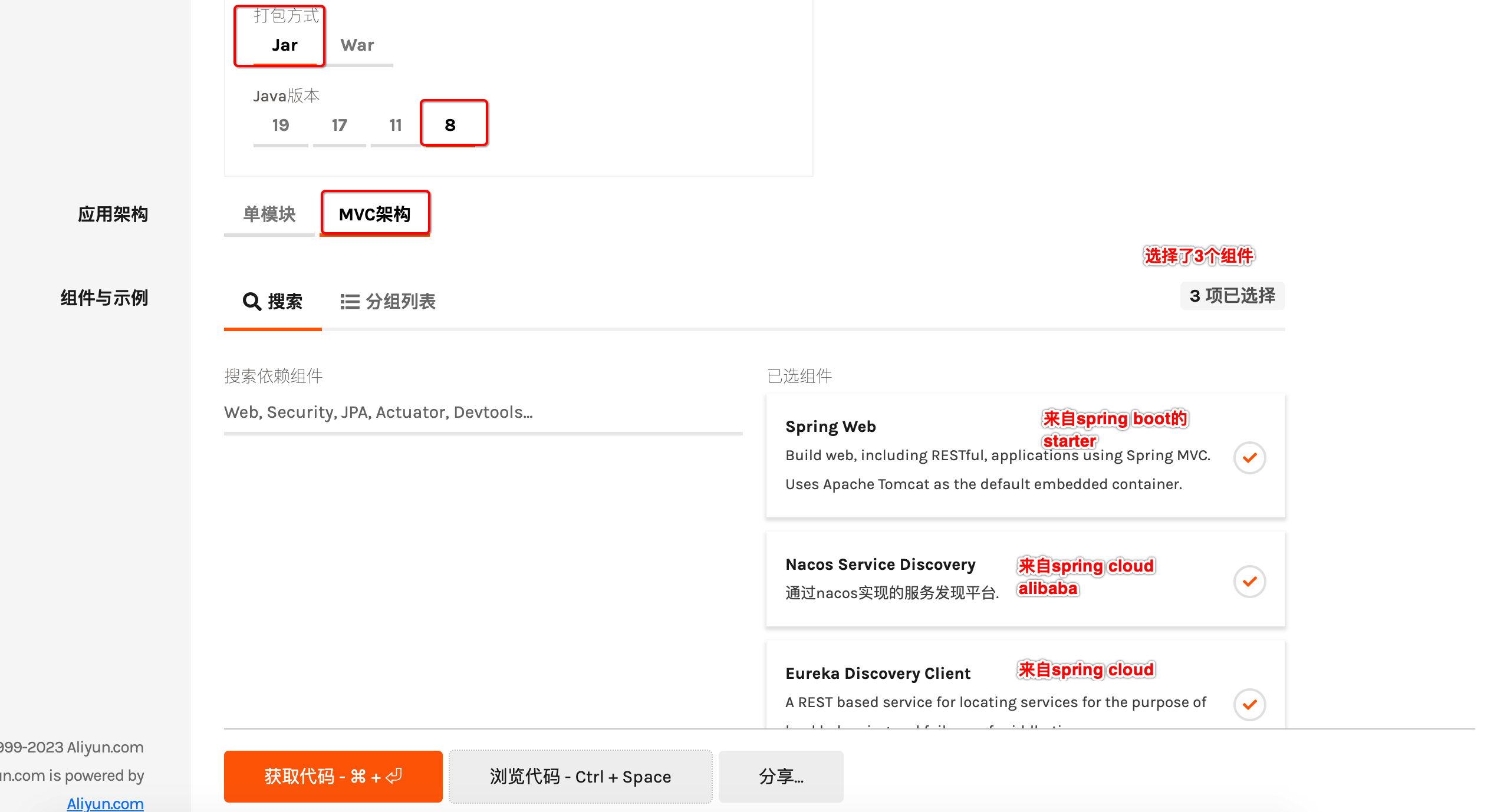
【Spring Cloud】如何确定微服务项目的Spring Boot、Spring Cloud、Spring Cloud Alibaba的版本
文章目录 1. 版本选择2. 用脚手架快速生成微服务的pom.xml3. 创建一个父工程4. 代码地址 本文描述如何确定微服务项目的Spring Boot、Spring Cloud、Spring Cloud Alibaba的版本。 1. 版本选择 我们知道Spring Boot、Spring Cloud、Spring Cloud Alibaba的版本选择一致性非常重…...
Power BI 傻瓜入门 1. 数据分析术语:Power BI风格
本章内容包括: 了解Power BI可以处理的不同类型的数据了解您的商业智能工具选项熟悉Power BI术语 数据无处不在。从你醒来的那一刻到你睡觉的时候,某个系统会代表你收集数据。即使在你睡觉的时候,也会产生与你生活的某些方面相关的数据。如…...

【C++和数据结构】位图和布隆过滤器
目录 一、位图 1、位图的概念 2、位图的实现 ①、基本结构 ②、set ③、reset: ④、test ⑤、问题: ⑥、位图优缺点及应用: ⑦、完整代码及测试 二、布隆过滤器 1、布隆过滤器的提出 2、布隆过滤器的实现 ①、基本结构 ②…...

Mybatis分页
本文主要讲解Mybatis分页相关的技术分享,如果觉得不错的话,就点个赞吧。。。。 Mybatis分页主要有2种类型: 一、物理分页: 1、定义: 物理分页是在数据库层面进行的分页,即通过SQL语句直接从数据库中查询…...
手写SVG图片
有时候QT中可能会需要一些简单的SVG图片,但是网上的质量参差不齐,想要满意的SVG图片,我们可以尝试直接手写的方法. 新建文本文档,将以下代码复制进去,修改后缀名为.svg,保存 <?xml version"1.0" encoding"utf-8"?> <svg xmlns"http://www…...
LVS负载均衡及LVS-NAT模式
一、集群概述 1.1 集群的背景 集群定义:为解决某个特定问题将多个计算机组合起来形成一个单系统 集群目的:为了解决系统的性能瓶颈 集群发展历史: 垂直扩展:向上扩展,增加单个机器的性能,即升级硬件 水…...

【Java集合类面试八】、 介绍一下HashMap底层的实现原理
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官: 介绍一下HashMap底层的…...
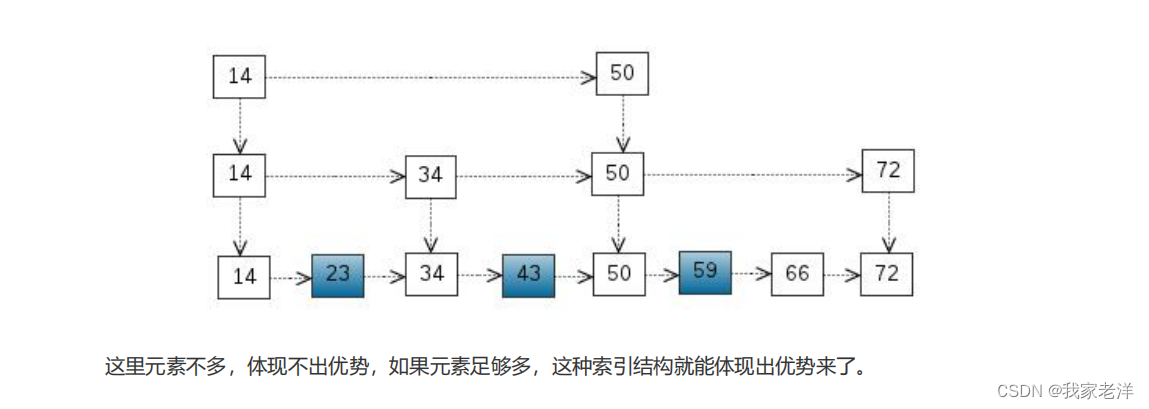
linux 安装操作 redis
1、redis概述和安装 1.1、安装redis 1. 下载redis 地址 https://download.redis.io/releases/ 2. 将 redis 安装包拷贝到 /opt/ 目录 3. 解压 tar -zvxf redis-6.2.1.tar.gz4. 安装gcc yum install gcc5. 进入目录 cd redis-6.2.16. 编译 make7. 执行 make install 进…...
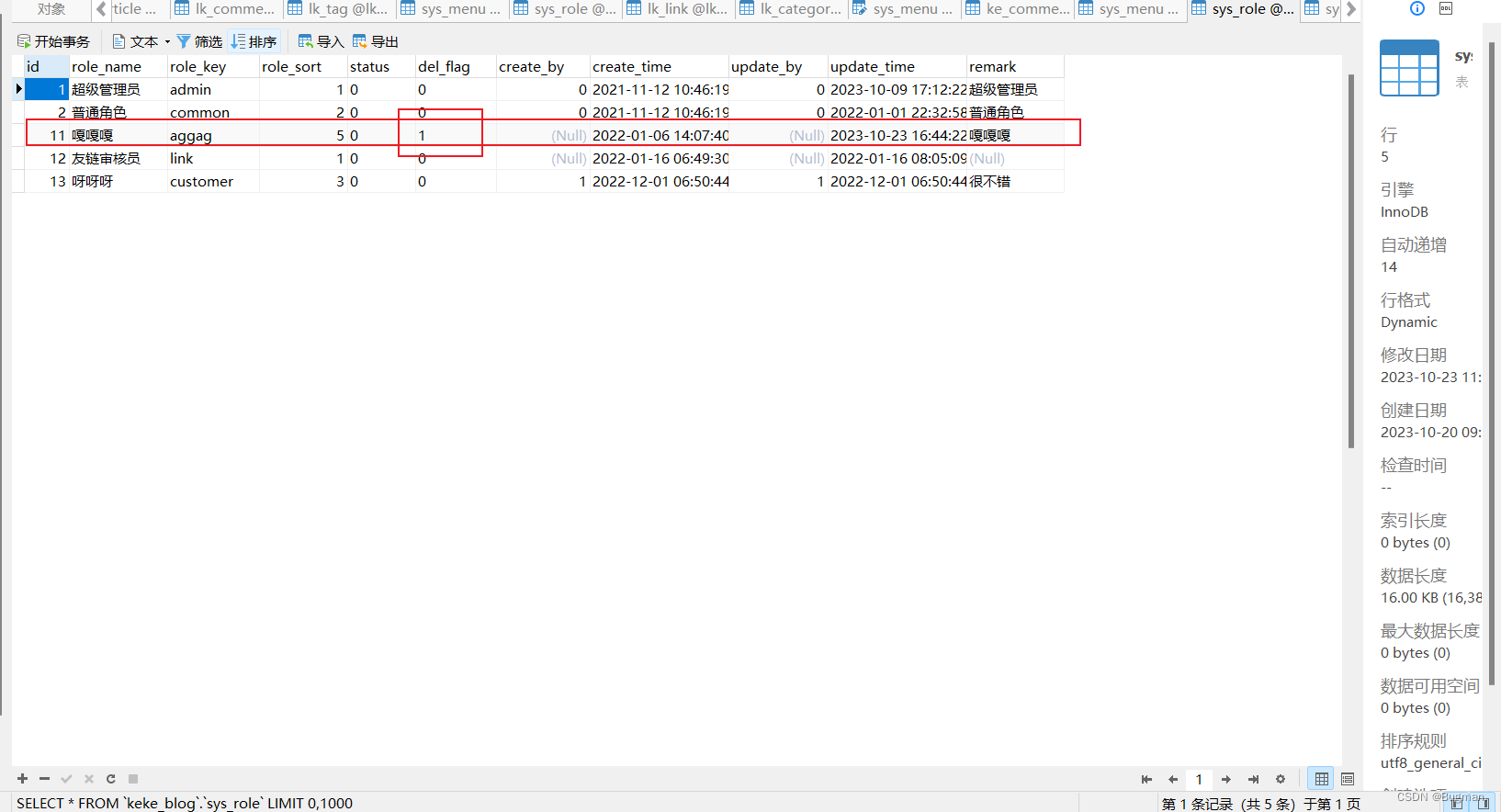
博客后台模块续更(五)
十一、后台模块-菜单列表 菜单指的是权限菜单,也就是一堆权限字符串 1. 查询菜单 1.1 接口分析 需要展示菜单列表,不需要分页。可以针对菜单名进行模糊查询。也可以针对菜单的状态进行查询。菜单要按照父菜单id和orderNum进行排序 请求方式 请求路径…...

手写一个PrattParser基本运算解析器4: 简述iOS的编译过程
点击查看 基于Swift的PrattParser项目 iOS项目的编译过程与PrattParser解析器 前面三篇我们看到了PrattParser解析器的工作原理, 工作过程, 我们了解到PrattParser解析器实际上是模拟了编译过程中的 词法分析 、语法分析 、语义分析 、 中间代码生成 这几个编译前端过程. 那么P…...

【Java集合类面试六】、 HashMap有什么特点?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:HashMap有什么特点&…...
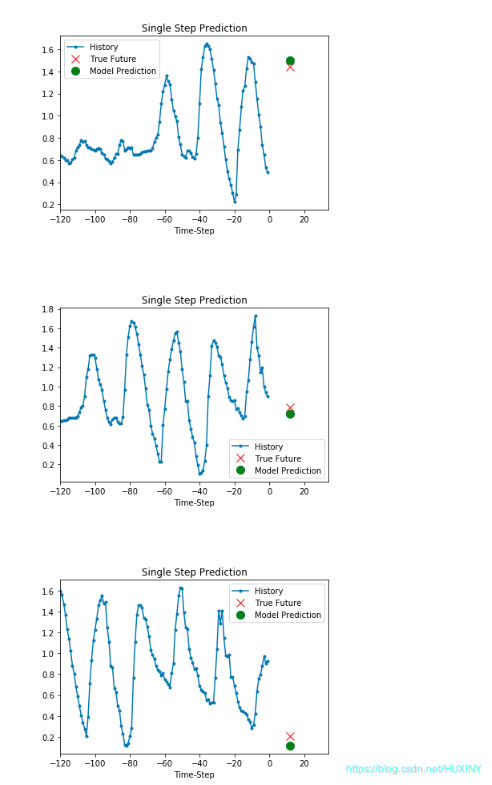
基于LSTM的天气预测 - 时间序列预测 计算机竞赛
0 前言 🔥 优质竞赛项目系列,今天要分享的是 机器学习大数据分析项目 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/po…...
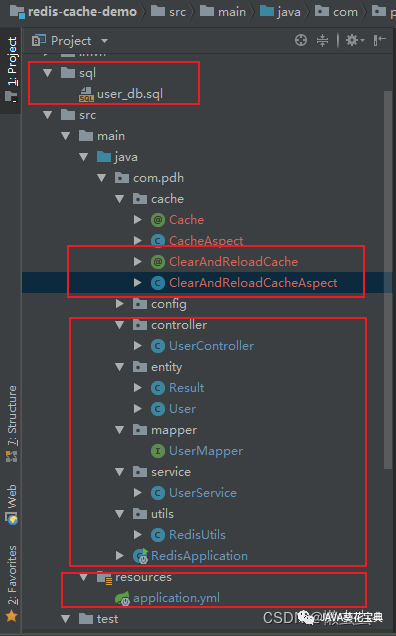
SpringBoot AOP + Redis 延时双删功能实战
一、业务场景 在多线程并发情况下,假设有两个数据库修改请求,为保证数据库与redis的数据一致性,修改请求的实现中需要修改数据库后,级联修改Redis中的数据。 请求一:A修改数据库数据 B修改Redis数据 请求二ÿ…...

【Java集合类面试七】、 JDK7和JDK8中的HashMap有什么区别?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:JDK7和JDK8中的HashMap有…...

el-tree 获取过滤后的树结构
正常来说element框架应该返回的,但实际上没有,只能自己处理了 递归处理,思路就是赋值,如果是自己过滤到的数据就push进去,不是就不要 let newCheckTree [] let tree get_tree(treeData,newCheckTree); //获取过滤…...

Windows连接SFTP服务
最近有个新需求需要通过SFTP方式连接到一个FTP中下载相关内容 1.使用命令行方式 在cmd中使用如下命令 sftp -P [port] [username]ip #示例 sftp -P 666 ftp123.123.123.123然后弹出的提示输入yes,再输入密码就可以了。 2.使用资源管理器方式 普通FTP可以使用资源…...
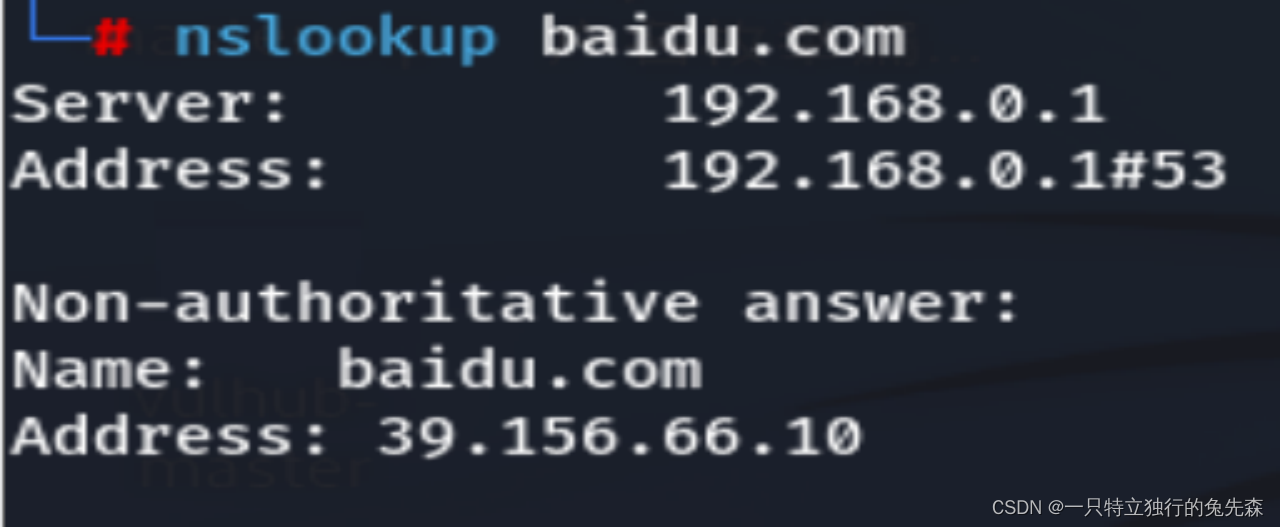
《红蓝攻防对抗实战》五.内网探测协议出网之DNS协议探测出网
DNS(Domain Name System)即域名解析系统,可将域名解析到对应访问IP。下面我们还是以系统自带命令为案例,进行演示DNS协议探测出网。 目录 一.Windows系统探测DNS协议出网 二.Linux系统探测DNS协议出网 1. Dig命令 2.Nslookup命…...

计算机算法分析与设计(18)---回溯法(介绍、子集和问题C++代码)
文章目录 一、回溯法介绍二、子集和问题2.1 知识概述2.2 代码编写 一、回溯法介绍 1. 回溯法(back tracking)是一种选优搜索法,又称为试探法,有“通用的解题法”之称,按选优条件向前搜索,以达到目标。但当探…...
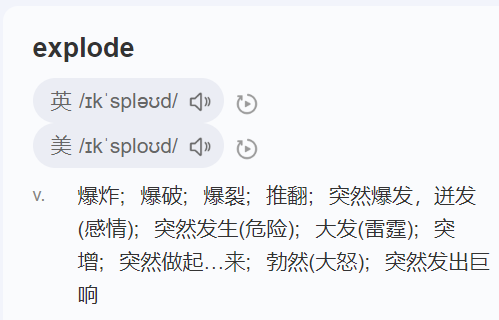
[Hive] explode
在 Hive 中,explode 函数用于将数组(Array)或者Map类型的列拆分成多行, 每个元素或键值对为一行。这允许我们在查询中对数组或 Map 进行扁平化操作。 下面是使用 explode 函数的示例: 假设我们有一个包含数组字段的表…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
