【C++和数据结构】位图和布隆过滤器

目录
一、位图
1、位图的概念
2、位图的实现
①、基本结构
②、set
③、reset:
④、test
⑤、问题:
⑥、位图优缺点及应用:
⑦、完整代码及测试
二、布隆过滤器
1、布隆过滤器的提出
2、布隆过滤器的实现
①、基本结构
②、三个Hash仿函数实现
③、 set
④、 test
⑤、 删除
⑥、完整代码及测试
⑦、 优缺点
一、位图
1、位图的概念
1. 面试题给 40 亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这 40 亿个数中。【腾讯】查找一个数在不在,其实就是key模型,那常见的几种解法如下:
- 1. 遍历,时间复杂度O(N)
- 2. 排序(O(NlogN)),利用二分查找: logN
- 3. 位图解决
前两个方案的问题:数据量太大,放不到内存中。
我们可以先考虑40亿个不重复的无符号整数占多少空间?10亿个字节是1个G,而40亿个整数,一个整数4个字节,即需要160亿(9个0)个字节,即需要16G,这些数据太占空间了,内存根本存不下。位图是如何解决的呢?
所谓位图,就是用每一bit位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用 来判断某个数据存不存在的。数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一 个二进制比特位来代表数据是否存在的信息,如果二进制比特位为 1 ,代表存在,为0 代表不存在。(位图是直接定址法的一种)而40亿个数据,我们起码要开42亿个空间,为什么?假如有一个数是4200000000,你要映射到哪个位置?我们开空间是要开数据的范围,才能满足全部映射进去。那我们直接开2^32个空间(这里说的每个位置就是比特位,2^32≈42亿9千万,因为位图就是每个位置存的bit位),来对所有数直接定址法建立映射关系,即我们开辟42亿9千万个bit位,先把42亿9千万看成字节,则其≈4G,而4G≈4000M(或者MB),而这里是比特位,故要除以8,4000/8=500M,故位图存储占用500M即可,这既节省了空间,效率又很高(效率高,因为直接定址法没哈希冲突)
2、位图的实现
①、基本结构
位图的初始化应该是开多少个比特位,因为位图就是利用存比特位来节省的空间,你传的N也是比特位,其次是vector的类型是int,因为类型不支持是比特位的
class bitset
{
public:bitset(size_t N){//N代表要开多少比特位(简称:位)_bits.resize(N / 32 + 1, 0);_num = N;}private://int* _bits;std::vector<int> _bits;size_t _num; //表示存了多少个比特位,映射存储的多少个数据
};_bits.resize(N / 32 + 1, 0);为什么要N / 32 + 1 呢?
因为vector的resize开空间是以整形为单位的,而位图的每个位置存的都是一个比特位,而一个整形32个比特位,N代表的是比特位的位数,则N/32得到的是整形的个数,但是还需+1,为什么?比如N=100,100/32=3,那意思就是开3个整形,即32*3=96个位,但是100还是没位置放,你就开了96个位(同理97,98...都没位置),为了避免这个问题我们会+1,即多开一个整形,那最多只会浪费31个位
②、set
功能:把第x个位设置为1,表示这个位存在
void set(size_t x)
{//把第x位设置为1,表示此位置存在size_t index = x / 32; //算出映射的位置在第几个整数size_t pos = x % 32; //算出x在整数的第几个位_bits[index] |= (1 << pos); //对于这个整数第pos的位置或1//1<<pos表示先把1移动到和pos相同位置的比特位上,因为pos=几,1就会左移几位//|=表示是或,即除了pos位置的位要变成1,其余位置都不受影响
}其实就是考察怎么把一个整数的某个位变成1,还不影响其他的31位
小端机的左移是向左 , 大端机的左移是向右
这是c语言设计的bug,历史遗留问题,易让人误导,计算机技术发展百花齐放,再融合统一
③、reset:
功能:把第x个位置成0,表示这个位不存在
void reset(size_t x)
{//把第x位设置为0,表示此位置不存在size_t index = x / 32; //算出映射的位置在第几个整数size_t pos = x % 32; //算出x在整数的第几个位_bits[index] &= ~(1 << pos); //对于这个整数第pos的位置与0
}
④、test
功能:判断第x位在不在(即判断x所映射的位是否为1)
//判断x在不在(也就是说x映射的位是否为1)
bool test(size_t x)
{size_t index = x / 32; //算出映射的位置在第几个整数size_t pos = x % 32; //算出x在整数的第几个位return _bits[index] & (1 << pos); //结果非0为真,0则为假
}
⑤、问题:
理论上这40亿个数不可能存在内存当中,应该存在文件中,那我们就要去读文件,40亿个数因为要按范围开,故要开42亿9千万的空间,怎么开这么大的空间?常见方法如下:
①、bitset bs(-1); //因为位图的构造函数参数是size_t,那-1若看为无符号数就是整形的最大值
②、bitset bs(0xffffffff);
⑥、位图优缺点及应用:
优点:节省空间、效率高
缺点:只能处理整形
应用:
- 快速查找某个数据是否在一个集合中
- 排序 + 去重
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
⑦、完整代码及测试
#pragma once
#include<iostream>
#include<vector>namespace mz
{class bitset{public:bitset(size_t N){//N代表要开多少比特位(简称:位)_bits.resize(N / 32 + 1, 0);_num = N;}void set(size_t x){//把第x位设置为1,表示此位置存在size_t index = x / 32; //算出映射的位置在第几个整数size_t pos = x % 32; //算出x在整数的第几个位_bits[index] |= (1 << pos); //对于这个整数第pos的位置或1//1<<pos表示先把1移动到和pos相同位置的比特位上,因为pos=几,1就会左移几位//|=表示是或,即除了pos位置的位要变成1,++_num;}void reset(size_t x){//把第x位设置为0,表示此位置不存在size_t index = x / 32; //算出映射的位置在第几个整数size_t pos = x % 32; //算出x在整数的第几个位_bits[index] &= ~(1 << pos); //对于这个整数第pos的位置与0--_num;}//判断x在不在(也就是说x映射的位是否为1)bool test(size_t x){size_t index = x / 32; //算出映射的位置在第几个整数size_t pos = x % 32; //算出x在整数的第几个位return _bits[index] & (1 << pos); //结果非0为真,0则为假}private://int* _bits;std::vector<int> _bits;size_t _num; //表示存了多少个比特位,映射存储的多少个数据};void test_bitset(){bitset bs(100);bs.set(99);bs.set(98);bs.set(97);bs.reset(98);for (size_t i = 0; i < 100; ++i){printf("[%d]:%d\n", i, bs.test(i));}}}部分测试结果如下:

二、布隆过滤器
1、布隆过滤器的提出
我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉 那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用 户看过的所有历史记录,当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选,过滤掉那 些已经存在的记录。 如何快速查找呢?
- 1. 用哈希表存储用户记录,缺点:浪费空间
- 2. 用位图存储用户记录,缺点:位图一般只能处理整形,如果内容编号是字符串,就无法处理了
- 3. 将哈希与位图结合,即布隆过滤器
布隆过滤器是 由布隆( Burton Howard Bloom )在 1970 年提出的 一种紧凑型的、比较巧妙的 概 率型数据结构 ,特点是 高效地插入和查询,可以用来告诉你 “ 某样东西一定不存在或者可能存 在 ” ,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式 不仅可以提升查询效率,也 可以节省大量的内存空间 。
2、布隆过滤器的实现
①、基本结构
一般布隆过滤器存的是字符串或结构体等,一般不会是整形,因为整形就用位图来存了
布隆过滤器底层就是用位图实现的,因为字符串比较常用,故我们直接把字符串作为默认模板参数,其他三个Hash模板参数表示的是用三个位置来映射一个值
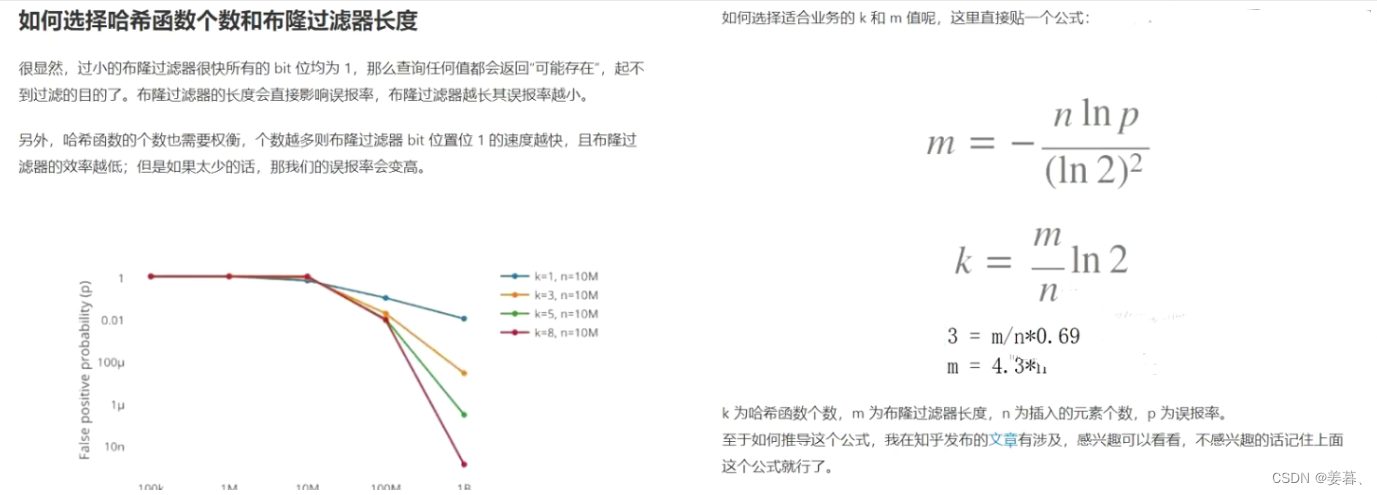
构造函数开多少个空间?
有大佬已经计算过了,10个元素就需要长度为43位,那我们干脆初始开个5倍
template<class K = string, class Hash1 = HashStr1, class Hash2 = HashStr2, class Hash3 = HashStr3>
class bloomfilter
{
public://直接上来开满会有问题,因为可能我本身可能就没映射几个值//那就根据你大概会存多少个数据,来对应开空间//到底开多少比较好有人算过,即你存多少个值就要映射到多少个位bloomfilter(size_t num):_bs(5 * num),_N(5 * num){}private:bitset _bs; //底层是一个位图size_t _N;
};②、三个Hash仿函数实现
因为要用三个映射位置来映射一个值,故要写三个字符串转为整形的函数,而又因为string类型比较常用,这三个仿函数会作为默认模板参数
下面是能降低哈希冲突的字符串算法(我们下面三个仿函数就选用下面三个算法):
struct HashStr1
{size_t operator()(const string& str){ //运用BKDRHashsize_t hash = 0;for (size_t i = 0; i < str.size(); ++i){hash *= 131;hash += str[i];}return hash;}
};struct HashStr2
{size_t operator()(const string& str){ //运用RSHashsize_t hash = 0;size_t magic = 63689; //魔数for (size_t i = 0; i < str.size(); ++i){hash *= magic;hash += str[i];magic *= 378551;}return hash;}
};struct HashStr3
{size_t operator()(const string& str){ //运用SDBMHashsize_t hash = 0;for (size_t i = 0; i < str.size(); ++i){hash *= 65599;hash += str[i];}return hash;}
};③、 set
函数是想把key这个数标志为存在,而我们说了要用三个位置来映射这个key值,则调用Hash仿函数先计算出字符串的映射位置,%_N是因为我们刚开始给位图就开了_N个比特位,你算出的映射位置很可能大于_N,故都%_N,既能存储也能统一,则一个key值就能用三个映射位置来表示了
注:Hash1是仿函数类型,Hash1()是仿函数对象,当然你也可以写为Hash1 hs1; hs1(key) % _N;但是明显更麻烦
void set(const K& key)
{size_t index1 = Hash1()(key) % _N;//利用Hash1类型的匿名对象size_t index2 = Hash2()(key) % _N;size_t index3 = Hash3()(key) % _N;_bs.set(index1);//表示index1这个位置存在_bs.set(index2);_bs.set(index3);
}④、 test
功能:判断key值存不存在
因为一个值用了三个映射位置,故我们判断计算出key的三个映射位置在位图中是否同时存在,同时存在key值才存在,反之有一个不存在就肯定不存在
bool test(const K& key)
{size_t index1 = Hash1()(key) % _N;if (_bs.test(index1) == false)return false;size_t index2 = Hash2()(key) % _N;if (_bs.test(index2) == false)return false;size_t index3 = Hash3()(key) % _N;if (_bs.test(index3) == false)return false;return true; //但这里也不一定是真的在,还是可能存在误判//判断在,是不准确的,可能存在误判//判断不在,是准确的
}⑤、 删除
布隆过滤器不能直接支持删除工作,因为在删除一个元素时,可能会影响其他元素。
一种支持删除的方法:将布隆过滤器中的每个比特位扩展成一个小的计数器,插入元素时给 k个计 数器 (k 个哈希函数计算出的哈希地址 ) 加一,删除元素时,给 k个计数器减一,通过多占用几倍存储 空间的代价来增加删除操作。缺陷:1. 无法确认元素是否真正在布隆过滤器中2. 存在计数回绕

void reset(const K& key)
{//将映射的位置给置0就可以?//不支持删除,可能会存在误删,故布隆过滤器一般不支持删除
}⑥、完整代码及测试
#pragma once
#include"bitset.h"
#include<string>using std::string;
using std::cout;
using std::endl;namespace mz
{struct HashStr1{size_t operator()(const string& str){ //运用BKDRHashsize_t hash = 0;for (size_t i = 0; i < str.size(); ++i){hash *= 131;hash += str[i];}return hash;}};struct HashStr2{size_t operator()(const string& str){ //运用RSHashsize_t hash = 0;size_t magic = 63689; //魔数for (size_t i = 0; i < str.size(); ++i){hash *= magic;hash += str[i];magic *= 378551;}return hash;}};struct HashStr3{size_t operator()(const string& str){ //运用SDBMHashsize_t hash = 0;for (size_t i = 0; i < str.size(); ++i){hash *= 65599;hash += str[i];}return hash;}};template<class K = string, class Hash1 = HashStr1, class Hash2 = HashStr2, class Hash3 = HashStr3>class bloomfilter{public://直接上来开满会有问题,因为可能我本身可能就没映射几个值//那就根据你大概会存多少个数据,来对应开空间//到底开多少比较好有人算过,即你存多少个值就要映射到多少个位bloomfilter(size_t num):_bs(5 * num),_N(5 * num){}void set(const K& key){size_t index1 = Hash1()(key) % _N;//利用Hash1类型的匿名对象size_t index2 = Hash2()(key) % _N;size_t index3 = Hash3()(key) % _N;_bs.set(index1);_bs.set(index2);_bs.set(index3);}bool test(const K& key){size_t index1 = Hash1()(key) % _N;if (_bs.test(index1) == false)return false;size_t index2 = Hash2()(key) % _N;if (_bs.test(index2) == false)return false;size_t index3 = Hash3()(key) % _N;if (_bs.test(index3) == false)return false;return true; //但这里也不一定是真的在,还是可能存在误判//判断在,是不准确的,可能存在误判//判断不在,是准确的}void reset(const K& key){//将映射的位置给置0就可以?//不支持删除,可能会存在误删,故布隆过滤器一般不支持删除}private:bitset _bs; //底层是一个位图size_t _N;};void test_bloomfilter(){bloomfilter<string> bf(100); //这里不给string,直接用<>也行,因为string是默认的bf.set("abcd");bf.set("aadd");bf.set("bcad");cout << bf.test("abcd") << endl;cout << bf.test("aadd") << endl;cout << bf.test("bcad") << endl;cout << bf.test("cbad") << endl;}
}
⑦、 优缺点
布隆过滤器优点
- 1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无
- 关
- 2. 哈希函数相互之间没有关系,方便硬件并行运算
- 3. 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
- 4. 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
- 5. 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
- 6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
布隆过滤器缺陷
- 1. 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再
- 建立一个白名单,存储可能会误判的数据)
- 2. 不能获取元素本身
- 3. 一般情况下不能从布隆过滤器中删除元素
- 4. 如果采用计数方式删除,可能会存在计数回绕问题
相关文章:

【C++和数据结构】位图和布隆过滤器
目录 一、位图 1、位图的概念 2、位图的实现 ①、基本结构 ②、set ③、reset: ④、test ⑤、问题: ⑥、位图优缺点及应用: ⑦、完整代码及测试 二、布隆过滤器 1、布隆过滤器的提出 2、布隆过滤器的实现 ①、基本结构 ②…...

Mybatis分页
本文主要讲解Mybatis分页相关的技术分享,如果觉得不错的话,就点个赞吧。。。。 Mybatis分页主要有2种类型: 一、物理分页: 1、定义: 物理分页是在数据库层面进行的分页,即通过SQL语句直接从数据库中查询…...
手写SVG图片
有时候QT中可能会需要一些简单的SVG图片,但是网上的质量参差不齐,想要满意的SVG图片,我们可以尝试直接手写的方法. 新建文本文档,将以下代码复制进去,修改后缀名为.svg,保存 <?xml version"1.0" encoding"utf-8"?> <svg xmlns"http://www…...
LVS负载均衡及LVS-NAT模式
一、集群概述 1.1 集群的背景 集群定义:为解决某个特定问题将多个计算机组合起来形成一个单系统 集群目的:为了解决系统的性能瓶颈 集群发展历史: 垂直扩展:向上扩展,增加单个机器的性能,即升级硬件 水…...

【Java集合类面试八】、 介绍一下HashMap底层的实现原理
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官: 介绍一下HashMap底层的…...
linux 安装操作 redis
1、redis概述和安装 1.1、安装redis 1. 下载redis 地址 https://download.redis.io/releases/ 2. 将 redis 安装包拷贝到 /opt/ 目录 3. 解压 tar -zvxf redis-6.2.1.tar.gz4. 安装gcc yum install gcc5. 进入目录 cd redis-6.2.16. 编译 make7. 执行 make install 进…...
博客后台模块续更(五)
十一、后台模块-菜单列表 菜单指的是权限菜单,也就是一堆权限字符串 1. 查询菜单 1.1 接口分析 需要展示菜单列表,不需要分页。可以针对菜单名进行模糊查询。也可以针对菜单的状态进行查询。菜单要按照父菜单id和orderNum进行排序 请求方式 请求路径…...

手写一个PrattParser基本运算解析器4: 简述iOS的编译过程
点击查看 基于Swift的PrattParser项目 iOS项目的编译过程与PrattParser解析器 前面三篇我们看到了PrattParser解析器的工作原理, 工作过程, 我们了解到PrattParser解析器实际上是模拟了编译过程中的 词法分析 、语法分析 、语义分析 、 中间代码生成 这几个编译前端过程. 那么P…...

【Java集合类面试六】、 HashMap有什么特点?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:HashMap有什么特点&…...
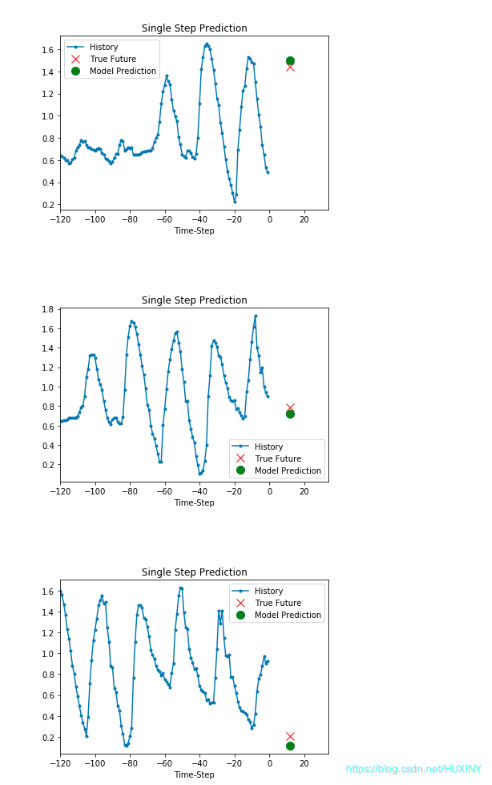
基于LSTM的天气预测 - 时间序列预测 计算机竞赛
0 前言 🔥 优质竞赛项目系列,今天要分享的是 机器学习大数据分析项目 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/po…...
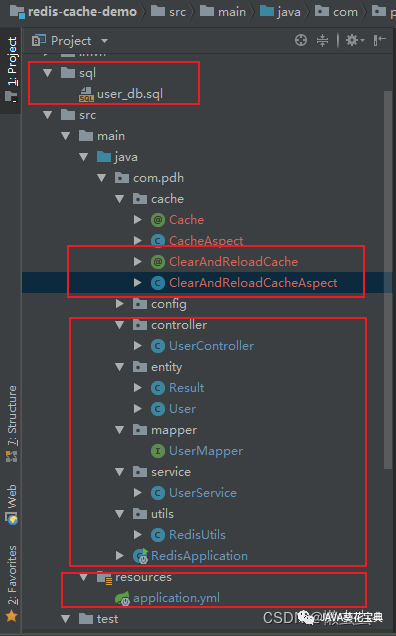
SpringBoot AOP + Redis 延时双删功能实战
一、业务场景 在多线程并发情况下,假设有两个数据库修改请求,为保证数据库与redis的数据一致性,修改请求的实现中需要修改数据库后,级联修改Redis中的数据。 请求一:A修改数据库数据 B修改Redis数据 请求二ÿ…...

【Java集合类面试七】、 JDK7和JDK8中的HashMap有什么区别?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:JDK7和JDK8中的HashMap有…...

el-tree 获取过滤后的树结构
正常来说element框架应该返回的,但实际上没有,只能自己处理了 递归处理,思路就是赋值,如果是自己过滤到的数据就push进去,不是就不要 let newCheckTree [] let tree get_tree(treeData,newCheckTree); //获取过滤…...

Windows连接SFTP服务
最近有个新需求需要通过SFTP方式连接到一个FTP中下载相关内容 1.使用命令行方式 在cmd中使用如下命令 sftp -P [port] [username]ip #示例 sftp -P 666 ftp123.123.123.123然后弹出的提示输入yes,再输入密码就可以了。 2.使用资源管理器方式 普通FTP可以使用资源…...
《红蓝攻防对抗实战》五.内网探测协议出网之DNS协议探测出网
DNS(Domain Name System)即域名解析系统,可将域名解析到对应访问IP。下面我们还是以系统自带命令为案例,进行演示DNS协议探测出网。 目录 一.Windows系统探测DNS协议出网 二.Linux系统探测DNS协议出网 1. Dig命令 2.Nslookup命…...

计算机算法分析与设计(18)---回溯法(介绍、子集和问题C++代码)
文章目录 一、回溯法介绍二、子集和问题2.1 知识概述2.2 代码编写 一、回溯法介绍 1. 回溯法(back tracking)是一种选优搜索法,又称为试探法,有“通用的解题法”之称,按选优条件向前搜索,以达到目标。但当探…...
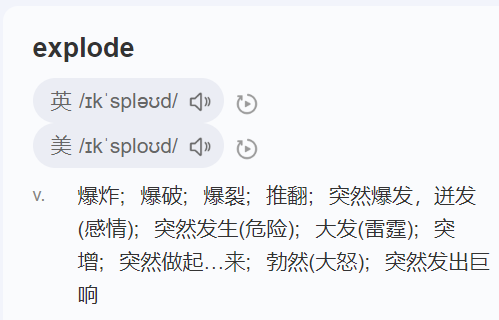
[Hive] explode
在 Hive 中,explode 函数用于将数组(Array)或者Map类型的列拆分成多行, 每个元素或键值对为一行。这允许我们在查询中对数组或 Map 进行扁平化操作。 下面是使用 explode 函数的示例: 假设我们有一个包含数组字段的表…...

2023年10月22日找工作面试交流遇到的基本问题
交叉编译解决的痛点问题 不同硬件体系结构之间的编译问题。嵌入式系统开发需要在主机上编写代码。提高效率和节省时间。软件移植和管理依赖关系。 不同硬件体系结构之间的编译问题:例如,你开发了一个针对Intel x86架构的应用程序,但想要在Ra…...

如何判断要不要用振动技术来进行设备预测性维护
在现代工业设备运行过程中,及时发现设备故障并进行维修对于确保生产线的正常运行至关重要。振动分析技术作为一种先进的设备监测和预测性维护方法,通过实时监测和分析设备的振动信号,可以提前发现潜在故障,降低停机时间和维护成本…...

数据结构和算法——用C语言实现所有树形结构及相关算法
文章目录 前言树和森林基础概念二叉树二叉树的遍历二叉树的构造树和森林与二叉树之间的转化树和森林的遍历 满二叉树完全二叉树线索二叉树线索二叉树的构造寻找前驱和后继线索二叉树的遍历 最优二叉树(哈夫曼树)哈夫曼树的构造哈夫曼编码 二叉排序树&…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...