当前位置： 首页 > news >正文

一起Talk Android吧（第五百零五回：如何调整组件在约束布局中的大小)

news 2025/12/16 2:36:20

文章目录

  • 背景介绍
  • 调整方法

各位看官们大家好，上一回中咱们说的例子是"如何调整组件在约束布局中的位置",这一回中咱们说的例子是" 如何调整组件在约束布局中的大小"。闲话休提，言归正转， 让我们一起Talk Android吧！

背景介绍

在使用约束(constraintlayout)布局的时候需要调整组件在布局中的大小，也就是长度和宽度。常用的做法是把width和height属性赋值为wrap_content,这样可以让组件依据自身的大小和约束条件来调整长度和宽度。不过这样调整出长度和宽度不够精确，而且不能适应不同大小的屏幕。接下来我们将介绍一种更好的调整方法。

调整方法

使用宽度和长度的percent属性可以精准调整组件的大小。

  • 首先把组件的长度和宽度属性值设置为0dp;
  • 然后调整长度和宽度的default属性值为percent，这表示通过百分比数值来控制组件的长度和宽度;
  • 最后就是给percent属性赋值了，值的范围在0-1之间。

这样可以精确地调整组件的长度和宽度。而且还可以适配不同大小的屏幕。此外，还有最大和最小属性，用来控制组件长度和宽度的最大值最小值。下面是详细的代码，请大家参考：

<TextV

相关文章：

一起Talk Android吧（第五百零五回：如何调整组件在约束布局中的大小)

文章目录 背景介绍调整方法各位看官们大家好，上一回中咱们说的例子是"如何调整组件在约束布局中的位置",这一回中咱们说的例子是" 如何调整组件在约束布局中的大小"。闲话休提，言归正转， 让我们一起Talk Android吧！ 背景介绍 在使用约束(constraintl…...

编程日记 2023/2/26 6:44:48

【数据库】数据库的完整性

第五章 数据库完整性 数据库完整性 数据库的完整性是指数据的正确性和相容性 数据的正确性是指数据是符合现实世界语义&#xff0c;反映当前实际状况的数据的相容性是指数据库的同一对象在不同的关系中的数据是符合逻辑的 关系模型中有三类完整性约束&#xff1a;实体完整性…...

编程日记 2023/2/26 6:42:24

基因净化车间装修设计方案SICOLAB

基因净化车间的设计方案应该根据实际需求进行定制&#xff0c;以下是一些规划建设要点和洁净设计要注意的事项&#xff1a;一、净化车间规划建设要点&#xff1a;&#xff08;1&#xff09;基因车间的面积应该根据实验项目的规模进行规划&#xff0c;包括充足的操作区域和足够的…...

编程日记 2023/2/26 6:41:16

java 内部类的四种“写法”

基本介绍语法格式分类成员内部类静态内部类局部内部类匿名内部类&#xff08;&#x1f402;&#x1f58a;&#xff09;一、基本介绍 : 1.概述当一个类的内部又完整地嵌套了另一个类时&#xff0c;被嵌套于内部的“内核”我们称之为“内部类”(inner class)&#xff1b;而包含该…...

编程日记 2023/2/26 6:40:06

【python】main方法教程

嗨害大家好鸭&#xff01; 我是小熊猫~ 首先 if name "main": 可以看成是python程序的入口&#xff0c; 就像java中的main&#xff08;&#xff09;方法&#xff0c; 但不完全正确。 事实上python程序是从上而下逐行运行的&#xff0c; 在.py文件中&#xff0c; 除…...

编程日记 2023/2/26 6:38:51

公司对不同职级能力抽象要求的具体化

要先把当前级别要求的能力提升到精通&#xff0c;然后尝试做下一级别的事情。 但可能不确定高一级的能力要求究竟怎样&#xff0c;不同Title&#xff0c;如“工程师”“高级工程师”和“资深工程师”等。但这样 Title 对我们理解不同级别的能力要求&#xff0c;完全无用。“高…...

编程日记 2023/2/26 6:37:35

Java之MinIO存储桶和对象API使用

环境搭建 创建一个 maven项目&#xff0c;引入依赖&#xff1a; <!-- minio依赖--><dependency><groupId>io.minio</groupId><artifactId>minio</artifactId><version>8.3.3</version></dependency><!-- 官方 minio…...

编程日记 2023/2/26 6:36:26

如何用java实现同时进行多个请求，可以将它们并行执行，从而减少总共的请求时间。

1.使用线程池 通过使用Java提供的线程池&#xff0c;可以将多个请求分配到不同的线程中并行执行。可以通过创建固定数量的线程池&#xff0c;然后将请求分配给线程池来实现。线程池会自动管理线程的数量和复用&#xff0c;从而减少了线程创建和销毁的开销&#xff0c;提高了程序…...

编程日记 2023/2/26 6:34:58

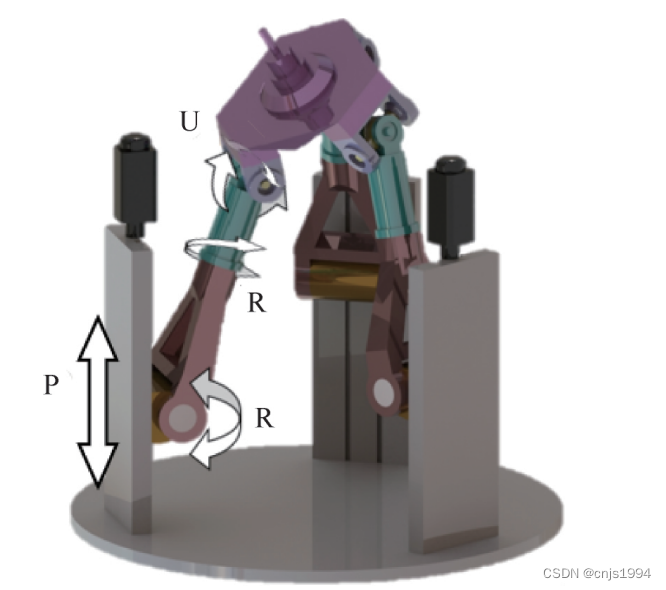
高端装备的AC主轴头结构

加工机器人的AC主轴头和位置相关动力学特性1. 位置依赖动态特性及其复杂性2. AC主轴头2.1 常见主轴头摆角结构2.2 摆动机构3. 加装AC主轴头的作用和局限性4. 切削机器人的减速器类型5. 其他并联结构形式参考文献资料1. 位置依赖动态特性及其复杂性 However, FRF measurements …...

编程日记 2023/2/26 6:33:40

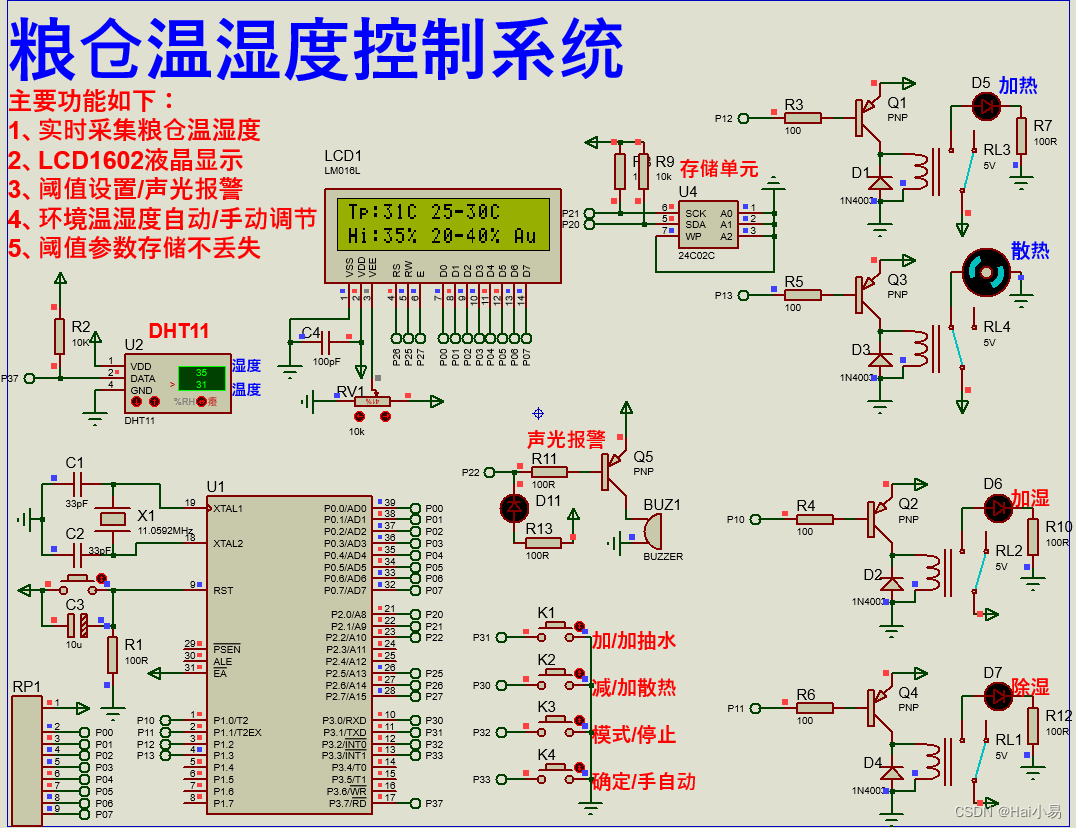
【Proteus仿真】【51单片机】粮仓温湿度控制系统设计

文章目录一、功能简介二、软件设计三、实验现象联系作者一、功能简介 本项目使用Proteus8仿真51单片机控制器&#xff0c;使用声光报警模块、LCD1602显示模块、DHT11温湿度模块、继电器模块、加热加湿除湿风扇等。 主要功能&#xff1a; 系统运行后&#xff0c;LCD1602显示传…...

编程日记 2023/2/26 6:32:02

【LINUX】环境变量以及main函数的参数

文章目录前言环境变量常见环境变量&#xff1a;设置环境变量&#xff1a;和环境变量相关的命令&#xff1a;环境变量的组织方式&#xff1a;获取环境变量环境变量可以被子进程继承环境变量总结main函数的参数前言 大家好久不见&#xff0c;今天分享的内容是环境变量和main函数…...

编程日记 2023/2/26 6:30:42

使用Pyparsing为嵌入式开发定义自己的脚本语言

Python在嵌入式开发中也很流行生成实用脚本。Pyparsing还允许你轻松地定义在Python上下文中运行的定制脚本语言。Python实现的系统旨在能够独立执行用户传递的一系列命令。你希望系统以脚本的形式接收命令。用户应该能够定义条件。这种对通信中逻辑元素的最初简单的声音要求&am…...

编程日记 2023/2/26 6:28:52

C win32基础学习（二）

上一篇我们已经介绍了关于窗口程序的一些基本知识。从本篇开始我们将正式进入C win32的学习中去。 正文 窗口创建过程 定义WinMain函数 定义窗口处理函数(自定义&#xff0c;处理消息) 注册窗口类&#xff08;向操作系统写入一些数据&#xff09; 创建窗口&#xff08;内存…...

编程日记 2023/2/26 6:27:37

理论五：控制反转、依赖反转、依赖注入，这三者有何区别和联系？

关于SOLID原则,我们已经学过单一职责、开闭、里式替换、接口隔离这四个原则。今天,我们再来学习最后一个原则:依赖反转原则。在前面几节课中,我们讲到,单一职责原则和开闭原则的原理比较简单,但是,想要在实践中用好却比较难。而今天我们要讲到的依赖反转原则正好相反。这个原则…...

编程日记 2023/2/26 6:26:11

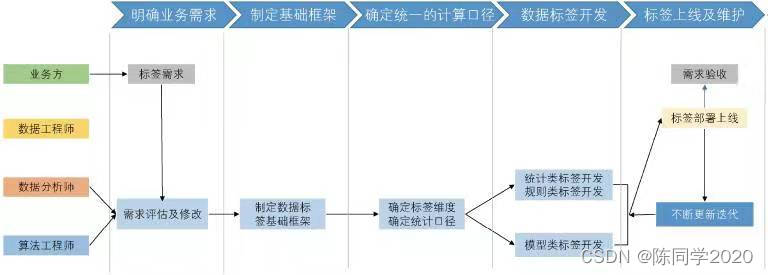
读书笔记//《数据分析之道》

出版时间&#xff1a;2022年 作者曾在互联网大厂做数据分析。从举例可以洞见作者的工作经历。 点评&#xff1a;作者在数据分析领域非常资深&#xff0c;尝试在书中提供一个数据分析工作框架参考。书本内容有点感觉是ppt的集合&#xff0c;辅以案例说明。不过&#xff0c;干货还…...

编程日记 2023/2/26 6:23:26

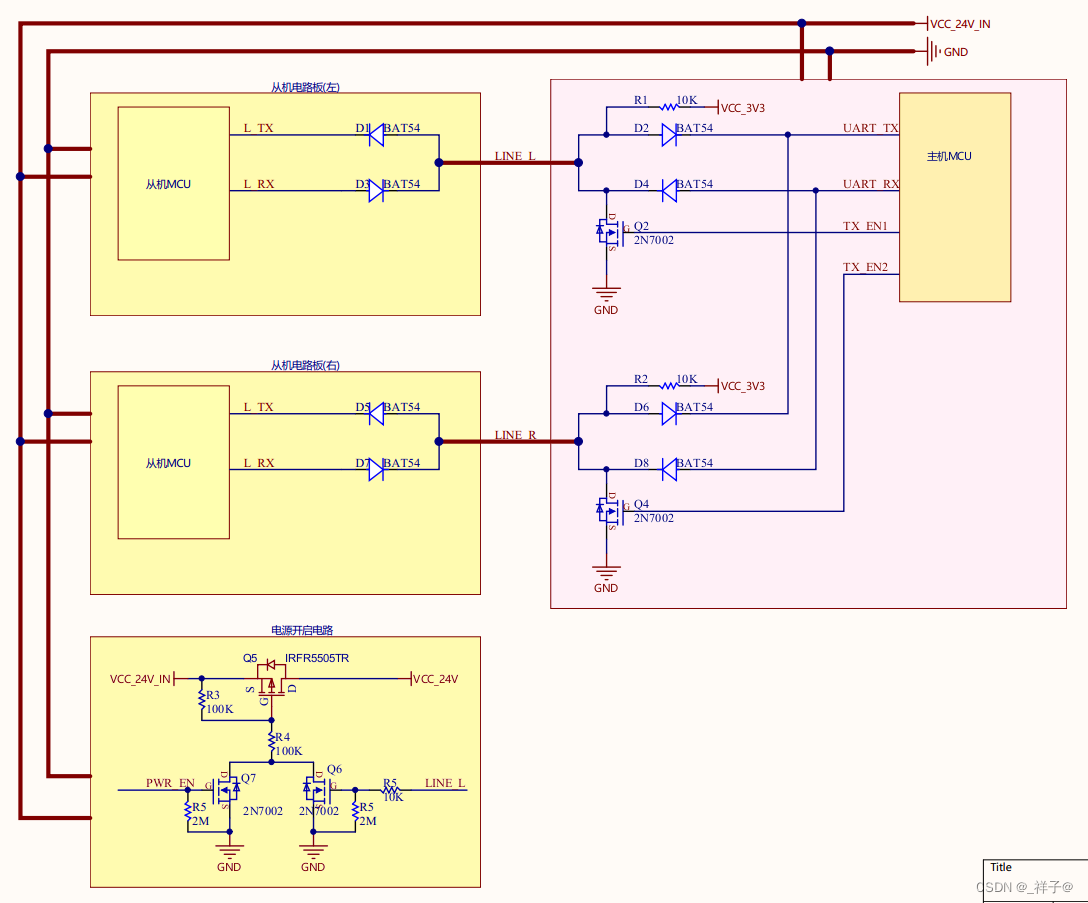
1个串口用1根线实现多机半双工通信+开机控制电路

功能需求&#xff1a; 主机使用一个串口&#xff0c;与两个从机进行双向通信&#xff0c;主机向从机发送数据&#xff0c;从机能够返回数据&#xff0c;由于结构限制&#xff0c;主机与从机之间只有3根线&#xff08;电源、地、数据线&#xff09;&#xff0c;并且从机上没有设…...

编程日记 2023/2/26 6:22:00

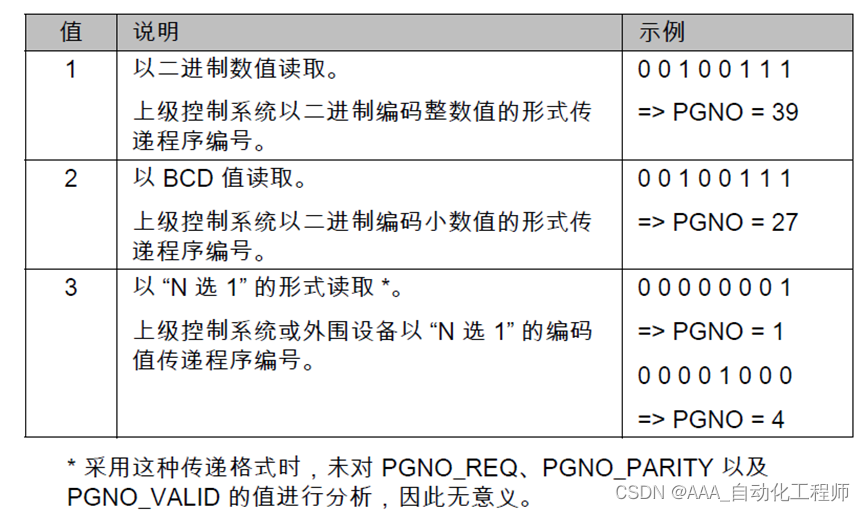
KUKA机器人外部自动运行模式的相关信号配置

KUKA机器人外部自动运行模式的相关信号配置 通过例如PLC这样的控制器来进行外部自动运行控制时，运行接口向机器人控制系统发出机器人进程的相关信号（例如运行许可、故障确认、程序启动等），机器人向上级控制系统发送有关运行状态和故障状态的信息。 必需的配置：  配置CEL…...

编程日记 2023/2/26 6:20:28

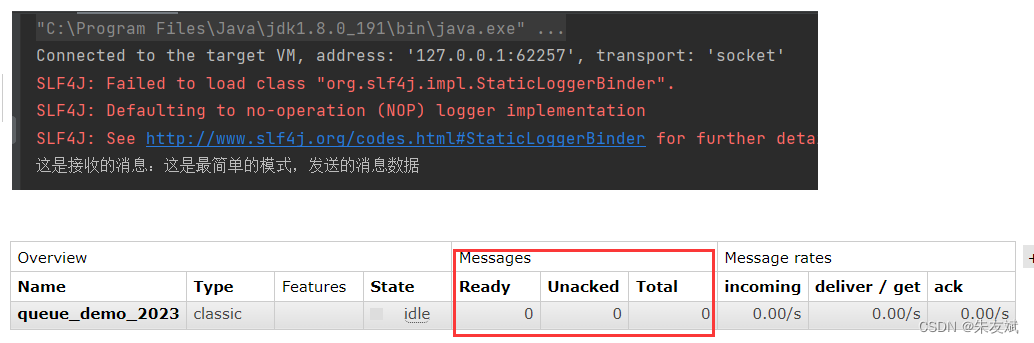
【RabbitMQ笔记02】消息队列RabbitMQ七种模式之最简单的模式

这篇文章&#xff0c;主要介绍RabbitMQ消息队列中七种模式里面最简单的使用模式。 目录 一、消息队列的使用 1.1、消息队列七种模式 1.2、最简单的模式使用 &#xff08;1&#xff09;引入依赖 &#xff08;2&#xff09;编写生产者 &#xff08;3&#xff09;编写消费者…...

编程日记 2023/2/26 6:19:04

Spring MVC 源码- RequestToViewNameTranslator 组件

RequestToViewNameTranslator 组件RequestToViewNameTranslator 组件&#xff0c;视图名称转换器&#xff0c;用于解析出请求的默认视图名。就是说当 ModelAndView 对象不为 null&#xff0c;但是它的 View 对象为 null&#xff0c;则需要通过 RequestToViewNameTranslator 组件…...

编程日记 2023/2/26 6:17:51

Linux--TCP编程--0216 17

观前提示&#xff1a;本篇博文的一些接口需要前几篇博文实现的 线程池的实现Liunx--线程池的实现--0208 09_Gosolo&#xff01;的博客-CSDN博客 线程池的单例模式Linux--线程安全的单例模式--自旋锁--0211_Gosolo&#xff01;的博客-CSDN博客 1.TCP编程需要用的接口 创建 sock…...

编程日记 2023/2/26 6:16:27

在软件开发中正确使用MySQL日期时间类型的深度解析

在日常软件开发场景中&#xff0c;时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志&#xff0c;到供应链系统的物流节点时间戳&#xff0c;时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库&#xff0c;其日期时间类型的…...

编程新知 2025/10/16 13:22:06

Android Wi-Fi 连接失败日志分析

1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分&#xff1a; 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析&#xff1a; CTR…...

编程新知 2025/9/14 19:44:52

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2025/7/5 11:03:11

Xshell远程连接Kali（默认 | 私钥）Note版

前言:xshell远程连接&#xff0c;私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

编程新知 2025/12/12 3:26:16

测试markdown--肇兴

day1&#xff1a; 1、去程&#xff1a;7:04 --11:32高铁 高铁右转上售票大厅2楼&#xff0c;穿过候车厅下一楼&#xff0c;上大巴车 &#xffe5;10/人 **2、到达&#xff1a;**12点多到达寨子&#xff0c;买门票&#xff0c;美团/抖音&#xff1a;&#xffe5;78人 3、中饭&a…...

编程新知 2025/12/14 11:45:02

postgresql|数据库|只读用户的创建和删除（备忘）

CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

编程新知 2025/9/18 19:34:22

跨链模式：多链互操作架构与性能扩展方案

跨链模式&#xff1a;多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈&#xff1a;模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展&#xff08;H2Cross架构&#xff09;&#xff1a; 适配层&#xf…...

编程新知 2025/12/13 5:40:35

【AI学习】三、AI算法中的向量

在人工智能&#xff08;AI&#xff09;算法中&#xff0c;向量&#xff08;Vector&#xff09;是一种将现实世界中的数据&#xff08;如图像、文本、音频等&#xff09;转化为计算机可处理的数值型特征表示的工具。它是连接人类认知&#xff08;如语义、视觉特征&#xff09;与…...

编程新知 2025/8/12 22:58:13

Redis数据倾斜问题解决

Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中&#xff0c;部分节点存储的数据量或访问量远高于其他节点&#xff0c;导致这些节点负载过高&#xff0c;影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

编程新知 2025/12/15 21:48:57

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数 在软件开发中，单例模式（Singleton Pattern）是一种常见的设计模式，确保一个类仅有一个实例，并提供一个全局访问点。在多线程环境下，实现单例模式时需要注意线程安全问题，以防止多个线程同时创建实例，导致…...

编程新知 2025/11/25 19:50:27