从头开始使用 KNN 进行 KNN 和 MNIST 手写数字识别的初学者指南

一、说明
MNIST (“修改后的国家标准与技术研究所”)是事实上的计算机视觉“hello world”数据集。自 1999 年发布以来,这个经典的手写图像数据集一直作为分类算法基准测试的基础。随着新的机器学习技术的出现,MNIST 仍然是研究人员和学习者的可靠资源。
最终目标是从数万张手写图像的数据集中正确识别数字。

图片来源:维基百科
我们现在将尝试从头开始使用KNN(K 最近邻)算法对数字进行分类。
在此之前,我们先来了解一下KNN到底是什么!
二、如何读取Mnist?
读取Mnist可以用tensorflow完成,也可以用numpy完成。如下:
def load_data(path):with np.load(path) as f:x_train, y_train = f['x_train'], f['y_train']x_test, y_test = f['x_test'], f['y_test']return (x_train, y_train), (x_test, y_test)(x_train, y_train), (x_test, y_test) = load_data('../input/mnist-numpy/mnist.npz')三、什么是KNN?
K 最近邻可用于分类和回归。K 最近邻是一种简单的算法,它存储所有可用案例并根据相似性度量对新案例进行分类。
KNN是一种基于实例的学习或惰性学习,其中函数仅在本地进行近似,并且所有计算都推迟到分类。KNN 算法是所有机器学习算法中最简单的算法之一。
它是一种非参数算法,不需要训练数据来进行推理,因此与参数学习算法相比,训练速度要快得多,而推理速度要慢得多,原因显而易见。
四、KNN 到底是如何工作的?
我们通过一个简单的例子来理解这个算法。
以下是红色圆圈 (RC)和绿色方块 (GS)的分布:

您打算找出蓝星 (BS) 的等级。BS 可以是 RC 或 GS,仅此而已。KNN 算法中的“K”是我们希望投票的最近邻居。假设 K = 3。因此,我们现在将以 BS 为中心制作一个圆,其大小仅包含平面上的三个数据点。更多详情请参考下图:
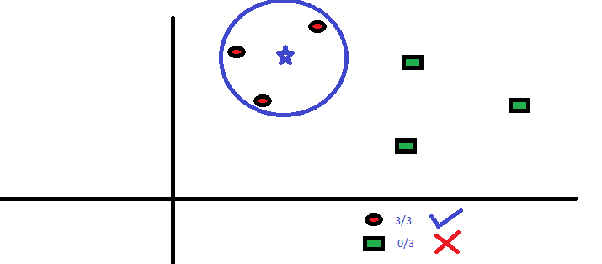
离SB最近的3个点都是RC。因此,根据我们的智能置信水平,我们可以说 bs 应该属于 RC 类别。在这里,选择变得非常明显,因为最近邻居的所有 3 票都投给了 RC。在此算法中,参数K的选择至关重要。接下来,我们将了解得出最有效的K需要考虑哪些因素。
注: KNN 的一些假设 —
- 当您有 2 个类时,请选择奇数 K 值以避免平局。即,如果新数据点位于两个类之间,则它无法决定选择哪一个。
- K 不能是类数的倍数
- 如果 K 非常小(过拟合),如果您有很多数据点 (n) 将不准确
- 如果 K 很大(Underfit),K 一定不能等于数据点的数量 n
五、我们如何选择因子K?
首先,让我们尝试了解 K 对算法到底有什么影响。如果我们看到最后一个例子,假设所有 6 个训练观察值保持不变,使用给定的 K 值,我们可以为每个类别划分边界。

正如您所看到的,训练样本在 K=1 时的错误率始终为零。这是因为与任何训练数据点最接近的点就是其本身。因此,当 K=1 时,预测总是准确的。如果验证误差曲线相似,我们选择的 K 将为 1。
以下是不同 K 值的验证误差曲线:

这让故事变得更加清晰。当 K=1 时,我们过度拟合了边界。因此,错误率最初下降并达到最小值。在最小值点之后,它会随着 K 的增加而增加。为了获得 K 的最佳值,您可以将训练和验证与初始数据集分开。现在绘制验证误差曲线以获得 K 的最佳值。这个 K 值应该用于所有预测,这与肘部方法类似。
六、KNN 的伪代码
任何人都可以按照下面给出的伪代码步骤来实现 KNN 模型。
- 加载数据
- 初始化k的值
- 要获得预测类别,请从 1 迭代到训练数据点总数
- 计算测试数据与每行训练数据之间的距离。在这里,我们将使用欧几里德距离作为距离度量,因为它是最流行的方法。其他可以使用的度量有切比雪夫、余弦等。
- 根据距离值对计算出的距离进行升序排序
- 从排序数组中获取前 k 行
- 获取这些行中最常见的类别
- 返回预测的类别
七、KNN 的变体
在传统提出的 KNN 中,正如我们所见,我们对所有类别和距离给予相同的权重,这是您应该了解的 KNN 的变体!
7.1 距离加权 KNN
在距离加权 KNN 中,您基本上更多地强调更接近测试值的值,更少地强调远离测试值的值,并类似地为每个值分配权重。

其中 wk 是 —
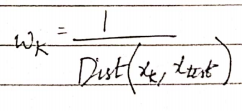
7.2 加权距离函数
由于我们在传统 KNN 中为所有特征赋予了相同的权重,因此我们尝试在此变体中为每个特征分配不同的权重。重要的特征将具有较大的权重,而不太重要的特征将具有较低的权重,而最不重要的特征将具有0或接近0的权重。

八、测量距离的方法
- 闵可夫斯基距离
- 曼哈顿距离
- 欧氏距离
- 汉明距离
- 余弦距离
当数据具有高维度时,曼哈顿距离通常优于更常见的欧几里得距离。汉明距离用于衡量分类变量之间的距离,余弦距离度量主要用于查找两个数据点之间的相似程度,明可夫斯基是欧几里德距离和曼哈顿距离在较低级别上的推广。
有关这方面的更多信息,请查看 —机器学习中使用的不同类型的距离度量。
九、从头开始实施
您最初需要导入的库:
import numpy as np
import operator
from operator import itemgetter让我们首先定义一个返回两点之间的欧几里得距离的函数:
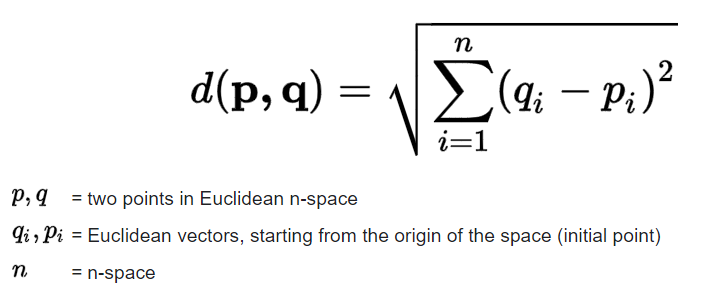
图片来源:Science Direct — 欧几里得距离公式
def euc_dist(x1, x2):return np.sqrt(np.sum((x1-x2)**2))现在,让我们编写一个类“KNN”并为“K”值初始化一个实例:
class KNN:def __init__(self, K=3):self.K = K让我们在类中添加另一个函数来初始化实例以拟合我们的训练集 — X-train 和 y-train:
class KNN:def __init__(self, K=3):self.K = Kdef fit(self, x_train, y_train):self.X_train = x_trainself.Y_train = y_train现在让我们将预测函数添加到此类中:
def predict(self, X_test):predictions = [] for i in range(len(X_test)):dist = np.array([euc_dist(X_test[i], x_t) for x_t in self.X_train])dist_sorted = dist.argsort()[:self.K]neigh_count = {}for idx in dist_sorted:if self.Y_train[idx] in neigh_count:neigh_count[self.Y_train[idx]] += 1else:neigh_count[self.Y_train[idx]] = 1sorted_neigh_count = sorted(neigh_count.items(), key=operator.itemgetter(1), reverse=True)predictions.append(sorted_neigh_count[0][0]) return predictions哇!这是很多代码!让我们逐行理解这一点——
我们初始化了一个列表来存储我们的预测,然后运行一个循环来计算每个测试示例到每个相应训练示例的欧几里德距离,并将所有这些距离存储在 NumPy 数组中,之后我们返回第一个 K- 的索引对距离值进行排序,然后我们创建了一个字典,其中类标签作为键,它们的出现作为每个键的值。
然后,我们将每个计数附加到每个键值对的 neigh_count 字典中,之后,我们将键值对从最常出现的值到最少出现的值进行排序,其中,我们最常出现的值将是我们对每个训练示例的预测。然后我们返回了预测。
这就是从头开始实现 KNN 的全部内容,现在让我们在 MNIST 数据集上测试我们的模型!
from sklearn.datasets import load_digits
mnist = load_digits()
print(mnist.data.shape)
Out:
(1797, 64)
X = mnist.data
y = mnist.target将我们的数据分为训练和测试:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=123)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
Out:
(1347, 64) (1347,)
(450, 64) (450,)
print(np.unique(y_train,return_counts=True))
print(np.unique(y_test,return_counts=True))
Out:
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), array([127, 140, 136, 143, 129, 134, 133, 138, 129, 138])) (array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), array([51, 42, 41, 40, 52, 48, 48, 41, 45, 42]))将数据分为测试和训练就足够了吗?真的有帮助吗?
通常建议使用交叉验证来分割我们的数据-
在交叉验证中,我们没有将数据拆分为两部分,而是将其拆分为 3 部分(或K取决于K 折交叉验证中的 K 值)。训练数据、交叉验证数据和测试数据。在这里,我们使用训练数据来查找最近邻居,我们使用交叉验证数据来找到“K”的最佳值(这里是 K 个邻居),最后我们在完全看不见的测试数据上测试我们的模型。这个测试数据就相当于未来未见过的数据点。
让我们导入更多辅助函数来评估 Sklearn 中的模型:
from sklearn.metrics import precision_recall_fscore_support
from sklearn.metrics import accuracy_score使用从 3 到 100 的所有可能的 K 值(奇数)训练我们的模型:
kVals = np.arange(3,100,2)
accuracies = []
for k in kVals:model = KNN(K = k)model.fit(X_train, y_train)pred = model.predict(X_test)acc = accuracy_score(y_test, pred)accuracies.append(acc)print("K = "+str(k)+"; Accuracy: "+str(acc))
Out:
K = 3; Accuracy: 0.9755555555555555
K = 5; Accuracy: 0.9755555555555555
K = 7; Accuracy: 0.9755555555555555
K = 9; Accuracy: 0.9755555555555555
K = 11; Accuracy: 0.9733333333333334
K = 13; Accuracy: 0.9711111111111111
K = 15; Accuracy: 0.9688888888888889
K = 17; Accuracy: 0.9666666666666667
K = 19; Accuracy: 0.9666666666666667
K = 21; Accuracy: 0.9666666666666667
K = 23; Accuracy: 0.9644444444444444
K = 25; Accuracy: 0.9644444444444444
K = 27; Accuracy: 0.9666666666666667
K = 29; Accuracy: 0.9622222222222222
K = 31; Accuracy: 0.96
K = 33; Accuracy: 0.96
K = 35; Accuracy: 0.9577777777777777
K = 37; Accuracy: 0.9577777777777777
K = 39; Accuracy: 0.9577777777777777
K = 41; Accuracy: 0.9555555555555556
K = 43; Accuracy: 0.9511111111111111
K = 45; Accuracy: 0.9488888888888889
K = 47; Accuracy: 0.9444444444444444
K = 49; Accuracy: 0.9444444444444444
K = 51; Accuracy: 0.9377777777777778
K = 53; Accuracy: 0.9355555555555556
K = 55; Accuracy: 0.9333333333333333
K = 57; Accuracy: 0.9333333333333333
K = 59; Accuracy: 0.9311111111111111
K = 61; Accuracy: 0.9333333333333333
K = 63; Accuracy: 0.9333333333333333
K = 65; Accuracy: 0.9311111111111111
K = 67; Accuracy: 0.9288888888888889
K = 69; Accuracy: 0.9266666666666666
K = 71; Accuracy: 0.9288888888888889
K = 73; Accuracy: 0.9311111111111111
K = 75; Accuracy: 0.9288888888888889
K = 77; Accuracy: 0.9266666666666666
K = 79; Accuracy: 0.92
K = 81; Accuracy: 0.9222222222222223
K = 83; Accuracy: 0.9222222222222223
K = 85; Accuracy: 0.92
K = 87; Accuracy: 0.9177777777777778
K = 89; Accuracy: 0.9177777777777778
K = 91; Accuracy: 0.9111111111111111
K = 93; Accuracy: 0.9111111111111111
K = 95; Accuracy: 0.9088888888888889
K = 97; Accuracy: 0.9088888888888889
K = 99; Accuracy: 0.9066666666666666该模型在 K=3 时最准确:
max_index = accuracies.index(max(accuracies))
print(max_index)
Out:
0绘制我们的准确性:
from matplotlib import pyplot as plt
plt.plot(kVals, accuracies)
plt.xlabel("K Value")
plt.ylabel("Accuracy")
Out:
Text(0, 0.5, 'Accuracy')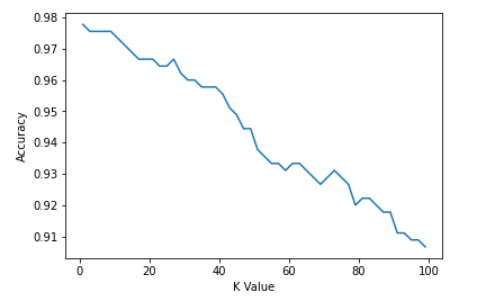
检查精确率、召回率和 F 分数(以获得最准确的 K 值):
model = KNN(K = 3)
model.fit(X_train, y_train)
pred = model.predict(X_train)
precision, recall, fscore, _ = precision_recall_fscore_support(y_train, pred)
print("Precision \n", precision)
print("\nRecall \n", recall)
print("\nF-score \n", fscore)
Out:
Precision [1. 0.9929078 1. 1. 1. 1.0.98518519 1. 0.9921875 0.99275362]Recall [1. 1. 1. 1. 1. 0.992537311. 0.99275362 0.98449612 0.99275362]F-score [1. 0.99644128 1. 1. 1. 0.996254680.99253731 0.99636364 0.98832685 0.99275362]在测试集上对经过训练的模型进行推理:
model = KNN(K = 3)
model.fit(X_train, y_train)
pred = model.predict(X_test)
acc = accuracy_score(y_test, pred)
precision, recall, fscore, _ = precision_recall_fscore_support(y_test, pred)
print("Precision \n", precision)
print("\nRecall \n", recall)
print("\nF-score \n", fscore)
Out:
Precision [1. 0.89361702 1. 0.93023256 0.98113208 1.1. 1. 1. 0.95 ]Recall [1. 1. 0.97560976 1. 1. 0.958333331. 1. 0.91111111 0.9047619 ]F-score [1. 0.94382022 0.98765432 0.96385542 0.99047619 0.97872341. 1. 0.95348837 0.92682927]
print(acc) #testing accuracy
Out:
0.9755555555555555 我知道一下子要吸收很多东西!但你坚持到了最后!对此表示敬意!不要忘记查看我即将发表的文章!
相关文章:

从头开始使用 KNN 进行 KNN 和 MNIST 手写数字识别的初学者指南
一、说明 MNIST (“修改后的国家标准与技术研究所”)是事实上的计算机视觉“hello world”数据集。自 1999 年发布以来,这个经典的手写图像数据集一直作为分类算法基准测试的基础。随着新的机器学习技术的出现,MNIST 仍然是研究人…...
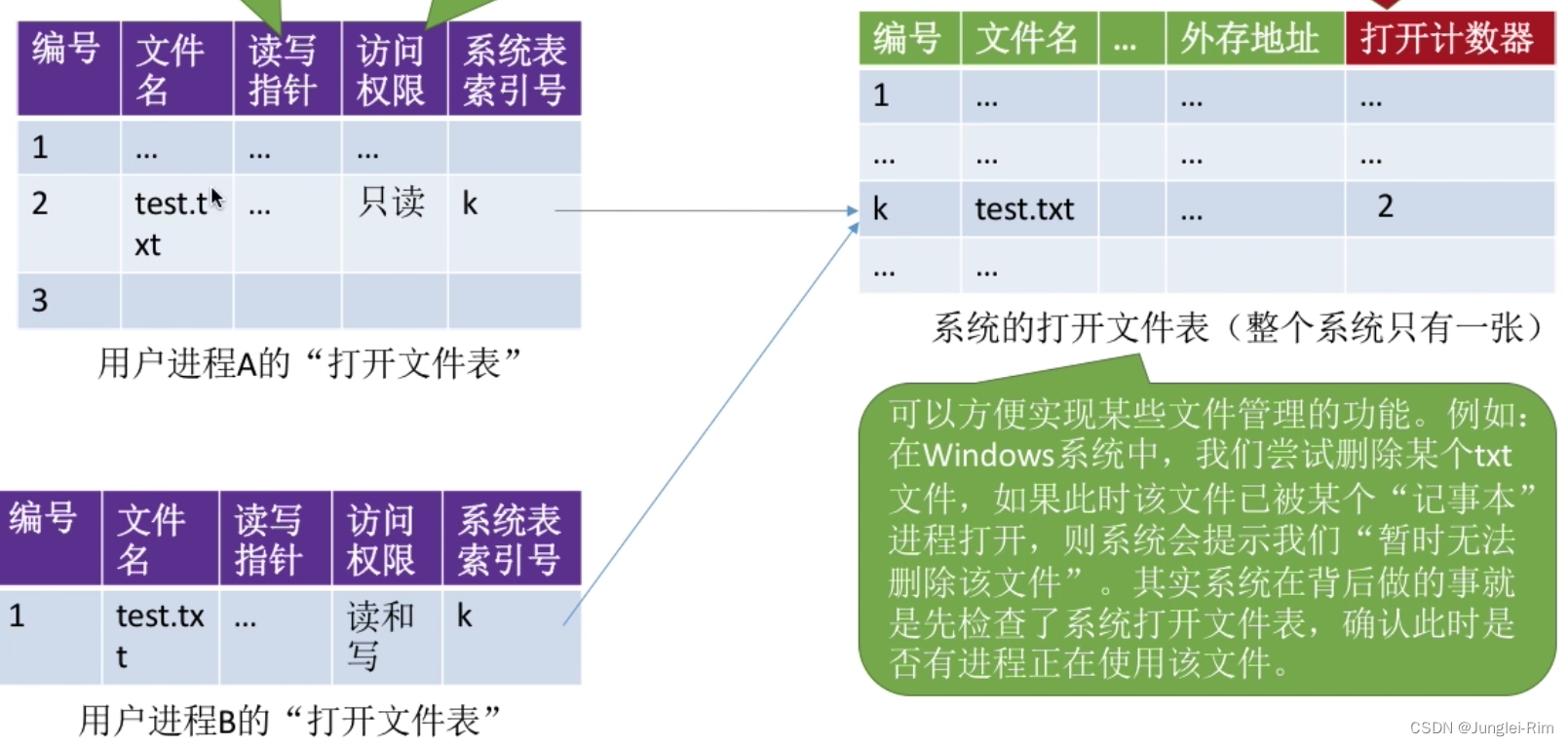
文件的基本操作(创建文件,删除文件,读写文件,打开文件,关闭文件)
1.创建文件(create系统调用) 1.进行Create系统调用时, 需要提供的几个主要参数: 1.所需的外存空间大小(如:一个盘块,即1KB) 2.文件存放路径(“D:/Demo”) 3.文件名(这个地方默认为“新建文本文档.txt”) …...

微积分(二) 导数与微分
前言 导数反映了函数值相对于自变量的变化快慢程度,而微分则表明当自变量有微小变化时,函数值大体上变化多少 瞬时速度的解决——极限 牛顿采用了一种无限逼近的方法。 平均速度的定义:如果一个物体在一段时间△t内位移了s,它在这段时间内的平均速度…...
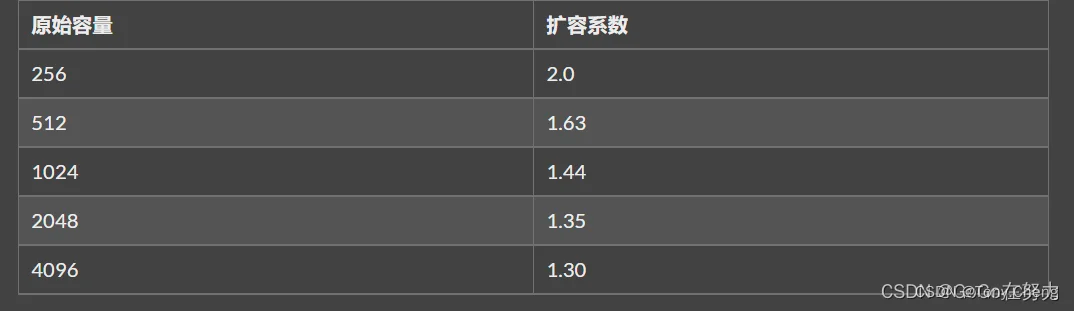
go语言Array 与 Slice
有的语言会把数组用作常用的基本的数据结构,比如 JavaScript,而 Golang 中的数组(Array),更倾向定位于一种底层的数据结构,记录的是一段连续的内存空间数据。但是在 Go 语言中平时直接用数组的时候不多,大多数场景下我…...

Ubuntu自启动设置
ubuntu中编写shell脚本开机自动启动(推荐)_Linux_脚本之家 1. vim test.sh 2. #!/bin/bash ### BEGIN INIT INFO # Provides: test # Required-Start: $remote_fs $syslog # Required-Stop: $remote_fs $syslog # Default-Start: 2 3 4 5 # Default-Stop: 0 1 6 …...

Qwen 通义千问 14B 模型,长文本问答效果测试
千问的config: seq_len2k max_position_embedding8k 注意,以下实验结果的字数是token数,不是中文字符数。 不使用动态ntk 12000字输入: 乱码5000字输入:乱码1500字输入:正常 不使用动态ntk,…...

Prefix-Tuning源码解析
Prefix-Tuning源码解析 Prefix-Tuning在PEFT包中的源码实现 改写自Based on https://github.com/THUDM/P-tuning-v2/blob/main/model/prefix_encoder.py import torch from transformers import PretrainedConfigclass PrefixEncoder(torch.nn.Module):rThe torch.nn model t…...
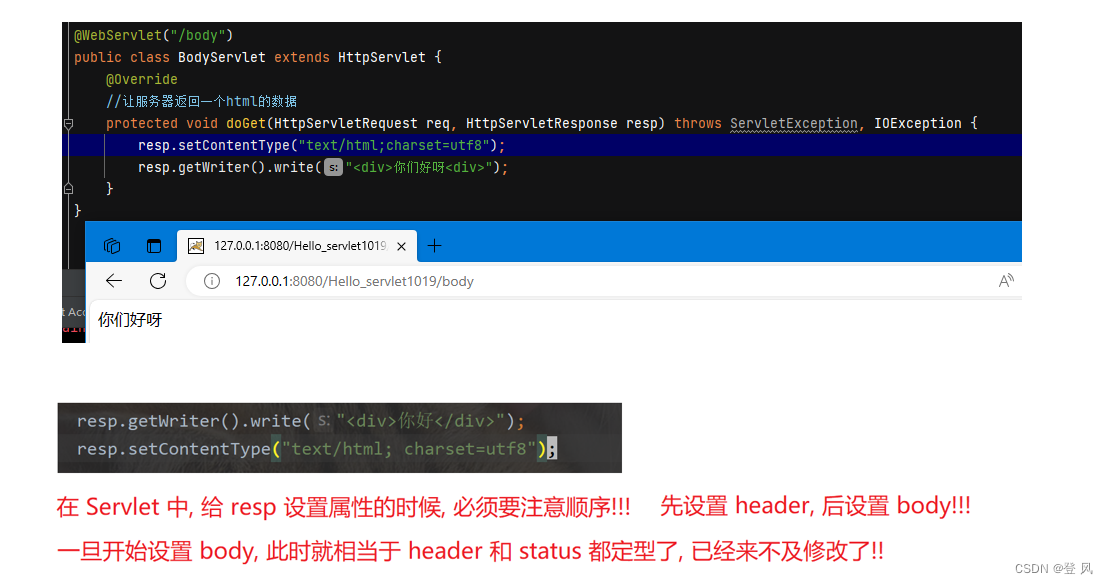
Java EE-servlet API 三种主要的类
上述的代码如下: import javax.servlet.ServletException; import javax.servlet.annotation.WebServlet; import javax.servlet.http.HttpServlet; import javax.servlet.http.HttpServletRequest; import javax.servlet.http.HttpServletResponse; import java.i…...

简单谈谈我参加数据分析省赛的感受与体会
数据分析省赛的感受与体会 概要考试前的感受与体会考试注意事项小结 概要 大数据分析省赛指的是在省级范围内举办的大数据分析竞赛活动。该竞赛旨在鼓励和推动大数据分析领域的技术创新和人才培养,促进大数据技术与应用的深度融合,切实解决实际问题。参…...
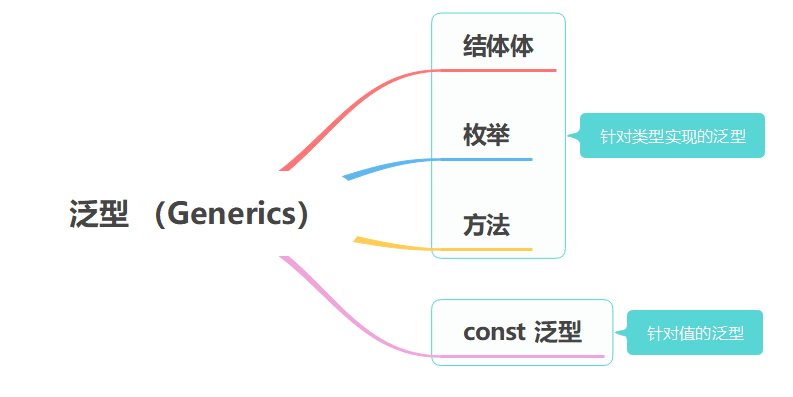
rust学习——泛型 (Generics)
文章目录 泛型 Generics泛型详解结构体中使用泛型枚举中使用泛型方法中使用泛型为具体的泛型类型实现方法 const 泛型(Rust 1.51 版本引入的重要特性)const 泛型表达式 泛型的性能 泛型 Generics Go 语言在 2022 年,就要正式引入泛型…...

【USRP】通信之有线通信
有线通信: 有线通信是指使用物理线路或媒体(例如,铜线、同轴电缆、光纤)进行数据、声音和视频传输的通信方式。由于它依赖于实体传输媒介,有线通信通常具有较高的稳定性和可靠性,并能支持长距离的高带宽通…...

【算法】BFS
BFS广度优先搜索 1. 概念理解 广度优先搜索(BFS)是指,以一个起点(原点、结点、根)为基本点,向其所要搜索的方向扩散,并最终到达目标点的搜索方法。 2. 应用方向 有迷宫问题、层序遍历等应用。 3. 迷宫问题 以迷宫问题为例。 当想要从左…...
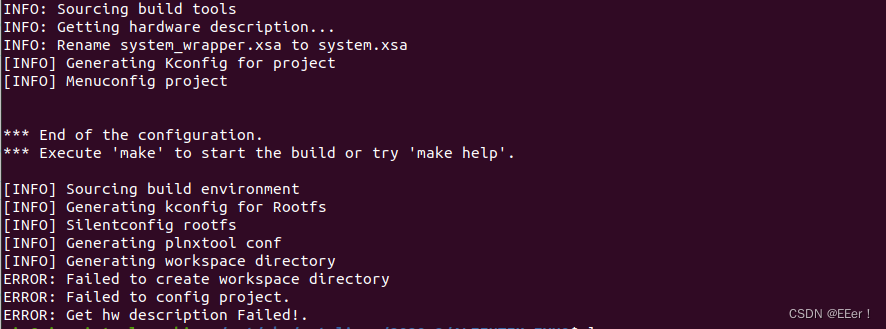
ZYNQ7020开发(二):zynq linux系统编译
文章目录 一、编译前准备二、SDK编译三、编译步骤总结四、问题汇总 一、编译前准备 1.设置环境变量 source /opt/pkg/petalinux/2020.2/settings.sh/opt/pkg/petalinux/2020.2是上一节petalinux的安装目录 2.创建 petalinux 工程 进入petalinux安装目录(例如:/op…...

Kafka 自动配置部署信息的脚本记录
自动配置 Kafka 整理服务器内容时,发现一个测试 Kafka 的的一个脚本,它可以自动部署 Kafka ,指定三个参数,完成 Kafka 的配置过程。 basePath$1 brokerId$2 zookeeperConnect$3 localIpifconfig |grep inet| awk {print $2}| he…...

数据分析入门
B站:01第一课 数据分析岗位职责和数据分析师_哔哩哔哩_bilibili 一、岗位:数据分析师 Q1 数据分析师在公司做什么工作? 数据来源于公司核心业务,通过监测业务健康度来确定业务的健康状况; 通过对用户精细化分析&am…...
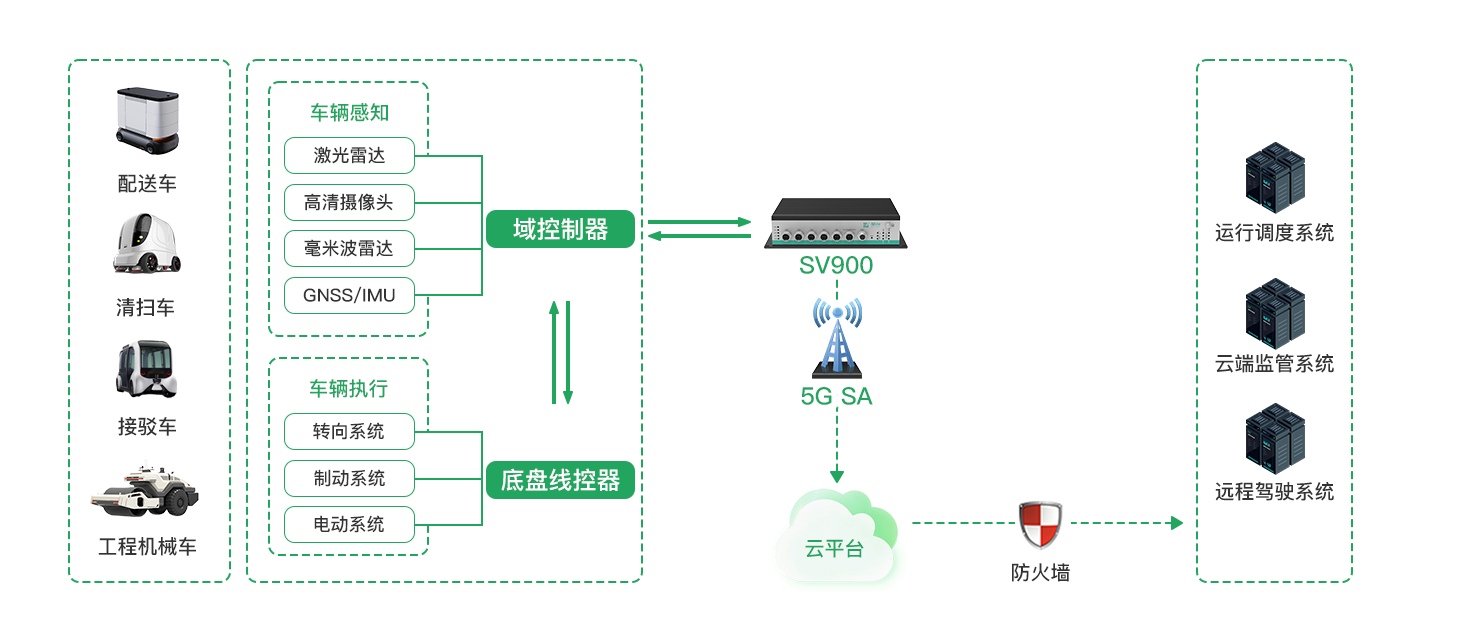
车载网关通信能力解析——SV900-5G车载网关推荐
随着车联网的发展,各类车载设备对车载网关的需求日益增长。车载网关作为车与车、车与路、车与云之间连接的关键设备,其通信能力直接影响整个系统的性能。本文将详细解析车载网关的通信能力,并推荐性价比高的SV900-5G车载网关。 链接直达:https://www.key-iot.com/i…...

服务器中了mkp勒索病毒怎么处理,mkp勒索病毒解密,数据恢复
10月份以来,云天数据恢复中心陆续接到很多企业的求助,企业的服务器遭到了mkp勒索病毒攻击,导致企业的服务器数据库被加密,严重影响了企业工作,通过这一波mkp勒索病毒的攻击,云天数据恢复工程师为大家总结了…...

义乌再次位列第一档!2022年跨境电商综试区评估结果揭晓!
义乌跨境电商综试区捷报频传,在商务部公布的“2022年跨境电子商务综合试验区评估”结果中,中国(义乌)跨境电子商务综合试验区(以下简称:“跨境综试区”)评估结果为成效明显,综合排名…...
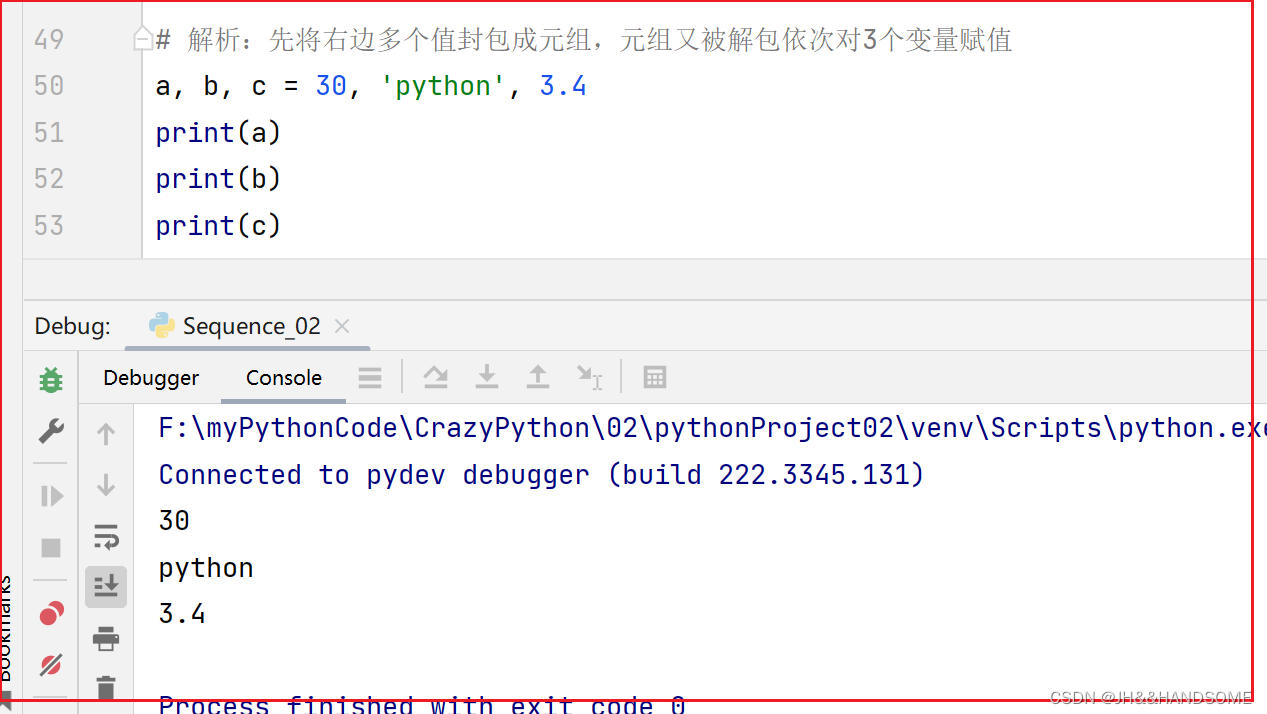
07、Python -- 序列相关函数与封包解包
目录 使用函数字符串也能比较大小序列封包序列解包多变量同时赋值 最大值、最小值、长度 序列解包与封包 使用函数 len()、max()、min() 函数可获取元组、列表的长度、最大值和最小值。 字符串也能比较大小 字符串比较大小时,将会依次按字符串中每个字符对应的编…...
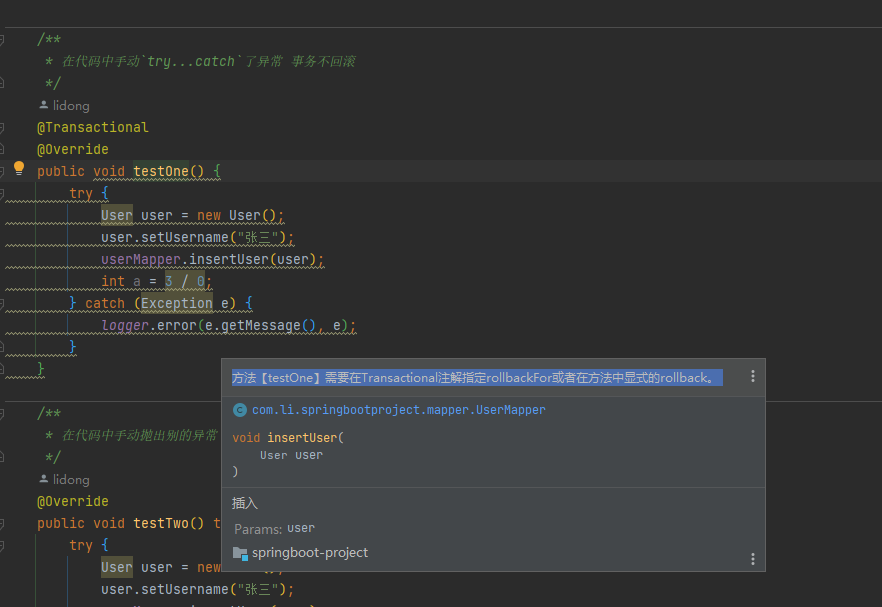
# Spring 事务失效场景
Spring 事务失效场景 文章目录 Spring 事务失效场景前言事务不生效未开启事务事务方法未被Spring管理访问权限问题基于接口的代理源码解读 CGLIB代理 方法用final修饰同一类中的方法调用多线程调用不支持事务 事务不回滚设置错误的事务传播机制捕获了异常手动抛了别的异常自定义…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
