统计学习方法 拉格朗日对偶性
文章目录
- 统计学习方法 拉格朗日对偶性
- 原始问题
- 对偶问题
- 原始问题和对偶问题的关系
统计学习方法 拉格朗日对偶性
读李航的《统计学习方法》时,关于拉格朗日对偶性的笔记。
在许多统计学习的约束最优化问题中,例如最大熵模型和支持向量机,常常使用拉格朗日对偶性(Lagrange duality)将原始问题转换为对偶问题,通过求解对偶问题而得到原始问题的解。
原始问题
假设 f ( x ) f(x) f(x) , c i ( x ) c_i(x) ci(x) 和 h j ( x ) h_j(x) hj(x) 是定义在 R n \R^n Rn 上的连续可微函数,考虑约束最优化问题(记为 P P P ):
min x ∈ R n f ( x ) s.t. c i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , k h j ( x ) = 0 , j = 1 , 2 , ⋯ , l \begin{aligned} \min_{x\in\R^n}&\, f(x) \\ \text{s.t.}&\,\, c_i(x)\leq 0,\quad i=1,2,\cdots,k \\ &\,\, h_j(x)=0, \quad j=1,2,\cdots,l \end{aligned} x∈Rnmins.t.f(x)ci(x)≤0,i=1,2,⋯,khj(x)=0,j=1,2,⋯,l
它的 Lagrangian 为:
L ( x , α , β ) = f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) L(x,\alpha,\beta)=f(x)+\sum_{i=1}^{k}\alpha_ic_i(x)+\sum\limits_{j=1}^l \beta_jh_j(x) L(x,α,β)=f(x)+i=1∑kαici(x)+j=1∑lβjhj(x)
其中 α i ≥ 0 \alpha_i \geq 0 αi≥0 ;以下是一个关于 x x x 的函数,下标 P P P 代表原始问题:
θ P ( x ) = max α , β ; α i ≥ 0 L ( x , α , β ) \theta_P(x)=\max\limits_{\alpha,\beta;\,\alpha_i\geq0}L(x,\alpha,\beta) θP(x)=α,β;αi≥0maxL(x,α,β)
可以得到该函数的性质:
θ P ( x ) = { f ( x ) , x 满足原始问题的约束 + ∞ , else \theta_P(x)=\left\{ \begin{array}{ll} f(x), & x\text{ 满足原始问题的约束} \\ +\infty, &\text{else} \end{array} \right. θP(x)={f(x),+∞,x 满足原始问题的约束else
- 如果 x x x 不满足原始问题的约束,即存在某个 i i i 使得 c i ( x ) > 0 c_i(x)\gt 0 ci(x)>0 或者存在某个 j j j 使得 h j ( x ) ≠ 0 h_j(x)\not=0 hj(x)=0 ,那么就有:
- 若存在某个 i i i 使得 c i ( x ) > 0 c_i(x)\gt 0 ci(x)>0 :我们令 α i → + ∞ \alpha_i\to+\infty αi→+∞ ,则 θ P ( θ ) → + ∞ \theta_P(\theta)\to+\infty θP(θ)→+∞ ;
- 若存在某个 j j j 使得 h j ( x ) ≠ 0 h_j(x)\not=0 hj(x)=0 :我们令 β j \beta_j βj 取和 h j ( x ) h_j(x) hj(x) 相同的符号,并且令 ∣ β j ∣ → + ∞ |\beta_j|\to+\infty ∣βj∣→+∞ ,即 β j h j ( x ) → + ∞ \beta_jh_j(x)\to+\infty βjhj(x)→+∞ ,则 θ P ( θ ) → + ∞ \theta_P(\theta)\to+\infty θP(θ)→+∞ ;
θ P ( x ) = max α , β ; α i ≥ 0 [ f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) ] = + ∞ \theta_P(x)=\max\limits_{\alpha,\beta;\,\alpha_i\geq0}\left[f(x)+\sum_{i=1}^{k}\alpha_ic_i(x)+\sum\limits_{j=1}^l \beta_jh_j(x)\right]=+\infty θP(x)=α,β;αi≥0max[f(x)+i=1∑kαici(x)+j=1∑lβjhj(x)]=+∞
- 若 x x x 满足原始问题的约束,则 ∑ i = 1 k α i c i ( x ) ≤ 0 \sum\limits_{i=1}^{k}\alpha_ic_i(x)\leq 0 i=1∑kαici(x)≤0 , ∑ j = 1 l β j h j ( x ) = 0 \sum\limits_{j=1}^l \beta_jh_j(x)=0 j=1∑lβjhj(x)=0 ,因此:
θ P ( x ) = f ( x ) \theta_P(x)=f(x) θP(x)=f(x)
基于 θ P ( x ) \theta_P(x) θP(x) 的性质,我们考虑其极小化问题:
min x θ P ( x ) = min x max α , β ; α i ≥ 0 L ( x , α , β ) \min_{x}\theta_P(x)=\min_{x}\max\limits_{\alpha,\beta;\,\alpha_i\geq0}L(x,\alpha,\beta) xminθP(x)=xminα,β;αi≥0maxL(x,α,β)
它与原始问题 P P P 是等价的(因为 x x x 满足约束条件时, θ P ( x ) \theta_P(x) θP(x) 和 f ( x ) f(x) f(x) 是等价的)。以上这个问题称为广义拉格朗日函数的极小极大问题。我们定义原始问题的最优值:
p ∗ = min x θ P ( x ) p^\ast=\min_x\theta_P(x) p∗=xminθP(x)
称为原始问题的值。
对偶问题
以下是一个关于 α \alpha α 和 β \beta β 的函数,下标 D D D 代表对偶问题:
θ D ( α , β ) = min x L ( x , α , β ) \theta_D(\alpha,\beta)=\min_xL(x,\alpha,\beta) θD(α,β)=xminL(x,α,β)
再考虑 θ D ( α , β ) \theta_D(\alpha,\beta) θD(α,β) 的极大化问题:
max α , β ; α i ≥ 0 θ D ( α , β ) = max α , β ; α i ≥ 0 min x L ( x , α , β ) \max\limits_{\alpha,\beta;\,\alpha_i\geq0}\theta_D(\alpha,\beta)=\max\limits_{\alpha,\beta;\,\alpha_i\geq0}\min_xL(x,\alpha,\beta) α,β;αi≥0maxθD(α,β)=α,β;αi≥0maxxminL(x,α,β)
该问题称为广义拉格朗日函数的极大极小问题,其还可以表示为约束最优化问题:
max α , β ; α i ≥ 0 θ D ( α , β ) = max α , β ; α i ≥ 0 min x L ( x , α , β ) s.t. α i ≥ 0 , i = 1 , 2 , ⋯ , k \begin{aligned} \max\limits_{\alpha,\beta;\,\alpha_i\geq0}&\, \theta_D(\alpha,\beta)=\max\limits_{\alpha,\beta;\,\alpha_i\geq0}\min_xL(x,\alpha,\beta) \\ \text{s.t.}&\,\, \alpha_i\geq 0, \quad i=1,2,\cdots,k \end{aligned} α,β;αi≥0maxs.t.θD(α,β)=α,β;αi≥0maxxminL(x,α,β)αi≥0,i=1,2,⋯,k
极大极小问题称为原始问题的对偶问题,定义对偶问题的最优值为:
d ∗ = max α , β ; α i ≥ 0 θ D ( α , β ) d^\ast=\max\limits_{\alpha,\beta;\,\alpha_i\geq0}\theta_D(\alpha,\beta) d∗=α,β;αi≥0maxθD(α,β)
称为对偶问题的值。
原始问题和对偶问题的关系
Th C.1:若原始问题和对偶问题都有最优值,则对偶问题的最优值小于等于原始问题的最优值:
d ∗ ≤ p ∗ d^\ast \leq p^\ast d∗≤p∗
证明:由前面的定义得,对于任意的 α \alpha α , β \beta β , x x x ,有:
θ D ( α , β ) = min x L ( x , α , β ) ≤ L ( x , α , β ) ≤ max α , β ; α i ≥ 0 L ( x , α , β ) = θ P ( x ) \theta_D(\alpha,\beta)=\min_xL(x,\alpha,\beta)\leq L(x,\alpha,\beta)\leq\max\limits_{\alpha,\beta;\,\alpha_i\geq0}L(x,\alpha,\beta)=\theta_P(x) θD(α,β)=xminL(x,α,β)≤L(x,α,β)≤α,β;αi≥0maxL(x,α,β)=θP(x)
即:
θ D ( α , β ) ≤ θ P ( x ) \theta_D(\alpha,\beta)\leq\theta_P(x) θD(α,β)≤θP(x)
即:
d ∗ = max α , β ; α i ≥ 0 θ D ( α , β ) ≤ min x θ P ( x ) = p ∗ d^\ast=\max\limits_{\alpha,\beta;\,\alpha_i\geq0}\theta_D(\alpha,\beta)\leq\min_x\theta_P(x)=p^\ast d∗=α,β;αi≥0maxθD(α,β)≤xminθP(x)=p∗
推论 C.1:设 x ∗ x^\ast x∗ 和 α ∗ \alpha^\ast α∗ , β ∗ \beta^\ast β∗ 分别是原始问题和最优问题的可行解(即满足约束条件),且 d ∗ = p ∗ d^\ast=p^\ast d∗=p∗ ,则 x ∗ x^\ast x∗ 和 α ∗ \alpha^\ast α∗ , β ∗ \beta^\ast β∗ 分别是原始问题和最优问题的最优解。
Th C.2:对于原始问题和对偶问题,假设:
- 函数 f ( x ) f(x) f(x) 和 c i ( x ) c_i(x) ci(x) 是凸函数, h j ( x ) h_j(x) hj(x) 是仿射函数;
- 存在 x x x ,对于任意 i i i ,满足 c i ( x ) < 0 c_i(x)\lt 0 ci(x)<0 (即不等式约束 c i ( x ) c_i(x) ci(x) 严格可行);
则存在 x ∗ x^\ast x∗ , α ∗ \alpha^\ast α∗ , β ∗ \beta^\ast β∗ ,使得 x ∗ x^\ast x∗ 是原始问题的解, α ∗ \alpha^\ast α∗ , β ∗ \beta^\ast β∗ 是对偶问题的解,并且:
p ∗ = d ∗ = L ( x ∗ , α ∗ , β ∗ ) p^\ast=d^\ast=L(x^\ast,\alpha^\ast,\beta^\ast) p∗=d∗=L(x∗,α∗,β∗)
Th C.3:跟 Th C.2 一样的假设下, x ∗ x^\ast x∗ 和 α ∗ \alpha^\ast α∗ , β ∗ \beta^\ast β∗ 分别是原始问题和最优问题的可行解的充分必要条件是: x ∗ x^\ast x∗ , α ∗ \alpha^\ast α∗ , β ∗ \beta^\ast β∗ 满足 KKT 条件:
∇ x L ( x ∗ , α ∗ , β ∗ ) = 0 α i ∗ c i ( x ∗ ) = 0 , i = 1 , 2 , ⋯ , k c i ( x ∗ ) ≤ 0 , i = 1 , 2 , ⋯ , k α i ∗ ≥ 0 , i = 1 , 2 , ⋯ , k h j ( x ∗ ) = 0 , j = 1 , 2 , ⋯ , k \begin{array}{c} \nabla_x L(x^\ast,\alpha^\ast,\beta^\ast)=0 \\ \alpha_i^\ast c_i(x^\ast)=0, \quad i=1,2,\cdots,k \\ c_i(x^\ast)\leq 0, \quad i=1,2,\cdots,k \\ \alpha_i^\ast \geq 0, \quad i=1,2,\cdots,k \\ h_j(x^\ast)=0, \quad j=1,2,\cdots,k \\ \end{array} ∇xL(x∗,α∗,β∗)=0αi∗ci(x∗)=0,i=1,2,⋯,kci(x∗)≤0,i=1,2,⋯,kαi∗≥0,i=1,2,⋯,khj(x∗)=0,j=1,2,⋯,k
其中 α i ∗ c i ( x ∗ ) = 0 , i = 1 , 2 , ⋯ , k \alpha_i^\ast c_i(x^\ast)=0, \quad i=1,2,\cdots,k αi∗ci(x∗)=0,i=1,2,⋯,k 称为 KKT 的对偶互补条件。由此可知,若 α i > 0 \alpha_i \gt 0 αi>0 ,则 c i ( x ∗ ) = 0 c_i(x^\ast)=0 ci(x∗)=0 ;
相关文章:

统计学习方法 拉格朗日对偶性
文章目录 统计学习方法 拉格朗日对偶性原始问题对偶问题原始问题和对偶问题的关系 统计学习方法 拉格朗日对偶性 读李航的《统计学习方法》时,关于拉格朗日对偶性的笔记。 在许多统计学习的约束最优化问题中,例如最大熵模型和支持向量机,常…...
.rancher-pipeline.yml
一、注意点 其实下文二的image是基于这个镜像作为基础镜像在这个镜像中执行打包,shellScript 当前路径是你代码块与上图settings.xml,图中的settings.xml可以替换下你当前镜像的settings.xml 示例 二、.rancher-pipeline.yml ${CICD_GIT_BRANCH}这些从官…...
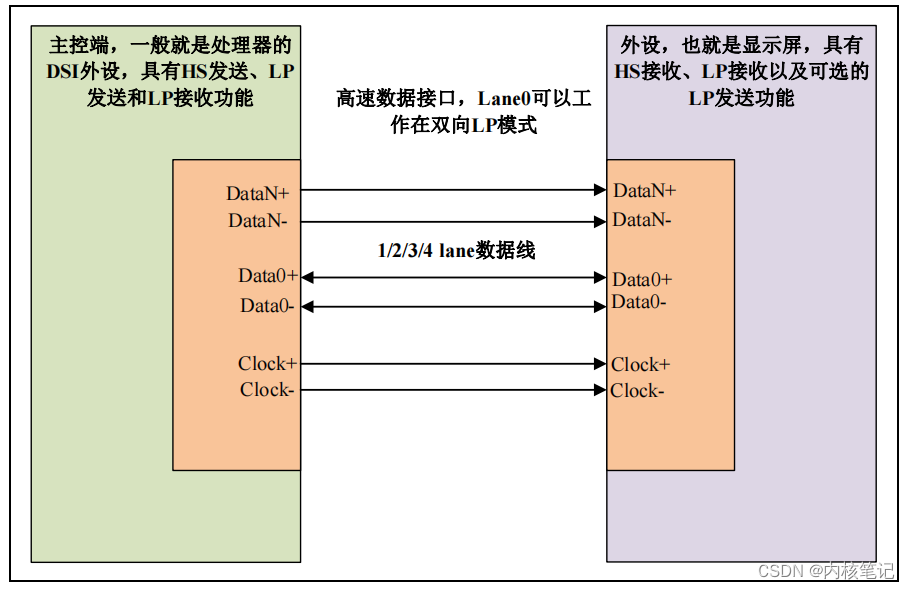
RK3588平台开发系列讲解(显示篇)MIPI DSI协议介绍之分层
🚀返回专栏总目录 文章目录 一、MIPI DSI 分层1.1、应用层1.2、协议层1.3、链路层1.4、物理层沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 DSI 全称是 Display Serial Interface,是主控和显示模组之间的串行连接接口。 MIPI DSI 接口分为数据线和时钟线,均为…...

前端学成在线项目详细解析三
19-推荐课程-内容样式 HTML结构 <ul><li><a href"#"><div class"pic"><img src"./uploads/course01.png" alt""></div><div class"text"><h4>JavaScript数据看板项目实战…...
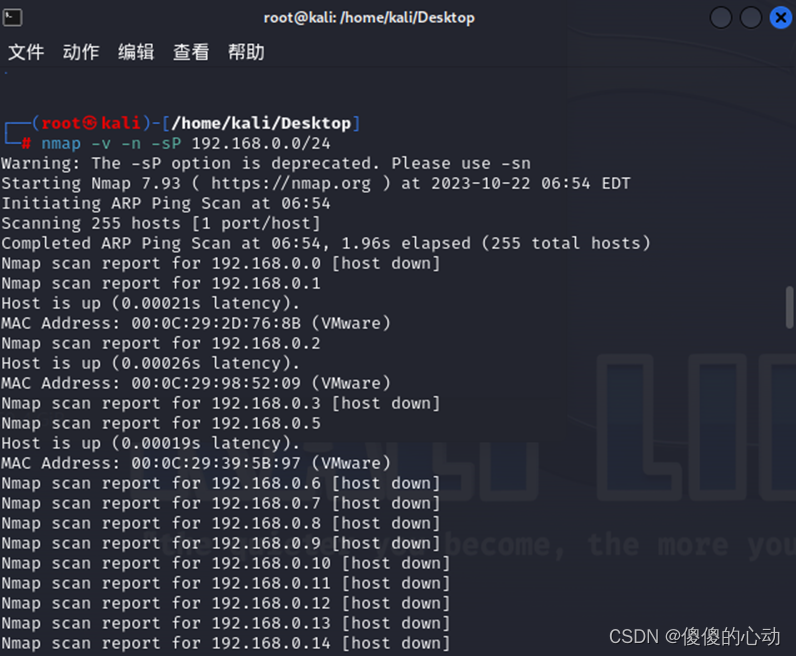
使用Kali进行实验---主机发现
主机发现 【实训目的】 掌握主机扫描的工作原理,学会使用ping等扫描工具,发现网络当中活跃的主机。 【场景描述】 在虚拟机环境下配置4个虚拟系统“Win XP1” “Win XP2” “Kali Linux”和“Metasploitable2”,使得4个系统之间能够相互通…...
)
美团笔试真题2023第一场(4题)
点评: 题目总体来说偏向于中下难度 1.字符串前缀 题目描述: 现在有两个字符串S和T,你需要对S进行若干次操作,使得S是T的一个前缀(空串也是一个前缀)。每次操作可以修改S的一个字符,或者删除一个…...
分隔符(delimiters) 使用)
PHP explode (多)分隔符(delimiters) 使用
PHP explode (多)分隔符(delimiters) 使用 问题:[https://blog.csdn.net/YBaog?typeblog] 把链接中所有的字符串取出。 ㊙️ 神秘算法 ㊙️ function multi_explode($delimiters, $string) {$data [];if ($string) {$str str_replace($delimiters, $delimiter…...

AI的Prompt是什么
一.AI的Prompt的作用 在人工智能(AI)中,"Prompt"通常指的是向AI系统提供的输入或指令,用于引导AI进行特定的操作或生成特定的输出。例如,在一个对话型AI系统中,用户输入的问题就是一个prompt&…...

Qt之自定义model读写CSV文件
一.效果 本文基于QAbstractTableModel实现了一个支持读写CSV文件的TableModel。CSV数据格式虽然很简单,但是网上大多数读写方式其实都是有bug的,没考虑到字段里包含逗号或换行符这种复杂数据的情况。 二.原理 CSV(Comma-Separated Values)文件是一种简单类型的纯文本文件…...
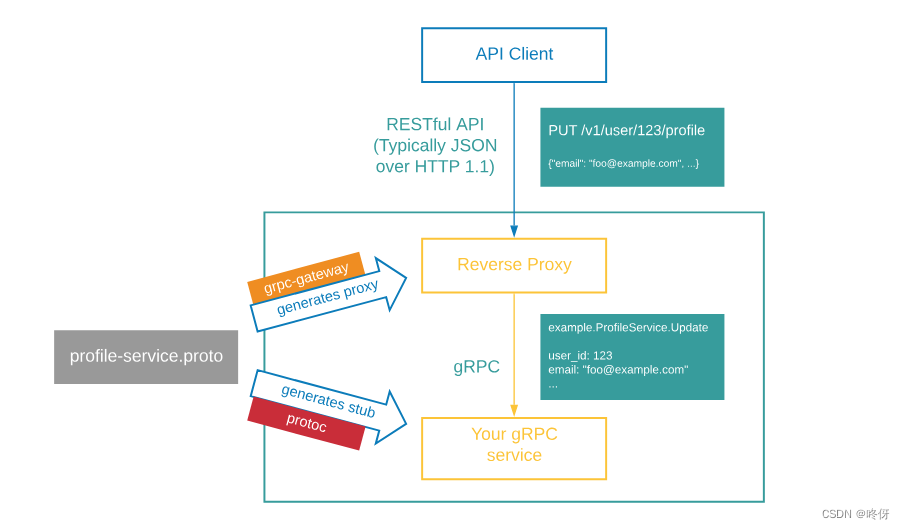
golang 工程组件:grpc-gateway 环境安装+默认网关测试
grpc-gateway grpc-gateway 顾名思义是专门是grpc的网关。也是一个protobuf的编译器,是一个proto的插件。 grpc-gateway就是将http请求处理后转发到对应grpc服务上。很多浏览器,或者客户端开箱不支持grpc,只支持传统的restful API。 grpc网关…...

IP地址SSL证书 IP证书
在许多企业用例中,公司需要SSL证书作为IP地址。公司使用IP地址通过Internet访问各种类型的应用程序。 公网IP地址的SSL证书: 内部IP(也称为私有IP)是IANA设置为保存的IPv4或IPv6地址,例如: RFC 1918范围内…...

MVCC 过程中会加锁吗?
MVCC 机制,全称(Multi-Version Concurrency Control)多版本并发控制,是确保 在高并发下, 多个事务读取数据时不加锁也可以多次读取相同的值。 MVCC 在读已提交(READ COMMITTED)、可重复读&…...
NLP入门——语言结构/语言建模
一、Linguistics 语言学 wordsmorphology 形态学:词的构成和内部结构研究。如英语的dog、dogs和dog-catcher有相当的关系morpheme 语素:最小的语法单位,是最小的音义结合体lexeme 词位:词的意义的基本抽象单位,是一组…...

2023java攻克了抖音视频去水印视频下载
2023java攻克了抖音视频去水印视频下载 1、过滤链接 /*** 过滤链接,获取http连接地址* param url* return*/public static String decodeHttpUrl(String url) {int start url.indexOf("http");int end url.lastIndexOf("/");String decodeu…...

云计算要学习哪些技术?
学习云计算需要涉及多个技术领域和相关的工具、平台和框架。以下是一个详细的介绍,帮助您了解学习云计算所需的技术。 1. 虚拟化技术 虚拟化是云计算的基础,因此了解虚拟化技术至关重要。学习虚拟化技术时,需要掌握以下知识点: …...

Spring bean 和 Java Bean的区别
Spring bean 和 Java Bean的区别 一,JavaBean JavaBean 是一种特殊的 Java 类,遵循一定的命名规范和属性访问规范。它是一种用于表示简单数据类型、封装业务逻辑或与其他对象交互的可重用组件。 JavaBean 必须满足以下规范: 公共无参构造方…...

性能测试 —— Jmeter 命令行详细
我们在启动Jmeter时 会看见:Don’t use GUI mode for load testing !, only for Test creation and Test debugging.For load testing, use CLI Mode (was NON GUI) 这句话的意思就是说,不要使用gui模式进行负载测试,gui模式仅仅是创建脚本…...

ChatGPT AIGC 办公自动化拆分Excel工作表
在职场办公中对数据的操作,经常需要将一份表格数据拆分成多个表。 但是在Excel中进行表格拆分的步骤比较多。 在Excel中拆分工作表的步骤: 1.打开您的Excel工作簿,选择您要拆分的工作表。 2.右键单击工作表标签(通常在底部),选择“移动或复制”。 3.在“移动或复制”…...

Web前端—Flex布局:标准流、浮动、Flex布局、综合案例(短视频首页解决方案)
版本说明 当前版本号[20231024]。 20231024初版 目录 文章目录 版本说明目录Flex布局01-标准流02-浮动基本使用产品区域布局HTML标签CSS样式 清除浮动场景搭建额外标签法单伪元素法双伪元素法overfow法 03-Flex布局Flex组成主轴对齐方式侧轴对齐方式修改主轴方向弹性伸缩比弹…...

【Git LFS】huggingface 断点续传
这里有个很好的介绍:https://stackoverflow.com/questions/72610494/what-is-the-difference-between-git-lfs-fetch-git-lfs-fetch-all-and-git 提供的信息是关于如何作为普通用户使用Git LFS(Large File Storage),涵盖了各种Gi…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
