AM@两种余项型泰勒公式的对比和总结@常用函数的麦克劳林公式
文章目录
- abstract
- 两种余项型泰勒公式的对比和总结
- Maclaurin公式
- 常用函数的Maclaurin公式
- 推导
- 例
- 求极限
- 按幂展开
abstract
- 泰勒公式的两种余项型(Penao&Lagrange)泰勒公式的对比和总结
- 常用的Maclaurin公式列举(Peano余项型为主)
两种余项型泰勒公式的对比和总结
-
Taylor公式 Lagrange型 Peano项 Note 条件 [ a , b ] [a,b] [a,b]上有 n n n阶连续导数, ( a , b ) (a,b) (a,b)内存在 n + 1 n+1 n+1阶导数 x = x 0 x=x_0 x=x0处存在 n n n阶导数 前者对 f ( x ) f(x) f(x)要求较高 余项 R n ( x ) R_n(x) Rn(x)= f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} (n+1)!f(n+1)(ξ)(x−x0)n+1或 f ( n + 1 ) ( θ x ) ( n + 1 ) ! ( x − x 0 ) n + 1 \frac{f^{(n+1)}(\theta x)}{(n+1)!}(x-x_0)^{n+1} (n+1)!f(n+1)(θx)(x−x0)n+1, θ ∈ ( 0 , 1 ) \theta\in(0,1) θ∈(0,1) R n ( x ) R_n(x) Rn(x)= o ( ( x − x 0 ) n ) o((x-x_0)^{n}) o((x−x0)n) 前者余项具体,后者仅表达了高阶无穷小 用途 可用于区间 [ a , b ] [a,b] [a,b]上,例如证明不等式或等式,估计逼近误差 仅用于 x 0 x_0 x0的邻域 U ( x 0 ) U(x_0) U(x0),例如讨论极值,求解 x → x 0 x\to{x_0} x→x0时的极限 后者用在某些条件下的求极限问题上,可以带来方便
Maclaurin公式
- 这里主要讨论Peano型Maclaurin公式(一般不要求计算误差精度,Peano型足够使用)
- f ( x ) f(x) f(x)= f ( 0 ) + f ′ ( 0 ) x + 1 2 ! f ′ ′ ( 0 ) x 2 f(0)+f'(0)x+\frac{1}{2!}f''(0)x^2 f(0)+f′(0)x+2!1f′′(0)x2+ ⋯ \cdots ⋯+ 1 n ! f ( n ) ( 0 ) x n \frac{1}{n!}f^{(n)}(0)x^n n!1f(n)(0)xn+ R n ( x ) R_n(x) Rn(x)
(1),两种余项分别为:- R n ( x ) R_n(x) Rn(x)= o ( x n ) o(x^{n}) o(xn)
(1-1) - R n ( x ) R_n(x) Rn(x)= f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} (n+1)!f(n+1)(ξ)(x−x0)n+1或 f ( n + 1 ) ( θ x ) ( n + 1 ) ! ( x − x 0 ) n + 1 \frac{f^{(n+1)}(\theta x)}{(n+1)!}(x-x_0)^{n+1} (n+1)!f(n+1)(θx)(x−x0)n+1, θ ∈ ( 0 , 1 ) \theta\in(0,1) θ∈(0,1)
(1-2)
- R n ( x ) R_n(x) Rn(x)= o ( x n ) o(x^{n}) o(xn)
常用函数的Maclaurin公式
-
主要掌握展开公式的前几项(2到5项,一般3项)就足够一般的应用,
-
只要知道公式
(1),和 f ( x ) f(x) f(x)的高阶导数,在必要的时候可以自行计算更多的项- e x e^{x} ex= 1 + x + 1 2 ! x 2 + ⋯ + 1 n ! x n 1+x+\frac{1}{2!}x^2+\cdots+\frac{1}{n!}x^{n} 1+x+2!1x2+⋯+n!1xn+ o ( x n ) o(x^{n}) o(xn)
- sin x \sin{x} sinx= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7} x−3!1x3+5!1x5−7!1x7+ ⋯ \cdots ⋯+ ( − 1 ) n ( 2 n − 1 ) ! x 2 n − 1 \frac{(-1)^{n}}{(2n-1)!}x^{2n-1} (2n−1)!(−1)nx2n−1+ o ( x 2 n − 1 ) o(x^{2n-1}) o(x2n−1)
- cos x \cos{x} cosx= 1 − 1 2 ! x 2 + 1 4 ! x 4 − 1 6 ! x 6 1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^{6} 1−2!1x2+4!1x4−6!1x6+ ⋯ \cdots ⋯+ ( − 1 ) n ( 2 n ) ! x 2 n \frac{(-1)^{n}}{(2n)!}x^{2n} (2n)!(−1)nx2n+ o ( x 2 n ) o(x^{2n}) o(x2n)
- ln ( 1 + x ) \ln{(1+x)} ln(1+x)= x − x 2 2 + x 3 3 − x 5 5 x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^5}{5} x−2x2+3x3−5x5+ ⋯ \cdots ⋯+ ( − 1 ) n − 1 x n n (-1)^{n-1}\frac{x^{n}}{n} (−1)n−1nxn+ o ( x n ) o(x^{n}) o(xn)
- ( 1 + x ) m (1+x)^{m} (1+x)m= 1 + m x + m ( m − 1 ) 2 ! x 2 1+mx+\frac{m(m-1)}{2!}x^2 1+mx+2!m(m−1)x2+ ⋯ \cdots ⋯+ m ( m − 1 ) ⋯ ( m − n + 1 ) n ! x n \frac{m(m-1)\cdots(m-n+1)}{n!}x^{n} n!m(m−1)⋯(m−n+1)xn+ o ( x n ) o(x^{n}) o(xn)
-
其中偶(奇)函数的展开式也是偶(奇)函数
- 上述公式3,4有时也写作
- sin x \sin{x} sinx= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7} x−3!1x3+5!1x5−7!1x7+ ⋯ \cdots ⋯+ ( − 1 ) n ( 2 n + 1 ) ! x 2 n + 1 \frac{(-1)^{n}}{(2n+1)!}x^{2n+1} (2n+1)!(−1)nx2n+1+ o ( x 2 n + 2 ) o(x^{2n+2}) o(x2n+2)
- 余项前的一项的幂是奇次幂 k k k即可( 2 n + 1 2n+1 2n+1或 2 n − 1 2n-1 2n−1),Peano余项的幂次数可以 o ( x k ) o(x^{k}) o(xk)或 o ( x k + 1 ) o(x^{k+1}) o(xk+1)
- cos x \cos{x} cosx= 1 − 1 2 ! x 2 + 1 4 ! x 4 − 1 6 ! x 6 1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^{6} 1−2!1x2+4!1x4−6!1x6+ ⋯ \cdots ⋯+ ( − 1 ) n ( 2 n ) ! x 2 n \frac{(-1)^{n}}{(2n)!}x^{2n} (2n)!(−1)nx2n+ o ( x 2 n + 1 ) o(x^{2n+1}) o(x2n+1)
- 余项前的一项的幂是偶次幂,通常表示为 2 n 2n 2n,Peano余项的幂次数可以是 o ( x 2 n ) o(x^{2n}) o(x2n)或 o ( x 2 n + 1 ) o(x^{2n+1}) o(x2n+1)
- sin x \sin{x} sinx= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7} x−3!1x3+5!1x5−7!1x7+ ⋯ \cdots ⋯+ ( − 1 ) n ( 2 n + 1 ) ! x 2 n + 1 \frac{(-1)^{n}}{(2n+1)!}x^{2n+1} (2n+1)!(−1)nx2n+1+ o ( x 2 n + 2 ) o(x^{2n+2}) o(x2n+2)
- 上述公式3,4有时也写作
-
其中余项不是 x n x^{n} xn的公式都是经过简并后的公式(把值为0的项隐后剩下的项重新编排 i = 0 , 1 , 2 , i=0,1,2, i=0,1,2,)
-
注意到,上述公式挂等号的前提是带上余项,反之,带上余项的展开式可以直接被展开函数参与某这些运算(比如求极限)
推导
-
按照 f ( x ) f(x) f(x)的 n n n阶导数公式和 f ( x ) f(x) f(x)的 n n n阶Maclaurin公式推导即可
-
以 sin x \sin{x} sinx为例推导:
- f ( n ) ( x ) f^{(n)}(x) f(n)(x)= ( sin x ) ( n ) (\sin{x})^{(n)} (sinx)(n)= sin ( x + n π 2 ) \sin{(x+\frac{n\pi}{2})} sin(x+2nπ);
(2-1) - f ( n ) ( 0 ) f^{(n)}(0) f(n)(0)= ( sin x ) ( n ) ∣ x = 0 (\sin{x})^{(n)}|_{x=0} (sinx)(n)∣x=0= sin ( n π 2 ) \sin{(\frac{n\pi}{2})} sin(2nπ)
(2-2)
n n n f ( n ) ( 0 ) f^{(n)}(0) f(n)(0) 0 0 1 1 1 1 2 0 3 -1 4 0 5 1 6 0 ⋯ \cdots ⋯ ⋯ \cdots ⋯ 根据上述列举和三角函数的知识可知, f ( n ) ( 0 ) f^{(n)}(0) f(n)(0), n = 0 , 1 , 2 , ⋯ n=0,1,2,\cdots n=0,1,2,⋯会循环得取4个数 0 , 1 , 0 , − 1 0,1,0,-1 0,1,0,−1,j记为序列
(S1)有Maclaurin公式可知, f ( n ) ( 0 ) = 0 f^{(n)}(0)=0 f(n)(0)=0的项也是0,这些项可以被简并不写-
这样一来,由序列(S1),保留下来的项的幂的次数就不是连续的了,相邻项的次数相差2而不是1
-
不妨设 p n ( x ) p_{n}(x) pn(x)= ∑ i = 0 n a i x n \sum_{i=0}^{n}a_ix^{n} ∑i=0naixn,
- 前 k k k个非0项分别为 a 1 , a 3 , ⋯ , a 2 k − 1 a_1,a_3,\cdots,a_{2k-1} a1,a3,⋯,a2k−1, a 2 i − 1 , i = 1 , ⋯ , k a_{2i-1},i=1,\cdots,k a2i−1,i=1,⋯,k都是非0项
- 另一方面, f ( x ) = a 0 , a 2 , ⋯ , a 2 k f(x)=a_0,a_2,\cdots,a_{2k} f(x)=a0,a2,⋯,a2k都是0
- ∑ i = 0 k a 2 k − 1 \sum_{i=0}^{k}a_{2k-1} ∑i=0ka2k−1= ∑ i = 0 2 k a i \sum_{i=0}^{2k}a_{i} ∑i=02kai即消去0项之前, 2 k − 1 2k-1 2k−1阶泰勒多项式和 2 k 2k 2k阶泰勒多相式相等(余项可以表示为 o ( x 2 k ) o(x^{2k}) o(x2k)
- 为了便于讨论,将 p n ( x ) p_n(x) pn(x)消去0项后的公式记为 q m ( x ) q_m(x) qm(x)= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 + ⋯ x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7}+\cdots x−3!1x3+5!1x5−7!1x7+⋯的项,第 m = 1 , 2 , ⋯ m=1,2,\cdots m=1,2,⋯项记为 b m b_m bm,它们全部对应于非零项,并且容易归纳出: q n ( x ) q_{n}(x) qn(x)的通项 b m = ( − 1 ) m − 1 ( 2 m − 1 ) ! x 2 m − 1 b_m=\frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1} bm=(2m−1)!(−1)m−1x2m−1,次数 2 m − 1 2m-1 2m−1表示该项对应于 p n ( x ) p_n(x) pn(x)中的 2 m − 1 2m-1 2m−1次幂的项(非0),而 n = 2 m n=2m n=2m项则是零项
- 此时将 q m ( x ) q_m(x) qm(x)表示为 q m ( x ) q_m(x) qm(x)= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7} x−3!1x3+5!1x5−7!1x7+ ⋯ \cdots ⋯+ ( − 1 ) m − 1 ( 2 m − 1 ) ! x 2 m − 1 \frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1} (2m−1)!(−1)m−1x2m−1
- 取 m = k m=k m=k,可以得到 2 k − 1 2k-1 2k−1次泰勒多项式
- sin x \sin{x} sinx= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7} x−3!1x3+5!1x5−7!1x7+ ⋯ \cdots ⋯+ ( − 1 ) m − 1 ( 2 m − 1 ) ! x 2 m − 1 \frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1} (2m−1)!(−1)m−1x2m−1+ R 2 m R_{2m} R2m
(3)
-
Lagrange余项:由式(1-2),(2-1),可知 R 2 m ( x ) R_{2m}(x) R2m(x)= sin ( θ x + ( 2 m + 1 ) π 2 ) ( 2 m + 1 ) ! x 2 m + 1 \frac{\sin(\theta{x}+(2m+1)\frac{\pi}{2})}{(2m+1)!}x^{2m+1} (2m+1)!sin(θx+(2m+1)2π)x2m+1
(4)- t ( x ) t(x) t(x)= sin ( θ x + ( 2 m + 1 ) π 2 ) \sin(\theta{x}+(2m+1)\frac{\pi}{2}) sin(θx+(2m+1)2π)= sin ( θ x + m π + π 2 ) \sin(\theta{x}+m\pi+\frac{\pi}{2}) sin(θx+mπ+2π)
- 当 m m m为奇数时, t ( x ) t(x) t(x)= sin ( θ x + π + π 2 ) \sin(\theta{x+\pi+\frac{\pi}{2}}) sin(θx+π+2π)= sin ( θ x − π 2 ) \sin(\theta{x}-\frac{\pi}{2}) sin(θx−2π)= − cos θ x -\cos\theta{x} −cosθx
- 当 m m m为偶数时, t ( x ) t(x) t(x)= sin ( θ x + π 2 ) \sin(\theta{x}+\frac{\pi}{2}) sin(θx+2π)= cos θ x \cos\theta{x} cosθx
- 可以用 ( − 1 ) m (-1)^{m} (−1)m归纳上述符号变化,从而 t ( x ) t(x) t(x)= ( − 1 ) m cos θ x (-1)^{m}\cos{\theta{x}} (−1)mcosθx
- 从而 R 2 m ( x ) R_{2m}(x) R2m(x)= ( − 1 ) m cos θ x ( 2 m + 1 ) ! x 2 m + 1 (-1)^{m}\frac{\cos{\theta{x}}}{(2m+1)!}x^{2m+1} (−1)m(2m+1)!cosθxx2m+1, θ ∈ ( 0 , 1 ) \theta\in(0,1) θ∈(0,1)
(4-1)
- t ( x ) t(x) t(x)= sin ( θ x + ( 2 m + 1 ) π 2 ) \sin(\theta{x}+(2m+1)\frac{\pi}{2}) sin(θx+(2m+1)2π)= sin ( θ x + m π + π 2 ) \sin(\theta{x}+m\pi+\frac{\pi}{2}) sin(θx+mπ+2π)
-
若取 m = 1 m=1 m=1,得近似公式 sin x ∼ x \sin{x}\sim{x} sinx∼x
- 代入(4-1),可知,此时误差为 ∣ R 2 ∣ = ∣ − cos θ x 3 ! x 3 ∣ ⩽ ∣ x ∣ 3 6 |R_2|=|-\frac{\cos\theta{x}}{3!}x^3|\leqslant{\frac{|x|^{3}}{6}} ∣R2∣=∣−3!cosθxx3∣⩽6∣x∣3,其中 ∣ cos θ x ∣ ⩽ 1 |\cos\theta{x}|\leqslant{1} ∣cosθx∣⩽1
-
若 m = 2 m=2 m=2,则可得到 3 3 3次泰勒多项式 ( x − x 3 3 ! ) (x-\frac{x^3}{3!}) (x−3!x3),误差 ∣ R 2 m ∣ ⩽ 1 5 ! ∣ x ∣ 5 |R_{2m}|\leqslant{\frac{1}{5!}|x|^{5}} ∣R2m∣⩽5!1∣x∣5
-
若 m = 3 m=3 m=3,则可得 5 5 5次泰勒多项式 ( x − x 3 3 ! + x 5 5 ! ) (x-\frac{x^3}{3!}+\frac{x^5}{5!}) (x−3!x3+5!x5),误差不超过 1 7 ! ∣ x ∣ 7 \frac{1}{7!}|x|^{7} 7!1∣x∣7
- f ( n ) ( x ) f^{(n)}(x) f(n)(x)= ( sin x ) ( n ) (\sin{x})^{(n)} (sinx)(n)= sin ( x + n π 2 ) \sin{(x+\frac{n\pi}{2})} sin(x+2nπ);
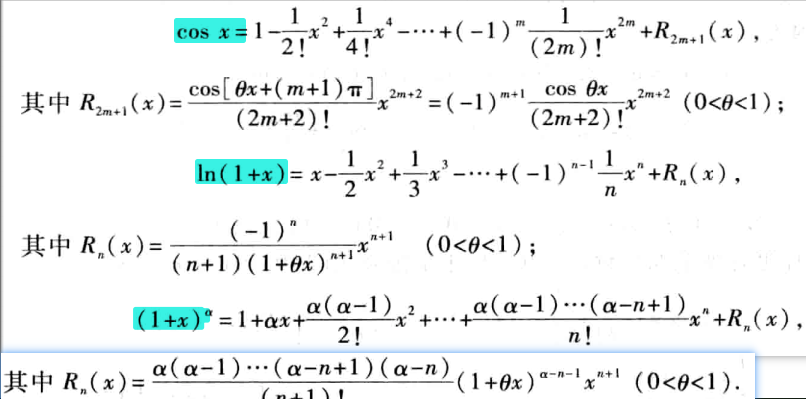
例
求极限
-
求 lim x → 0 sin x − x cos x sin 3 x \lim\limits_{x\to{0}}\frac{\sin{x}-x\cos{x}}{\sin^{3}x} x→0limsin3xsinx−xcosx=A
-
用 sin 3 x ∼ x 3 \sin^3{x}\sim{x^3} sin3x∼x3替换分母
-
解法1:利用等价无穷小替换分母,在利用洛必达法则求解
-
解法2:利用带有Peano余项的Maclaurin公式
- sin x \sin{x} sinx= x − x 3 3 ! + o ( x 3 ) x-\frac{x^3}{3!}+o(x^3) x−3!x3+o(x3);
- cos x = 1 − x 2 2 ! + o ( x 2 ) \cos{x}=1-\frac{x^2}{2!}+o(x^2) cosx=1−2!x2+o(x2); x cos x = x − x 3 2 ! + o ( x 3 ) x\cos{x}=x-\frac{x^3}{2!}+o(x^{3}) xcosx=x−2!x3+o(x3)
- 于是 sin x − x cos x \sin{x}-x\cos{x} sinx−xcosx= x − x 3 3 ! + o ( x 3 ) − ( x + x 3 2 ! + o ( x 3 ) ) x-\frac{x^3}{3!}+o(x^{3})-(x+\frac{x^3}{2!}+o(x^3)) x−3!x3+o(x3)−(x+2!x3+o(x3))= 1 3 x 3 + o ( x 3 ) \frac{1}{3}x^3+o(x^{3}) 31x3+o(x3)
- α ( x ) \alpha(x) α(x)的高阶无穷小 o ( α ( x ) ) , o 1 ( α ( x ) ) o(\alpha(x)),o_1(\alpha(x)) o(α(x)),o1(α(x))之间的和差运算结果仍然是 α ( x ) \alpha(x) α(x)的高阶无穷小( lim o ( α ( x ) ± o 1 ( α ( x ) ) ) α ( x ) \lim\frac{o(\alpha(x)\pm{o_1(\alpha(x))})}{\alpha(x)} limα(x)o(α(x)±o1(α(x)))=0)
- A = lim x → 0 1 3 x 3 + o ( x 3 ) x 3 A=\lim\limits_{x\to{0}}\frac{\frac{1}{3}x^3+o(x^3)}{x^3} A=x→0limx331x3+o(x3)= 1 3 \frac{1}{3} 31
-
按幂展开
f ( x ) = x 3 + 3 x 2 − 2 x + 4 f(x)=x^3+3x^2-2x+4 f(x)=x3+3x2−2x+4的按 ( x + 1 ) (x+1) (x+1)的升幂展开(升幂排列)
-
即按 ( x − ( − 1 ) ) (x-(-1)) (x−(−1))的展开, x 0 = − 1 x_0=-1 x0=−1,得到 g ( x ) g(x) g(x)= ∑ i = 0 3 a i ( x + 1 ) i \sum_{i=0}^{3}a_i(x+1)^{i} ∑i=03ai(x+1)i= ∑ i = 0 3 a i ( x − ( − 1 ) ) i \sum_{i=0}^{3}a_i(x-(-1))^{i} ∑i=03ai(x−(−1))i
-
计算 f ( k ) ( x 0 ) f^{(k)}(x_0) f(k)(x0);
-
由于 f ( x ) f(x) f(x)是个 n = 3 n=3 n=3次的多项式,其泰勒展开也是3次的
-
a i = f ( n ) ( x 0 ) i ! a_i=\frac{f^{(n)}(x_0)}{i!} ai=i!f(n)(x0), i = 0 , 1 , 2 , 3 i=0,1,2,3 i=0,1,2,3
-
a 0 = f ( x 0 ) a_0=f(x_0) a0=f(x0)= 8 8 8
-
f ′ ( x ) = 3 x 2 + 6 x − 2 ; f ′ ( − 1 ) = − 5 f'(x)=3x^2+6x-2;f'(-1)=-5 f′(x)=3x2+6x−2;f′(−1)=−5
-
f ′ ′ ( x ) = 6 x + 6 ; f ′ ′ ( − 1 ) = 0 f''(x)=6x+6;f''(-1)=0 f′′(x)=6x+6;f′′(−1)=0
-
f ( 3 ) ( x ) = 6 ; f ( 3 ) ( − 1 ) = 6 f^{(3)}(x)=6;f^{(3)}(-1)=6 f(3)(x)=6;f(3)(−1)=6
-
f ( k ) ( x ) = 0 ; ( k ⩾ 4 ) f^{(k)}{(x)}=0;(k\geqslant 4) f(k)(x)=0;(k⩾4)
- 所以 R = R 4 ( x ) = 0 R=R_4(x)=0 R=R4(x)=0
-
-
-
f ( x ) = f ( − 1 ) + f ′ ( − 1 ) 1 ! ( x + 1 ) f(x)=f(-1)+\frac{f'(-1)}{1!}(x+1) f(x)=f(−1)+1!f′(−1)(x+1)+ f ′ ′ ( − 1 ) 2 ! ( x + 1 ) 2 \frac{f''(-1)}{2!}(x+1)^2 2!f′′(−1)(x+1)2+ f ( 3 ) ( − 1 ) 3 ! ( x + 1 ) 3 + R 4 ( x ) \frac{f^{(3)}(-1)}{3!}{(x+1)^3}+R_4(x) 3!f(3)(−1)(x+1)3+R4(x)= 8 − 5 ( x + 1 ) + ( x + 1 ) 3 8-5(x+1)+(x+1)^3 8−5(x+1)+(x+1)3
相关文章:
AM@两种余项型泰勒公式的对比和总结@常用函数的麦克劳林公式
文章目录 abstract两种余项型泰勒公式的对比和总结Maclaurin公式常用函数的Maclaurin公式推导例求极限按幂展开 abstract 泰勒公式的两种余项型(Penao&Lagrange)泰勒公式的对比和总结常用的Maclaurin公式列举(Peano余项型为主) 两种余项型泰勒公式的对比和总结 Taylor公式…...

Django实现音乐网站 (22)
使用Python Django框架做一个音乐网站, 本篇音乐播放器功能完善:顺序播放、设置播放数、歌词滚动等功能。 目录 顺序播放 设置顺序播放 单曲播放数 添加路由 视图处理 模板处理 歌词滚动 视图内容返回修改 样式设置 模板内容 歌词滚动脚本 歌…...

pnpm ERR_PNPM_ADDING_TO_ROOT
ERR_PNPM_ADDING_TO_ROOT Running this command will add the dependency to the workspace root, which might not be what you want - if you really meant it, make it explicit by running this command again with the -w flag (or --workspace-root). If you don’t wa…...

统计学习方法 拉格朗日对偶性
文章目录 统计学习方法 拉格朗日对偶性原始问题对偶问题原始问题和对偶问题的关系 统计学习方法 拉格朗日对偶性 读李航的《统计学习方法》时,关于拉格朗日对偶性的笔记。 在许多统计学习的约束最优化问题中,例如最大熵模型和支持向量机,常…...
.rancher-pipeline.yml
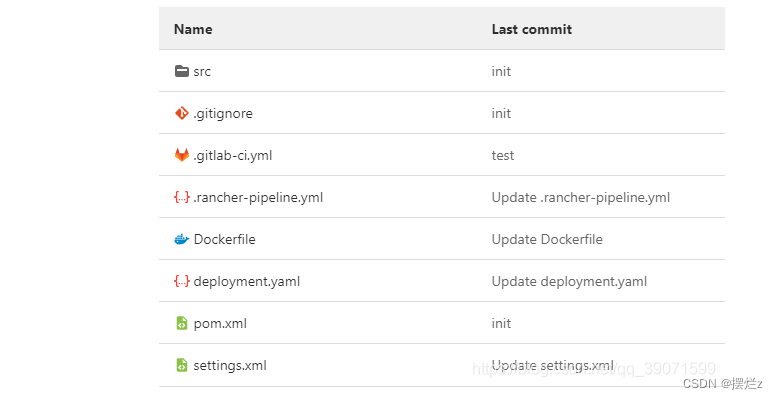
一、注意点 其实下文二的image是基于这个镜像作为基础镜像在这个镜像中执行打包,shellScript 当前路径是你代码块与上图settings.xml,图中的settings.xml可以替换下你当前镜像的settings.xml 示例 二、.rancher-pipeline.yml ${CICD_GIT_BRANCH}这些从官…...
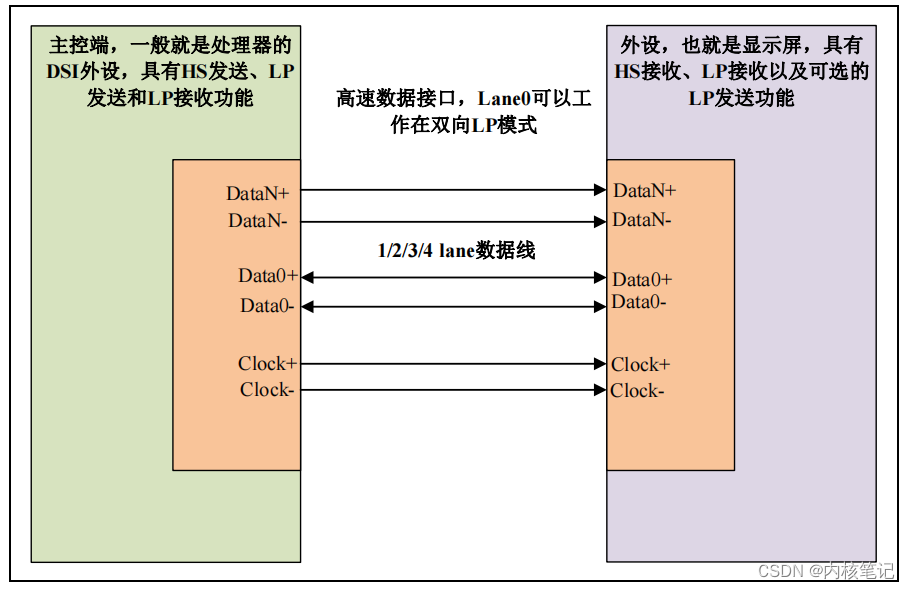
RK3588平台开发系列讲解(显示篇)MIPI DSI协议介绍之分层
🚀返回专栏总目录 文章目录 一、MIPI DSI 分层1.1、应用层1.2、协议层1.3、链路层1.4、物理层沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 DSI 全称是 Display Serial Interface,是主控和显示模组之间的串行连接接口。 MIPI DSI 接口分为数据线和时钟线,均为…...

前端学成在线项目详细解析三
19-推荐课程-内容样式 HTML结构 <ul><li><a href"#"><div class"pic"><img src"./uploads/course01.png" alt""></div><div class"text"><h4>JavaScript数据看板项目实战…...
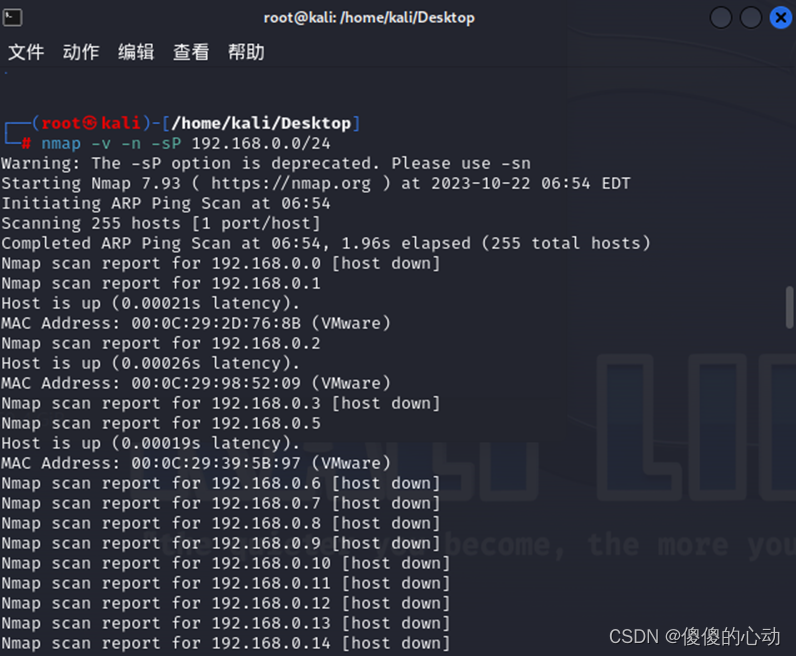
使用Kali进行实验---主机发现
主机发现 【实训目的】 掌握主机扫描的工作原理,学会使用ping等扫描工具,发现网络当中活跃的主机。 【场景描述】 在虚拟机环境下配置4个虚拟系统“Win XP1” “Win XP2” “Kali Linux”和“Metasploitable2”,使得4个系统之间能够相互通…...
)
美团笔试真题2023第一场(4题)
点评: 题目总体来说偏向于中下难度 1.字符串前缀 题目描述: 现在有两个字符串S和T,你需要对S进行若干次操作,使得S是T的一个前缀(空串也是一个前缀)。每次操作可以修改S的一个字符,或者删除一个…...
分隔符(delimiters) 使用)
PHP explode (多)分隔符(delimiters) 使用
PHP explode (多)分隔符(delimiters) 使用 问题:[https://blog.csdn.net/YBaog?typeblog] 把链接中所有的字符串取出。 ㊙️ 神秘算法 ㊙️ function multi_explode($delimiters, $string) {$data [];if ($string) {$str str_replace($delimiters, $delimiter…...

AI的Prompt是什么
一.AI的Prompt的作用 在人工智能(AI)中,"Prompt"通常指的是向AI系统提供的输入或指令,用于引导AI进行特定的操作或生成特定的输出。例如,在一个对话型AI系统中,用户输入的问题就是一个prompt&…...

Qt之自定义model读写CSV文件
一.效果 本文基于QAbstractTableModel实现了一个支持读写CSV文件的TableModel。CSV数据格式虽然很简单,但是网上大多数读写方式其实都是有bug的,没考虑到字段里包含逗号或换行符这种复杂数据的情况。 二.原理 CSV(Comma-Separated Values)文件是一种简单类型的纯文本文件…...
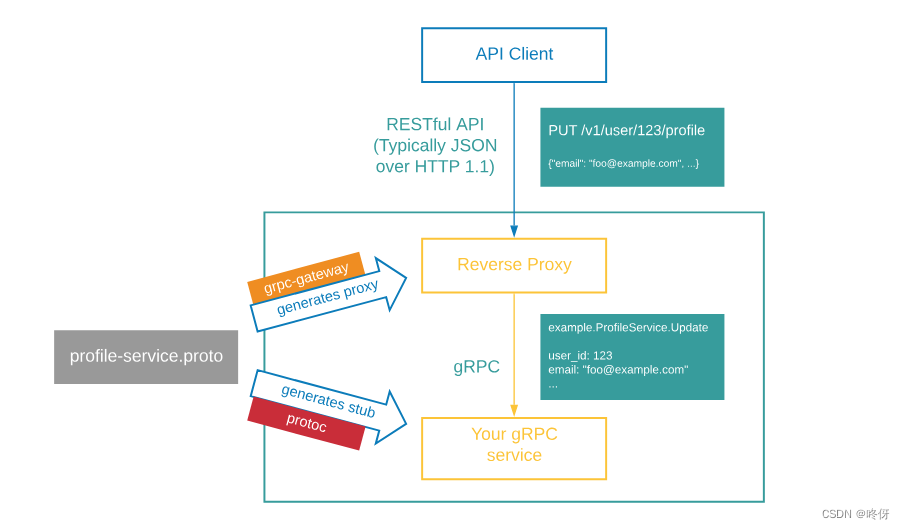
golang 工程组件:grpc-gateway 环境安装+默认网关测试
grpc-gateway grpc-gateway 顾名思义是专门是grpc的网关。也是一个protobuf的编译器,是一个proto的插件。 grpc-gateway就是将http请求处理后转发到对应grpc服务上。很多浏览器,或者客户端开箱不支持grpc,只支持传统的restful API。 grpc网关…...

IP地址SSL证书 IP证书
在许多企业用例中,公司需要SSL证书作为IP地址。公司使用IP地址通过Internet访问各种类型的应用程序。 公网IP地址的SSL证书: 内部IP(也称为私有IP)是IANA设置为保存的IPv4或IPv6地址,例如: RFC 1918范围内…...

MVCC 过程中会加锁吗?
MVCC 机制,全称(Multi-Version Concurrency Control)多版本并发控制,是确保 在高并发下, 多个事务读取数据时不加锁也可以多次读取相同的值。 MVCC 在读已提交(READ COMMITTED)、可重复读&…...
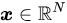
NLP入门——语言结构/语言建模
一、Linguistics 语言学 wordsmorphology 形态学:词的构成和内部结构研究。如英语的dog、dogs和dog-catcher有相当的关系morpheme 语素:最小的语法单位,是最小的音义结合体lexeme 词位:词的意义的基本抽象单位,是一组…...

2023java攻克了抖音视频去水印视频下载
2023java攻克了抖音视频去水印视频下载 1、过滤链接 /*** 过滤链接,获取http连接地址* param url* return*/public static String decodeHttpUrl(String url) {int start url.indexOf("http");int end url.lastIndexOf("/");String decodeu…...

云计算要学习哪些技术?
学习云计算需要涉及多个技术领域和相关的工具、平台和框架。以下是一个详细的介绍,帮助您了解学习云计算所需的技术。 1. 虚拟化技术 虚拟化是云计算的基础,因此了解虚拟化技术至关重要。学习虚拟化技术时,需要掌握以下知识点: …...

Spring bean 和 Java Bean的区别
Spring bean 和 Java Bean的区别 一,JavaBean JavaBean 是一种特殊的 Java 类,遵循一定的命名规范和属性访问规范。它是一种用于表示简单数据类型、封装业务逻辑或与其他对象交互的可重用组件。 JavaBean 必须满足以下规范: 公共无参构造方…...

性能测试 —— Jmeter 命令行详细
我们在启动Jmeter时 会看见:Don’t use GUI mode for load testing !, only for Test creation and Test debugging.For load testing, use CLI Mode (was NON GUI) 这句话的意思就是说,不要使用gui模式进行负载测试,gui模式仅仅是创建脚本…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

[QMT量化交易小白入门]-六十二、ETF轮动中简单的评分算法如何获取历史年化收益32.7%
本专栏主要是介绍QMT的基础用法,常见函数,写策略的方法,也会分享一些量化交易的思路,大概会写100篇左右。 QMT的相关资料较少,在使用过程中不断的摸索,遇到了一些问题,记录下来和大家一起沟通,共同进步。 文章目录 相关阅读1. 策略概述2. 趋势评分模块3 代码解析4 木头…...

Linux信号保存与处理机制详解
Linux信号的保存与处理涉及多个关键机制,以下是详细的总结: 1. 信号的保存 进程描述符(task_struct):每个进程的PCB中包含信号相关信息。 pending信号集:记录已到达但未处理的信号(未决信号&a…...
