分享 10 个高频 Python 面试题
Python 很容易学会,但很难掌握。
你可以在几天内了解它的基本语法,但是要能够用 Python 开发出足够好的商业软件,多年的实践是必须的。
因为,无论你使用哪种编程语言,你都必须对其复杂的内部机制有足够的了解,才能写出健壮的程序。
本文分享 10 个针对高级开发人员的 Python 面试题。它可以测试你对 Python 内部机制理解的程度。
一、Python中的整数缓存机制
面试官:
请解释在 Python shell 解释器上执行的代码的以下结果:
>>> a=256>>> b=256>>> a is bTrue>>> x=257>>> y=257>>> x is yFalse回答:
这是因为 Python 中的整数缓存机制。为了节省时间和内存成本,Python 总是预先加载 [-5, 256] 范围内的所有小整数。
因此,[-5, 256] 中的所有整数都已经保存在内存中。当声明此范围内的新整数变量时,Python 只是将缓存的整数引用到它,不会创建任何新对象。
因此,对结果的解释是:
当变量 a 和 b 分配给 256 时,它们被引用到存储 256 的相同内存位置。他们指向同一个对象。
当变量 a 和 b 被分配给 257 时,它们是不同内存位置的两个不同对象,因为 257 不在小整数缓存范围内。
由于 is 运算符要比较两个变量的内存位置,a is b 应该输出 True ,x is y 应该输出 False。
二、如何避免嵌套循环
面试官:
下面的程序使用了嵌套循环,你将如何优化它?
list_a = [1, 2020, 70]list_b = [2, 4, 7, 2000]list_c = [3, 70, 7]for a in list_a: for b in list_b: for c in list_c: if a + b + c == 2077: print(a, b, c)# 70 2000 7回答:
可以使用 itertools 中的 product 函数对其进行优化:
from itertools import productlist_a = [1, 2020, 70]list_b = [2, 4, 7, 2000]list_c = [3, 70, 7]for a, b, c in product(list_a, list_b, list_c): if a + b + c == 2077: print(a, b, c)# 70 2000 7因为 product 函数生成输入迭代的笛卡尔积。它可以帮助我们在很多场景中避免嵌套循环。
三、 类方法和静态方法
面试官:
在 Python 类中,类方法和静态方法有什么区别?
回答:
类方法是 Python 类中的第一个参数是类本身的方法。我们用 cls 这个参数来表示。
类方法不仅可以由实例调用,也可以由类直接调用。
静态方法是 Python 类中没有类或实例参数的方法。
因为静态方法不包含有关特定类或实例的参数。我们可以将其定义为类外的独立函数,并将其用作类外的其他普通函数。
可以阅读为什么 classmethod 比 staticmethod 更受宠?了解更多。
四、eval 函数的使用
面试官:
能否用一行 Python 代码中实现一个函数,它将接收两个数字 a 和 b 一个字符串 op。op 代表算术运算符,例如 “+”、“-”、“*”和“/” 。函数需要返回 op 的计算结果 a op b。
回答:
def cal(a, b, op): return eval(f'{a} {op} {b}')面试官:
好!那你能谈谈 eval 函数的缺点,以及为什么它不适合在生产中使用吗?
回答:
在生产环境中,我们应该仔细检查用户输入以避免意外问题。eval 函数会立即执行输入,这可能造成远程代码执行,这是非常危险的,强烈建议不要在生产环境使用 eval,即使你做了很多安全检查。可以阅读前文看完此文,你还会用 eval 吗?了解更多。
五、抽象类
面试官:
在面向对象编程中,有一个概念叫做抽象类。Python 也支持抽象类吗?
回答:
支持。Python 标准库有个模块 abc,它为抽象类提供功能。
通过继承类 abc.ABC,可以将类定义为抽象类,借助于装饰器 abc.abstractmethod,我们可以将方法定义为抽象方法。
例如:
from abc import ABC, abstractmethodclass Animal(ABC): @abstractmethod def move(self): pass六、函数传参的机制
面试官:
Python 是按值还是按引用传参?
回答:
既不是按值传递,也不是按引用传递,Python 自有一套机制,我们都知道 Python 的世界里,万物皆对象,从这个方面讲,传递给函数的,都是对象的地址,这有点像引用的概念,但是 Python 的对象分为可变对象和不可变对象,不可变对象就是不可修改的对象,例如:数字、字符串、元组,在不可变对象上的自增操作会新创建一个对象。
如果从其他编程语言过来学 Python 的,可以简单的这么理解:对于不可变对象,是按值传递,函数内部不会修改不可变对象,对于可变对象,是按引用(地址)传递,函数内部的修改会影响到参数本身。
可以阅读前文Python基础系列-可变/不可变数据类型了解更多。
七、Python 中的垃圾回收
面试官:
Python 如何收集垃圾(无用的对象)?
回答:
Python 使用一种称为引用计数的方法来决定何时需要在内存中收集对象。
简单来说,Python 会计算每个对象的引用计数,当一个对象没有引用时,会自动收集。
推荐这两篇文章来理解 Python 的垃圾回收:
学习一下 Python 的垃圾回收
Python 是如何管理内存的?
八、在 Python 函数中接收无限数量的参数
面试官:
请解释函数参数中星号的以下用法:
def func(*args, **kwargs): pass回答:
按照惯例,如果无法清楚地确定其参数的数量,我们会像示例一样定义一个 Python 函数。
以单个星号为前缀的参数 args 表示可以将任意数量的位置参数保存到元组中,args 就是这个元组的名称。
以两个星号为前缀的参数 kwargs 表示可以将任意数量的位置参数保存到字典中,kwargs 就是这个字典的名称。
九、 Lambda 函数
面试官:
Python 中的 lambda 函数是什么?你能否提供一个利用 lambda 函数强大功能的示例?
回答:
lambda 函数,或称为匿名函数,是一个没有函数名的简单 Python 函数。
编写 lambda 函数的模板是:
lambda 参数:表达式使用它的一个很好的场景是 sort 函数,比如:
leaders = ["Warren Buffett", "Yang Zhou", "Tim Cook", "Elon Musk"]print(leaders)# ['Warren Buffett', 'Yang Zhou', 'Tim Cook', 'Elon Musk']leaders.sort(key=lambda x: len(x))print(leaders)# ['Tim Cook', 'Yang Zhou', 'Elon Musk', 'Warren Buffett']十、Python 中的一些推导式
面试官:
Python中的推导式是什么?
回答:
推导式技巧是 Python 中的语法糖。它可以帮助轻松生成特定的数据结构。Python 中有四种类型的推导式:
列表推导式
生成器推导式
集合推导式
字典推导式
例如,我们可以如下生成字典:
Entrepreneurs = ["Yang", "Mark", "steve", "jack", "tom"]D1 = {id: name for id, name in enumerate(Entrepreneurs) if name[0].isupper()}print(D1)# {0: 'Yang', 1: 'Mark'}相关文章:

分享 10 个高频 Python 面试题
Python 很容易学会,但很难掌握。你可以在几天内了解它的基本语法,但是要能够用 Python 开发出足够好的商业软件,多年的实践是必须的。因为,无论你使用哪种编程语言,你都必须对其复杂的内部机制有足够的了解,…...
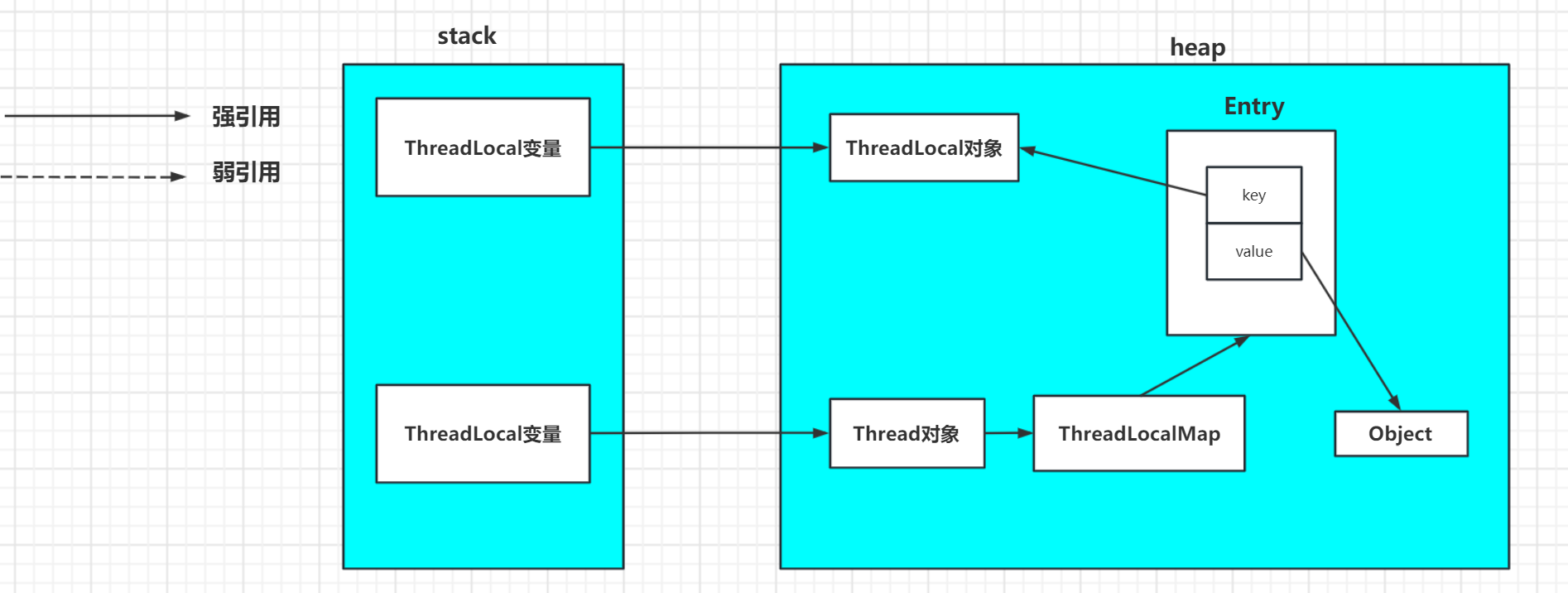
ThreadLocal原理、结构、源码解析
文章目录一、Thread简介1.什么是ThreadLocal2.为什么要是用ThreadLocal2.1Synchronized、Lock保证线程安全2.2ThreadLocal保证线程安全3.ThreadLocal和Synchronized的区别二、ThreadLocal原理1.Thread抽象内部结构2.ThreadLocal源码2.1Thread、ThreadLocal、ThreadLocalMap、En…...

分布式之PBFT算法
写在前面 在分布式之拜占庭问题 一文中我们分析了拜占庭问题,并一起看了支持拜占庭容错的口信消息性和签名消息性算法,但是这两种算法都有一个非常严重的问题,就是消息数量太多,通信的成本太大,消息数量复杂度为O(n ^…...
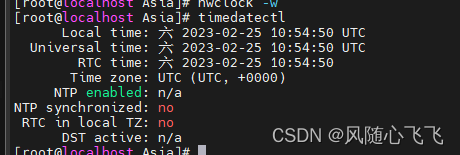
Linux 操作系统——查看/修改系统时区、时间、本地时间修改为UTC
文章目录1.背景描述2.知识储备3.解决步骤1. 查看当前时区2.修改设置Linux服务器时区3.复制相应的时区文件,替换系统时区文件;或者创建链接文件4. 查看和修改Linux的时间5. 硬件时间和系统时间的 相互同步1.背景描述 最近一个项目日期采用java8的LocalDa…...

CSS数据类型以及符号
css数据类型定义的是css属性中具有代表性的值,在规范的语法格式中,使用关键字外加一对 <和>表示,例如数值类型<number>、色值类型<color>等。 举个例子:background-image这个css属性语法结构如下: …...
LeetCode-54. 螺旋矩阵
题目来源 54. 螺旋矩阵 题目思路 while循环只遍历"环",不成环就不遍历了 四个边界 上边界 top : 0下边界 bottom : matrix.length - 1左边界 left : 0右边界 right : matrix[0].length - 1 矩阵不一定是方阵 top < bottom && left < r…...

【Python入门第十八天】Python For 循环
Python For 循环 for 循环用于迭代序列(即列表,元组,字典,集合或字符串)。 这与其他编程语言中的 for 关键字不太相似,而是更像其他面向对象编程语言中的迭代器方法。 通过使用 for 循环,我们…...

Qt图片定时滚动播放器
目录参考结构PicturePlay.promain.cpppictureplay.hpictureplay.cpppictureplay.ui效果源码参考 Qt图片浏览器 QT制作一个图片播放器 Qt中自适应的labelpixmap充满窗口后,无法缩小只能放大 可以显示jpg、jpeg、png、bmp。可以从电脑上拖动图到窗口并显示出来或者打开…...

李宏毅2023春季机器学习课程
目录2021&2022课程重磅须知我维护的其他项目更新日志课程地址课程资料直链课程作业直链其他优质课程2021&2022课程 CSDN Github 重磅须知 为方便所有网课资料与优质电子书籍的实时更新维护,创建一个在线实时网盘文件夹; 网盘获取方式&#…...

计算机操作系统知识点汇总
计算机操作系统选择填空题,300知识点,包含操作系统概论、处理机管理、内存管理、设备管理、文件管理等,为大学生期末创造奇迹提供无限可能 1、填空题 1、操作系统是对计算机资源进行管理的软件 2、操作系统是提供了处理机管理、 存储器管理…...

【离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表】
离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表一、DWD层设计要点二、交易域相关事实表1.交易域加购事务事实表1.加购事务事实表 前期梳理2.加购事务事实表 DDL表设计分析3.加购事务事实表 加载数据分析1.首日全…...
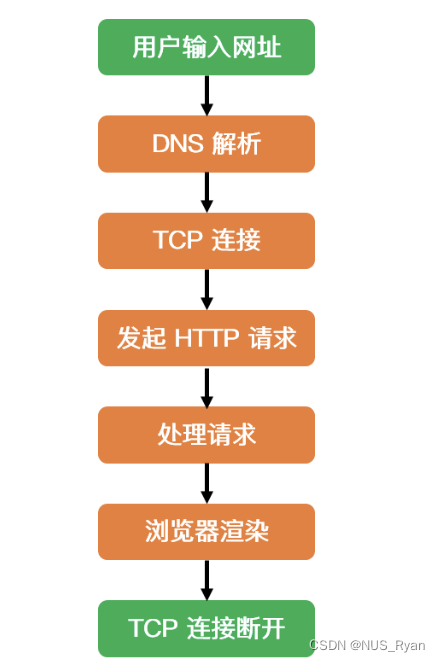
计算机网络(七):DNS协议和原理,DNS为什么用UDP,网页解析的全过程
文章目录一、什么是DNS二、DNS的作用三、DNS作用四、DNS为什么用UDP五、如果打开一个网站很慢,要如何排查六、网页解析的全过程一、什么是DNS DNS是域名系统的英文缩写,是一种组织成域层次结构的计算机和网络服务命名系统,用于TCP/IP网络。 …...
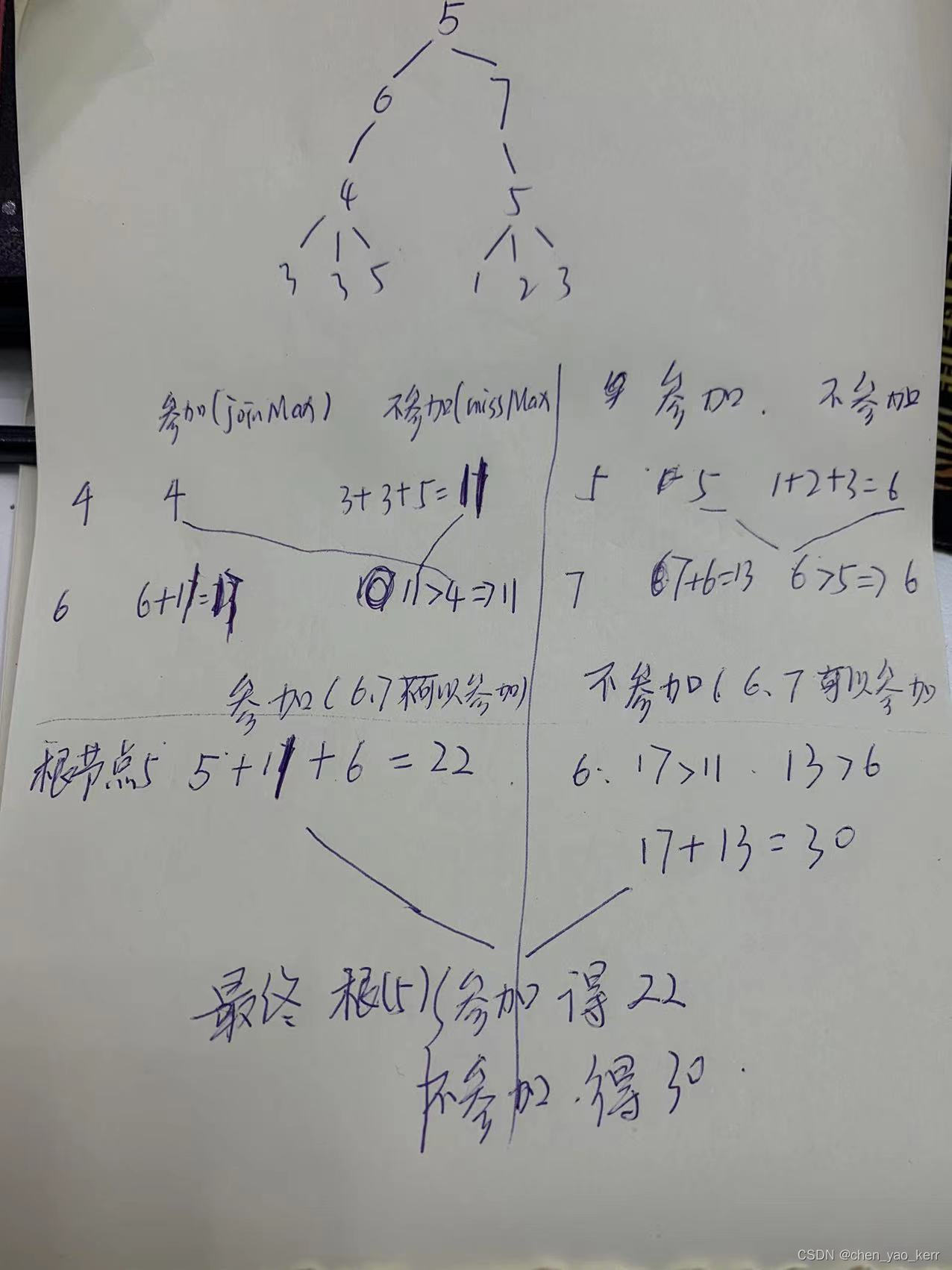
算法23:多叉树_派对的最大快乐值
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每…...

中国ETC行业市场规模及未来发展趋势
中国ETC行业市场规模及未来发展趋势编辑根据市场调研在线网发布的2023-2029年中国ETC行业发展策略分析及战略咨询研究报告分析:随着政府坚持实施绿色出行政策,ETC行业也受到了极大的支持。根据中国智能交通协会统计,2017年中国ETC行业市场规模…...
——只出现一次的数字)
每日刷题(一)——只出现一次的数字
前言 今天遇到一个位运算的题目,感觉很有意思,记录一下。 Question1 136. 只出现一次的数字 给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实…...
洛谷P5737 【深基7.例3】闰年展示 C语言/C++
【深基7.例3】闰年展示 题目描述 输入 x,yx,yx,y,输出 [x,y][x,y][x,y] 区间中闰年个数,并在下一行输出所有闰年年份数字,使用空格隔开。 输入格式 输入两个正整数 x,yx,yx,y,以空格隔开。 输出格式 第一行输出一个正整数&a…...

shell注释
注释对于任何编程语言都是不可忽视的重要组成部分,编写者通过注释来为其他人提供解释或提示,能有效提高代码的可读性。 Bash 同其他编程语言一样提供了两种类型注释的支持。 单行注释多行注释一、Bash 单行注释 在注释段落的开头使用 # ,如下…...
【C++入门(上篇)】C++入门学习
前言: 在之前的学习中,我们已经对初阶数据结构进行相应了学习,加上之前C语言的学习功底。今天,我们将会踏上更高一级“台阶”的学习-----即C的学习!!! 文章目录1.C 简介1.1什么是C1.2.C的发展史…...

【密码学】 一篇文章讲透数字签名
【密码学】 一篇文章讲透数字签名 数字签名介绍 数字签名(又称公钥数字签名)是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名…...

POI导入导出、EasyExcel批量导入和分页导出
文件导入导出POI、EasyExcel POI:消耗内存非常大,在线上发生过堆内存溢出OOM;在导出大数据量的记录的时候也会造成堆溢出甚至宕机,如果导入导出数据量小的话还是考虑的,下面简单介绍POI怎么使用 POI导入 首先拿到文…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
