【经典PageRank 】02/2 算法和线性代数

系列前文:【经典 PageRank 】01/2 PageRank的基本原理-CSDN博客
一、说明
并非所有连接都同样重要!
该算法由 Sergey 和 Lawrence 开发,用于在 Google 搜索中对网页进行排名。基本原则是重要或值得信赖的网页更有可能链接到其他重要网页。例如,来自信誉良好的网站的链接比来自不太知名的博客的链接具有更大的权重。
特征向量在理解 PageRank 算法的理论中发挥着基础作用。PageRank 和特征向量之间的联系可以在马尔可夫链或计算图及其稳态行为的背景下得到最好的理解。
二、特征向量和特征值
对于给定的方阵A和非零向量v,如果向量v满足方程A*v = λ*v ,则它是A的特征向量。这里,λ是称为特征值的标量,对应于特征向量v。从概念上讲,特征向量和特征向量是成对的值,其中特征向量在向量空间的某个基上具有向量变换的方向,特征值描述变换的大小。
2.1 网页排名
让我们将网络视为马尔可夫链,其中网页是节点或状态,页面之间的超链接作为方向边表示从一个页面转到另一页面的概率。当我们将此马尔可夫链表示为矩阵(称为转移矩阵)时,PageRank 算法的目标是找到一个稳态向量,其中概率总和为 1 或者没有进一步变化或收敛。查找页面排名的表达式由下式给出:
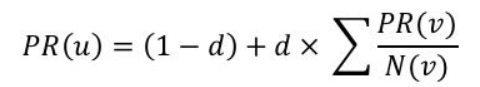
其中u:当前网页,d:阻尼因子,PR( v) :页面v的页面排名,N(v) :从v发出的链接数量
在 PageRank 的背景下,主导特征向量(对应于最大特征值的特征向量,在随机矩阵的情况下为 1)代表马尔可夫链的稳态分布。这种稳态分布就是我们试图计算的 PageRank 分数:系统中所有网页的概率分布,其中出现在页面上的概率不再随着进一步的转换而变化。
幂迭代方法涉及将向量(初始 PageRank 分数)重复乘以转移矩阵,本质上近似于该主特征向量。随着时间的推移,这个过程将会收敛,得到的向量将与矩阵的主特征向量成正比,从而给出网页的 PageRank 分数。
收敛背后的原因是,随着每次相乘(或转变),主要特征值的影响会增加,而其他特征值的影响会减小,特别是当引入阻尼因子时。最终,这导致向量与主特征向量成比例。
2.2 执行算法
- 将所有条目的页面排名得分矩阵初始化为 PR = 1/N。
- 表示网页- 如前所述,网络被想象为有向计算图。
- 阻尼因子- 引入来模拟随机网络冲浪者的行为,因为冲浪者大部分时间都会以概率d跟踪链接,但也会以(1-d)的概率移动到随机页面。
- 迭代- 使用上述表达式计算页面排名,直到它们收敛。
- 标准化- 经过几次迭代后,PageRank 值被标准化为总和为 1,以检查最大特征值 1。
def PageRank(transition_matrix, d, max_iterations, conv_thres):'''Arguments:transition_matrix: a matrix or numpy array representing the probabilities of going from one page to anotherd: damping factormax_iterations: number of iterationsconv_thres: convergence thresholdReturn: ranks of each webpage, as columns of the transition matrix'''#total number of web pagesN = transition_matrix.shape[0]#Intializing the transition matrix with equal probabilitiesPR = np.ones(N)/Nfor _ in range(max_iterations):PR_new = (1-d)/N + d*np.matmul(transition_matrix,PR)#normalizing the rank scoresPR_norm = np.linalg.norm(PR_new - PR, 1)#covergence constraintif PR_norm <= conv_thres:return PR_newPR = PR_newreturn PR 现在,让我们编写一个脚本,将转换矩阵可视化为马尔可夫链,其中网页作为状态或节点,超链接作为从一个页面移动到另一页面的概率。
def markov_chain(transition_matrix):# Create a directed graph.G = nx.DiGraph()# Nodes represent pages. Assume node labels are 0, 1, 2, ... for simplicity.num_nodes = transition_matrix.shape[0]G.add_nodes_from(range(num_nodes))# Iterate through the transition matrix to create edges.for i in range(num_nodes):for j in range(num_nodes):if transition_matrix[i, j] > 0: # Add edge if there's a non-zero transition probability.G.add_edge(i, j, weight=transition_matrix[i, j])# Visualize the graph.pos = nx.spring_layout(G)nx.draw_networkx_nodes(G, pos)nx.draw_networkx_labels(G, pos)nx.draw_networkx_edge_labels(G, pos, edge_labels={(u, v): f"{d['weight']:.2f}" for u, v, d in G.edges(data=True)})nx.draw_networkx_edges(G, pos)plt.title("Markov Chain from Transition Matrix")plt.axis("off")plt.show()三、实验代码
这是 GitHub 存储库链接:ashu1069/PageRank (github.com),由 python 脚本和 Jupyter Notebook 组成。该脚本包含使用自定义输入的驱动程序代码,其余部分在自述文件中进行了解释。
本质上,PageRank 值代表从网络链接结构导出的转换矩阵的主要特征向量。特征向量和特征值的数学为我们提供了计算这些值的理论基础和实用方法(幂迭代)。
import numpy as np
import networkx as nx
import matplotlib.pyplot as pltdef PageRank(transition_matrix, d, max_iterations, conv_thres):'''Arguments:transition_matrix: a matrix or numpy array representing the probabilities of going from one page to anotherd: damping factormax_iterations: number of iterationsconv_thres: convergence thresholdReturn: ranks of each webpage, as columns of the transition matrix'''#total number of web pagesN = transition_matrix.shape[0]#Intializing the transition matrix with equal probabilitiesPR = np.ones(N)/Nfor _ in range(max_iterations):PR_new = (1-d)/N + d*np.matmul(transition_matrix,PR)#normalizing the rank scoresPR_norm = np.linalg.norm(PR_new - PR, 1)#covergence constraintif PR_norm <= conv_thres:return PR_newPR = PR_newreturn PR def markov_chain(transition_matrix):# Create a directed graph.G = nx.DiGraph()# Nodes represent pages. Assume node labels are 0, 1, 2, ... for simplicity.num_nodes = transition_matrix.shape[0]G.add_nodes_from(range(num_nodes))# Iterate through the transition matrix to create edges.for i in range(num_nodes):for j in range(num_nodes):if transition_matrix[i, j] > 0: # Add edge if there's a non-zero transition probability.G.add_edge(i, j, weight=transition_matrix[i, j])# Visualize the graph.pos = nx.spring_layout(G)nx.draw_networkx_nodes(G, pos)nx.draw_networkx_labels(G, pos)nx.draw_networkx_edge_labels(G, pos, edge_labels={(u, v): f"{d['weight']:.2f}" for u, v, d in G.edges(data=True)})nx.draw_networkx_edges(G, pos)plt.title("Markov Chain from Transition Matrix")plt.axis("off")plt.show()if __name__ == '__main__':transition_matrix = np.array([[0.1,0.5,0.4],[0.2,0,0.2],[0,0.3,0.3]])d = 0.85max_iterations = 1000conv_thres = 1e-6PR = PageRank(transition_matrix, d, max_iterations, conv_thres)print(f'PageRanks:{PR}')markov_chain(transition_matrix)参考资料:
搜索引擎的剖析 (stanford.edu)
阿舒托什·库马尔
相关文章:
【经典PageRank 】02/2 算法和线性代数
系列前文:【经典 PageRank 】01/2 PageRank的基本原理-CSDN博客 一、说明 并非所有连接都同样重要! 该算法由 Sergey 和 Lawrence 开发,用于在 Google 搜索中对网页进行排名。基本原则是重要或值得信赖的网页更有可能链接到其他重要网页。例…...

【微客云】91优惠话费充值API接口开发功能介绍
话费充值接口文档 接口版本:1.0 ―、引言 文档概述 本文档提供话费充值接口规范说明,提供一整套的完整的接入示例(http 接口)供商户参 考,可以帮助商户开发人员快速完成接口开发与联调,实现与话费充值系统的交易互联。 公司官网…...

Kubernetes - 一键安装部署 K8S(附:Kubernetes Dashboard)
问题描述 不知道大伙是如何安装 K8s,特别还是集群的时候,我上一次安装搭建的时候,那个恶心到我了,真的是一步一个脚印走完整个搭建流程,爬了不少坑。 于是,才有了今天的文章,到底有没有可以一…...

Camera2开发基础知识篇——手机影像参数
1. 2、对焦 对焦指相机将图像清晰聚焦的过程。自动对焦功能可自动调整焦点,确保主体清晰锐利。手动对焦功能允许用户手动选择焦点。 3、焦距 简单理解就是指镜头的视角和放大倍数。实际到物理设备,焦距就是从镜片光学中心到底片、CCD或CMOS等成像平面…...

Unity之ShaderGraph如何实现无贴图水球效果
前言 我们今天来实现一个无贴图水球效果,如下图所示: 主要节点 UVSplit:可以获得UV在RGB三个颜色分别的分量 Remap:重映射节点 基于输入 In 值在输入In Min Max的 x 和 y 分量之间的线性插值,返回输入Out Min Max…...

【C语言】指针错题(类型分析)
题目: #include <stdio.h> int main () {int*p NULL;int arr[10] {0}; return 0; } 选项: A、p arr ; B、 int (* ptr )[10]& arr ; C、 p & arr [ 0 ]; D、 p & arr ; 解析: 1、 p 是一个指针变量,指…...
prosemirror 学习记录(二)创建 apple 节点
apple type 向 schema 中添加 apple type const nodes {apple: {inline: true,attrs: {name: { default: "unknown" },},group: "inline",draggable: true,parseDOM: [{tag: "span[custom-node-typeapple]",getAttrs(dom) {return {name: dom…...

自然语言处理---迁移学习
fasttext介绍 作为NLP工程领域常用的工具包,fasttext有两大作用:进行文本分类、训练词向量。在保持较高精度的情况下,快速的进行训练和预测是fasttext的最大优势。fasttext优势的原因: fasttext工具包中内含的fasttext模型具有十分简单的网络…...

node 第十天 原生node封装一个简易的服务器
原生node封装一个简易的服务器, 把前面几天的知识揉和起来做一个服务器基础实现, 首页访问, 静态资源服务器, 特定接口封装, 404app.js 服务器入口文件 app.js node app.js即可启动服务器 const { start } require(./modules/server); start();require_modules.js 整合模块导…...
intval函数的用法)
php实战案例记录(25)intval函数的用法
在PHP中,intval()函数用于将一个字符串转换为整数。它的语法如下: intval(string $value, int $base 10): int参数说明: $value:要转换的字符串。$base(可选):进制数,默认为10。如…...
laravel框架介绍(二) composer命令下载laravel报错
1.composer命令下载laravel报如下错 : curl error 18 while downloading https://repo.packagist.org/p2/symfony/uid.j son: transfer closed with 3808 bytes remaining to read,具体为 解决方案:执行以下命令切换镜像 >composer con…...

代码签名证书到期了怎么续费?
我们都知道代码签名证书最长期限可以申请3年,但有的首次申请也会申请1年,这种情况下证书到期了就意味着要重新办理,同样的实名验证步骤还需要再走一遍,尤其目前无论是哪种类型的代码签名证书都会有物理硬件,即使交钱实…...

JAVA 同城服务预约家政小程序开发的优势和运营
随着社会节奏的加快,人们对家庭清洁和维护的需求日益增长。为了满足这一需求,JAVA同城服务预约家政小程序应运而生。本文将详细介绍该小程序开发的优势及运营策略,帮助读者更好地了解其价值和潜力。 一、开发优势 方便快捷:用户…...

基于粒子群算法的无人机航迹规划-附代码
基于粒子群算法的无人机航迹规划 文章目录 基于粒子群算法的无人机航迹规划1.粒子群搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用粒子群算法来优化无人机航迹规划。 1.粒子群…...
前端使用qrcodejs2插件实现根据网址生成二维码
实现效果: 实现方法: 1.安装插件 npm install --save qrcodejs2 2.可以全局引入,也可以只在使用的vue文件中引入 import QRCode from qrcodejs2; 3.在vue文件的template中设置放置二维码的div <div id"qrcode"></di…...
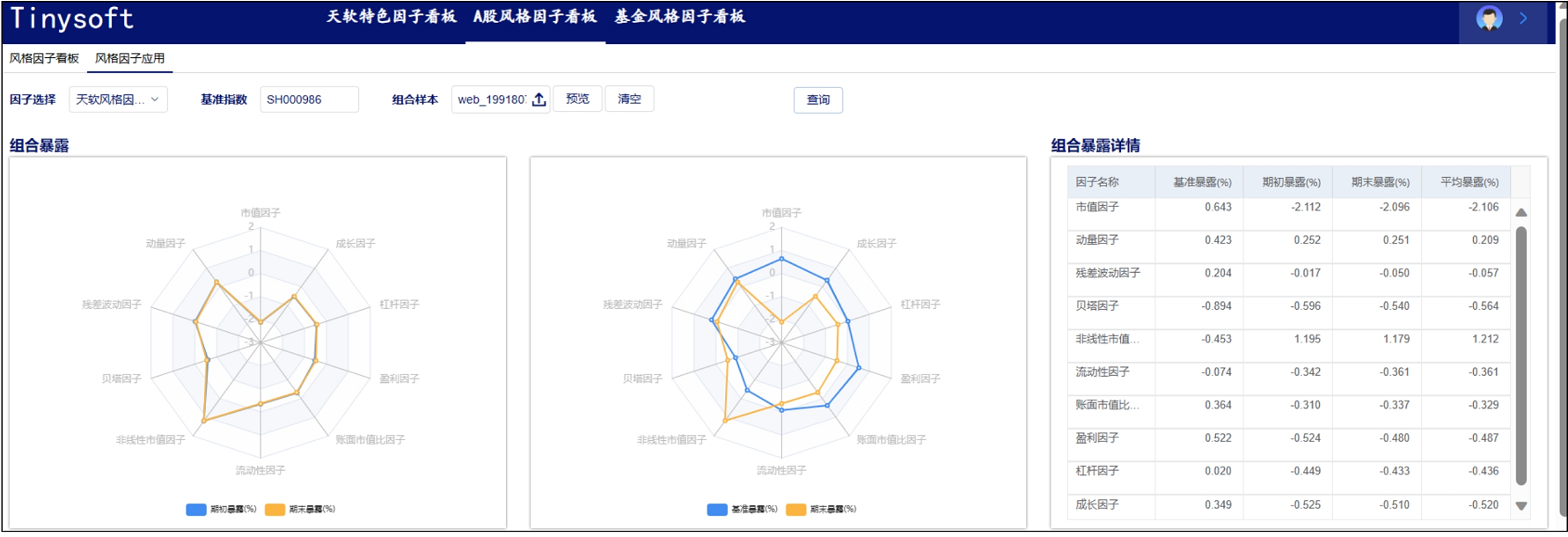
A股风格因子看板 (2023.10 第11期)
该因子看板跟踪A股风格因子,该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子,用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第11期,指数组合数据截止日2023-09-30,要点如下 近1年A股风格因子检验统…...

anaconda安装python 3.11
最近需要测试gpt researcher项目,gpt researcher项目的环境是3.11,于是用anaconda创建一个虚拟环境,结果报错了: UnsatisfiableError: The following specifications were found to be incompatible with each other:Package xz c…...

问题:EventSource 收不到流数据及 EventSource 的 onmessage 方法为null
文章目录 问题分析问题 在开发时,有用到 EventSource,但是在 new EventSource 的时候,打印 new EventSource 如下: onmessage : null, onerror : null, onopen: f(event)前端...

P2 B+树索引
文章目录 Task1 B树页B树页B树内部结点B树叶子结点 Task2 B树操作Task2 B树插入和搜索的单一值插入单一值搜索单一值 Task2 B树删除 Task3 叶子扫描的迭代器Task4 并行索引 Task1 B树页 B树页 实际上是每个B树页面的标题部分,包含叶子页面和内部页面共享的信息。 …...

爬虫知识之BeautifulSoup库安装及简单介绍
一. 前言 在前面的几篇文章中我介绍了如何通过Python分析源代码来爬取博客、维基百科InfoBox和图片,其文章链接如下: 其中核心代码如下: # coding=utf-8 import urllib import re #下载静态HTML网页 url=http://www.csdn.net/ content = urllib.urlopen(url).read…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
