当前位置： 首页 > news >正文

Unity之ShaderGraph如何实现无贴图水球效果

news 2026/2/8 15:25:01

前言

我们今天来实现一个无贴图水球效果，如下图所示：
在这里插入图片描述

主要节点

UV+Split：可以获得UV在RGB三个颜色分别的分量
在这里插入图片描述
Remap：重映射节点
基于输入 In 值在输入In Min Max的 x 和 y 分量之间的线性插值，返回输入Out Min Max的 x 和 y 分量之间的值。

Step：阶梯节点
如果输入In的值大于或等于输入Edge的值，则返回 1，否则返回 0。
在这里插入图片描述
Lerp：插值节点
返回输入T在输入A和输入B之间进行线性插值的结果。
例如，当输入T的值为0 时，返回值等于输入A的值，当输入 T 的值为 1 时，返回值等于输入B的值，当输入 T 的值为 0.5 时，返回值等于输入 B 的中点。两个输入A和B。
在这里插入图片描述
Ellipse：椭圆节点
根据输入UV生成椭圆形状，其大小由输入Width和Height指定。生成的形状可以通过连接平铺和偏移节点来偏移或平铺。
这里的椭圆目的是做一个椭圆的颜色提出，让上面的方形水波纹显示在一个球体内。
在这里插入图片描述

全部节点连线

在这里插入图片描述

相关文章：

Unity之ShaderGraph如何实现无贴图水球效果

前言 我们今天来实现一个无贴图水球效果，如下图所示： 主要节点 UVSplit：可以获得UV在RGB三个颜色分别的分量 Remap：重映射节点 基于输入 In 值在输入In Min Max的 x 和 y 分量之间的线性插值，返回输入Out Min Max…...

编程日记 2023/10/24 16:30:26

【C语言】指针错题（类型分析）

题目&#xff1a; #include <stdio.h> int main () {int*p NULL;int arr[10] {0}; return 0; } 选项&#xff1a; A、p arr ; B、 int (* ptr )[10]& arr ; C、 p & arr [ 0 ]; D、 p & arr ; 解析&#xff1a; 1、 p 是一个指针变量&#xff0c;指…...

编程日记 2023/10/24 16:29:25

prosemirror 学习记录（二）创建 apple 节点

apple type 向 schema 中添加 apple type const nodes {apple: {inline: true,attrs: {name: { default: "unknown" },},group: "inline",draggable: true,parseDOM: [{tag: "span[custom-node-typeapple]",getAttrs(dom) {return {name: dom…...

编程日记 2023/10/24 16:28:22

自然语言处理---迁移学习

fasttext介绍 作为NLP工程领域常用的工具包&#xff0c;fasttext有两大作用&#xff1a;进行文本分类、训练词向量。在保持较高精度的情况下&#xff0c;快速的进行训练和预测是fasttext的最大优势。fasttext优势的原因: fasttext工具包中内含的fasttext模型具有十分简单的网络…...

编程日记 2023/10/24 16:27:21

node 第十天 原生node封装一个简易的服务器

原生node封装一个简易的服务器, 把前面几天的知识揉和起来做一个服务器基础实现, 首页访问, 静态资源服务器, 特定接口封装, 404app.js 服务器入口文件 app.js node app.js即可启动服务器 const { start } require(./modules/server); start();require_modules.js 整合模块导…...

编程日记 2023/10/24 16:26:19

php实战案例记录(25)intval函数的用法

在PHP中&#xff0c;intval()函数用于将一个字符串转换为整数。它的语法如下&#xff1a; intval(string $value, int $base 10): int参数说明&#xff1a; $value&#xff1a;要转换的字符串。$base&#xff08;可选&#xff09;&#xff1a;进制数&#xff0c;默认为10。如…...

编程日记 2023/10/24 16:24:17

laravel框架介绍(二) composer命令下载laravel报错

1.composer命令下载laravel报如下错 &#xff1a; curl error 18 while downloading https://repo.packagist.org/p2/symfony/uid.j son: transfer closed with 3808 bytes remaining to read&#xff0c;具体为 解决方案&#xff1a;执行以下命令切换镜像 >composer con…...

编程日记 2023/10/24 16:23:16

代码签名证书到期了怎么续费？

我们都知道代码签名证书最长期限可以申请3年&#xff0c;但有的首次申请也会申请1年&#xff0c;这种情况下证书到期了就意味着要重新办理&#xff0c;同样的实名验证步骤还需要再走一遍&#xff0c;尤其目前无论是哪种类型的代码签名证书都会有物理硬件&#xff0c;即使交钱实…...

编程日记 2023/10/24 16:21:14

JAVA 同城服务预约家政小程序开发的优势和运营

随着社会节奏的加快&#xff0c;人们对家庭清洁和维护的需求日益增长。为了满足这一需求&#xff0c;JAVA同城服务预约家政小程序应运而生。本文将详细介绍该小程序开发的优势及运营策略&#xff0c;帮助读者更好地了解其价值和潜力。 一、开发优势 方便快捷&#xff1a;用户…...

编程日记 2023/10/24 16:20:13

基于粒子群算法的无人机航迹规划-附代码

基于粒子群算法的无人机航迹规划 文章目录 基于粒子群算法的无人机航迹规划1.粒子群搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要&#xff1a;本文主要介绍利用粒子群算法来优化无人机航迹规划。 1.粒子群…...

编程日记 2023/10/24 16:18:11

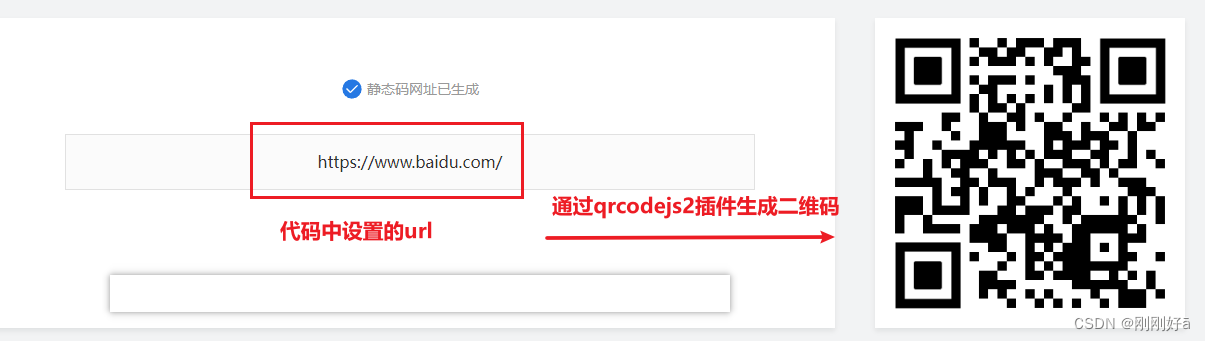
前端使用qrcodejs2插件实现根据网址生成二维码

实现效果&#xff1a; 实现方法&#xff1a; 1.安装插件 npm install --save qrcodejs2 2.可以全局引入&#xff0c;也可以只在使用的vue文件中引入 import QRCode from qrcodejs2; 3.在vue文件的template中设置放置二维码的div <div id"qrcode"></di…...

编程日记 2023/10/24 16:17:11

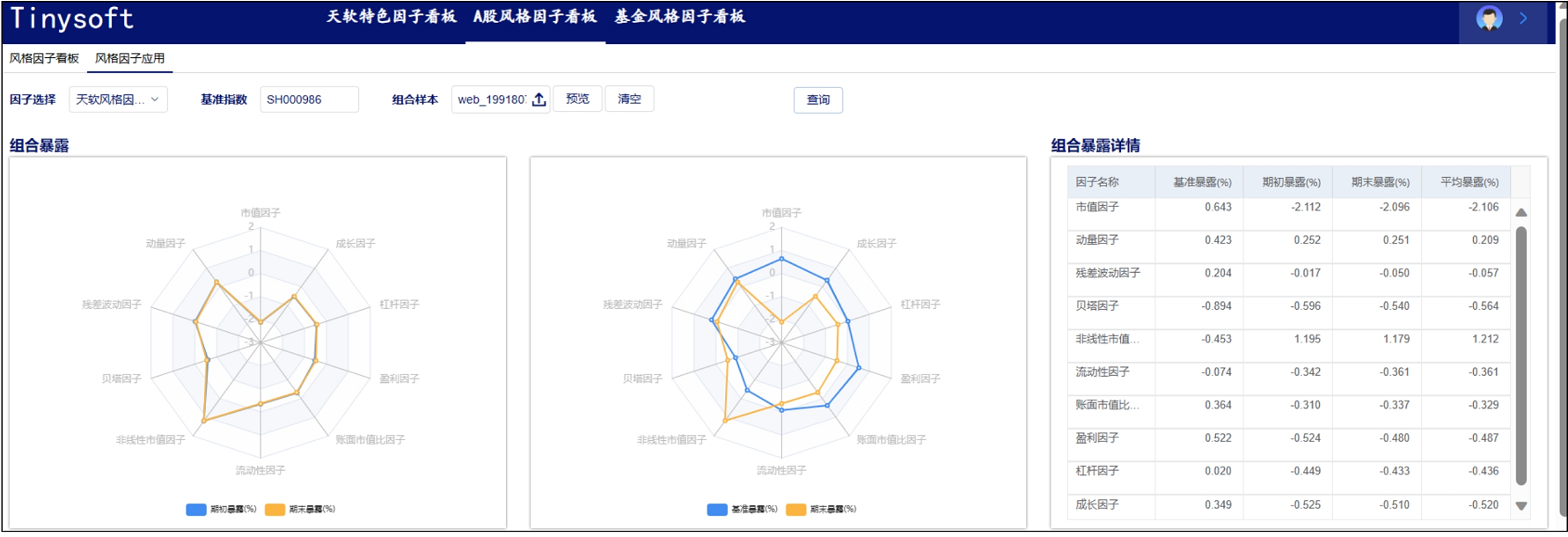
A股风格因子看板 (2023.10 第11期)

该因子看板跟踪A股风格因子&#xff0c;该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子&#xff0c;用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第11期&#xff0c;指数组合数据截止日2023-09-30&#xff0c;要点如下 近1年A股风格因子检验统…...

编程日记 2023/10/24 16:16:09

anaconda安装python 3.11

最近需要测试gpt researcher项目&#xff0c;gpt researcher项目的环境是3.11&#xff0c;于是用anaconda创建一个虚拟环境&#xff0c;结果报错了&#xff1a; UnsatisfiableError: The following specifications were found to be incompatible with each other:Package xz c…...

编程日记 2023/10/24 16:15:08

问题：EventSource 收不到流数据及 EventSource 的 onmessage 方法为null

文章目录 问题分析问题 在开发时，有用到 EventSource，但是在 new EventSource 的时候，打印 new EventSource 如下： onmessage : null, onerror : null, onopen: f(event)前端...

编程日记 2023/10/24 16:13:06

P2 B+树索引

文章目录 Task1 B树页B树页B树内部结点B树叶子结点 Task2 B树操作Task2 B树插入和搜索的单一值插入单一值搜索单一值 Task2 B树删除 Task3 叶子扫描的迭代器Task4 并行索引 Task1 B树页 B树页 实际上是每个B树页面的标题部分&#xff0c;包含叶子页面和内部页面共享的信息。 …...

编程日记 2023/10/24 16:12:05

爬虫知识之BeautifulSoup库安装及简单介绍

一. 前言 在前面的几篇文章中我介绍了如何通过Python分析源代码来爬取博客、维基百科InfoBox和图片，其文章链接如下： 其中核心代码如下： # coding=utf-8 import urllib import re #下载静态HTML网页 url=http://www.csdn.net/ content = urllib.urlopen(url).read…...

编程日记 2023/10/24 16:09:02

如何有效取代FTP来帮助企业快速传输大文件

在互联网的发展历史上&#xff0c;FTP是一种具有里程碑意义的协议&#xff0c;它最早出现在1971年&#xff0c;是实现网络上文件传输的基础。FTP的优点是简单、稳定、兼容性强&#xff0c;可以在不同的操作系统和平台之间进行文件交换。然而&#xff0c;时代在进步&#xff0c;…...

编程日记 2023/10/24 16:08:00

免登陆积分商城原理

有客户需要免登陆积分商城&#xff0c;研究了一下发现免登陆用途广泛&#xff0c;实现原理也很简单。如果是浏览器无非就是使用fingerprintjs2之类的扩展来实现获取浏览器指纹ID&#xff0c;如果是APP就获取设备唯一标识&#xff0c;然后在使用cryptojs加密来传递到php&#xf…...

编程日记 2023/10/24 16:07:00

muduo源码学习base——Atomic(原子操作与原子整数）

Atomic(原子操作与原子整数&#xff09; 前置知识AtomicIntegerTget()getAndAdd()getAndSet() 关于原子操作实现无锁队列(lock-free-queue) 前置知识 happens-before&#xff1a; 用来描述两个操作的内存可见性 如果操作 X happens-before 操作 Y&#xff0c;那么 X 的结果对于…...

编程日记 2023/10/24 16:05:56

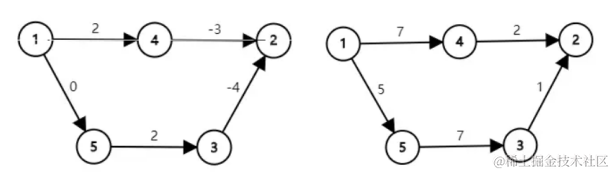
最短路相关笔记

Floyd Floyd 算法&#xff0c;是一种在图中求任意两点间最短路径的算法。 Floyd 算法适用于求解无负边权回路的图。 时间复杂度为 O ( n 3 ) O(n^3) O(n3)&#xff0c;空间复杂度 O ( n 2 ) O(n^2) O(n2)。 对于两点 ( i , j ) (i,j) (i,j) 之间的最短路径&#xff0c;有…...

编程日记 2023/10/24 16:04:55

conda相比python好处

Conda 作为 Python 的环境和包管理工具&#xff0c;相比原生 Python 生态&#xff08;如 pip 虚拟环境&#xff09;有许多独特优势&#xff0c;尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处&#xff1a; 一、一站式环境管理&#xff1a…...

编程新知 2025/11/29 6:54:19

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录

ASP.NET Core 是一个跨平台的开源框架&#xff0c;用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录&#xff0c;以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

编程新知 2026/2/8 4:37:06

【kafka】Golang实现分布式Masscan任务调度系统

要求&#xff1a; 输出两个程序&#xff0c;一个命令行程序&#xff08;命令行参数用flag&#xff09;和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽&#xff0c;然后将消息推送到kafka里面。 服务端程序&#xff1a; 从kafka消费者接收…...

编程新知 2026/2/4 19:38:41

以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：

一、属性动画概述NETX 作用&#xff1a;实现组件通用属性的渐变过渡效果&#xff0c;提升用户体验。支持属性&#xff1a;width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项&#xff1a; 布局类属性&#xff08;如宽高&#xff09;变化时&#…...

编程新知 2026/1/28 21:15:38

Day131 | 灵神 | 回溯算法 | 子集型 子集

Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣&#xff08;LeetCode&#xff09; 思路&#xff1a; 笔者写过很多次这道题了&#xff0c;不想写题解了&#xff0c;大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

编程新知 2026/1/23 12:37:51

如何在看板中体现优先级变化

在看板中有效体现优先级变化的关键措施包括&#xff1a;采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中&#xff0c;设置任务排序规则尤其重要&#xff0c;因为它让看板视觉上直观地体…...

编程新知 2026/1/23 12:42:28

大语言模型如何处理长文本？常用文本分割技术详解

为什么需要文本分割？ 引言：为什么需要文本分割？一、基础文本分割方法1. 按段落分割（Paragraph Splitting）2. 按句子分割（Sentence Splitting）二、高级文本分割策略3. 重叠分割（Sliding Window）4. 递归分割（Recursive Splitting）三、生产级工具推荐5. 使用LangChain的…...

编程新知 2025/11/18 0:32:13

376. Wiggle Subsequence

376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

编程新知 2026/2/8 10:51:38

工程地质软件市场：发展现状、趋势与策略建议

一、引言 在工程建设领域&#xff0c;准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具&#xff0c;正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

编程新知 2025/10/6 6:10:29

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/10/13 2:26:14